强化学习相关概念

马尔可夫决策过程

参考https://hrl.boyuai.com/chapter/1/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B/

简介

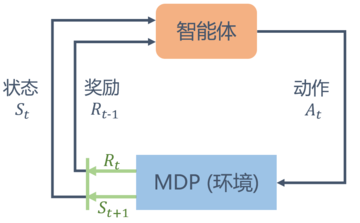
马尔可夫决策过程 （Markov decision process，MDP）包含状态信息以及状态之间的转移机制。

如果要用强化学习去解决一个实际问题，第一步要做的事情就是把这个实际问题抽象为一个马尔可夫决策过程，也就是明确马尔可夫决策过程的各个组成要素。本章将从马尔可夫过程出发，一步一步地进行介绍，最后引出马尔可夫决策过程。

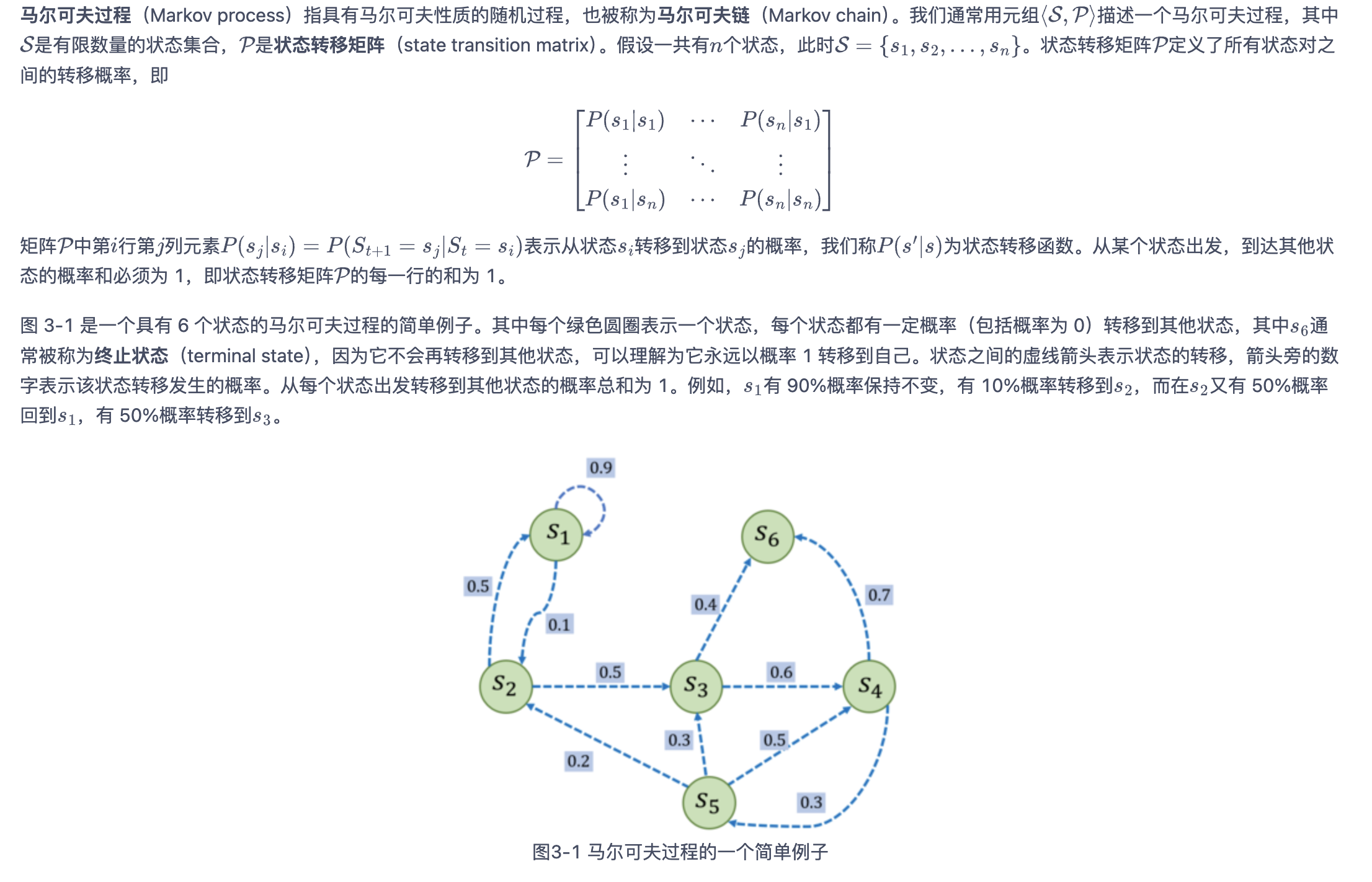
马尔可夫过程

随机过程

随机过程 （stochastic process）是概率论的“动力学”部分。概率论的研究对象是静态的随机现象，而随机过程的研究对象是随时间演变的随机现象（例如天气随时间的变化、城市交通随时间的变化）。

在随机过程中，随机现象在某时刻的取值是一个向量随机变量，用\(S_t\)表示，所有可能的状态组成状态集合\(S\)。随机现象便是状态的变化过程。在某时刻的状态\(S_t\)通常取决于时刻\(t\)之前的状态。我们将已知历史信息\((S_1,....,S_t)\)时下一个时刻状态为\(S_{t+1}\)的概率表示成\(P(S_{t+1}|S_1,....,S_t)\)。

马尔可夫性质

1723964194272

马尔可夫过程

1723964256002

1723964616071

马尔可夫奖励过程

1723964686115

回报

1723964752394

1723964852408

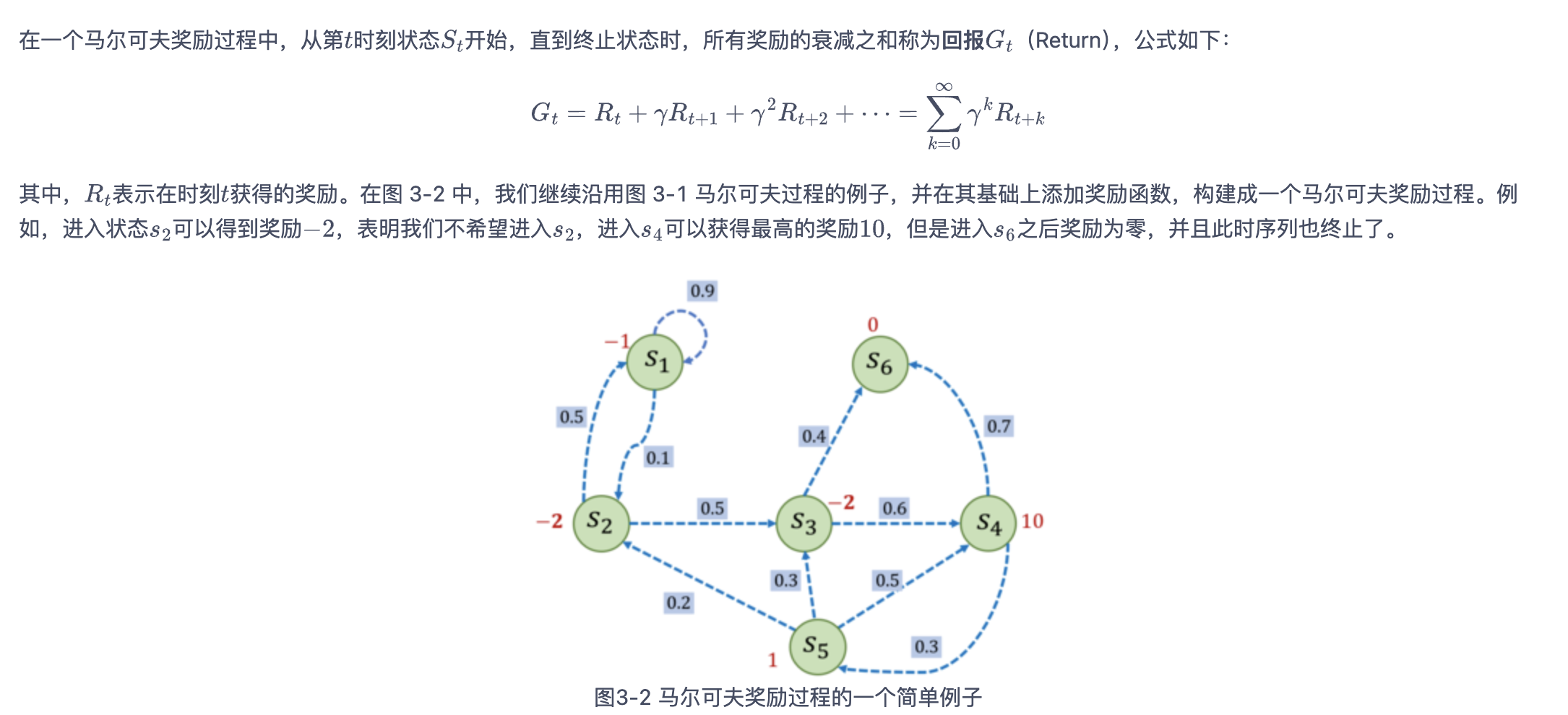
import numpy as np
np.random.seed(0)
# 定义状态转移概率矩阵P
P = [
    [0.9, 0.1, 0.0, 0.0, 0.0, 0.0],
    [0.5, 0.0, 0.5, 0.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.6, 0.0, 0.4],
    [0.0, 0.0, 0.0, 0.0, 0.3, 0.7],
    [0.0, 0.2, 0.3, 0.5, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.0, 0.0, 1.0],
]
P = np.array(P)

rewards = [-1, -2, -2, 10, 1, 0]  # 定义奖励函数
gamma = 0.5  # 定义折扣因子


# 给定一条序列,计算从某个索引（起始状态）开始到序列最后（终止状态）得到的回报
def compute_return(start_index, chain, gamma):
    G = 0
    for i in reversed(range(start_index, len(chain))):
        G = gamma * G + rewards[chain[i] - 1]
    return G


# 一个状态序列,s1-s2-s3-s6
chain = [1, 2, 3, 6]
start_index = 0
G = compute_return(start_index, chain, gamma)
print("根据本序列计算得到回报为：%s。" % G)

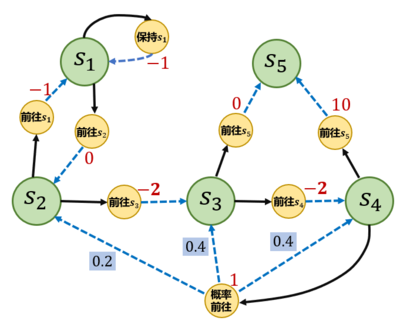
根据本序列计算得到回报为：-2.5。

价值函数

1723965101441

1724226890034

1724226911887

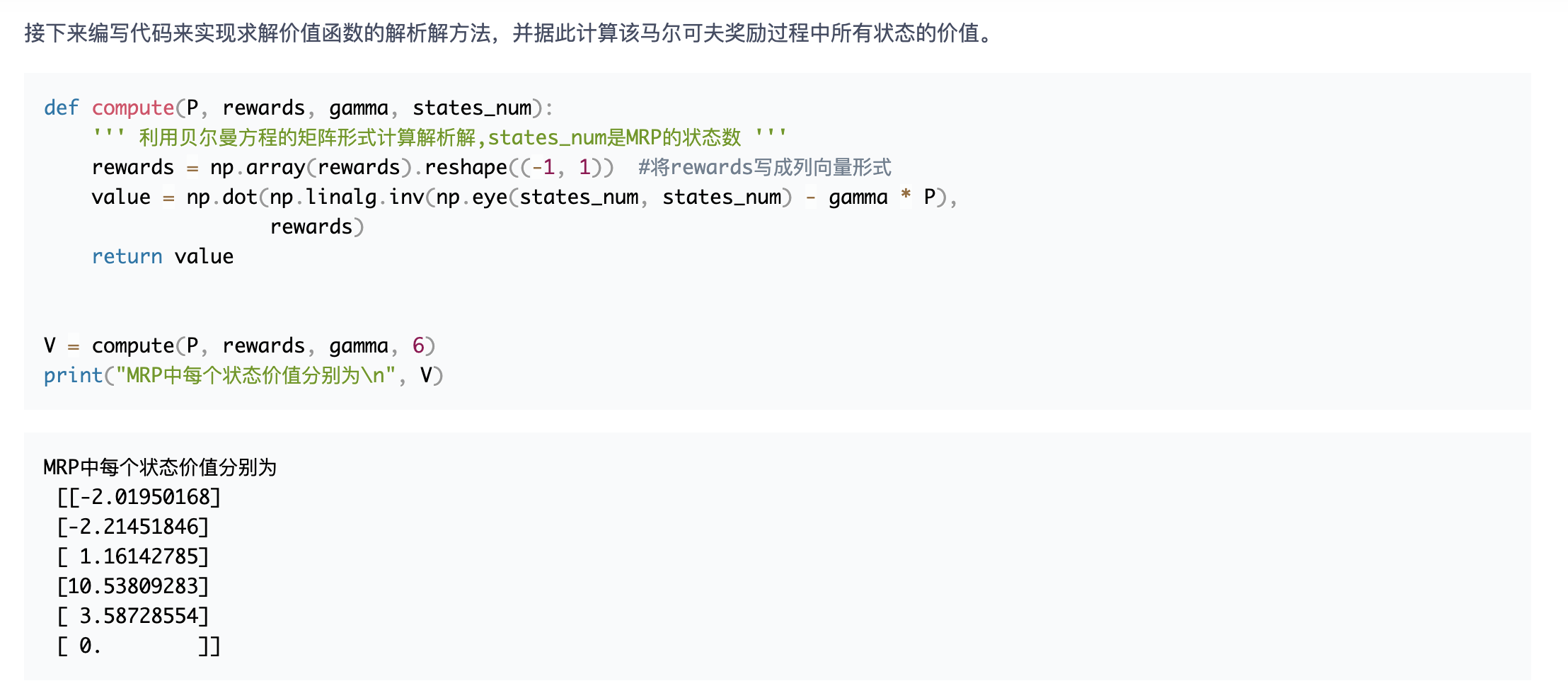
马尔可夫决策过程

在马尔可夫奖励过程（MRP）的基础上加入动作，就得到了马尔可夫决策过程（MDP）

我们发现 MDP 与 MRP 非常相像，主要区别为 MDP 中的状态转移函数和奖励函数都比 MRP 多了动作\(a\)作为自变量。

3.4.1 策略

1724227271129

3.4.2 状态价值函数

1724227494197

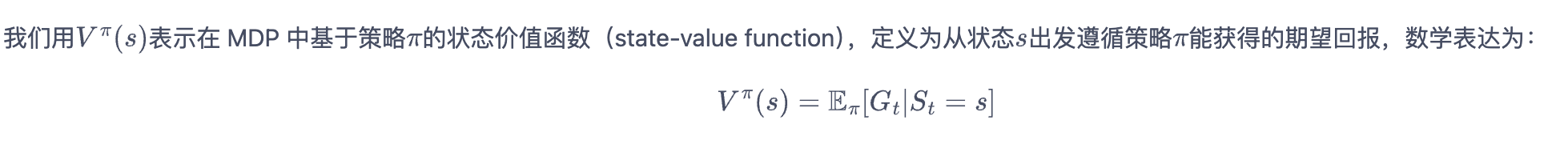
3.4.3 动作价值函数

1724227538558

3.4.4 贝尔曼期望方程

1724227691878

alt text

1724228028153

S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
# 状态转移函数
P = {
    "s1-保持s1-s1": 1.0,
    "s1-前往s2-s2": 1.0,
    "s2-前往s1-s1": 1.0,
    "s2-前往s3-s3": 1.0,
    "s3-前往s4-s4": 1.0,
    "s3-前往s5-s5": 1.0,
    "s4-前往s5-s5": 1.0,
    "s4-概率前往-s2": 0.2,
    "s4-概率前往-s3": 0.4,
    "s4-概率前往-s4": 0.4,
}
# 奖励函数
R = {
    "s1-保持s1": -1,
    "s1-前往s2": 0,
    "s2-前往s1": -1,
    "s2-前往s3": -2,
    "s3-前往s4": -2,
    "s3-前往s5": 0,
    "s4-前往s5": 10,
    "s4-概率前往": 1,
}
gamma = 0.5  # 折扣因子
MDP = (S, A, P, R, gamma)

# 策略1,随机策略
Pi_1 = {
    "s1-保持s1": 0.5,
    "s1-前往s2": 0.5,
    "s2-前往s1": 0.5,
    "s2-前往s3": 0.5,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.5,
    "s4-概率前往": 0.5,
}
# 策略2
Pi_2 = {
    "s1-保持s1": 0.6,
    "s1-前往s2": 0.4,
    "s2-前往s1": 0.3,
    "s2-前往s3": 0.7,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.1,
    "s4-概率前往": 0.9,
}


# 把输入的两个字符串通过“-”连接,便于使用上述定义的P、R变量
def join(str1, str2):
    return str1 + '-' + str2

1724228105447

1724228243011

1724228492907

这个 MRP 解析解的方法在状态动作集合比较大的时候不是很适用

3.5 蒙特卡洛方法

1724228630905

1724228662657

def sample(MDP, Pi, timestep_max, number):
    ''' 采样函数,策略Pi,限制最长时间步timestep_max,总共采样序列数number '''
    S, A, P, R, gamma = MDP
    episodes = []
    for _ in range(number):
        episode = []
        timestep = 0
        s = S[np.random.randint(4)]  # 随机选择一个除s5以外的状态s作为起点
        # 当前状态为终止状态或者时间步太长时,一次采样结束
        while s != "s5" and timestep <= timestep_max:
            timestep += 1
            rand, temp = np.random.rand(), 0
            # 在状态s下根据策略选择动作
            for a_opt in A:
                temp += Pi.get(join(s, a_opt), 0)
                if temp > rand:
                    a = a_opt
                    r = R.get(join(s, a), 0)
                    break
            rand, temp = np.random.rand(), 0
            # 根据状态转移概率得到下一个状态s_next
            for s_opt in S:
                temp += P.get(join(join(s, a), s_opt), 0)
                if temp > rand:
                    s_next = s_opt
                    break
            episode.append((s, a, r, s_next))  # 把（s,a,r,s_next）元组放入序列中
            s = s_next  # s_next变成当前状态,开始接下来的循环
        episodes.append(episode)
    return episodes


# 采样5次,每个序列最长不超过20步
episodes = sample(MDP, Pi_1, 20, 5)
print('第一条序列\n', episodes[0])
print('第二条序列\n', episodes[1])
print('第五条序列\n', episodes[4])

1724228707248

可以看到用蒙特卡洛方法估计得到的状态价值和我们用 MRP 解析解得到的状态价值是很接近的。这得益于我们采样了比较多的序列，感兴趣的读者可以尝试修改采样次数，然后观察蒙特卡洛方法的结果。

. . . . . . . . . 参考资料:https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/

DQN

DQN (Deep Q-Network)

简介

DQN 是一种将深度学习和 Q-Learning 结合起来的算法，由 Google DeepMind 团队提出。它利用深度神经网络来近似 Q 函数，从而处理高维度状态空间的问题。

算法流程

1. 经验回放（Experience Replay）：

   • 存储代理在环境中经历的转移 (state, action, reward, next state) 到一个回放记忆库中。
   • 在训练时，从记忆库中随机抽取小批量转移样本，用于更新 Q 网络，打破了样本之间的相关性，提高了训练稳定性。

2. 目标网络（Target Network）：

   • 除了主 Q 网络（online network），还引入了一个目标 Q 网络（target network）。
   • 主 Q 网络的参数每隔一定步数复制到目标 Q 网络，保持目标 Q 网络的参数固定一段时间，从而稳定训练过程。

3. 损失函数：

   • 

     1720883912505

主要优点

• 能处理高维度的状态空间。
• 通过经验回放和目标网络，解决了传统 Q-Learning 中的样本相关性和不稳定性问题。

Double Q-Learning

简介

Double Q-Learning 是一种改进的 Q-Learning 算法，旨在解决 Q-Learning 中存在的 过估计偏差 问题。过估计偏差是指 Q-Learning 在更新过程中倾向于高估 Q 值，这可能会导致次优策略的学习。

算法流程

1. 双 Q 网络：

   • 引入两个独立的 Q 网络 (Q_A) 和 (Q_B)，分别更新和选择动作。
   • 使用其中一个 Q 网络选择动作，另一个 Q 网络计算对应 Q 值。

2. 更新规则：

   • 选择动作时： [ a^* = _{a} Q_A(s', a) ]
   • 更新 Q 值时： [ Q_B(s, a) Q_B(s, a) + ( r + Q_A(s', a^*) - Q_B(s, a) ) ]
   • 每一步迭代中，使用 (Q_A) 和 (Q_B) 交替更新。

主要优点

• 减少了过估计偏差，提高了策略的稳定性和收敛性。
• 可以在不增加太多计算开销的情况下显著改善性能。

DQN 与 Double DQN 的结合

Double DQN（Double Deep Q-Network）结合了 DQN 和 Double Q-Learning 的优点，通过使用两个网络来分别选择动作和计算 Q 值，进一步减少了过估计偏差问题。

算法流程

1. 动作选择： [ a^* = {a} Q{}(s', a) ]
2. 目标 Q 值： [ y = r + Q_{}(s', a^*) ]
3. 损失函数： [ = ]

通过以上方法，Double DQN 在减少过估计偏差的同时，保持了 DQN 的高效性和稳定性。

总结

• DQN：结合深度学习和 Q-Learning，通过经验回放和目标网络解决样本相关性和不稳定性问题。
• Double Q-Learning：通过两个独立的 Q 网络减少过估计偏差，提高策略的稳定性。
• Double DQN：结合 DQN 和 Double Q-Learning 的优点，进一步减少过估计偏差，同时保持高效性和稳定性。

Policy Gradients

和以往的强化学习方法不同¶

1719547541292

强化学习是一个通过奖惩来学习正确行为的机制. 家族中有很多种不一样的成员, 有学习奖惩值, 根据自己认为的高价值选行为, 比如 Q learning, Deep Q Network, 也有不通过分析奖励值, 直接输出行为的方法, 这就是今天要说的 Policy Gradients 了. 甚至我们可以为 Policy Gradients 加上一个神经网络来输出预测的动作. 对比起以值为基础的方法, Policy Gradients 直接输出动作的最大好处就是, 它能在一个连续区间内挑选动作, 而基于值的, 比如 Q-learning, 它如果在无穷多的动作中计算价值, 从而选择行为, 这, 它可吃不消.

更新不同之处

1719547596446

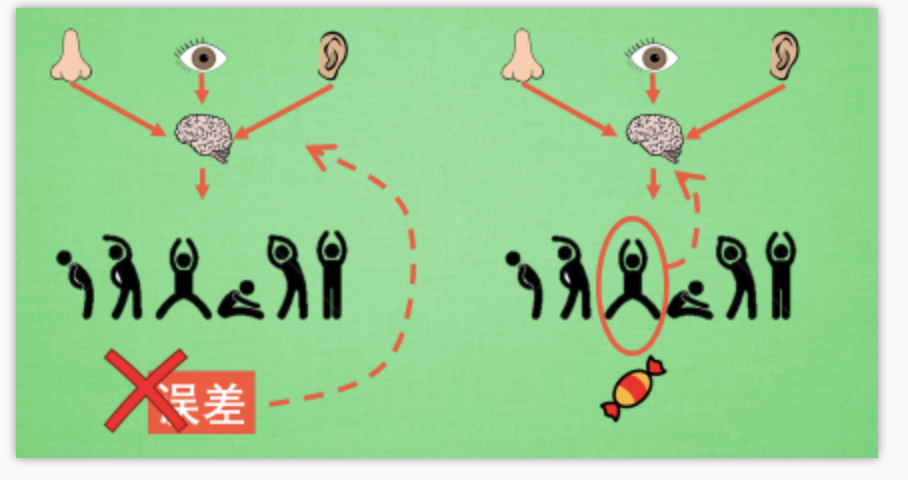
有了神经网络当然方便, 但是, 我们怎么进行神经网络的误差反向传递呢? Policy Gradients 的误差又是什么呢? 答案是! 哈哈, 没有误差! 但是他的确是在进行某一种的反向传递. 这种反向传递的目的是让这次被选中的行为更有可能在下次发生. 但是我们要怎么确定这个行为是不是应当被增加被选的概率呢? 这时候我们的老朋友, reward 奖惩正可以在这时候派上用场,

具体更新步骤

1719548100657

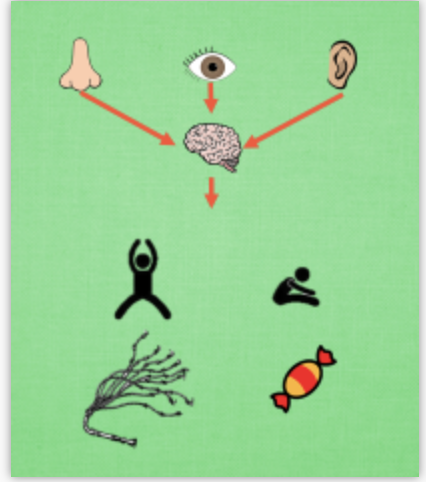
现在我们来演示一遍, 观测的信息通过神经网络分析, 选出了左边的行为, 我们直接进行反向传递, 使之下次被选的可能性增加, 但是奖惩信息却告诉我们, 这次的行为是不好的, 那我们的动作可能性增加的幅度 随之被减低. 这样就能靠奖励来左右我们的神经网络反向传递. 我们再来举个例子, 假如这次的观测信息让神经网络选择了右边的行为, 右边的行为随之想要进行反向传递, 使右边的行为下次被多选一点, 这时, 奖惩信息也来了, 告诉我们这是好行为, 那我们就在这次反向传递的时候加大力度, 让它下次被多选的幅度更猛烈! 这就是 Policy Gradients 的核心思想了. 很简单吧.

Policy gradient 是 RL 中另外一个大家族, 他不像 Value-based 方法 (Q learning, Sarsa), 但他也要接受环境信息 (observation), 不同的是他要输出不是 action 的 value, 而是具体的那一个 action, 这样 policy gradient 就跳过了 value 这个阶段. 而且个人认为 Policy gradient 最大的一个优势是: 输出的这个 action 可以是一个连续的值, 之前我们说到的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action. 而 policy gradient 可以在一个连续分布上选取 action.

算法¶

我们介绍的 policy gradient 的第一个算法是一种基于 整条回合数据 的更新, 也叫 REINFORCE 方法. 这种方法是 policy gradient 的最基本方法, 有了这个的基础, 我们再来做更高级的.

1719548643187

delta(log(Policy(s,a))*V) 表示在 状态 s 对所选动作 a 的吃惊度, 如果 Policy(s,a) (即在状态s下采取动作a的概率,上面的θ是整个神经网络的参数)概率越小, 反向的 log(Policy(s,a)) (即 -log(P)) 反而越大. 如果在 Policy(s,a) 很小的情况下, 拿到了一个 大的 R, 也就是 大的 V, 那 -delta(log(Policy(s, a))*V) 就更大, 表示更吃惊, (我选了一个不常选的动作, 却发现原来它能得到了一个好的 reward, 那我就得对我这次的参数进行一个大幅修改). 这就是吃惊度的物理意义啦.

建立 Policy 神经网络¶

这次我们要建立的神经网络是这样的: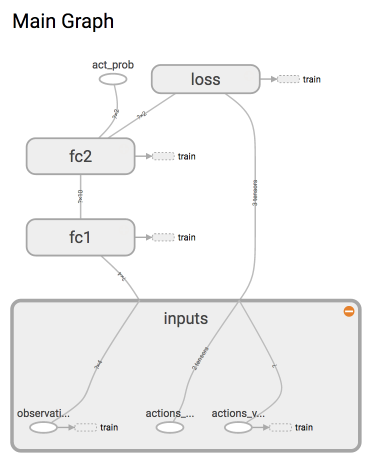

因为这是强化学习, 所以神经网络中并没有我们熟知的监督学习中的 y label. 取而代之的是我们选的 action.

class PolicyGradient:
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):
        ...
    def _build_net(self):
        with tf.name_scope('inputs'):
            self.tf_obs = tf.placeholder(tf.float32, [None, self.n_features], name="observations")  # 接收 observation
            self.tf_acts = tf.placeholder(tf.int32, [None, ], name="actions_num")   # 接收我们在这个回合中选过的 actions
            self.tf_vt = tf.placeholder(tf.float32, [None, ], name="actions_value") # 接收每个 state-action 所对应的 value (通过 reward 计算)

        # fc1
        layer = tf.layers.dense(
            inputs=self.tf_obs,
            units=10,   # 输出个数
            activation=tf.nn.tanh,  # 激励函数
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc1'
        )
        # fc2
        all_act = tf.layers.dense(
            inputs=layer,
            units=self.n_actions,   # 输出个数
            activation=None,    # 之后再加 Softmax
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc2'
        )

        self.all_act_prob = tf.nn.softmax(all_act, name='act_prob')  # 激励函数 softmax 出概率

        with tf.name_scope('loss'):
            # 最大化 总体 reward (log_p * R) 就是在最小化 -(log_p * R), 而 tf 的功能里只有最小化 loss
            neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts) # 所选 action 的概率 -log 值
            # 下面的方式是一样的:
            # neg_log_prob = tf.reduce_sum(-tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
            loss = tf.reduce_mean(neg_log_prob * self.tf_vt)  # (vt = 本reward + 衰减的未来reward) 引导参数的梯度下降

        with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)

这里有必要解释一下为什么我们使用的 loss= -log(prob)*vt 当做 loss, 因为下面有很多评论说这里不理解.

简单来说, 上面提到了两种形式来计算 neg_log_prob, 这两种形式是一模一样的, 只是第二个是第一个的展开形式.

如果你仔细看第一个形式, 这不就是在神经网络分类问题中的 cross-entropy 嘛! 使用 softmax 和神经网络的最后一层 logits 输出和真实标签 (self.tf_acts) 对比的误差. 并将神经网络的参数按照这个真实标签改进. 这显然和一个分类问题没有太多区别. 我们能将这个 neg_log_prob 理解成 cross-entropy 的分类误差.

分类问题中的标签是真实 x 对应的 y, 而我们 Policy gradient 中, x 是 state, y 就是它按照这个 x 所做的动作号码. 所以也可以理解成, 它按照 x 做的动作永远是对的 (出来的动作永远是正确标签), 它也永远会按照这个 正确标签 修改自己的参数. 可是事实却不是这样, 他的动作不一定都是 正确标签, 这就是强化学习(Policy gradient)和监督学习(classification)的不同.

Actor Critic

今天我们会来说说强化学习中的一种结合体 Actor Critic (演员评判家), 它合并了 以值为基础 (比如 Q learning) 和 以动作概率为基础 (比如 Policy Gradients) 两类强化学习算法.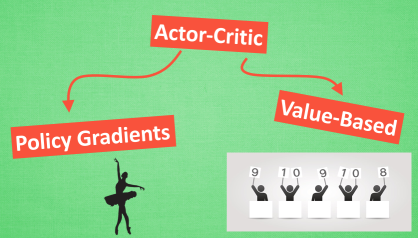

为什么要有 Actor 和 Critic

我们有了像 Q-learning 这么伟大的算法, 为什么还要瞎折腾出一个 Actor-Critic? 原来 Actor-Critic 的 Actor 的前生是 Policy Gradients, 这能让它毫不费力地在连续动作中选取合适的动作, 而 Q-learning 做这件事会瘫痪. 那为什么不直接用 Policy Gradients 呢? 原来 Actor Critic 中的 Critic 的前生是 Q-learning 或者其他的 以值为基础的学习法 , 能进行单步更新, 而传统的 Policy Gradients 则是回合更新, 这降低了学习效率.

Actor 和 Critic

alt text

现在我们有两套不同的体系, Actor 和 Critic, 他们都能用不同的神经网络来代替 . 在 Policy Gradients 的影片中提到过, 现实中的奖惩会左右 Actor 的更新情况. Policy Gradients 也是靠着这个来获取适宜的更新. 那么何时会有奖惩这种信息能不能被学习呢? 这看起来不就是 以值为基础的强化学习方法做过的事吗. 那我们就拿一个 Critic 去学习这些奖惩机制, 学习完了以后. 由 Actor 来指手画脚, 由 Critic 来告诉 Actor 你的那些指手画脚哪些指得好, 哪些指得差, Critic 通过学习环境和奖励之间的关系, 能看到现在所处状态的潜在奖励, 所以用它来指点 Actor 便能使 Actor 每一步都在更新, 如果使用单纯的 Policy Gradients, Actor 只能等到回合结束才能开始更新.

增加单步更新属性

alt text

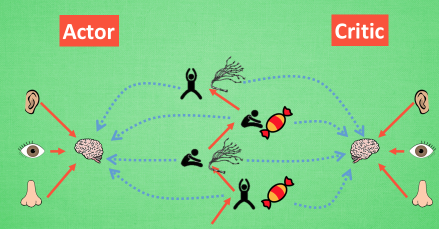
但是事物终有它坏的一面, Actor-Critic 涉及到了两个神经网络, 而且每次都是在连续状态中更新参数, 每次参数更新前后都存在相关性, 导致神经网络只能片面的看待问题, 甚至导致神经网络学不到东西. Google DeepMind 为了解决这个问题, 修改了 Actor Critic 的算法,

改进版 Deep Deterministic Policy Gradient (DDPG)

alt text

将之前在电动游戏 Atari 上获得成功的 DQN 网络加入进 Actor Critic 系统中, 这种新算法叫做 Deep Deterministic Policy Gradient, 成功的解决的在连续动作预测上的学不到东西问题. 所以之后, 我们再来说说什么是这种高级版本的 Deep Deterministic Policy Gradient 吧.

一句话概括 Actor Critic 方法 :

结合了 Policy Gradient (Actor) 和 Function Approximation (Critic) 的方法. Actor 基于概率选行为, Critic 基于 Actor 的行为评判行为的得分, Actor 根据 Critic 的评分修改选行为的概率.

Actor Critic 方法的优势 : 可以进行单步更新, 比传统的 Policy Gradient 要快.

Actor Critic 方法的劣势 : 取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛. 为了解决收敛问题, Google Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient. 后者融合了 DQN 的优势, 解决了收敛难的问题. 我们之后也会要讲到 Deep Deterministic Policy Gradient. 不过那个是要以 Actor Critic 为基础, 懂了 Actor Critic, 后面那个就好懂了.

算法

这套算法是在普通的 Policy gradient 算法上面修改的

Actor 修改行为时就像蒙着眼睛一直向前开车, Critic 就是那个扶方向盘改变 Actor 开车方向的.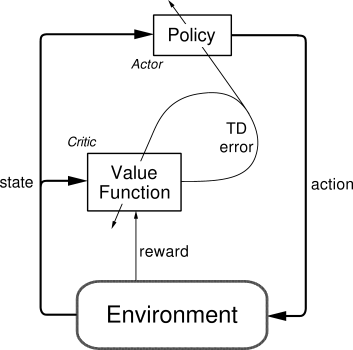

或者说详细点, 就是 Actor 在运用 Policy Gradient 的方法进行 Gradient ascent 的时候, 由 Critic 来告诉他, 这次的 Gradient ascent 是不是一次正确的 ascent, 如果这次的得分不好, 那么就不要 ascent 那么多.

代码主结构

alt text

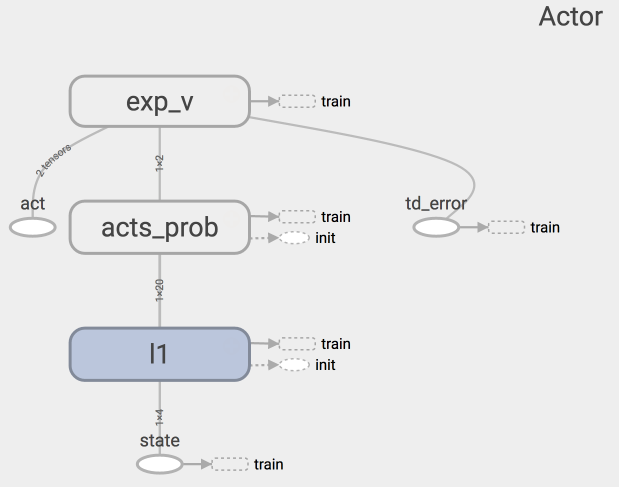
上图是 Actor 的神经网络结果, 代码结构在下面:

class Actor(object):
    def __init__(self, sess, n_features, n_actions, lr=0.001):
        # 用 tensorflow 建立 Actor 神经网络,
        # 搭建好训练的 Graph.

    def learn(self, s, a, td):
        # s, a 用于产生 Gradient ascent 的方向,
        # td 来自 Critic, 用于告诉 Actor 这方向对不对.

    def choose_action(self, s):
        # 根据 s 选 行为 a

alt text

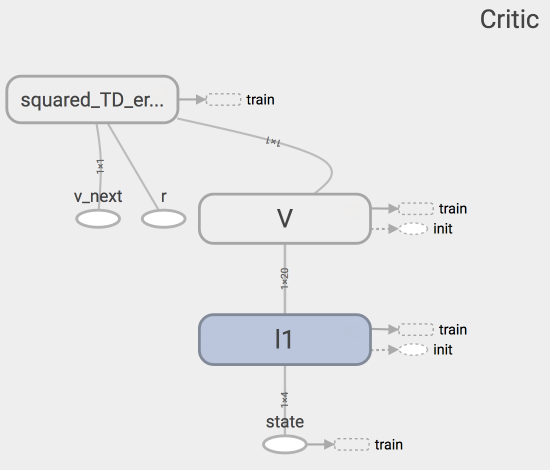
上图是 Critic 的神经网络结果, 代码结构在下面:

class Critic(object):
    def __init__(self, sess, n_features, lr=0.01):
        # 用 tensorflow 建立 Critic 神经网络,
        # 搭建好训练的 Graph.

    def learn(self, s, r, s_):
        # 学习 状态的价值 (state value), 不是行为的价值 (action value),
        # 计算 TD_error = (r + v_) - v,
        # 用 TD_error 评判这一步的行为有没有带来比平时更好的结果,
        # 可以把它看做 Advantage
        return # 学习时产生的 TD_error

两者学习方式

Actor 想要最大化期望的 reward, 在 Actor Critic 算法中, 我们用 比平时好多少 (TD error) 来当做 reward, 所以就是:

with tf.variable_scope('exp_v'):
    log_prob = tf.log(self.acts_prob[0, self.a])    # log 动作概率
    self.exp_v = tf.reduce_mean(log_prob * self.td_error)   # log 概率 * TD 方向
with tf.variable_scope('train'):
    # 因为我们想不断增加这个 exp_v (动作带来的额外价值),
    # 所以我们用过 minimize(-exp_v) 的方式达到
    # maximize(exp_v) 的目的
    self.train_op = tf.train.AdamOptimizer(lr).minimize(-self.exp_v)

Critic 的更新很简单, 就是像 Q learning 那样更新现实和估计的误差 (TD error) 就好了.

with tf.variable_scope('squared_TD_error'):
    self.td_error = self.r + GAMMA * self.v_ - self.v
    self.loss = tf.square(self.td_error)    # TD_error = (r+gamma*V_next) - V_eval
with tf.variable_scope('train'):
    self.train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)

每回合算法

for i_episode in range(MAX_EPISODE):
    s = env.reset()
    t = 0
    track_r = []    # 每回合的所有奖励
    while True:
        if RENDER: env.render()

        a = actor.choose_action(s)

        s_, r, done, info = env.step(a)

        if done: r = -20    # 回合结束的惩罚

        track_r.append(r)

        td_error = critic.learn(s, r, s_)  # Critic 学习
        actor.learn(s, a, td_error)     # Actor 学习

        s = s_
        t += 1

        if done or t >= MAX_EP_STEPS:
            # 回合结束, 打印回合累积奖励
            ep_rs_sum = sum(track_r)
            if 'running_reward' not in globals():
                running_reward = ep_rs_sum
            else:
                running_reward = running_reward * 0.95 + ep_rs_sum * 0.05
            if running_reward > DISPLAY_REWARD_THRESHOLD: RENDER = True  # rendering
            print("episode:", i_episode, "  reward:", int(running_reward))
            break

由于更新时的 网络相关性, state 相关性, Actor Critic 很难收敛

Deep Deterministic Policy Gradient (DDPG)

DDPG 最大的优势就是能够在连续动作上更有效地学习.

• 论文 Continuous control with deep reinforcement learning

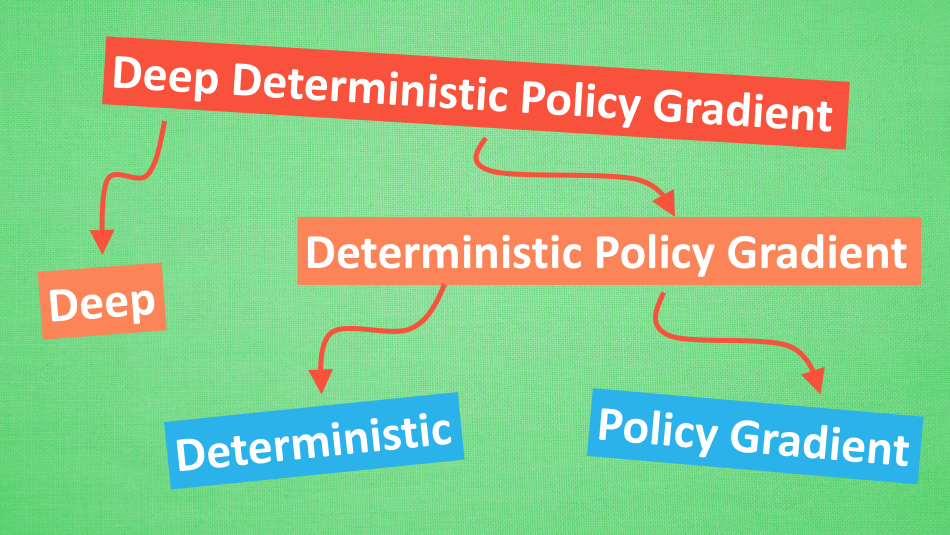
  它吸收了 Actor-Critic 让 Policy gradient 单步更新的精华, 而且还吸收让计算机学会玩游戏的 DQN 的精华, 合并成了一种新算法, 叫做 Deep Deterministic Policy Gradient. 那 DDPG 到底是什么样的算法呢, 我们就拆开来分析, 我们将 DDPG 分成 ‘Deep’ 和 ‘Deterministic Policy Gradient’, 然后 ‘Deterministic Policy Gradient’ 又能被细分为 ‘Deterministic’ 和 ‘Policy Gradient’, 接下来, 我们就开始一个个分析啦.

Deep 和 DQN

alt text

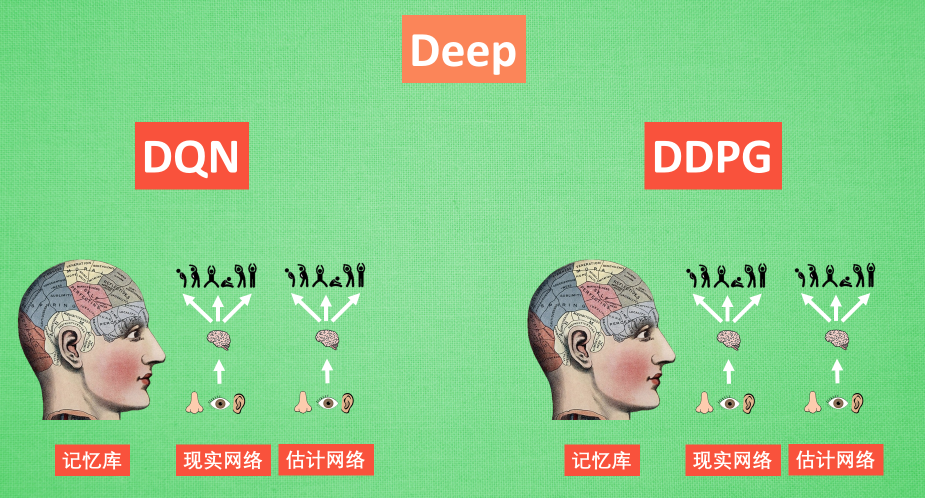
Deep 顾名思义, 就是走向更深层次, 我们在 DQN 的影片当中提到过, 使用一个记忆库和两套结构相同, 但参数更新频率不同的神经网络能有效促进学习. 那我们也把这种思想运用到 DDPG 当中, 使 DDPG 也具备这种优良形式. 但是 DDPG 的神经网络形式却比 DQN 的要复杂一点点

Deterministic Policy Gradient

alt text

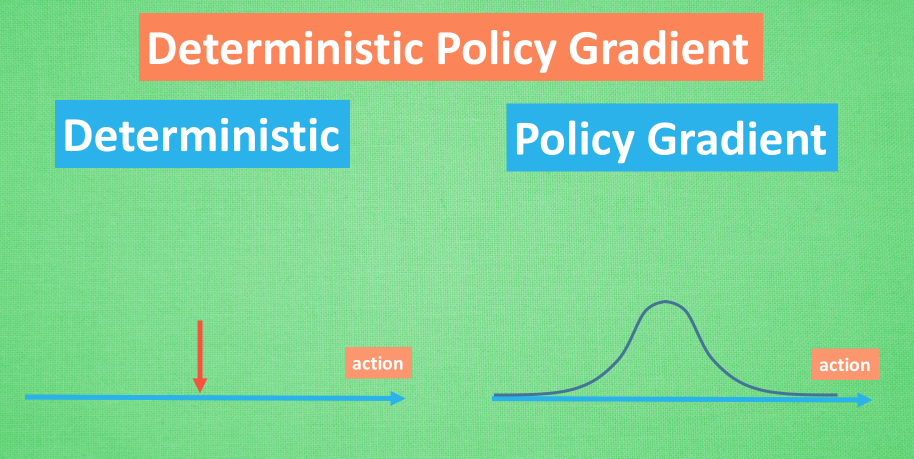
Policy gradient 我们也在之前的短片中提到过, 相比其他的强化学习方法, 它能被用来在连续动作上进行动作的筛选 . 而且筛选的时候是根据所学习到的动作分布随机进行筛选, 而 Deterministic 有点看不下去, Deterministic 说: 我说兄弟, 你其实在做动作的时候没必要那么不确定, 那么犹豫嘛, 反正你最终都只是要输出一个动作值, 干嘛要随机, 铁定一点, 有什么不好. 所以 Deterministic 就改变了输出动作的过程, 斩钉截铁的只在连续动作上输出一个动作值.

DDPG 神经网络

一句话概括 DDPG: Google DeepMind 提出的一种使用 Actor Critic 结构, 但是输出的不是行为的概率, 而是具体的行为, 用于连续动作 (continuous action) 的预测. DDPG 结合了之前获得成功的 DQN 结构, 提高了 Actor Critic 的稳定性和收敛性.

因为 DDPG 和 DQN 还有 Actor Critic 很相关, 所以最好这两者都了解下, 对于学习 DDPG 很有帮助. 我的教程链接都能在上面的学习资料中找到.

效果提前看:

alt text

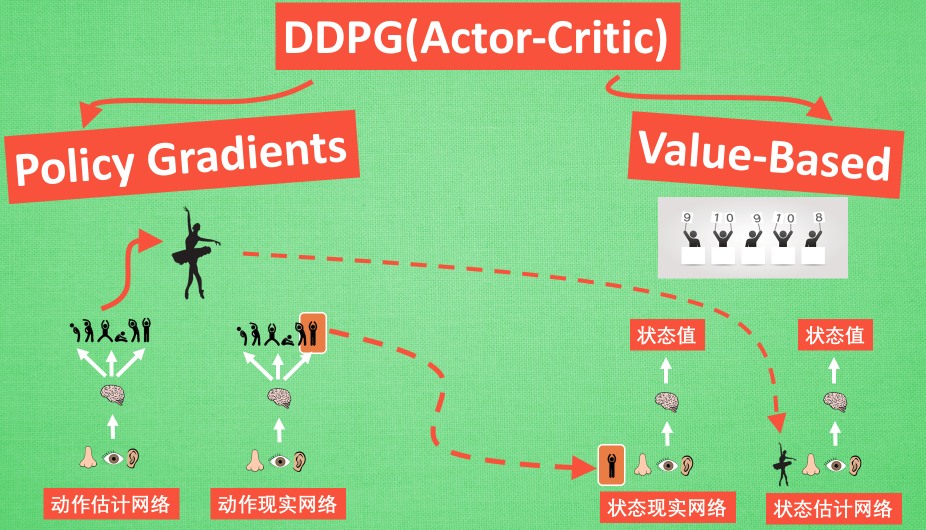
现在我们来说说 DDPG 中所用到的神经网络. 它其实和我们之前提到的 Actor-Critic 形式差不多, 也需要有基于 策略 Policy 的神经网络 和基于 价值 Value 的神经网络, 但是为了体现 DQN 的思想, 每种神经网络我们都需要再细分为两个, Policy Gradient 这边, 我们有估计网络和现实网络, 估计网络用来输出实时的动作, 供 actor 在现实中实行. 而现实网络则是用来更新价值网络系统的. 所以我们再来看看价值系统这边, 我们也有现实网络和估计网络, 他们都在输出这个状态的价值, 而输入端却有不同, 状态现实网络这边会拿着从动作现实网络来的动作加上状态的观测值加以分析, 而状态估计网络则是拿着当时 Actor 施加的动作当做输入.在实际运用中, DDPG 的这种做法的确带来了更有效的学习过程.

算法

DDPG 的算法实际上就是一种 Actor Critic

关于 Actor 部分

1720883530165

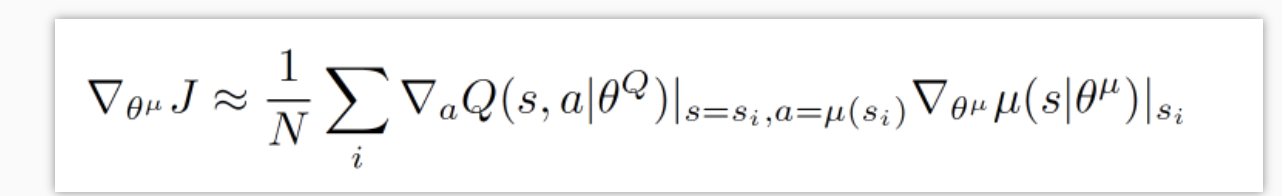
关于 Actor 部分, 他的参数更新同样会涉及到 Critic, 上面是关于 Actor 参数的更新, 它的前半部分 grad[Q] 是从 Critic 来的, 这是在说: 这次 Actor 的动作要怎么移动, 才能获得更大的 Q , 而后半部分 grad[u] 是从 Actor 来的, 这是在说: Actor 要怎么样修改自身参数, 使得 Actor 更有可能做这个动作 . 所以两者合起来就是在说: Actor 要朝着更有可能获取大 Q 的方向修改动作参数了 .

注:

其中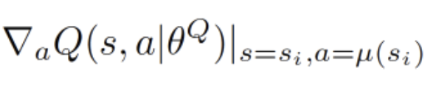就是下图中的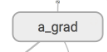

关于 Critic 的更新

1720883686080

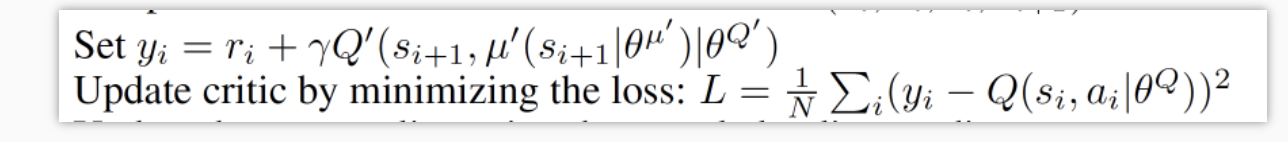
上面这个是关于 Critic 的更新, 它借鉴了 DQN 和 Double Q learning 的方式, 有两个计算 Q 的神经网络, Q_target 中依据下一状态, 用 Actor 来选择动作, 而这时的 Actor 也是一个 Actor_target (有着 Actor 很久之前的参数). 使用这种方法获得的 Q_target 能像 DQN 那样切断相关性, 提高收敛性.

主结构

我们用 Tensorflow 搭建神经网络, 主结构可以见这个 tensorboard 的出来的图.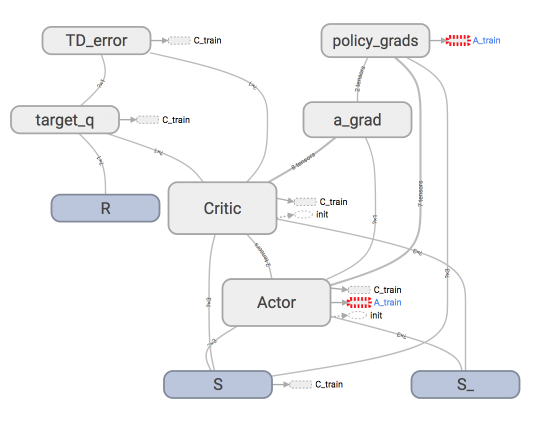

看起来很复杂吧, 没关系, 我们一步步来, 拆开来看就容易了. 首先看看 Actor 和 Critic 中各有什么结构.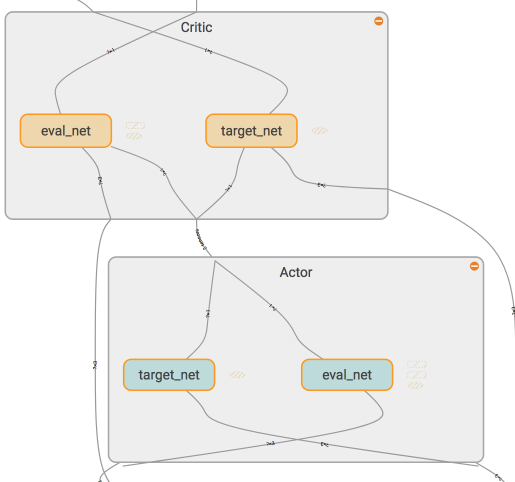

class Actor(object):
    def __init__(self):
        ...
        with tf.variable_scope('Actor'):
            # 这个网络用于及时更新参数
            self.a = self._build_net(S, scope='eval_net', trainable=True)
            # 这个网络不及时更新参数, 用于预测 Critic 的 Q_target 中的 action
            self.a_ = self._build_net(S_, scope='target_net', trainable=False)
        ...

class Critic(object):
    def __init__(self):
        with tf.variable_scope('Critic'):
            # 这个网络是用于及时更新参数
            self.a = a  # 这个 a 是来自 Actor 的, 但是 self.a 在更新 Critic 的时候是之前选择的 a 而不是来自 Actor 的 a.
            self.q = self._build_net(S, self.a, 'eval_net', trainable=True)
            # 这个网络不及时更新参数, 用于给出 Actor 更新参数时的 Gradient ascent 强度
            self.q_ = self._build_net(S_, a_, 'target_net', trainable=False)

Actor Critic

有了对 Actor Critic 每个里面各两个神经网络结构的了解, 我们再来具体看看他们是如何进行交流, 传递信息的. 我们从 Actor 的学习更新方式开始说起.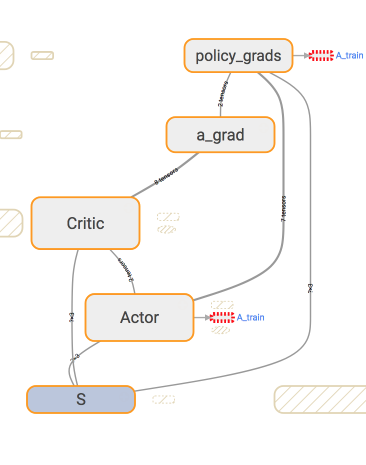

这张图我们就能一眼看穿 Actor 的更新到底基于了哪些东西. 可以看出, 它使用了两个 eval_net, 所以 Actor class 中用于 train 的代码我们这样写:

with tf.variable_scope('policy_grads'):
    # 这是在计算 (dQ/da) * (da/dparams)
    self.policy_grads = tf.gradients(
        ys=self.a, xs=self.e_params, # 计算 ys 对于 xs 的梯度
        grad_ys=a_grads # 这是从 Critic 来的 dQ/da
    )
with tf.variable_scope('A_train'):
    opt = tf.train.AdamOptimizer(-self.lr)  # 负的学习率为了使我们计算的梯度往上升, 和 Policy Gradient 中的方式一个性质
    self.train_op = opt.apply_gradients(zip(self.policy_grads, self.e_params)) # 对 eval_net 的参数更新

同时下面也提到的传送给 Actor 的 a_grad 应该用 Tensorflow 怎么计算. 这个 a_grad 是 Critic class 里面的, 这个 a 是来自 Actor 根据 S 计算而来的:

with tf.variable_scope('a_grad'):
    self.a_grads = tf.gradients(self.q, self.a)[0]   # dQ/da

而在 Critic 中, 我们用的东西简单一点.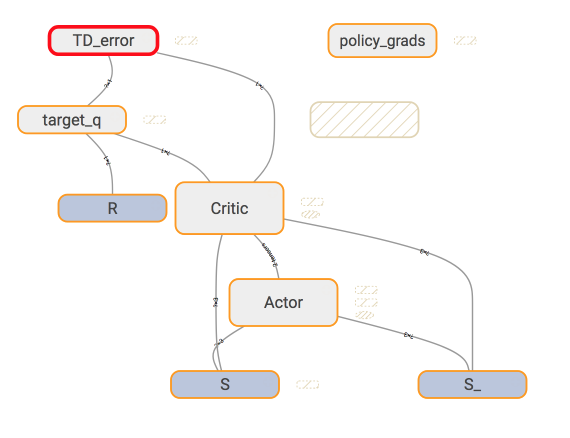

下面就是 Critic 更新时的代码了.

# 计算 target Q
with tf.variable_scope('target_q'):
    self.target_q = R + self.gamma * self.q_    # self.q_ 根据 Actor 的 target_net 来的
# 计算误差并反向传递误差
with tf.variable_scope('TD_error'):
    self.loss = tf.reduce_mean(tf.squared_difference(self.target_q, self.q))  # self.q 又基于 Actor 的 target_net
with tf.variable_scope('C_train'):
    self.train_op = tf.train.AdamOptimizer(self.lr).minimize(self.loss)

最后我们建立并把 Actor 和 Critic 融合在一起的时候是这样写的.

actor = Actor(...)
critic = Critic(..., actor.a, actor.a_)  # 将 actor 同它的 eval_net/target_net 产生的 a/a_ 传给 Critic
actor.add_grad_to_graph(critic.a_grads) # 将 critic 产出的 dQ/da 加入到 Actor 的 Graph 中去

记忆库 Memory

以下是关于类似于 DQN 中的记忆库代码, 我们用一个 class 来建立

class Memory(object):
    def __init__(self, capacity, dims):
        """用 numpy 初始化记忆库"""

    def store_transition(self, s, a, r, s_):
        """保存每次记忆在 numpy array 里"""

    def sample(self, n):
        """随即从记忆库中抽取 n 个记忆进行学习"""

每回合算法

var = 3  # 这里初始化一个方差用于增强 actor 的探索性

for i in range(MAX_EPISODES):
    ...
    for j in range(MAX_EP_STEPS):
        ...

        a = actor.choose_action(s)
        a = np.clip(np.random.normal(a, var), -2, 2) # 增强探索性
        s_, r, done, info = env.step(a)

        M.store_transition(s, a, r / 10, s_)   # 记忆库

        if M.pointer > MEMORY_CAPACITY: # 记忆库头一次满了以后
            var *= .9998    # 逐渐降低探索性
            b_M = M.sample(BATCH_SIZE)
            ...   # 将 b_M 拆分成下面的输入信息
            critic.learn(b_s, b_a, b_r, b_s_)
            actor.learn(b_s)

        s = s_

        if j == MAX_EP_STEPS-1:
            break

我也用这套 DDPG 测试过自己写的机器手臂的环境, 发现效果也还行. 有兴趣的朋友可以看到这里.

有很多人留言说想要我做一个关于这个机器手臂的教程, 不负众望, 你可以在这里 看到我怎么从零开始, 手写环境, debug 测试, 来制作一个强化学习的机器手臂.

Asynchronous Advantage Actor-Critic (A3C)

强化学习中的一种有效利用计算资源, 并且能提升训练效用的算法, Asynchronous Advantage Actor-Critic, 简称 A3C.

平行宇宙

alt text

我们先说说没什么关系的,大家知道平行宇宙这回事. 想像现在有三个平行宇宙, 那么就意味着这3个平行宇宙上存在3个你, 而你可能在电脑前呆了很久, 对, 说的就是你! 然后你会被我催促起来做运动~ 接着你 和 你 还有 你, 就无奈地在做着不同的运动, 油~ 我才不想知道你在做什么样的运动呢. 不过这3个你 都开始活动胫骨啦. 假设3个你都能互相通信, 告诉对方, “我这个动作可以有效缓解我的颈椎病”, “我做那个动作后, 腰就不痛了 “, “我活动了手臂, 肩膀就不痛了”. 这样你是不是就同时学到了对身体好的三招. 这样是不是感觉特别有效率. 让你看看更有效率的, 那就想想3个你同时在写作业, 一共3题, 每人做一题, 只用了1/3 的时间就把作业做完了. 感觉棒棒的. 哈, 你看出来了, 如果把这种方法用到强化学习, 岂不是 “牛逼lity”.

平行训练

alt text

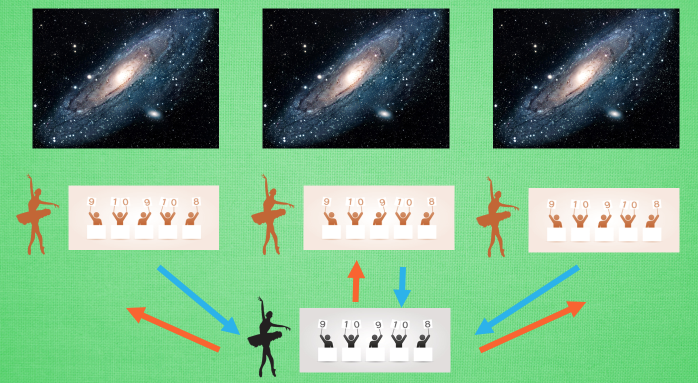
这就是传说中的 A3C. A3C 其实只是这种平行方式的一种而已, 它采用的是我们之前提到的 Actor-Critic 的形式. 为了训练一对 Actor 和 Critic, 我们将它复制多份红色的, 然后同时放在不同的平行宇宙当中, 让他们各自玩各的. 然后每个红色副本都悄悄告诉黑色的 Actor-Critic 自己在那边的世界玩得怎么样, 有哪些经验值得分享. 然后还能从黑色的 Actor-Critic 这边再次获取综合考量所有副本经验后的通关秘籍. 这样一来一回, 形成了一种有效率的强化学习方式.

多核训练

alt text

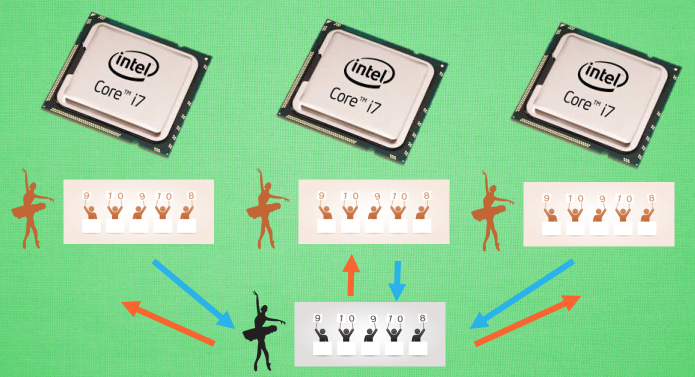
我们知道目前的计算机多半是有双核, 4核, 甚至 6核, 8核. 一般的学习方法, 我们只能让机器人在一个核上面玩耍. 但是如果使用 A3C 的方法, 我们可以给他们安排去不同的核, 并行运算. 实验结果就是, 这样的计算方式往往比传统的方式快上好多倍. 那我们也多用用这样的红利吧.

要点

一句话概括 A3C: Google DeepMind 提出的一种解决 Actor-Critic 不收敛问题的算法. 它会创建多个并行的环境, 让多个拥有副结构的 agent 同时在这些并行环境上更新主结构中的参数. 并行中的 agent 们互不干扰, 而主结构的参数更新受到副结构提交更新的不连续性干扰, 所以更新的相关性被降低, 收敛性提高.

因为这节内容是基于 Actor-Critic, 所以还不了解 Actor-Critic 的朋友们, 强烈推荐你在这个短视频 和这个 Python 教程中获得了解,

下面是这节内容的效果提前看:

算法

A3C 的算法实际上就是将 Actor-Critic 放在了多个线程中进行同步训练. 可以想象成几个人同时在玩一样的游戏, 而他们玩游戏的经验都会同步上传到一个中央大脑. 然后他们又从中央大脑中获取最新的玩游戏方法.

这样, 对于这几个人, 他们的好处是: 中央大脑汇集了所有人的经验, 是最会玩游戏的一个, 他们能时不时获取到中央大脑的必杀招, 用在自己的场景中.

对于中央大脑的好处是: 中央大脑最怕一个人的连续性更新, 不只基于一个人推送更新这种方式能打消这种连续性. 使中央大脑不必有用像 DQN, DDPG 那样的记忆库也能很好的更新.

为了达到这个目的, 我们要有两套体系, 可以看作中央大脑拥有 global net 和他的参数, 每位玩家有一个 global net 的副本 local net, 可以定时向 global net 推送更新, 然后定时从 global net 那获取综合版的更新.

如果在 tensorboard 中查看我们今天要建立的体系, 这就是你会看到的.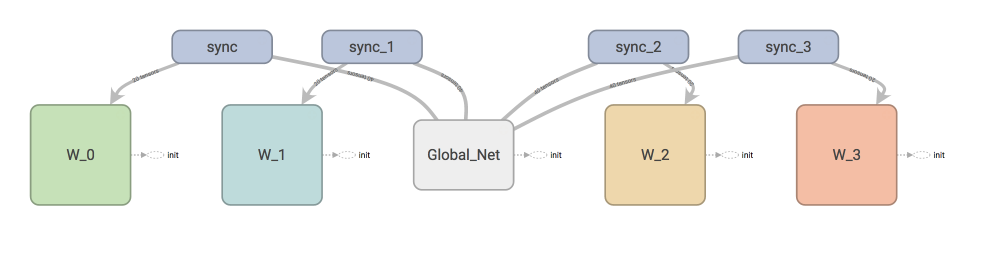

W_0 就是第0个 worker, 每个 worker 都可以分享 global_net.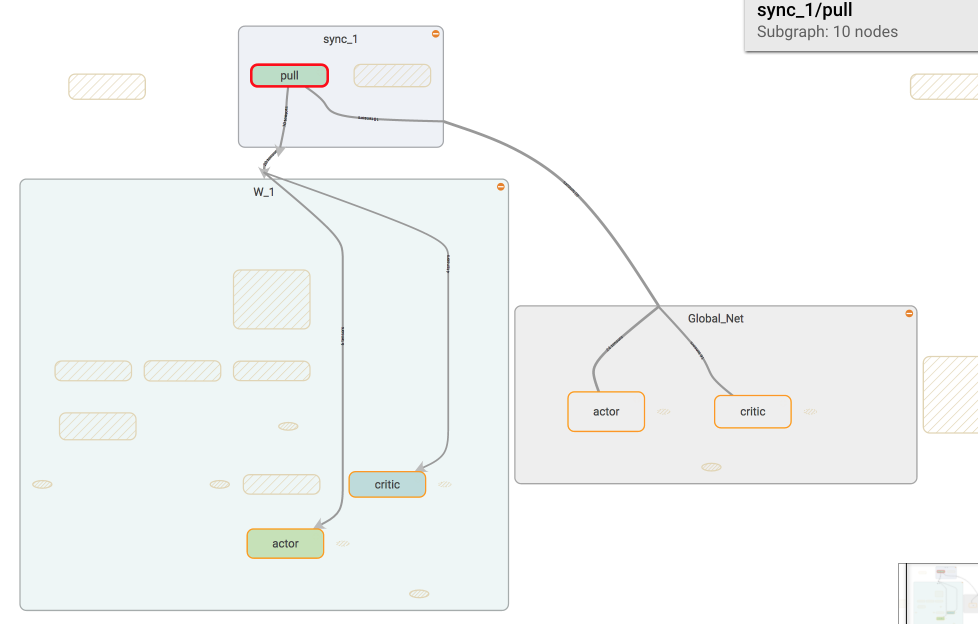

如果我们调用 sync 中的 pull, 这个 worker 就会从 global_net 中获取到最新的参数.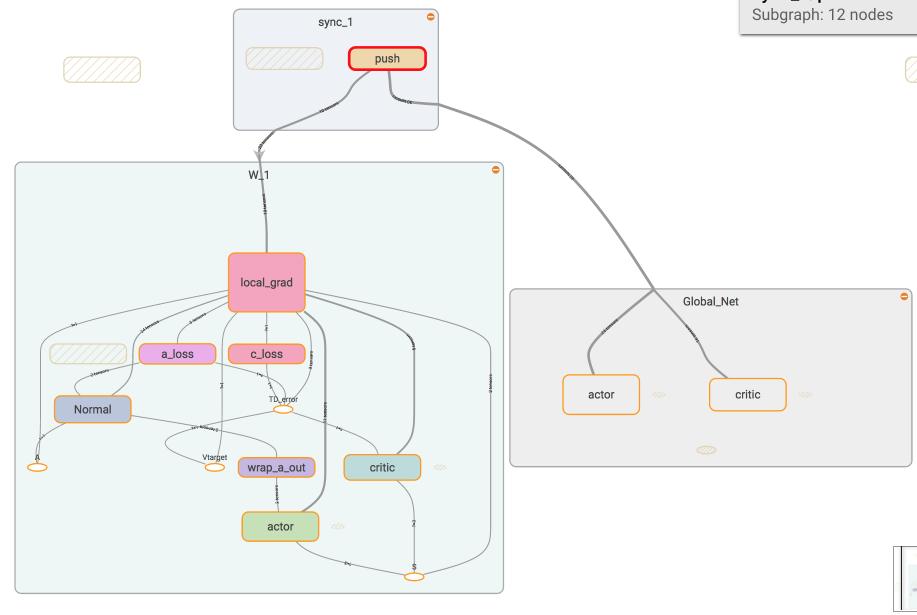

如果我们调用 sync 中的 push, 这个 worker 就会将自己的个人更新推送去 global_net.

这次我们使用一个连续动作的环境 Pendulum 举例. 如果直接看所有代码, 请看我的 Github, 如果你处理的是一个离散动作环境, 可以参考这个Github 中的这个文件.

接下来我们就开始定义连续动作的 A3C 啦.

主结构

我们用 Tensorflow 搭建神经网络, 对于我们的 Actor, tensorboard 中可以看清晰的看到我们是如果搭建的: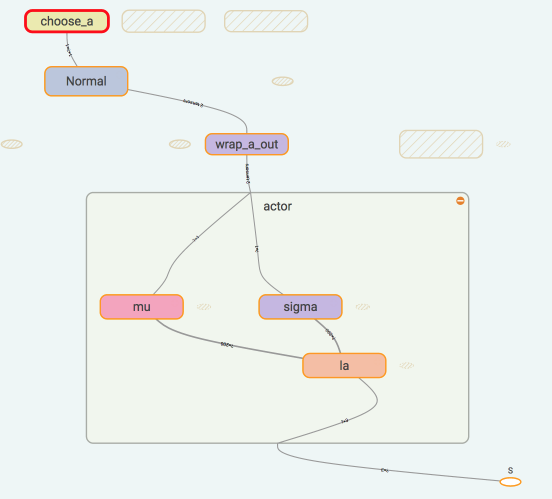

我们使用了 Normal distribution 来选择动作, 所以在搭建神经网络的时候, actor 这边要输出动作的均值和方差. 然后放入 Normal distribution 去选择动作. 计算 actor loss 的时候我们还需要使用到 critic 提供的 TD error 作为 gradient ascent 的导向.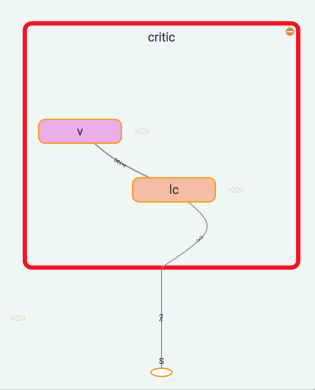

critic 很简单啦, 只需要得到他对于 state 的价值就好了. 用于计算 TD error.

Actor Critic 网络

我们将 Actor 和 Critic 合并成一整套系统, 这样方便运行.

# 这个 class 可以被调用生成一个 global net.
# 也能被调用生成一个 worker 的 net, 因为他们的结构是一样的,
# 所以这个 class 可以被重复利用.
class ACNet(object):
    def __init__(self, globalAC=None):
        # 当创建 worker 网络的时候, 我们传入之前创建的 globalAC 给这个 worker
        if 这是 global:   # 判断当下建立的网络是 local 还是 global
            with tf.variable_scope('Global_Net'):
                self._build_net()
        else:
            with tf.variable_scope('worker'):
                self._build_net()

            # 接着计算 critic loss 和 actor loss
            # 用这两个 loss 计算要推送的 gradients

            with tf.name_scope('sync'):  # 同步
                with tf.name_scope('pull'):
                    # 更新去 global
                with tf.name_scope('push'):
                    # 获取 global 参数

    def _build_net(self):
        # 在这里搭建 Actor 和 Critic 的网络
        return 均值, 方差, state_value

    def update_global(self, feed_dict):
        # 进行 push 操作

    def pull_global(self):
        # 进行 pull 操作

    def choose_action(self, s):
        # 根据 s 选动作

这些只是在创建网络而已, worker 还有属于自己的 class, 用来执行在每个线程里的工作.

Worker

每个 worker 有自己的 class, class 里面有他的工作内容 work, 看全部请来我的 Github.

alt text

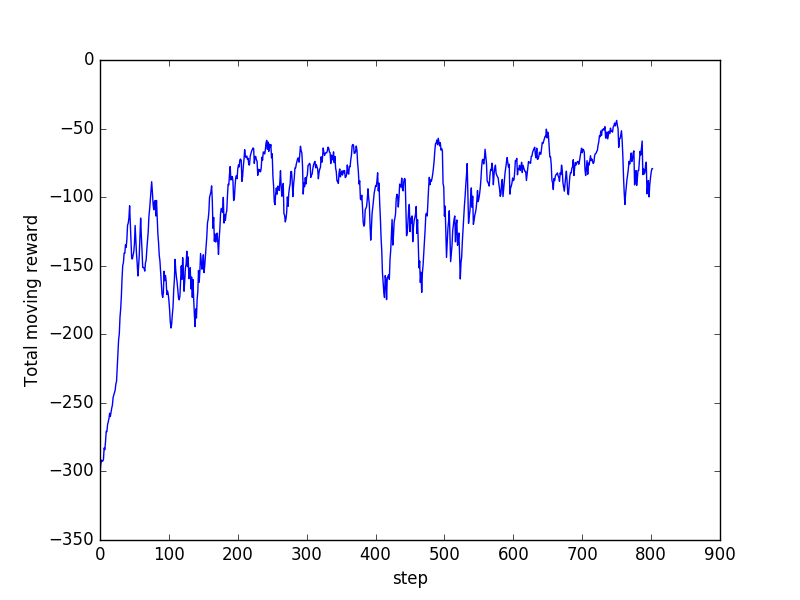
上面讲到的是一个 continuous action 的例子, 全部代码在这里清晰可见. 还有一个是 discrete action 的例子. 使用的是 Cartpole 的实验, 代码在这. 同时, 我还做了一个 A3C 加上 RNN 的例子, 同样是用 Pendulum 的例子, 代码在这.

multiprocessing + A3C

除此之外, 我心里一直有一个疙瘩, 因为这个 A3C 中, 我用的是 python 的 threading, 懂 python 的朋友知道, threading 有 GIL, 运算速度是问题, 我的 CPU 都不是满格的. 我一直想把这个 A3C 代码移植去 multiprocessing, 提高效率. 但是 Tensorflow 的 session 就是和 multiprocessing 不兼容, Global Net 做不好. 怎么办?

Distributed Tensorflow 是一个备选方案. 但是这个要求你是在计算机集群上做, 不然速度上还不如这个 threading 的 A3C. 这时, 我不爽了, 到在知乎上抱怨了一番. 和知友们聊了会, 然后我想出了下面这个方案.

和 Tensorflow 一样, 我做过一些 Pytorch 的教程, pytorch 也是做神经网络的. 但是它是支持 multiprocessing 的. 我专门开了一个 repo, 把 Pytorch + multiprocessing 的代码分享了出来. 这会儿, CPU 满格, 心情舒畅多了~