手写机器学习正向传播和反向传播
https://www.cnblogs.com/charlotte77/p/5629865.html
我保存到了 pdf 中《一文弄懂神经网络中的反向传播法——BackPropagation.pdf》
参考链接
1 | #coding:utf-8 |
机器学习分类
根据训练数据是否有标签,可以分为:
监督学习:所有训练数据均具有标签(典型的问题有回归:模型输出的是一个具体数值;分类:模型的输出是某一类别) 在监督学习中,常用的模型种类可以分为:线性模型 和 非线性模型。其中,非线性模型应用更加广泛,表达能力也更强,包括深度学习,支持向量机(SVM),决策树,K-NN算法等。
半监督学习:训练数据中,部分具有标签,另一部分没有标签(但是没有标签的数据,对于模型的学习也是有用处的)。 迁移学习:使用与当前任务无关的数据(可能有标签,可能没有标签)来促进当前模型的学习。 无监督学习:训练数据都没有标签。 无监督学习存在的原因是,现实世界中,为训练数据进行标注成本较高,当训练数据都没有标签时,如果我们想要为数据进行分类,只能根据数据的特征进行划分,比如聚类算法。
强化学习:训练数据没有标签,智能体从环境交互中进行学习,来更新自身的策略,根据最终环境的反馈(获得的奖励)来调整自身行为。
回归问题
机器学习笔记的第二篇博客,来介绍机器学习中最基础的回归任务,上一篇博客中有提到回归任务和分类任务的差别在于,回归任务中模型的输出是一个具体的数值, 而分类任务中模型的输出是某一类别。其实,许多问题我们都可以视为回归问题:例如:根据股票市场的历史数据预测明天的股票走势;自动驾驶中根据传感器获取的信息输出方向盘的转动角度;推荐系统中,输入用户和商品的特征,模型输出一个[0,1]之间的数值,表示购买的可能性。
回归模型的建立
机器学习模型建立的三个步骤:
- 我们准备许多备选的函数 f ,构成一个集合,也就是机器学习中的模型(Model)。
- 使用训练数据来衡量这些备选函数的好坏程度。
- 根据训练数据选出拟合最好的函数,作为最终的拟合函数。
第一步:确定用于回归任务的模型
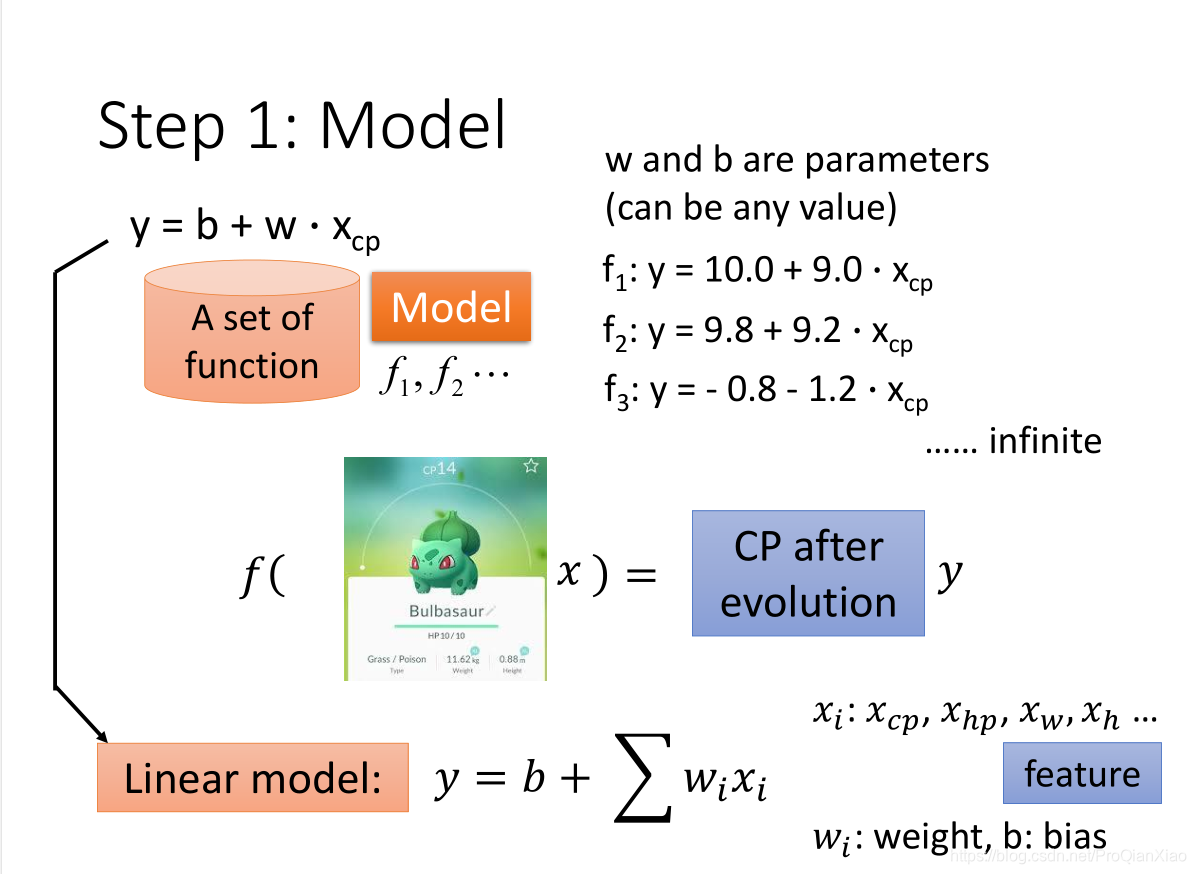
这里选择一元线性函数 y = wx + b即线性模型,一元表示我们使用的特征是一个(宝可梦的原CP值);这样我们就构造了一个函数集合,由于参数w和b的取值是无穷的,所以函数集合中函数的个数是无穷个,接下来在函数集合中选择最好的函数的过程实际上就是为函数确定参数值的过程。
第二步:使用训练数据来衡量这些备选函数的好坏程度(确定参数)

接下来我们需要根据训练数据来从备选函数中选择一个效果最好的函数(即确定函数参数部分),这里需要使用损失函数,损失函数的输入是 “用来进行回归任务的函数” 和 “真实标签” ,输出是 进行回归任务的函数的好坏程度(Loss的值越小,认为该函数的效果越好)。如上图所示,我们使用 平方差之和 作为损失函数。
第三步:根据训练数据选出拟合最好的函数,作为最终的拟合函数
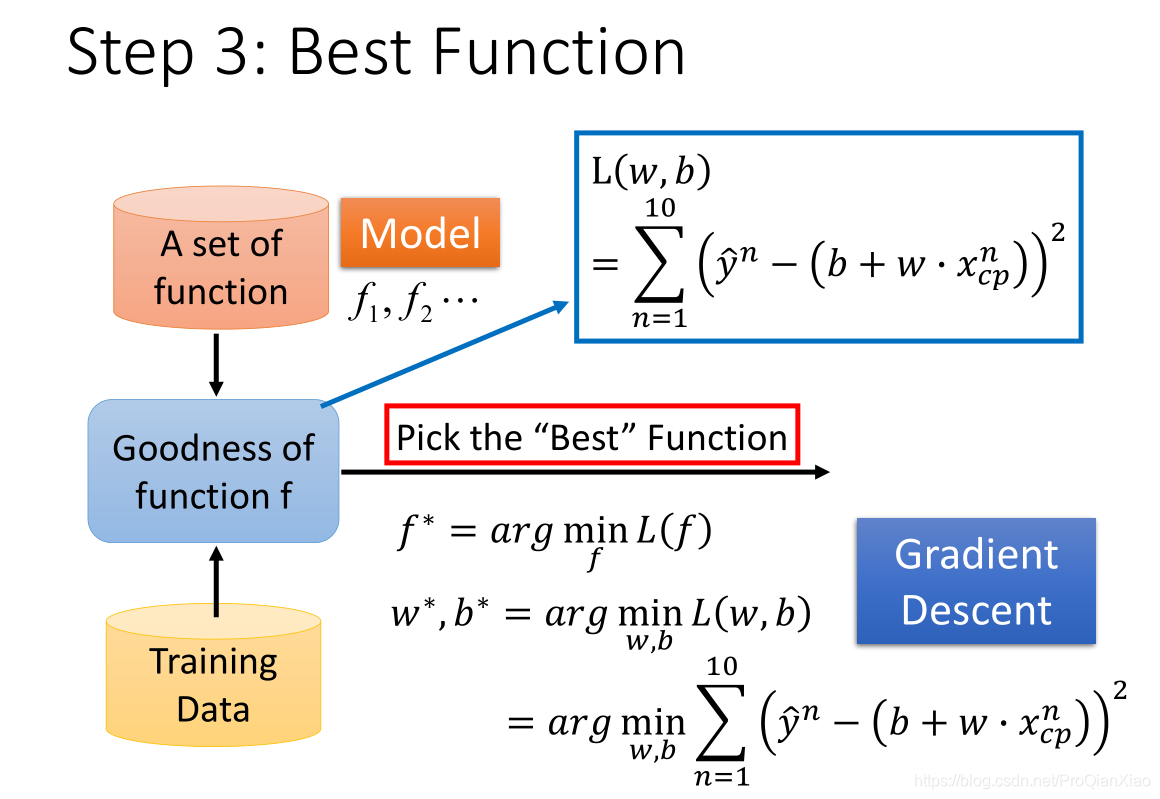
第三步,我们在训练数据上根据损失函数来评估拟合函数的好坏,找到使得损失函数最小的一组参数,作为我们最终的拟合函数。其中,寻找参数时,使用的方法为 梯度下降法 。
梯度下降
梯度下降算法是机器学习领域最广为人知、用途最广的优化算法,用来确定模型的参数(包括随机梯度下降SGD,Momentum,Adam等)。梯度下降算法的一个简单介绍如下:
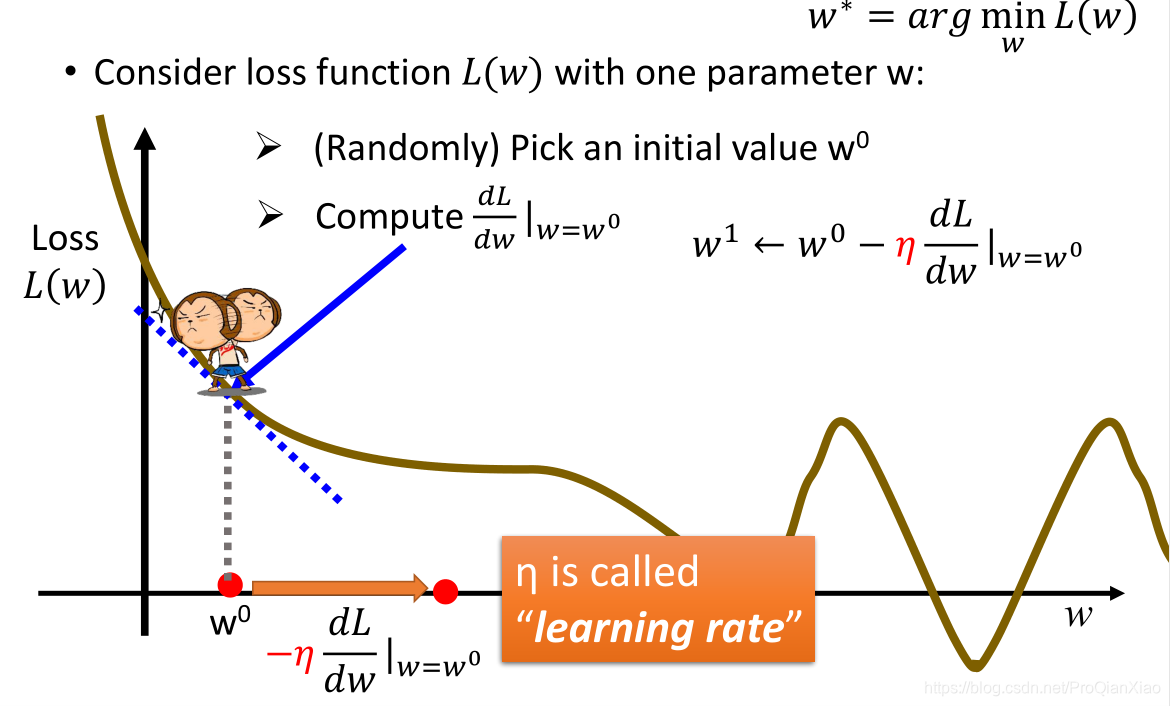

1、在机器学习中,只要损失函数是可微分(可求导)的,就可以使用梯度下降算法进行参数的求解,那么怎么判断损失函数是否可微?(后面解释)
上面图片展示的是,模型当中只有一个参数(所以直接对该参数求导就可以),如果模型中存在两个及以上的参数,那么就需要分别对每个参数计算偏导数,然后根据参数更新公式进行每个参数的更新,如下图所示:

梯度下降算法的原理已经清楚,其实就是沿着损失函数降低的方向更新模型的参数,但是如果损失函数很复杂,比如下面图片所示,
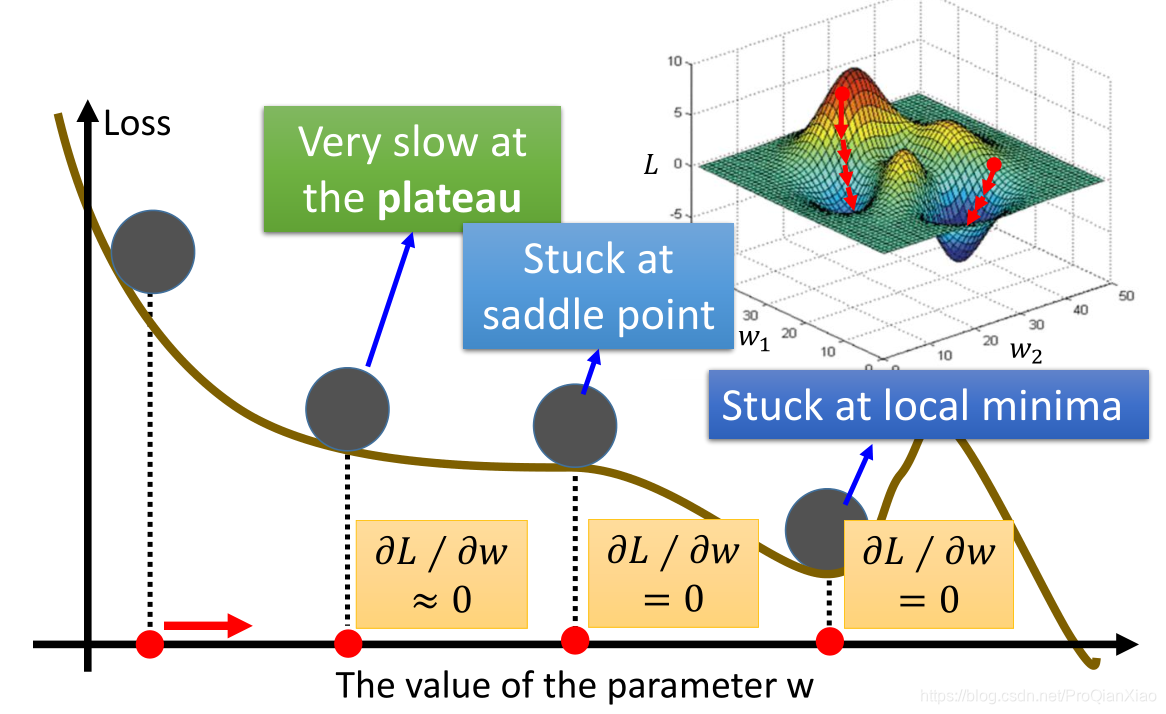
我们很可能在更新参数的过程中,走到导数为0的点(第四个红点位置),这时因为不知道更新的方向,就陷入了局部最优点(其实真正的全局最优点还在右边)。
2、不过对于上面回归问题中,损失函数为平方差之和,该损失函数为凸函数,没有局部最优点,只有全局最优点。那么如何判断一个函数是否为凸函数?(后面解释)
预测结果分析
我们上面的线性模型,经过梯度下降算法,寻得一组最优参数,其结果表现如下:
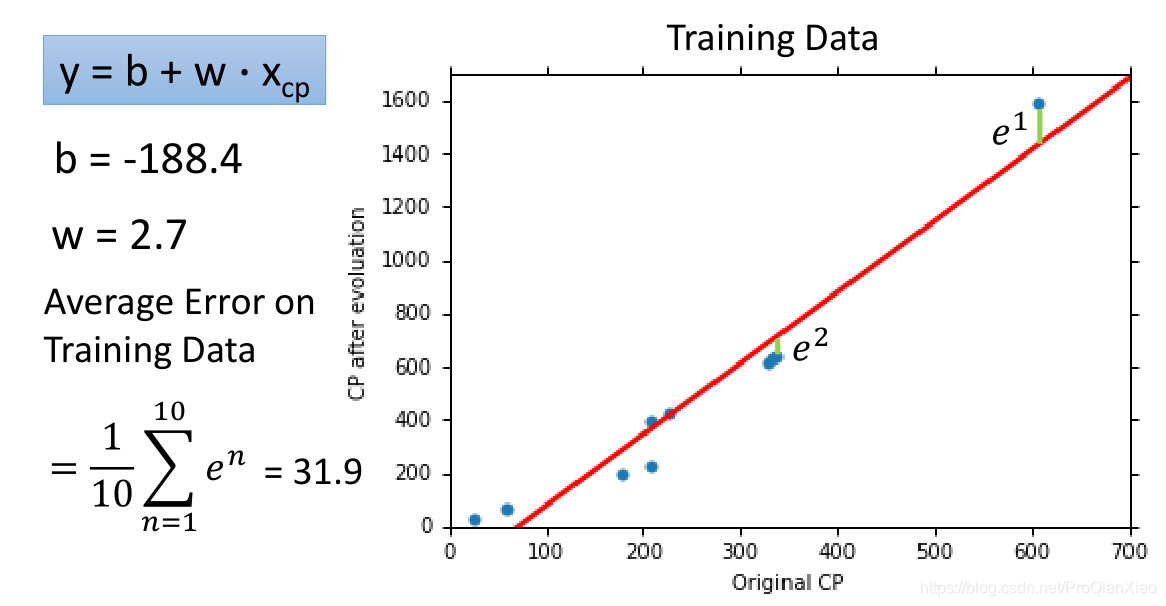
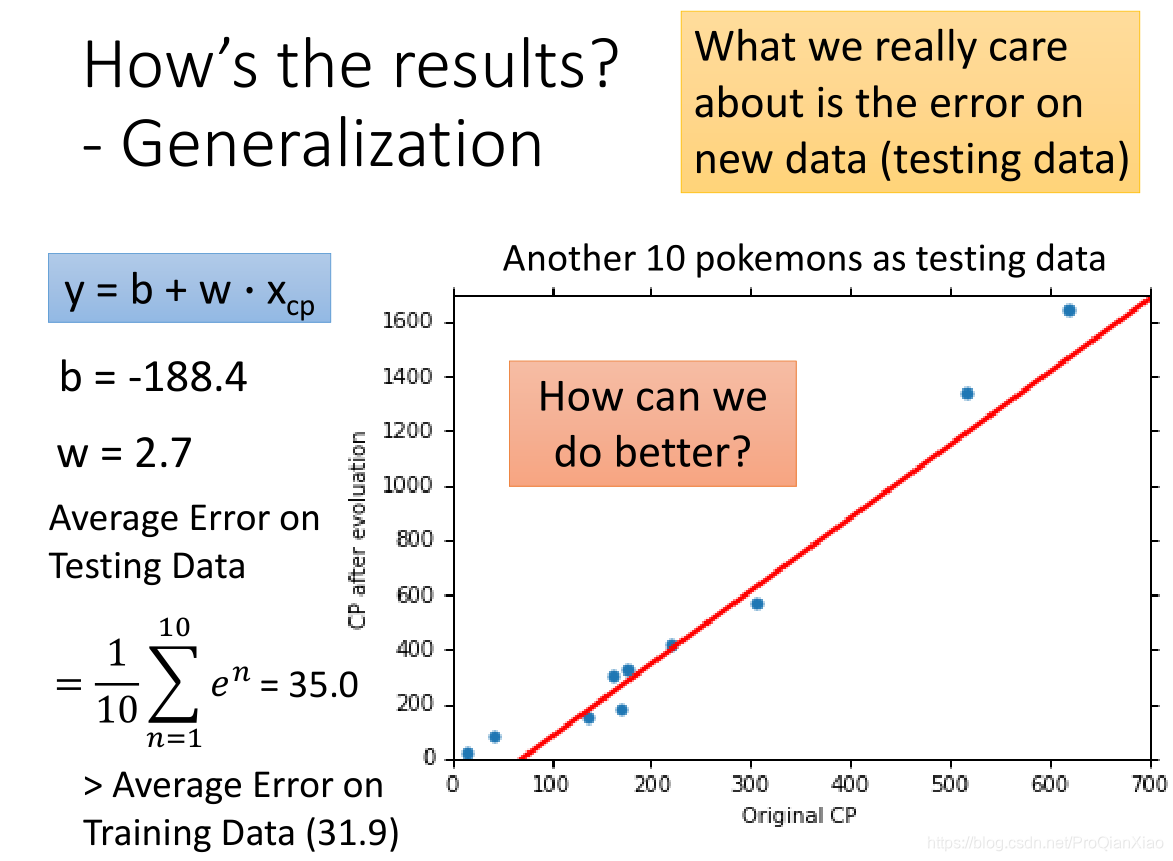
训练数据上面的损失函数值为31.9,测试数据上面损失函数值为35。在实际问题中,我们更加关注的是模型在测试集上面的性能表现,也就是模型的
泛化能力
,线性模型在测试集上面的误差较大,所以如果我们重新设计预测模型,使用更加复杂的模型,会不会得到更好的效果?
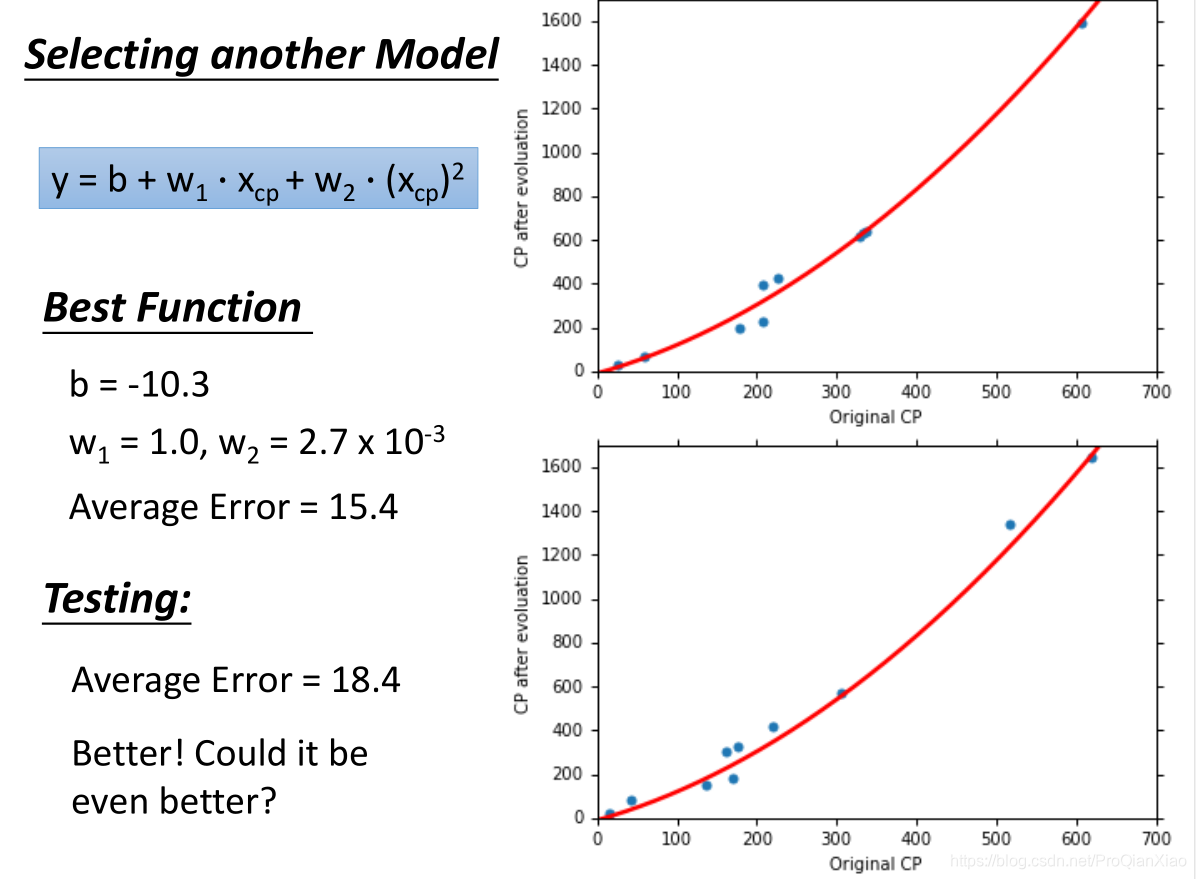
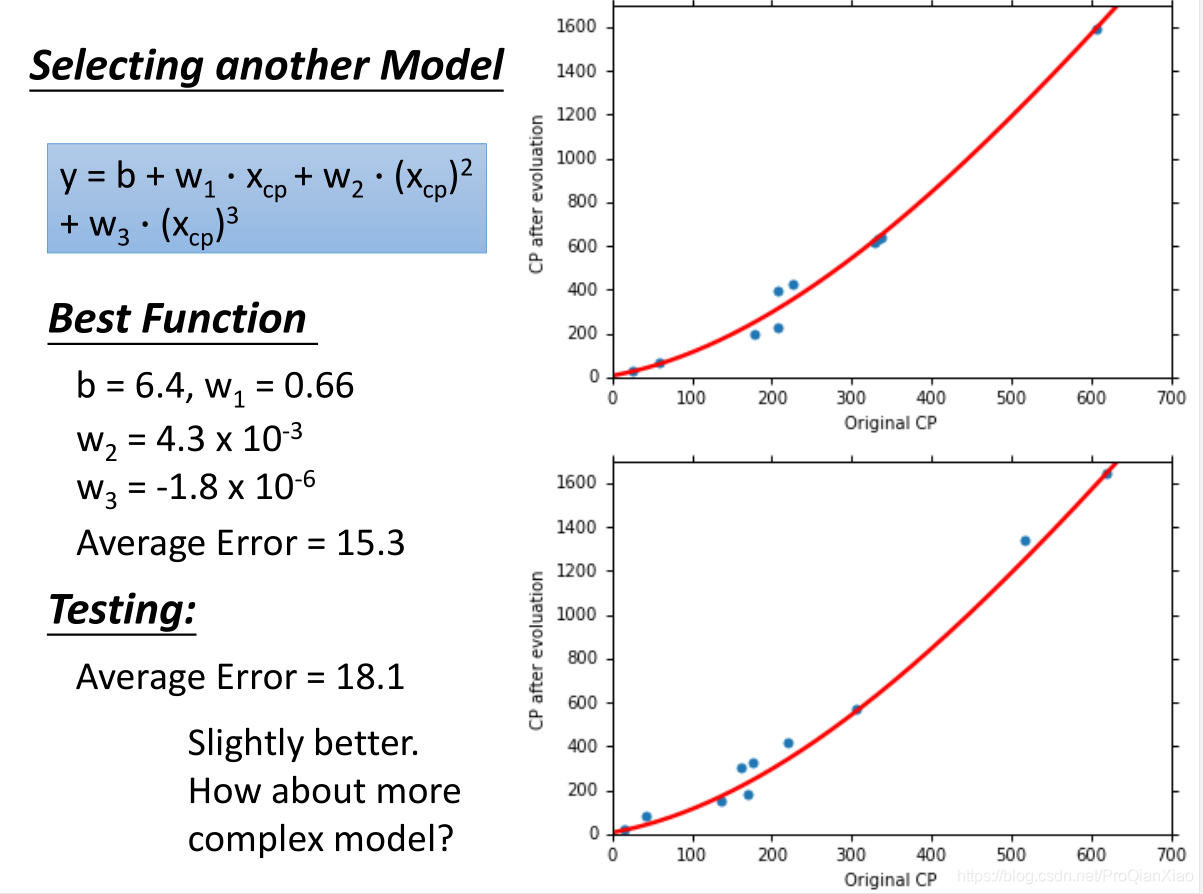
随着使用更加复杂的二次模型,三次模型,无论是在训练集还是测试集上面,效果都有提升。可是当继续增加模型的复杂度,使用四次模型的时候,虽然在训练集上面的loss更小,但是测试集上面的效果却变糟了。使用五次模型的时候,这一趋势更加明显:
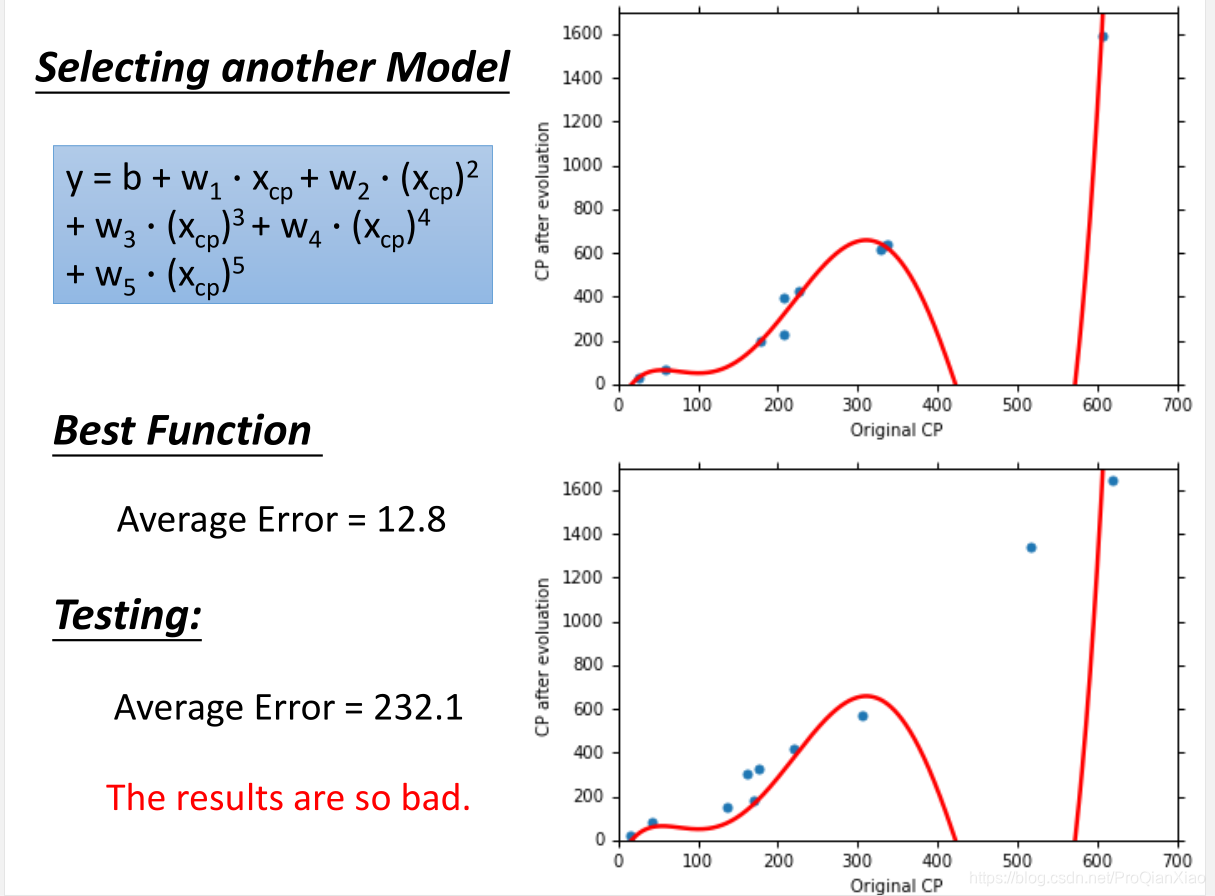 虽然复杂的模型对于训练数据的拟合程度会更好,但是很容易出现过拟合的现象(过于严格的去拟合训练数据,当面对新数据的时候没有办法做出准确的预测,即无法泛化到其他数据)。
虽然复杂的模型对于训练数据的拟合程度会更好,但是很容易出现过拟合的现象(过于严格的去拟合训练数据,当面对新数据的时候没有办法做出准确的预测,即无法泛化到其他数据)。
 在机器学习模型训练过程中,我们要尽量避免过拟合的现象,一方面要选择合适的模型,模型不是越复杂越好,可以通过交叉验证来选择合适的模型;另一方面,可以通过一些技术手段来帮助我们避免过拟合,比如正则化,early
stopping等等。
在机器学习模型训练过程中,我们要尽量避免过拟合的现象,一方面要选择合适的模型,模型不是越复杂越好,可以通过交叉验证来选择合适的模型;另一方面,可以通过一些技术手段来帮助我们避免过拟合,比如正则化,early
stopping等等。 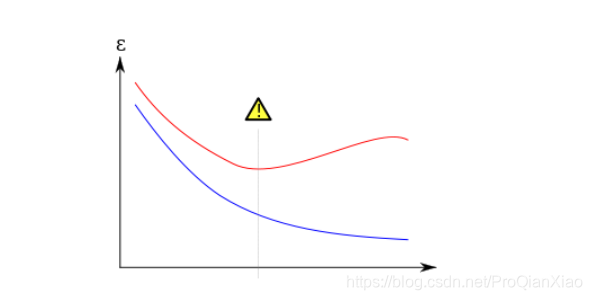 如上图所示,蓝色线代表训练集上的损失函数,红色线代表验证集的损失函数,当训练进行到中间垂直的线段时,模型应该是最优的;如果继续训练,就会造成过拟合现象。
如上图所示,蓝色线代表训练集上的损失函数,红色线代表验证集的损失函数,当训练进行到中间垂直的线段时,模型应该是最优的;如果继续训练,就会造成过拟合现象。
正则化

简单来说,正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。我们在构造机器学习模型时,最终目的是让模型在面对新数据的时候,可以有很好的表现。当使用比较复杂的模型比如神经网络,去拟合数据时,很容易出现过拟合现象(训练集表现很好,测试集表现较差),这会导致模型的泛化能力下降,这时候,就需要使用正则化,降低模型的复杂度。
具体而言,正则化就是在损失函数后面增加一项惩罚项(对某些参数进行限制),使得我们的模型更加平滑。以上图为例,我们在损失函数后面增加一项关于参数w的正则项,限制参数w不要过大,这样模型会有更好的泛化能力。因为,这样对于测试数据中存在的噪声,会不那么敏感,即噪声对于预测的结果影响会降低。

加入正则化技术之后,训练集和测试集上面的误差如下: 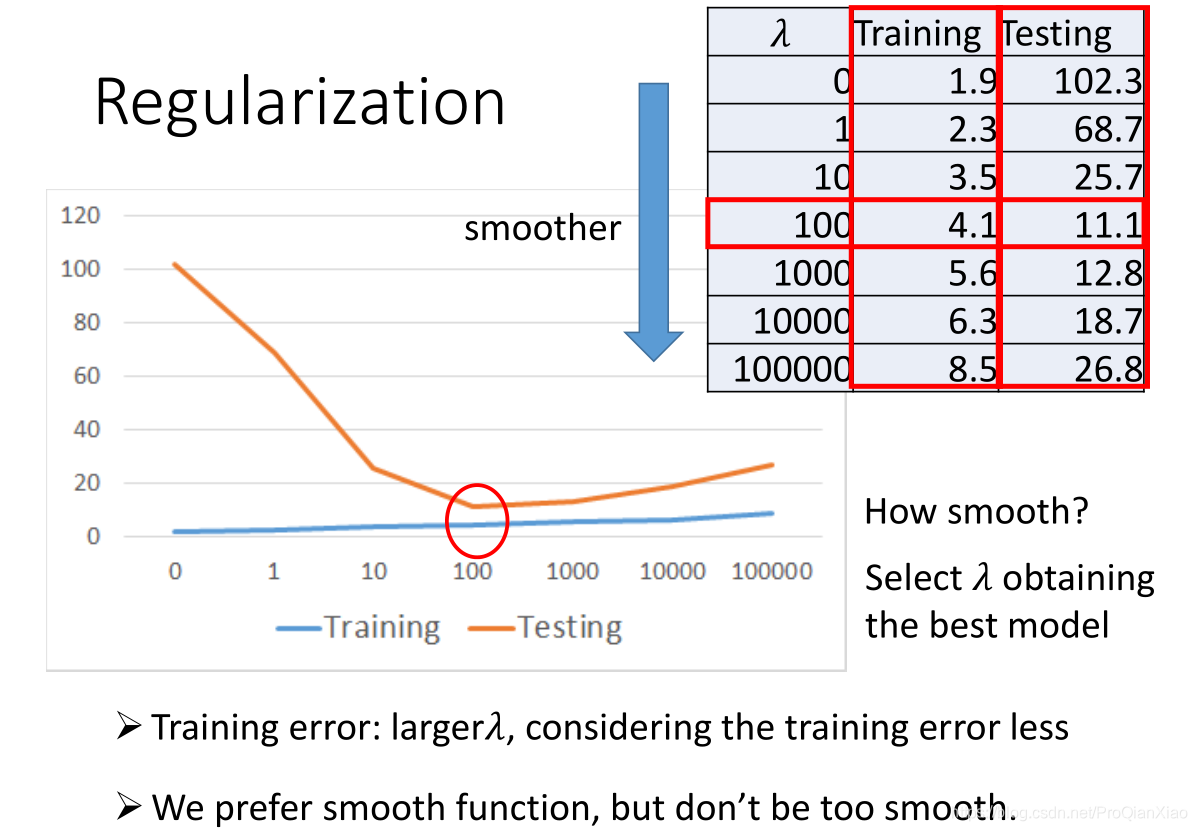
和我们的预期分析是一致的,加入正则化之后,参数
越大,表示我们越关注模型的平滑程度(也就是模型的泛化能力),相对于训练误差考虑较少,所以训练集上面的loss增大,测试集上面的loss降低。但是,参数
不是越大越好,我们希望得到一个比较平滑的函数,但是不能过于平滑(会丧失其预测能力)。
机器学习中的正则化概念
在机器学习中,正则化(Regularization)是一种用于防止过拟合(Overfitting)的技术。
过拟合是指模型在训练数据上表现得非常好,但在新的、未见过的数据上表现不佳。这通常是因为模型过于复杂,学习到了训练数据中的噪声和特定的细节,而不是一般性的模式。
正则化通过在损失函数中添加一个惩罚项来限制模型的复杂度。常见的正则化方法有 L1 正则化和 L2 正则化。
L1 正则化:也称为 Lasso 正则化,它在损失函数中添加的惩罚项是模型参数的绝对值之和。L1 正则化具有特征选择的效果,因为它可能会将一些不重要的特征对应的参数压缩至零。
例如,在线性回归中,假设模型的预测函数为
y = w1 * x1 + w2 * x2 +... + wn * xn + b ,L1 正则化项就是
λ * |w1| + λ * |w2| +... + λ * |wn| ,其中 λ
是正则化参数,控制正则化的强度。
L2 正则化:也称为 Ridge 正则化,它在损失函数中添加的惩罚项是模型参数的平方和。L2 正则化会使模型的参数值趋向于较小的值,但不太会将参数压缩至零。
同样在线性回归中,L2 正则化项就是
λ * (w1^2 + w2^2 +... + wn^2) 。
正则化的作用:
- 控制模型复杂度:通过限制模型的参数大小,防止模型过于复杂。
- 提高模型泛化能力:使模型能够更好地应对新的数据,减少过拟合的风险。
举例说明: 假设我们正在训练一个神经网络来识别图像中的猫和狗。如果没有正则化,模型可能会过度学习训练数据中的细微特征,比如图片中的背景颜色或微小的噪声,导致在新的图像上识别准确率下降。
当我们应用 L2 正则化时,模型的参数会受到一定的约束,不会变得过大。这可能会导致模型在训练数据上的准确率稍微降低,但在测试数据上的表现会更好,因为它学习到了更通用的特征,而不是过度依赖于特定的训练样本。
总之,正则化是机器学习中非常重要的技术,有助于提高模型的性能和稳定性。
遗留问题
1、在机器学习中,只要损失函数是可微的,就可以使用梯度下降算法进行参数的求解,那么怎么判断损失函数是否可微?(后面解释)
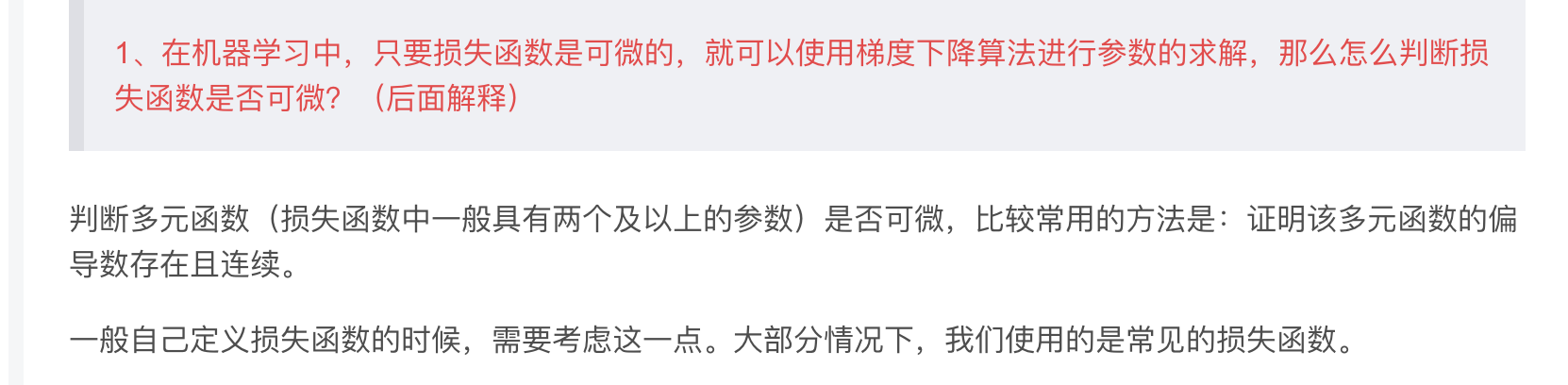
2、不过对于上面回归问题中,损失函数为平方差之和,该损失函数为凸函数,没有局部最优点,只有全局最优点。那么如何判断一个函数是否为凸函数?(后面解释)


判断一个矩阵是不是半正定矩阵,方法之一是判断该矩阵的所有主子式是不是非负;对于上面的海森矩阵,其所有主子式为:
半正定矩阵
半正定矩阵是矩阵理论中的一个重要概念。
一个实对称矩阵 A
被称为半正定矩阵,如果对于任意的非零实向量 x ,都有
x^T Ax ≥ 0 。
性质 :
- 半正定矩阵的所有特征值都是非负的。
- 半正定矩阵的主子式都非负。
- 半正定矩阵与另一个半正定矩阵的和仍是半正定矩阵。
在实际的机器学习和优化问题中,Hessian 矩阵具有重要的地位。
计算方面: 计算 Hessian 矩阵可能是计算密集型的,特别是对于具有大量参数的模型。在深度学习中,直接计算完整的 Hessian 矩阵通常是不现实的。然而,可以使用近似方法或针对特定结构的模型进行简化计算。例如,对于一些具有简单结构的神经网络,可能通过一些技巧来估计 Hessian 矩阵的部分元素。
应用方面:
- 优化算法:如牛顿法及其变体,利用 Hessian
矩阵来确定搜索方向和步长。相比于梯度下降法只依赖一阶导数(梯度),牛顿法考虑了二阶导数信息,能够在一些情况下更快地收敛到最优解。
- 举例来说,在求解一个二次函数的最小值时,牛顿法通过一次迭代就可以直接到达最小值点,因为它准确地利用了 Hessian 矩阵的信息。
- 模型分析:帮助理解模型的性质和行为。通过分析 Hessian
矩阵的特征值和特征向量,可以了解模型在不同方向上的敏感度和曲率,从而洞察模型的稳定性和鲁棒性。
- 例如,在图像分类任务中,如果 Hessian 矩阵的某些特征值很大,说明模型在对应的特征方向上变化剧烈,可能对输入的微小变化非常敏感。
- 正则化:可以用于设计一些基于二阶信息的正则化方法,以防止过拟合。
- 比如,通过对 Hessian 矩阵进行某种变换或约束,使得模型的复杂度得到控制。
总之,尽管在实际中直接处理 Hessian 矩阵存在困难,但通过巧妙的近似和应用,它仍然为解决机器学习和优化问题提供了有价值的见解和工具。
梯度下降算法
梯度下降算法是机器学习领域最广为人知、用途最广的优化算法,用来确定模型的参数(包括随机梯度下降SGD,Momentum,Adam等)。首先回顾一下梯度下降的计算过程:
梯度下降中常用技巧(Tips)
一、调整学习率
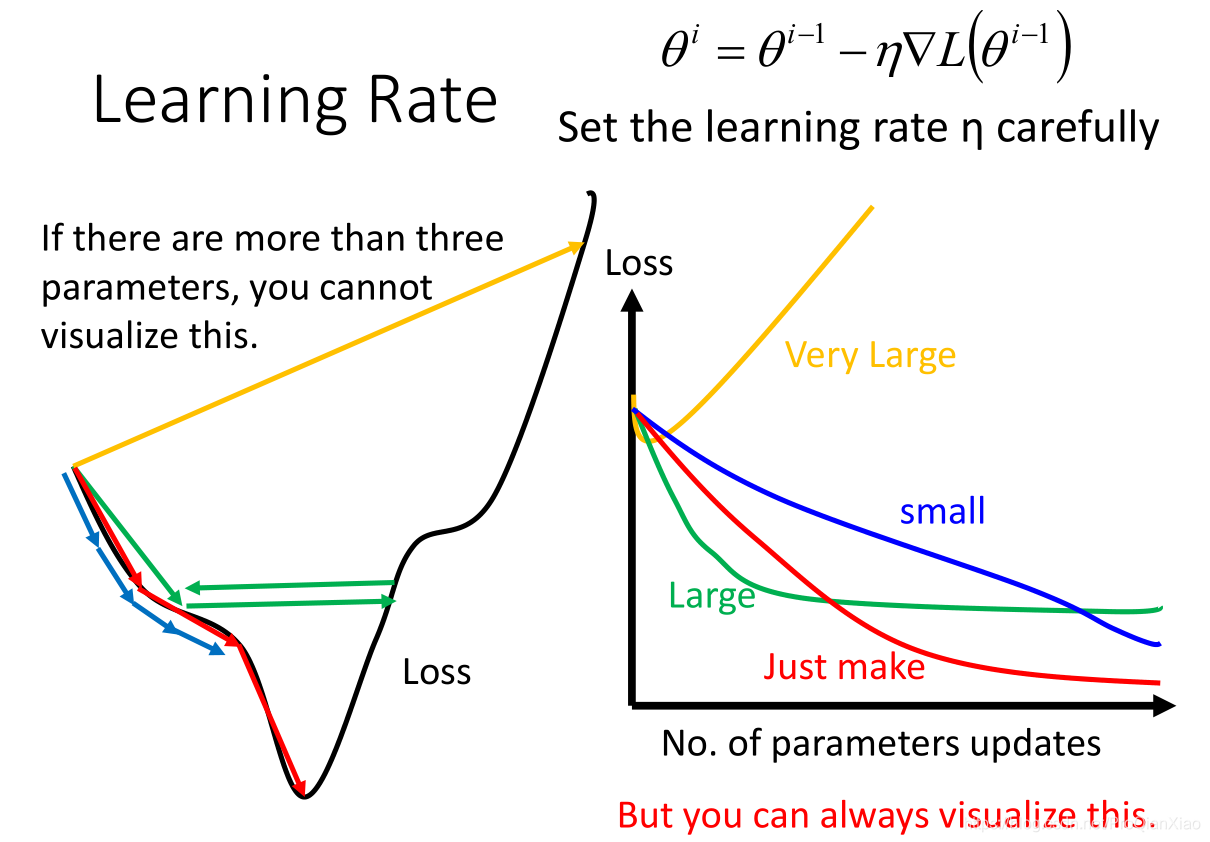

所以,我们可以根据Loss曲线的变化情况,对我们的学习率进行一个合理的调整。可以绘制上图右边部分所示的曲线图,横轴代表参数更新次数,纵轴代表Loss值,学习率的大小分为四种情况:

在学习率的设置过程中,常见的做法是,进行 学习率的衰减 。

在模型训练初期,距离全局最优点较远,可以设置一个相对大一些的学习率,随着训练的进行,距离全局最优点的距离越来越小,此时应该减小学习率;所以让学习率随着时间或者更新的次数进行衰减。
除了学习率的衰减之外,另外一个做法是:为不同的参数设置不同的学习率。也就是接下来要介绍的一种优化算法AdaGrad。
AdaGrad优化器
AdaGrad(Adaptive Gradient Algorithm)是一种自适应学习率的方法,用于优化机器学习模型,特别是在处理稀疏数据和高维数据时表现出色。AdaGrad的主要特点是它为每个参数维护一个单独的学习率,并根据之前的梯度信息调整这些学习率。
AdaGrad根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,从而避免统一的学习率难以适应所有维度的问题,即为每个参数设置不同的学习率。具体来说,对于每个参数 θi,AdaGrad计算其所有历史梯度的平方和,并用这个和来缩放当前的梯度,从而得到更新步长。


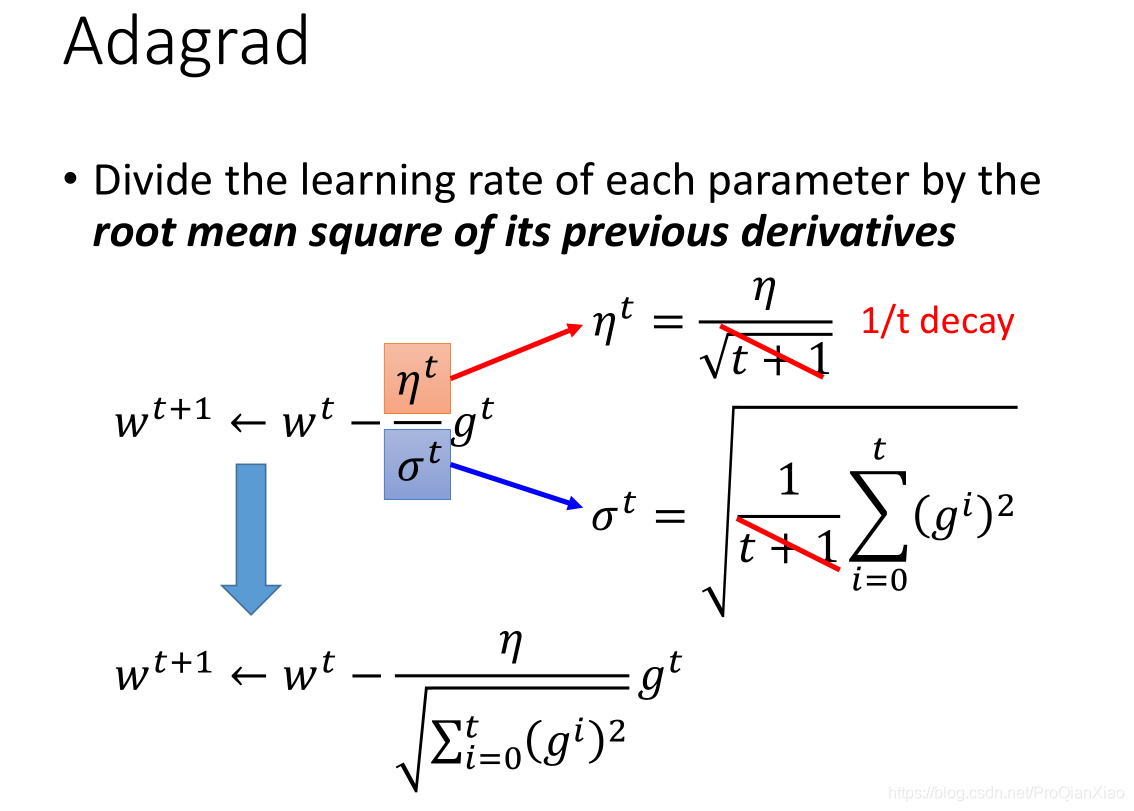
这里需要注意的一点为: 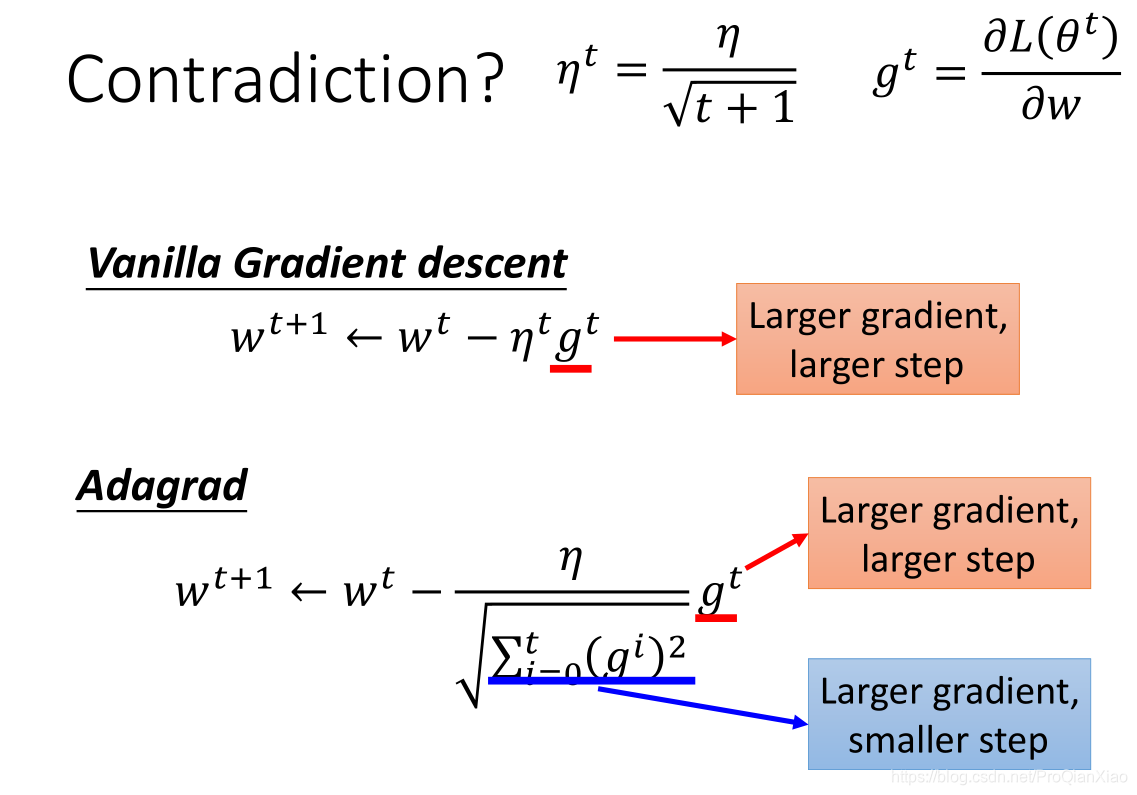

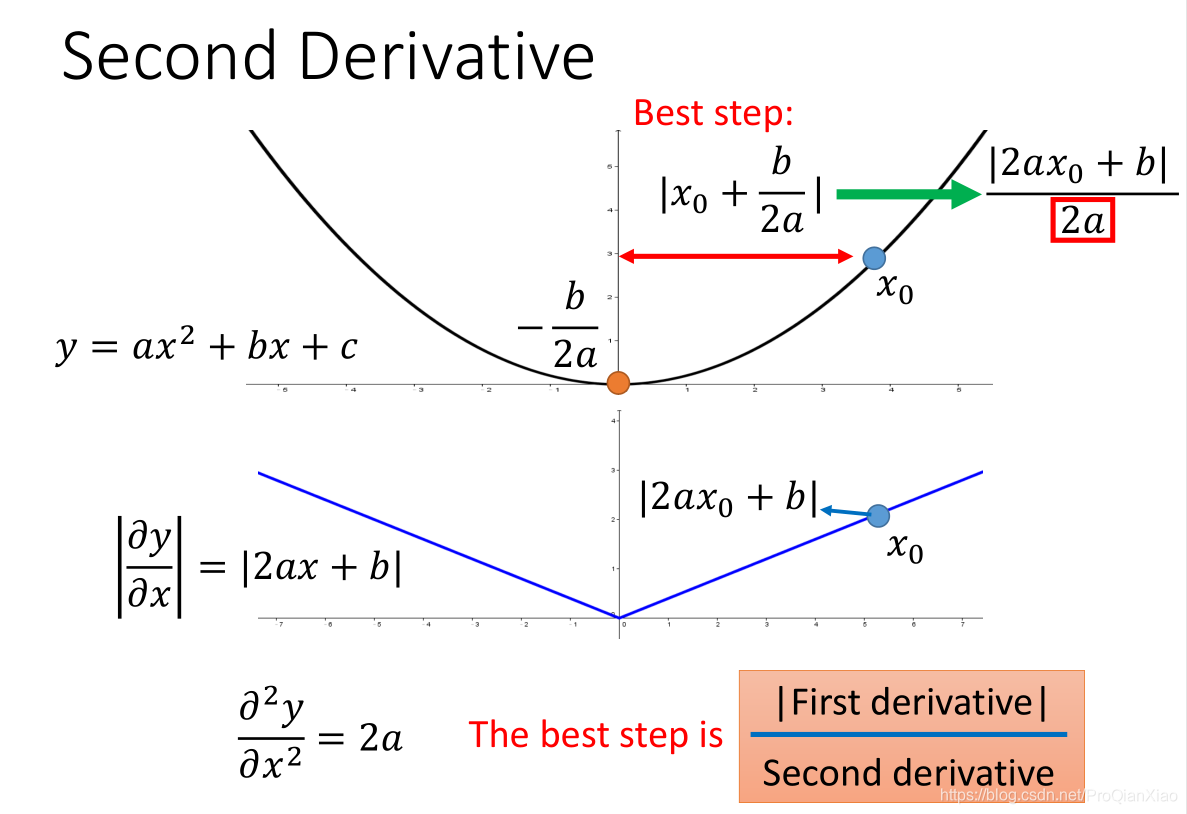
 而在AdaGrad中,正是这一思想的体现,不过为了减少计算量,增加运算速度,AdaGrad中使用过去一阶偏导数的均方根作为分母项(二阶偏导数)的近似。
而在AdaGrad中,正是这一思想的体现,不过为了减少计算量,增加运算速度,AdaGrad中使用过去一阶偏导数的均方根作为分母项(二阶偏导数)的近似。
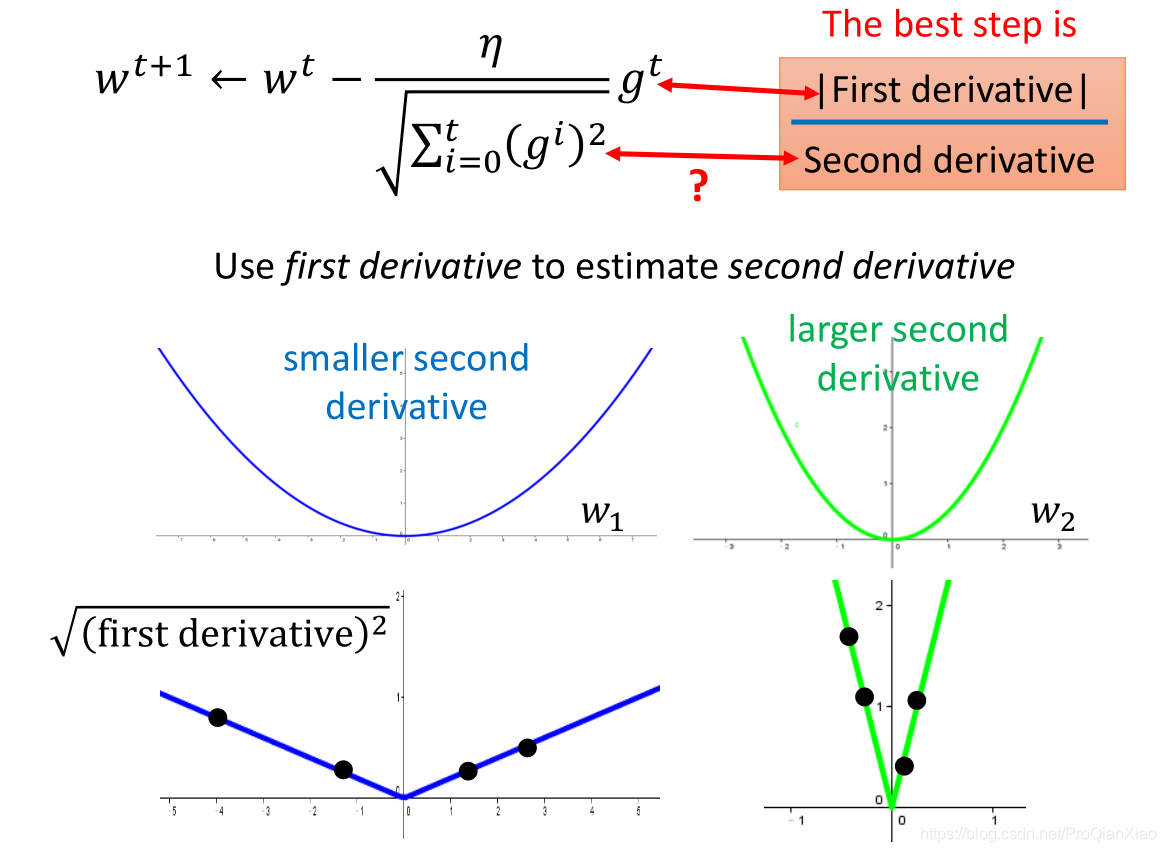 过去一阶偏导数的均方根可以在一定程度上反应二阶偏导的大小情况。如上图所示,二阶偏导小的函数,其采样的一阶偏导的值也相对较小。
过去一阶偏导数的均方根可以在一定程度上反应二阶偏导的大小情况。如上图所示,二阶偏导小的函数,其采样的一阶偏导的值也相对较小。
优势
- 自适应学习率 :不同参数有不同的学习率,能够更好地处理稀疏数据,使得更新幅度较大的参数的学习率更小,而更新幅度较小的参数的学习率更大。
- 简化调参 :由于学习率是自适应的,通常不需要频繁调整学习率超参数。
局限性
- 学习率过小 :随着时间的推移,累积梯度平方和不断增大,导致学习率逐渐缩小,可能会导致算法在后期学习变得非常缓慢。
- 不适用于所有问题 :虽然AdaGrad在处理稀疏数据上有优势,但对于某些问题,其性能可能不如其他优化算法,如RMSprop或Adam。
典型应用
AdaGrad常用于处理自然语言处理中的词嵌入、推荐系统中的用户行为数据等高维、稀疏数据场景。
总结来说,AdaGrad通过自适应地调整每个参数的学习率,在处理稀疏数据和高维数据时提供了显著的优势,但其逐渐减小的学习率可能在某些情况下限制其性能。
二、随机梯度下降(SGD)
随机梯度下降(SGD, Stochastic Gradient Descent)是一种用于优化机器学习模型参数的算法,特别适用于大规模数据集的训练。SGD与传统的批量梯度下降(Batch Gradient Descent)不同,它在每次迭代中仅使用一个样本或一个小批量的样本(mini-batch)来计算梯度和更新参数。这种方法具有较快的更新速度和更好的内存效率,特别是在处理大数据集时。


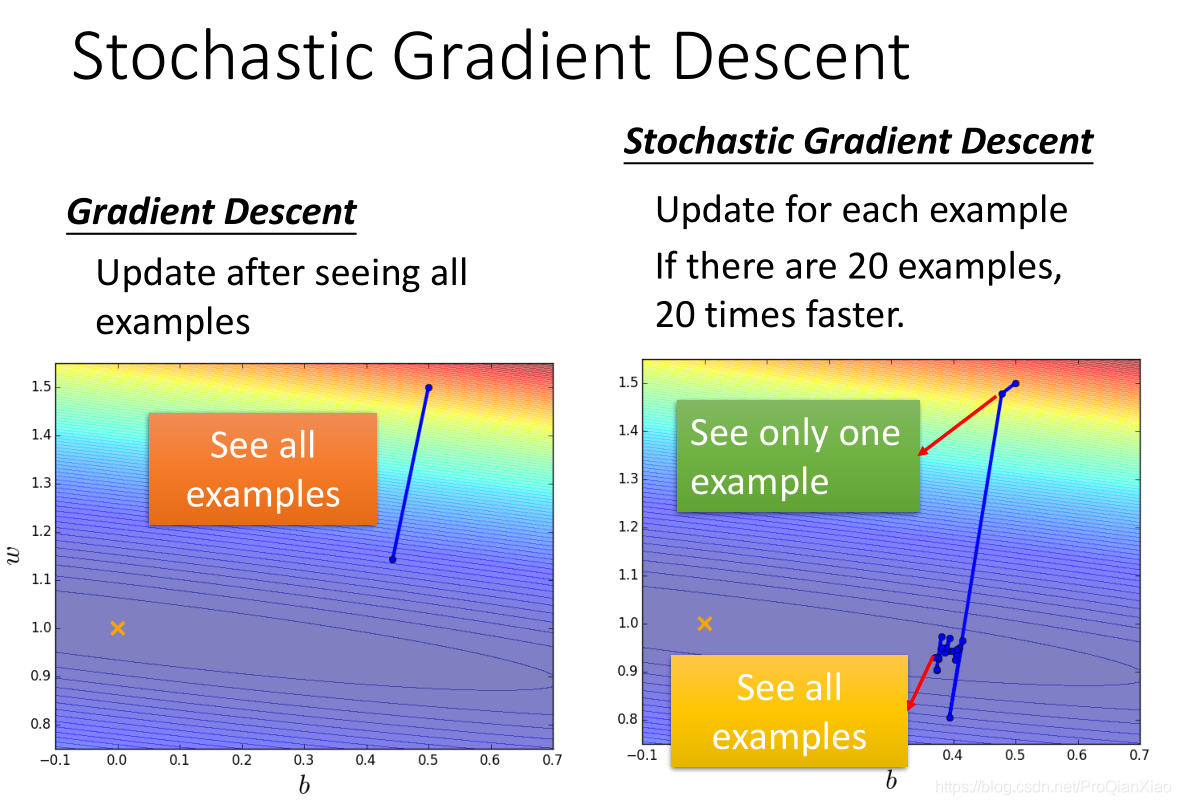 之前梯度下降算法中,Loss函数是对所有训练样本的Loss之和,而在随机梯度下降中,每次只采样一个样本,根据这一个样本进行一次梯度下降,所以随机梯度下降算法更新参数的过程更快。
之前梯度下降算法中,Loss函数是对所有训练样本的Loss之和,而在随机梯度下降中,每次只采样一个样本,根据这一个样本进行一次梯度下降,所以随机梯度下降算法更新参数的过程更快。
随机梯度下降(SGD, Stochastic Gradient Descent)是一种用于优化机器学习模型参数的算法,特别适用于大规模数据集的训练。SGD与传统的批量梯度下降(Batch Gradient Descent)不同,它在每次迭代中仅使用一个样本或一个小批量的样本(mini-batch)来计算梯度和更新参数。这种方法具有较快的更新速度和更好的内存效率,特别是在处理大数据集时。
优势
- 快速收敛:由于每次迭代只使用一个样本或小批量样本,更新频繁,收敛速度快。
- 内存效率:每次只需要加载一个样本或小批量样本,内存占用低,适合处理大规模数据集。
- 逃离局部最优:由于引入了随机性,SGD有助于跳出局部最优解,更容易找到全局最优解。
局限性
- 收敛波动:由于每次更新基于单个样本或小批量样本,导致参数更新不稳定,损失函数可能会剧烈波动。
- 调参困难:学习率的选择对SGD的性能影响很大,通常需要进行超参数调优。
改进方法
为了解决SGD的一些局限性,提出了多种改进算法,如:
- Mini-batch SGD:在每次迭代中使用一个小批量样本,而不是单个样本,平衡了收敛速度和稳定性。
- 动量(Momentum):在参数更新时引入动量项,利用之前梯度的指数加权平均来加速收敛。
- RMSprop:自适应调整学习率,缓解学习率逐渐减小的问题。
- Adam:结合了动量和RMSprop的优点,自适应地调整学习率。
应用场景
SGD广泛应用于深度学习和机器学习的各种模型训练中,包括神经网络、线性回归、逻辑回归等。它特别适用于大规模数据集和在线学习场景。
总结来说,SGD通过随机选择样本来进行参数更新,提供了快速且内存高效的优化方法,但其波动性和学习率调优是需要注意的问题。改进的变种算法如Mini-batch SGD、动量、RMSprop和Adam在实践中被广泛采用,以提高SGD的性能和稳定性。
三、特征缩放(Feature Scaling)
特征缩放是用来标准化数据特征的范围,减少特征中特异值的影响。
例如: 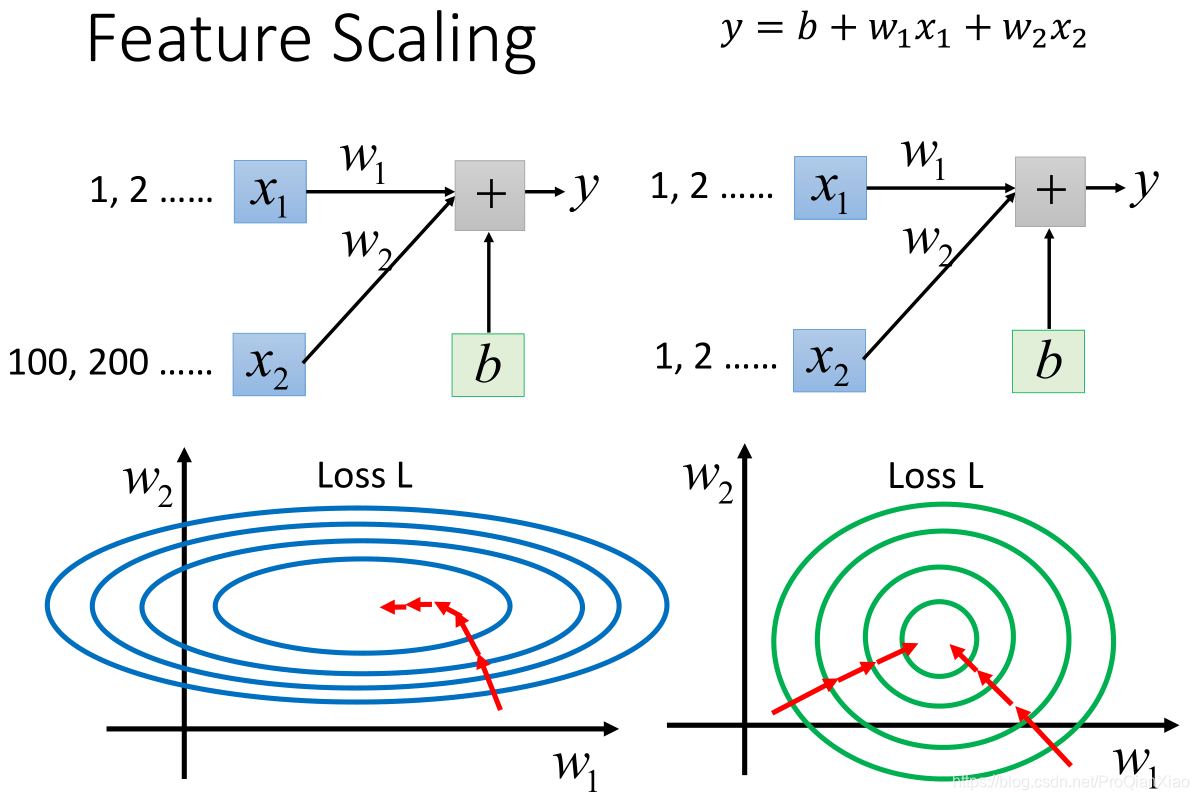


k-means聚类
K-means 是我们最常用的基于欧式距离的聚类算法,其认为两个目标的距离越近,相似度越大。
K-means 有一个著名的解释:牧师—村民模型:
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。 听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。 牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点…… 就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
我们可以看到该牧师的目的是为了让每个村民到其最近中心点的距离和最小。
1.2 算法步骤

1.3 复杂度
我们先看下伪代码:
1 | 获取数据 n 个 m 维的数据 |

2. 优缺点
2.1 优点
- 容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了;
- 处理大数据集的时候,该算法可以保证较好的伸缩性;
- 当簇近似高斯分布的时候,效果非常不错;
- 算法复杂度低。
2.2 缺点
- K 值需要人为设定,不同 K 值得到的结果不一样;
- 对初始的簇中心敏感,不同选取方式会得到不同结果;
- 对异常值敏感;
- 样本只能归为一类,不适合多分类任务;
- 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。
3. 算法调优与改进
针对 K-means 算法的缺点,我们可以有很多种调优方式:如数据预处理(去除异常点),合理选择 K 值,高维映射等。以下将简单介绍:
3.1 数据预处理
K-means 的本质是基于欧式距离的数据划分算法,均值和方差大的维度将对数据的聚类产生决定性影响。所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的。常见的数据预处理方式有:数据归一化,数据标准化。
此外,离群点或者噪声数据会对均值产生较大的影响,导致中心偏移,因此我们还需要对数据进行异常点检测。
3.2 合理选择 K 值
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点,常见的选取 K 值的方法有:手肘法、Gap statistic 方法。
手肘法:
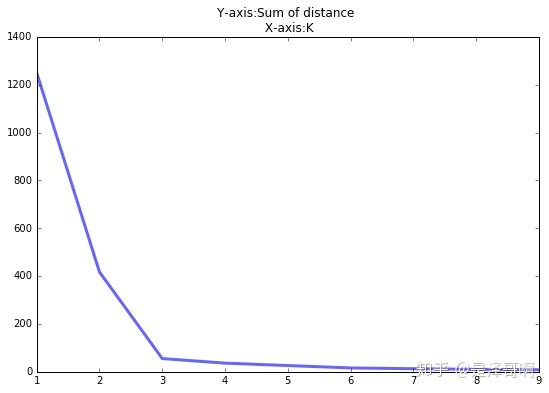
当 K < 3 时,曲线急速下降;当 K > 3 时,曲线趋于平稳,通过手肘法我们认为拐点 3 为 K 的最佳值。
手肘法的缺点在于需要人工看不够自动化,所以我们又有了 Gap statistic 方法,这个方法出自斯坦福大学的几个学者的论文:Estimating the number of clusters in a data set via the gap statistic
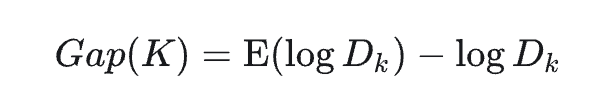

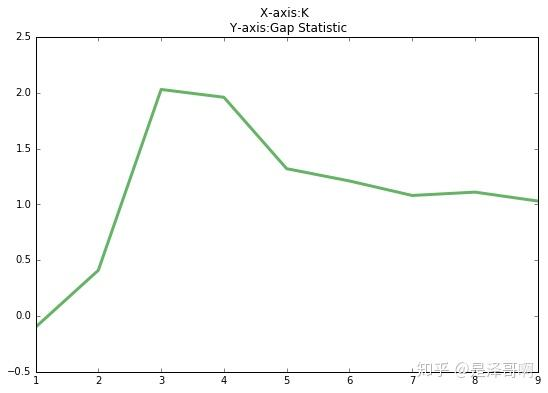
由图可见,当 K=3 时,Gap(K) 取值最大,所以最佳的簇数是 K=3。
Github 上一个项目叫 gap_statistic ,可以更方便的获取建议的类簇个数。
3.3 采用核函数
基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 K-means 算法,是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
3.4 K-means++
我们知道初始值的选取对结果的影响很大,对初始值选择的改进是很重要的一部分。在所有的改进算法中,K-means++ 最有名。
K-means++ 算法步骤如下所示:

简单的来说,就是 K-means++ 就是选择离已选中心点最远的点。这也比较符合常理,聚类中心当然是互相离得越远越好。

3.5 ISODATA
ISODATA 的全称是迭代自组织数据分析法。它解决了 K 的值需要预先人为的确定这一缺点。而当遇到高维度、海量的数据集时,人们往往很难准确地估计出 K 的大小。ISODATA 就是针对这个问题进行了改进,它的思想也很直观:当属于某个类别的样本数过少时把这个类别去除,当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。
4. 收敛证明
我们先来看一下 K-means 算法的步骤:先随机选择初始节点,然后计算每个样本所属类别,然后通过类别再跟新初始化节点。这个过程有没有想到之前介绍的 EM 算法 。
我们需要知道的是 K-means 聚类的迭代算法实际上是 EM 算法。EM
算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题。在
K-means 中的隐变量是每个类别所属类别。K-means 算法迭代步骤中的
每次确认中心点以后重新进行标记 对应 EM 算法中的 E 步
求当前参数条件下的 Expectation 。而
根据标记重新求中心点 对应 EM 算法中的 M 步
求似然函数最大化时(损失函数最小时)对应的参数 。
首先我们看一下损失函数的形式:

调参

多任务 loss 协调
基于经验自己配置,或者基于现有的论文
一般按照两个原则
1.各个loss的数量级保持一致
2.各个loss单独作用的时候梯度的模长的数量级保持一致
这两个原则二选一即可


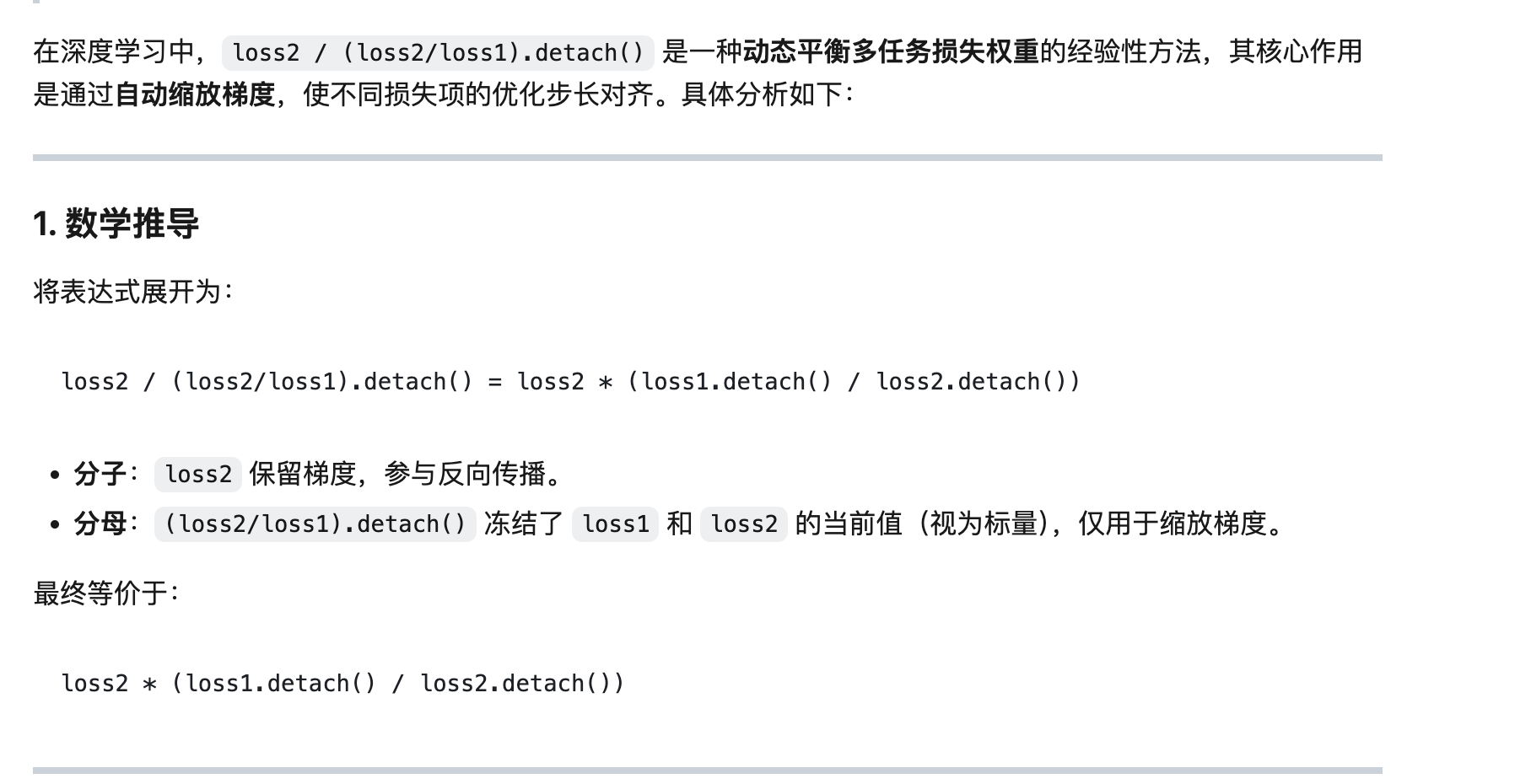

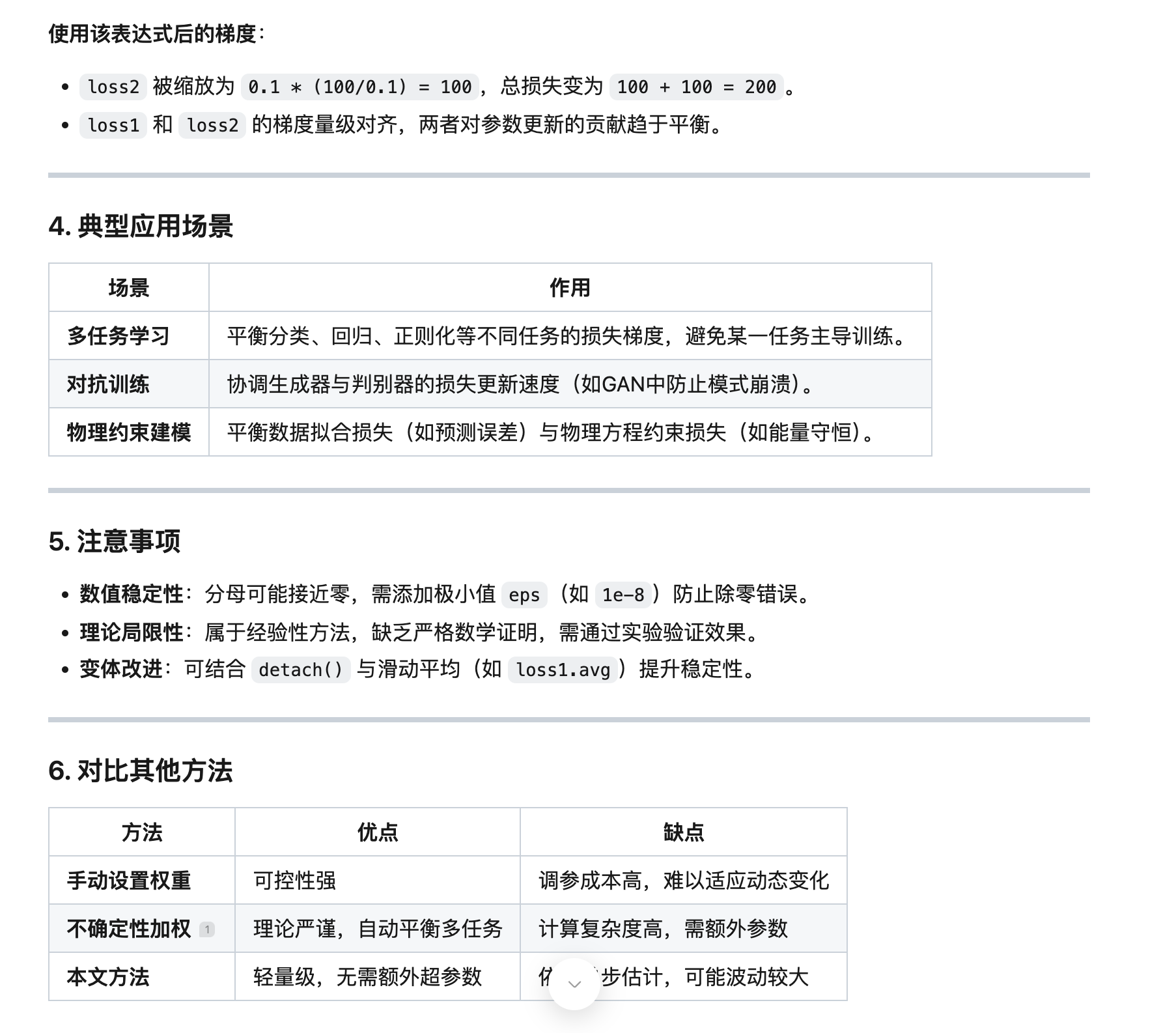

1 | # 原始表达式(存在除零风险) |
完整代码示例(PyTorch)
1 | import torch |

总结神经网络训练不收敛或训练失败的原因

数据平衡问题
https://www.zhihu.com/question/654186093/answer/3483543427
https://zhuanlan.zhihu.com/p/86891438


https://link.zhihu.com/?target=https%3A//github.com/ZhiningLiu1998/imbalanced-ensemble
https://github.com/ZhiningLiu1998/imbalanced-ensemble


注意这句话


batch_size
batch_size越大训练时间越少,
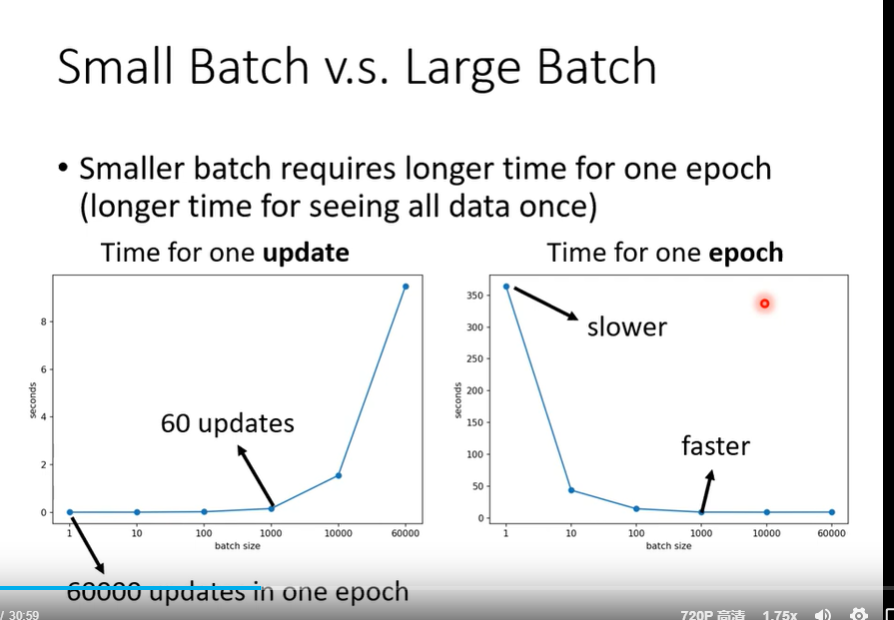
但是太大的batch_SIZE会导致准确率降低,这个是optimization的问题
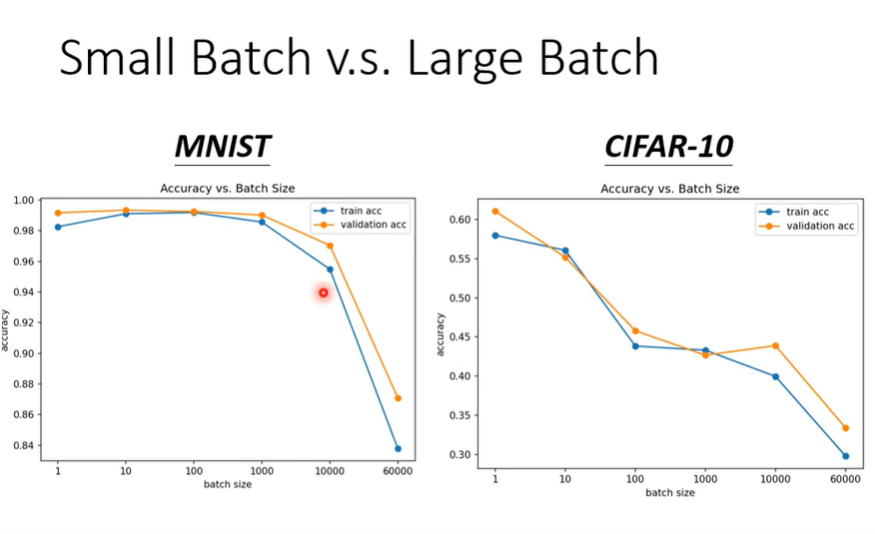

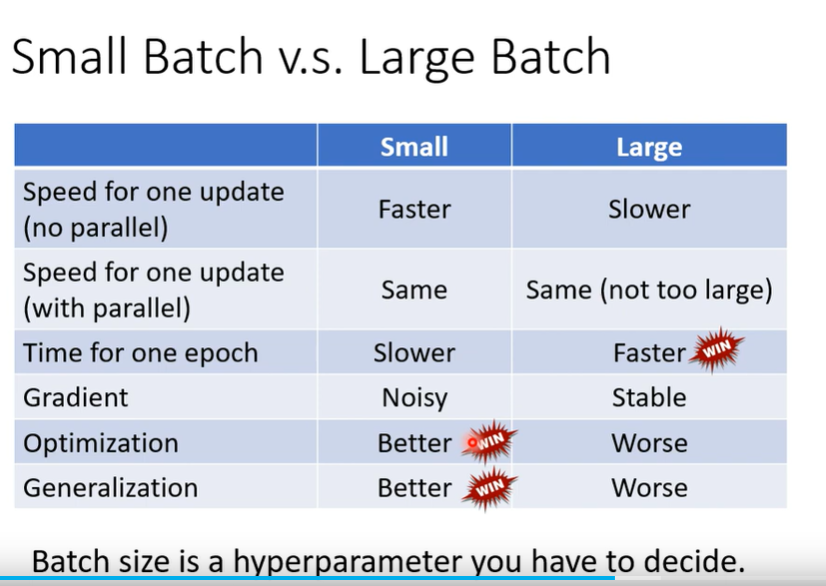
梯度上升和梯度下降的区别是什么?
!!!!!!! 简单来说就是正常的机器学习算法是需要计算loss函数的梯度,往梯度下降的方向走,需要loss函数的最小值
**但是梯度上升时,这个函数不是loss函数,而是一个真正的func函数,需要找这个func函数的最大值**梯度上升和梯度下降是两种相反的优化方法,主要区别如下:
目标方向:
梯度下降的目标是找到函数的最小值,因此沿着函数梯度的负方向更新参数。
梯度上升的目标是找到函数的最大值,所以沿着函数梯度的正方向更新参数。
更新参数的方式:
假设函数 f 关于参数 w 的梯度为
∇f(w) ,学习率为 α 。
在梯度下降中,参数的更新公式为:w = w - α * ∇f(w) 。
在梯度上升中,参数的更新公式为:w = w + α * ∇f(w) 。
应用场景:
梯度下降常用于损失函数的最小化,比如在机器学习中,通过最小化预测值与真实值之间的差异来优化模型的参数。
梯度上升则常用于需要最大化某个目标函数的情况,比如强化学习中最大化奖励,或者在某些特定的优化问题中找到使某个函数达到最大值的参数配置。
示例:
假设有一个简单的二次函数 f(w) = w^2 ,其梯度为
∇f(w) = 2w 。
如果使用梯度下降,学习率为 0.1 ,初始参数
w = 2 ,则第一次更新为
w = 2 - 0.1 * 2 * 2 = 1.6 。
如果使用梯度上升,同样学习率为 0.1 ,初始参数
w = 2 ,则第一次更新为
w = 2 + 0.1 * 2 * 2 = 2.4 。
总的来说,梯度上升和梯度下降的核心区别在于更新参数的方向,一个朝着梯度正方向,一个朝着梯度负方向,以分别实现最大化和最小化的目标。
理解使用生成式模型f(x)=sigmoid(wx+b) 进行二分类所蕴含的数学意义




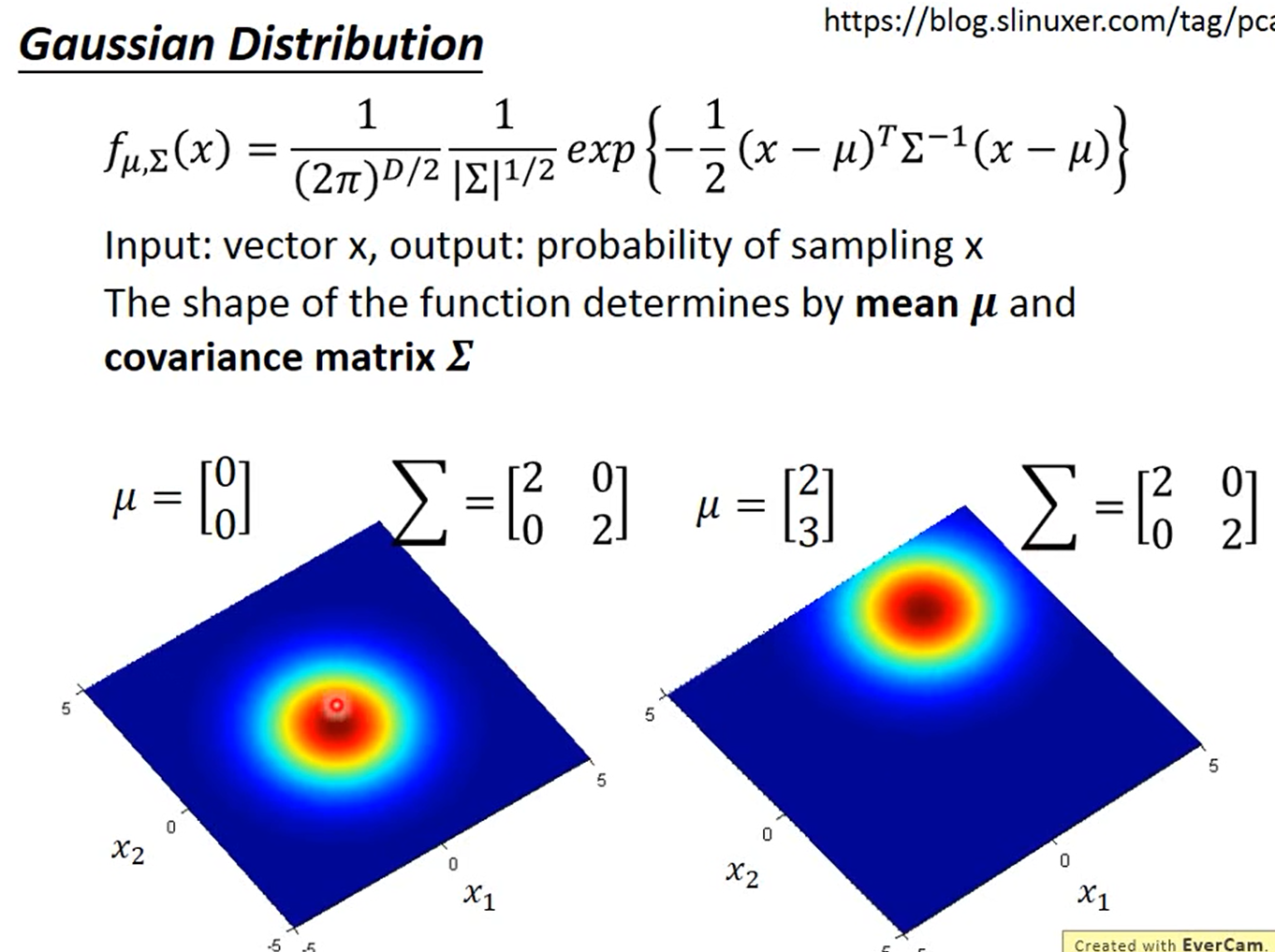


实际就是这里不用求两个高斯分布的参数’



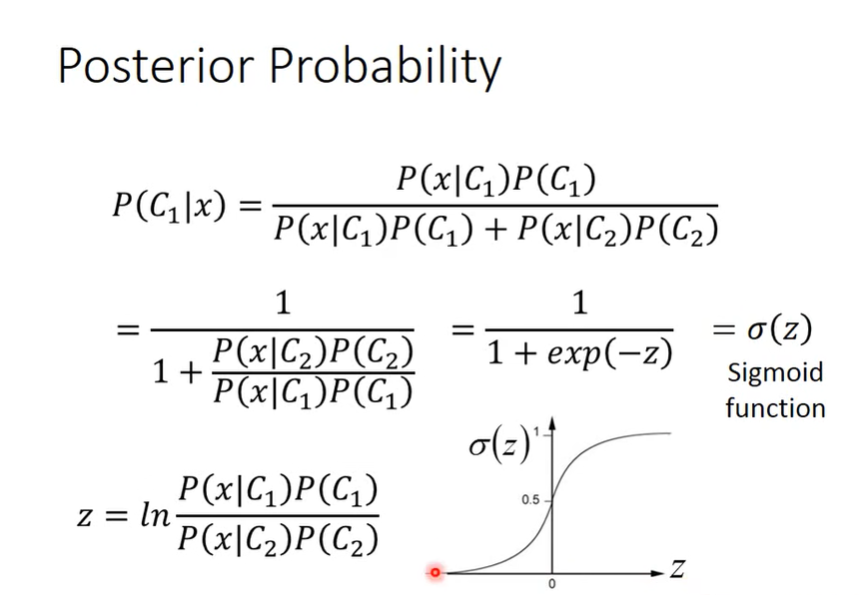
所以给定一个 x,属于C1类的概率就可以用sigmoid(w*x+b)来表示
用一张图形象展示判别模型和生成模型的区别
(要结合上面的知识点)
模型是一样的,但是生成模型不同训练样本找出来的模型参数(根据不同的假设找出不同的w和b)是不一样的,而判别模型是一样的

生成模型 :源头导向型,关注数据时如何生成的,然后再对一个信号进行分类。(信号输入时,生成模型判断哪个类别最有可能产生这个信号,则这个信号就属于哪个类别。
判别模型 :结果导向型,关注类别之间的差别,并不关心样本的数据时怎么生成的,根据样本之间的“分界线"来简单对给定的样本进行分类。

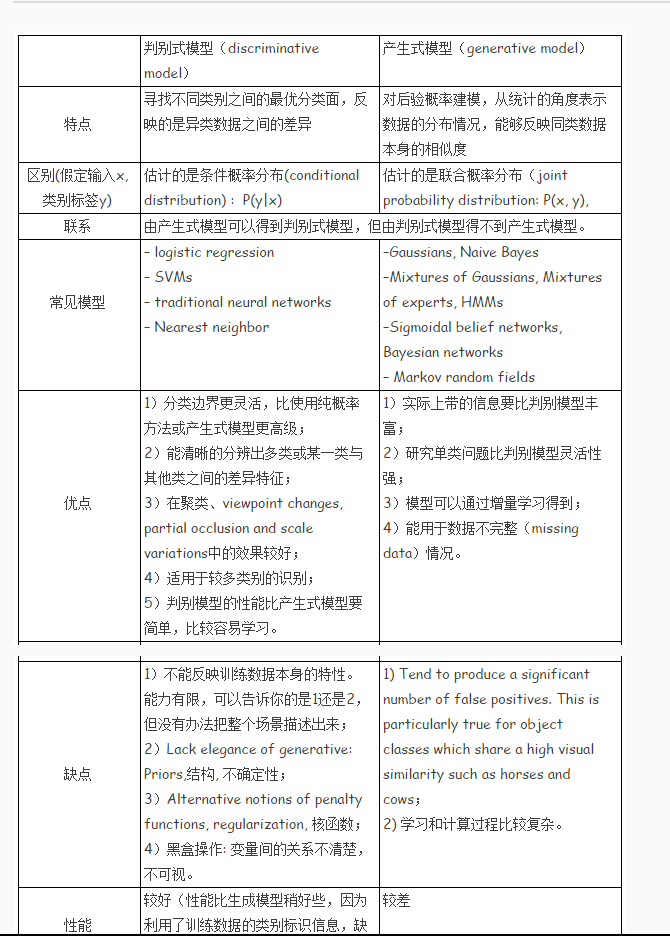
偏差和方差
这篇博客介绍机器学习中误差(error)的来源,知道我们的模型中产生的误差来自于哪一部分,才能更好地进行模型的调整。一般来说,误差的来源有两部分:偏差(bias)和方差(variance)。偏差和方差——用来衡量模型泛化能力的工具,所以我的理解是在测试集上面根据偏差和方差来对模型进行一个评估。
回顾之前回归问题中的例子,简单模型对于数据的拟合能力比较差,在训练集和测试集上面效果均不好;但同时不是越复杂的模型越好,因为有可能产生过拟合的现象,所以需要选择合适的模型。偏差-方差分析可以帮我们诊断模型中存在的问题(过于复杂或者过于简单)。
偏差就是:预测输出的期望值 - 真实值,(描述模型的拟合能力)
方差就是:(每个模型实例的预测输出 - 模型预测输出的期望值)^ 2 (描述模型的稳定性,即受数据扰动的影响程度)
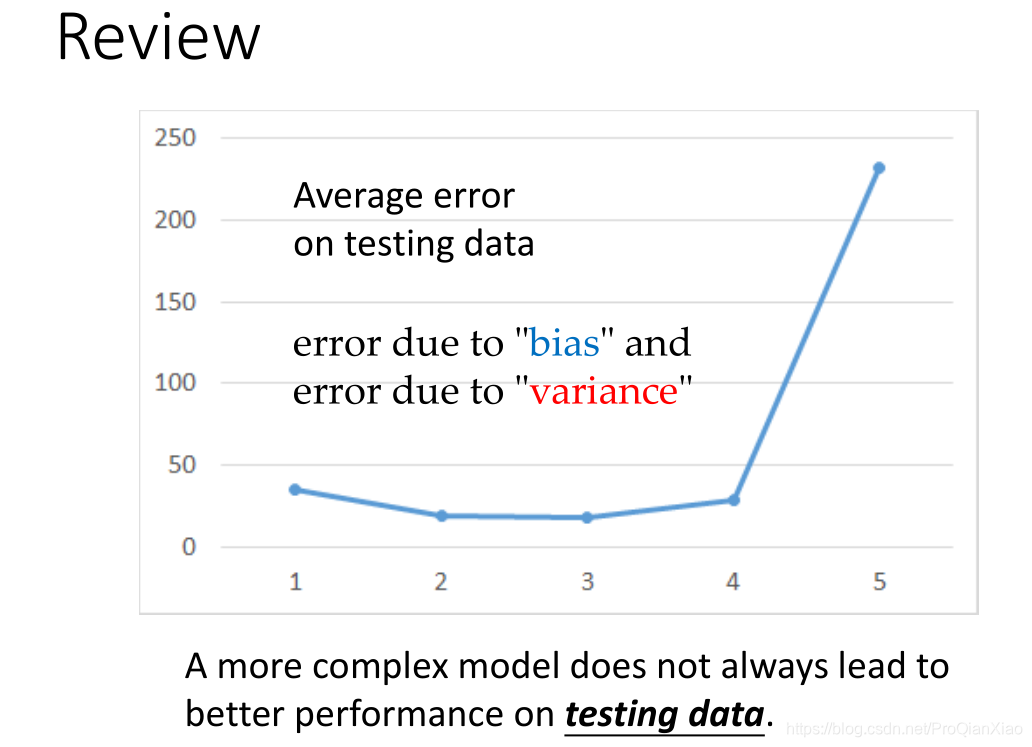
还是以宝可梦进化之后的CP值预测为例,如果我们有一些不同的训练数据(也就是李宏毅老师PPT中所说从若干个平行世界中收集的不同的宝可梦),

实质上是指有几个不同的训练集(TrainData_1,TrainData_2,TrainData_3),模型分别在不同的训练集上面训练,然后在同样的测试集(TestData)上面测试。对于不同的训练集,我们会得到一个模型的实例,比如有一次模型和五次模型,训练结果:(这里,“模型”表示具体的模型类别(比如一次模型,二次模型);“模型实例”表示一个模型在不同训练集上面训练得到的最终模型,有几个训练集就会有几个模型实例。)
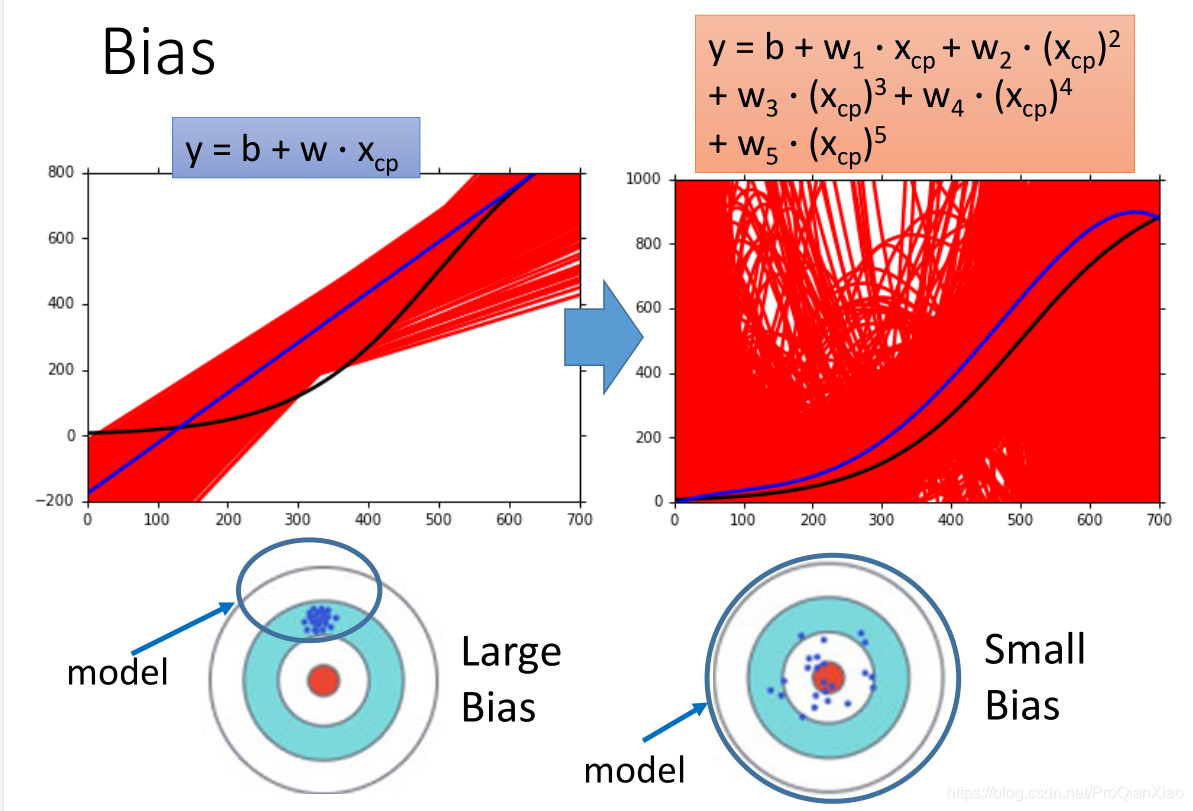
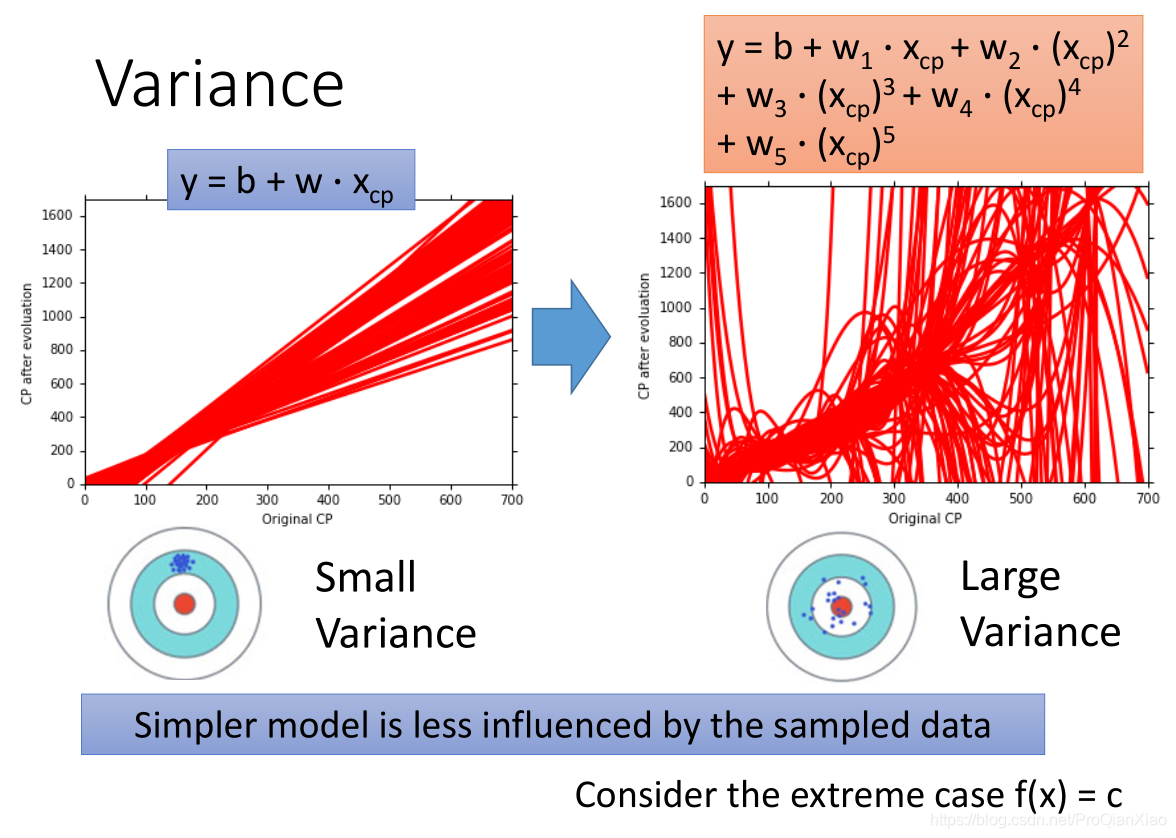
图片中,红色线表示在100个不同的训练集上面得到的模型的实例,蓝色线表示模型的预测输出的期望,黑色线是真实值。
可以看出,一次模型的偏差较大,方差较小;五次模型的偏差较小,方差较大。
数学定义
上面是偏差和方差一个比较直观的理解,接下来给出数学形式的定义:

偏差-方差与模型复杂度
偏差和方差的几种情况: 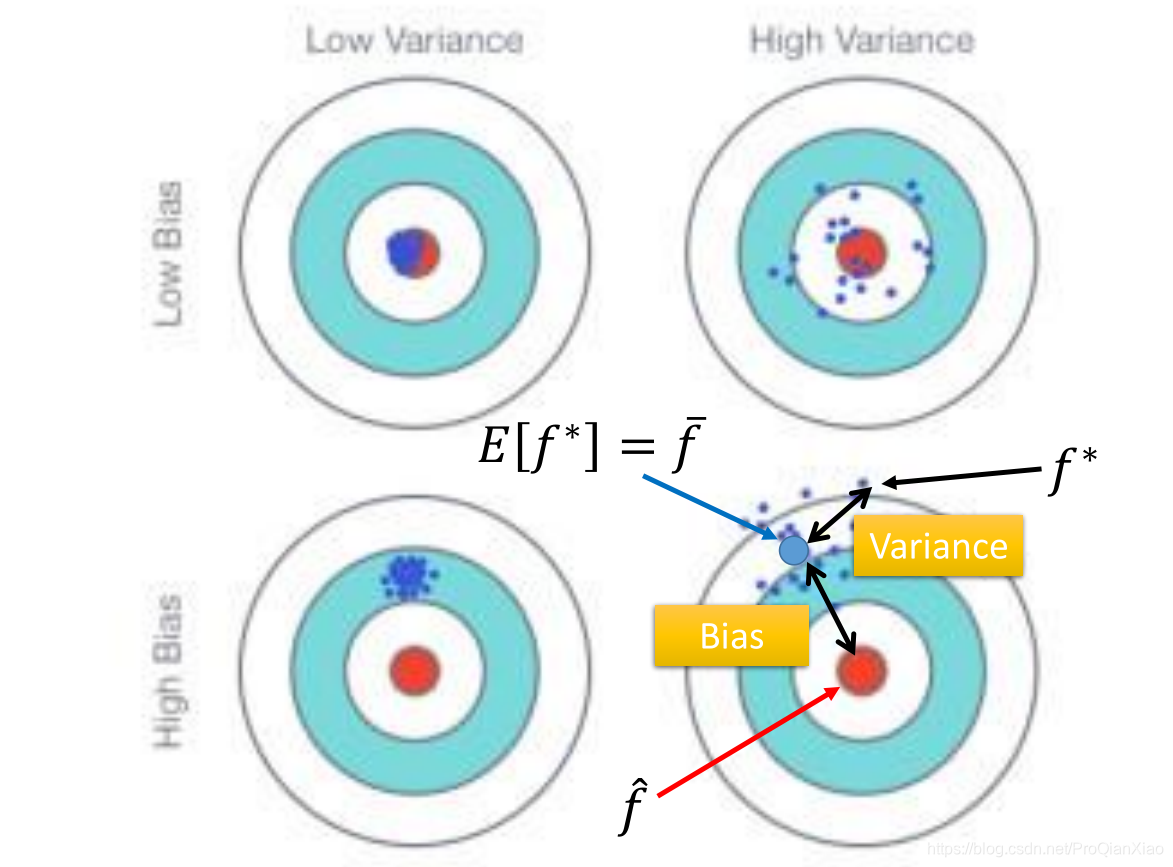
偏差小,方差小:追求的目标,理想的模型。 偏差小,方差大:模型比较复杂,在训练集上面过拟合,导致在测试集上面泛化效果不好。 偏差大,方差小:模型比较简单,拟合能力较差,在训练集上面欠拟合,导致在测试集上面泛化效果不好。 偏差大,方差大:最糟的情况,模型需要重新进行设计,不适合于现有数据集。
很直观的一个解释,因为偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力,所以偏差大的模型拟合能力差,模型简单,容易欠拟合;方差度量数据扰动所造成的影响(在不同的训练集上面训练得到的模型在测试集上面效果表现相差很大),说明模型过于拟合训练集,模型复杂。
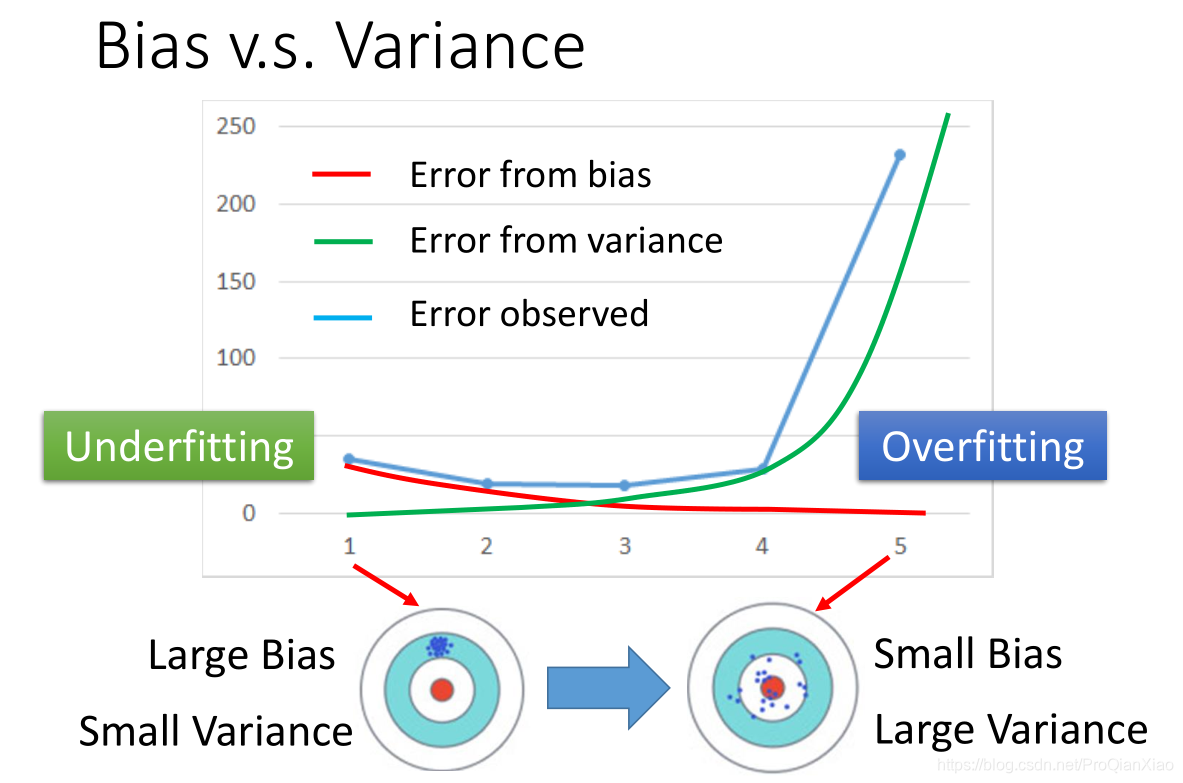
调整方法
综上,根据模型在测试集上的表现,可以得出结论:
偏差大,方差小:模型欠拟合
偏差小,方差大:模型过拟合
对于偏差大(欠拟合)的情况,常用的解决方法:
• 重新设计模型,使用更复杂的模型结构
• 输入中使用更多的特征
对于方差大(过拟合)的情况,常用的解决方法:
• 参数正则化(减小模型的复杂程度)
• 使用更多的训练数据
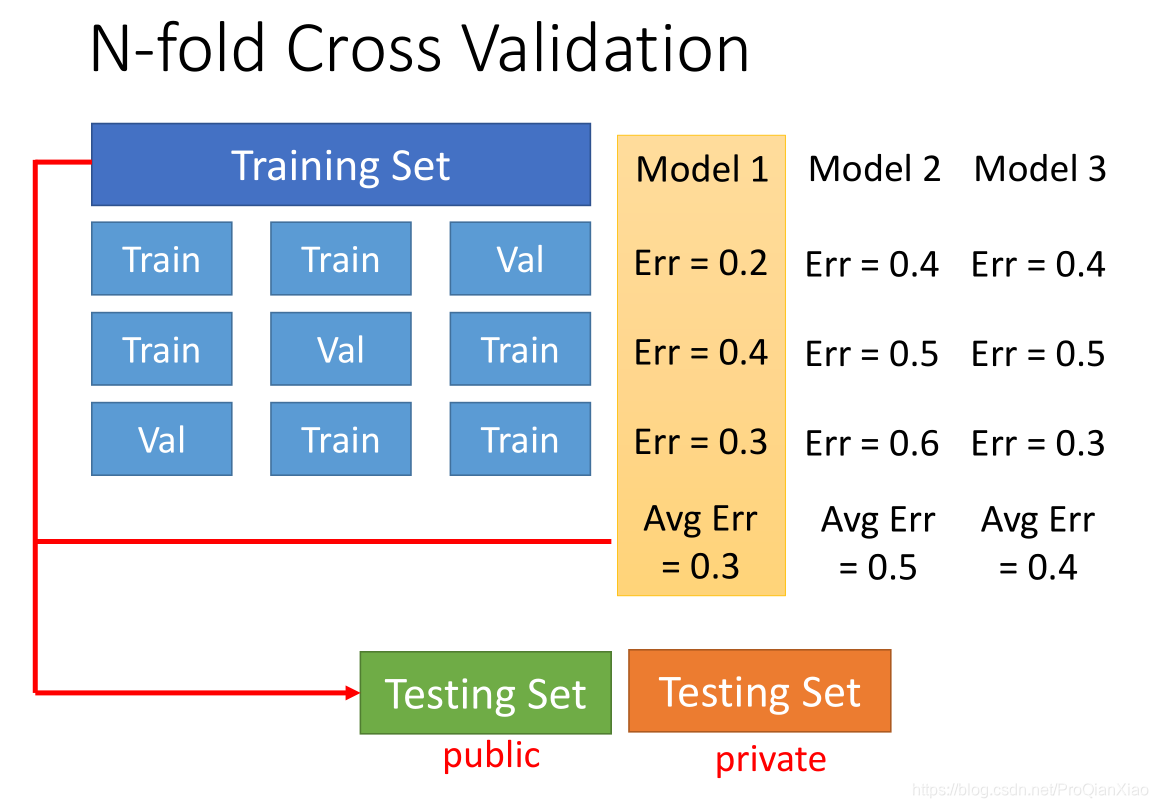
K-折交叉验证
模型的设计选择需要在偏差和方差之间进行平衡,在选择合适的模型(比如一次模型还是二次模型)时,常用的方法是进行K-折交叉验证。将训练集的数据等分成K份,每次使用(K-1)份数据进行训练,余下的1份数据进行验证,进行K次,保证每份数据均做过验证集,统计K次验证集上面的loss,取loss均值最小的模型作为使用的模型。
softmax
主要用途:
softmax是深度学习任务中常用于计算最终输出类别的函数。
Softmax 函数主要用于多分类问题中,将多个神经元的输出值转换为概率分布。
Softmax 函数在很多机器学习任务中都有广泛的应用,比如图像分类、文本分类等,它有助于将模型的输出转化为可解释的类别概率。

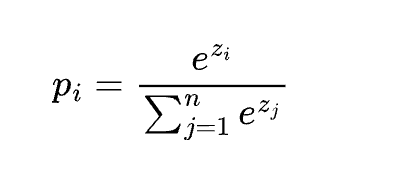
- softmax和我们普通意义上的max函数不同,每一个元素都有一个概率,而不是其中一个元素为1,其余为0。它的含义是对于输入向量,有多大的概率去选择元素1、元素2、元素3等,主要的目的是使得概率计算过程可导。
以下是对 Softmax 函数的一些关键理解点:
- 输出值在 0 到 1 之间:Softmax 函数确保每个输出值都在 0 和 1 之间。
- 输出值总和为 1:所有输出值的总和为 1,这使得它们可以被解释为概率。
- 强调相对大小:Softmax 函数会放大输入值之间的差异。较大的输入值在经过 Softmax 计算后会得到更大的概率值,较小的输入值则会得到较小的概率值。
例如,假设有一个神经网络的输出为 [1, 2, 0],经过 Softmax
函数计算后,得到的概率分布可能是
[0.269, 0.731, 0.0]。这意味着模型预测第二个类别是最有可能的,第一个类别有一定的可能性,而第三个类别几乎不可能。
全连接层(Fully Connected Layer)
全连接层(Fully Connected Layer),也称为密集层(Dense Layer),是一种在深度学习中广泛使用的神经网络层。
全连接层在整个网络卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话, 全连接层则起到将学到的特征表示映射到样本的标记空间的作用 。
在 CNN 中,全连接常出现在最后几层,用于对前面设计的特征做加权和。比如 mnist,前面的卷积和池化相当于做特征工程,后面的全连接相当于做特征加权。(卷积相当于全连接的有意弱化,按照局部视野的启发,把局部之外的弱影响直接抹为零影响;还做了一点强制,不同的局部所使用的参数居然一致。弱化使参数变少,节省计算量,又专攻局部不贪多求全;强制进一步减少参数。少即是多) 在 RNN 中,全连接用来把 embedding 空间拉到隐层空间,把隐层空间转回 label 空间等。
一段来自知乎的通俗理解:
从卷积网络谈起,卷积网络在形式上有一点点像咱们正在召开的“人民代表大会”。卷积核的个数相当于候选人,图像中不同的特征会激活不同的“候选人”(卷积核)。池化层(仅指最大池化)起着类似于“合票”的作用,不同特征在对不同的“候选人”有着各自的喜好。
全连接相当于是“代表普选”。所有被各个区域选出的代表,对最终结果进行“投票”,全连接保证了receiptive field 是整个图像,既图像中各个部分(所谓所有代表),都有对最终结果影响的权利。
在实际使用中,全连接层可由卷积操作实现 :对前层是全连接的全连接层可以转换为卷积核为1*1的卷积;而前层是卷积层的全连接层可以转换为卷积核为前层卷积输出结果的高和宽一样大小的全局卷积。
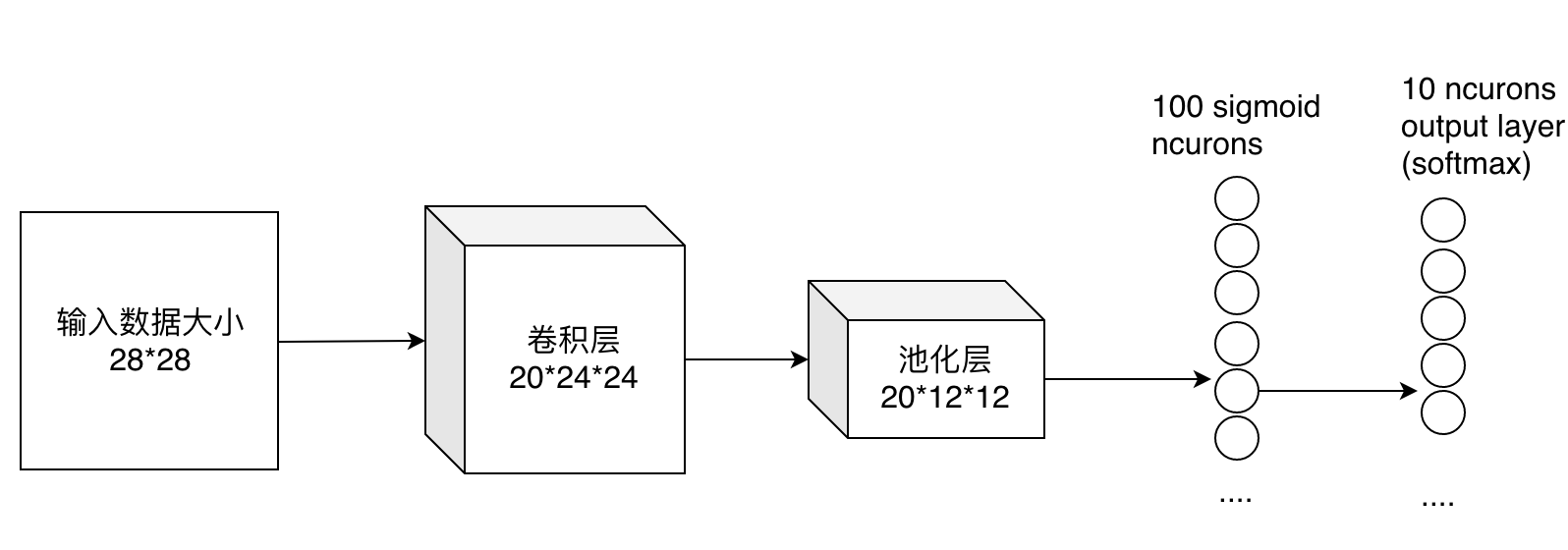
最后的两列小圆球就是两个全连接层,在最后一层卷积结束后,进行了最后一次池化,输出了20个12*12的图像,然后通过了一个全连接层变成了1*100的向量。
这是怎么做到的呢,其实就是 有20*100个12*12的不同卷积核卷积出来的 ,我们也可以这样想,就是 每个神经元的输出是12*12*20个输入值与对应的权值乘积的和 。对于输入的 每一张图,用了一个和图像一样大小的核卷积,这样整幅图就变成了一个数了 ,如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。
一、结构与原理
全连接层中的每个神经元都与上一层的所有神经元相连接。这意味着如果上一层有\(n\)个神经元,那么全连接层中的每个神经元都有\(n\)个输入权重。
在全连接层中,输入数据通常是一个一维向量,它是通过将上一层的多维特征图展平得到的。每个神经元对输入向量进行加权求和,并通过一个激活函数得到输出。
数学表达式可以表示为:\(y = f(Wx + b)\),其中\(x\)是输入向量,\(W\)是权重矩阵,\(b\)是偏置项,\(f(\cdot)\)是激活函数,\(y\)是输出。
它是怎么样把3x3x5的输出,转换成1x4096的形式
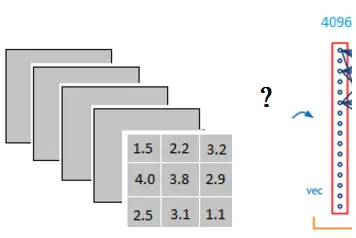
很简单,可以理解为在中间做了一个卷积 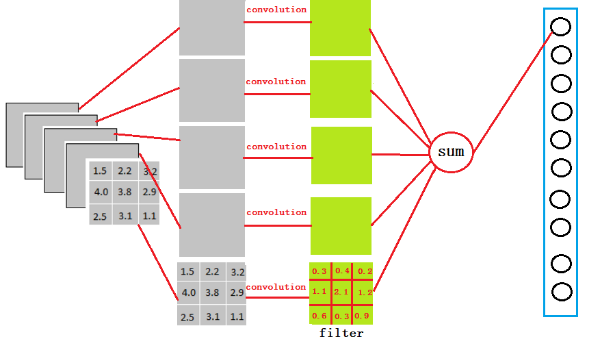
从上图我们可以看出,我们用一个3x3x5的filter 去卷积激活函数的输出,得到的结果就是一个fully connected layer 的一个神经元的输出,这个输出就是一个值
因为我们有4096个神经元
我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出
以VGG-16再举个例子吧
再VGG-16全连接层中
对224x224x3的输入,最后一层卷积可得输出为7x7x512,如后层是一层含4096个神经元的FC,则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程。
很多人看到这,可能就恍然大悟
哦,我懂了,就是做个卷积呗
不
你不懂
这一步卷积一个非常重要的作用
就是把分布式特征representation映射到样本标记空间
什么,听不懂
那我说人话
就是它把特征representation整合到一起,输出为一个值
这样做,有一个什么好处?
就是大大减少特征位置对分类带来的影响
来,让我来举个简单的例子 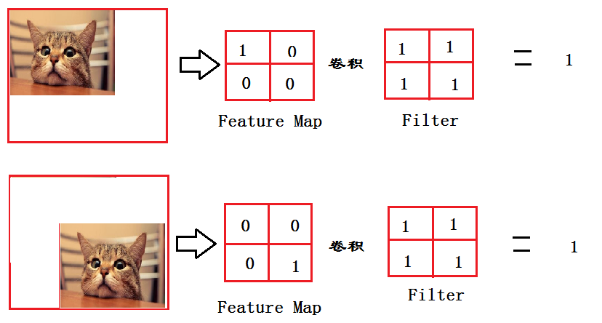
这个例子可能过于简单了点
可是我懒得画了,大家将就着看吧
从上图我们可以看出,猫在不同的位置,输出的feature值相同,但是位置不同
对于电脑来说,特征值相同,但是特征值位置不同,那分类结果也可能不一样
而这时全连接层filter的作用就相当于
喵在哪我不管
我只要喵
于是我让filter去把这个喵找到
实际就是把feature map 整合成一个值
这个值大
哦,有喵
这个值小
那就可能没喵
和这个喵在哪关系不大了有没有
鲁棒性有大大增强了有没有
喵喵喵
因为空间结构特性被忽略了,所以全连接层不适合用于在方位上找Pattern的任务,比如segmentation
ok, 我们突然发现全连接层有两层1x4096fully connected layer平铺结构(有些网络结构有一层的,或者二层以上的)
好吧也不是突然发现,我只是想增加一点戏剧效果 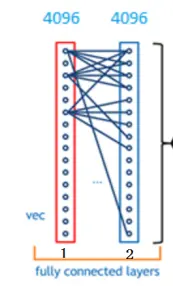
但是大部分是两层以上呢
这是为啥子呢
泰勒公式都知道吧
意思就是用多项式函数去拟合光滑函数
我们这里的全连接层中一层的一个神经元就可以看成一个多项式
我们用许多神经元去拟合数据分布
但是只用一层fully connected layer 有时候没法解决非线性问题
而如果有两层或以上fully connected layer就可以很好地解决非线性问题了
说了这么多,我猜你应该懂的
听不懂?
那我换个方式给你讲
我们都知道,全连接层之前的作用是提取特征
全理解层的作用是分类
我们现在的任务是去区别一图片是不是猫

假设这个神经网络模型已经训练完了
全连接层已经知道
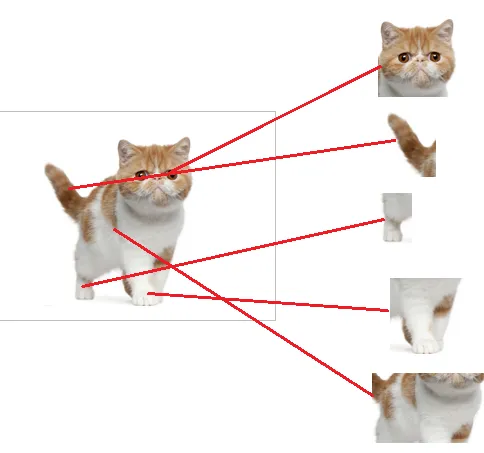
当我们得到以上特征,我就可以判断这个东东是猫了
因为全连接层的作用主要就是实现分类(Classification)
从下图,我们可以看出 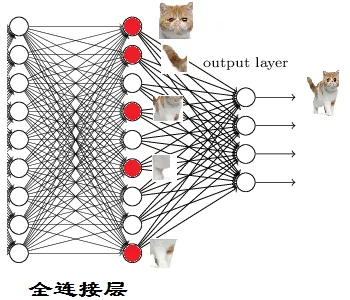
红色的神经元表示这个特征被找到了(激活了)
同一层的其他神经元,要么猫的特征不明显,要么没找到
当我们把这些找到的特征组合在一起,发现最符合要求的是猫
ok,我认为这是猫了
那我们现在往前走一层
那们现在要对子特征分类,也就是对猫头,猫尾巴,猫腿等进行分类
比如我们现在要把猫头找出来 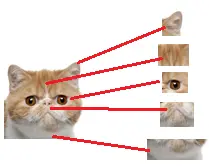
猫头有这么些个特征
于是我们下一步的任务
就是把猫头的这么些子特征找到,比如眼睛啊,耳朵啊 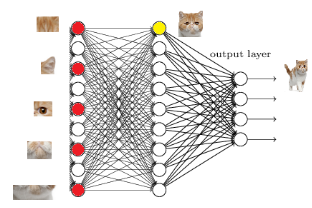
道理和区别猫一样
当我们找到这些特征,神经元就被激活了(上图红色圆圈)
这细节特征又是怎么来的?
就是从前面的卷积层,下采样层来的
至此,关于全连接层的信息就简单介绍完了
全连接层参数特多(可占整个网络参数80%左右),近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化(global average pooling,GAP)取代全连接层来融合学到的深度特征
需要指出的是,用GAP替代FC的网络通常有较好的预测性能
于是还出现了
[1411.4038] Fully Convolutional Networks for Semantic Segmentationarxiv.org/abs/1411.4038
以后会慢慢介绍的
.
.
.
二、作用
- 特征融合与变换
- 全连接层可以将上一层学习到的局部特征进行融合和变换,提取更高级别的全局特征。通过调整权重和偏置,全连接层可以学习到不同特征之间的复杂关系。
- 分类与回归
- 在神经网络的最后几层,全连接层通常用于分类或回归任务。通过将学习到的特征映射到输出类别或数值,全连接层可以对输入数据进行预测。
三、特点
- 参数数量多
- 由于全连接层中的每个神经元都与上一层的所有神经元相连接,因此全连接层通常具有大量的参数。这使得全连接层在训练过程中需要大量的计算资源和数据,并且容易过拟合。
- 可解释性差
- 全连接层中的权重和偏置通常难以解释,因为它们是通过复杂的优化过程学习得到的。这使得全连接层在一些需要可解释性的应用中受到限制。
四、应用场景
- 图像分类
- 在图像分类任务中,全连接层通常用于将卷积神经网络学习到的图像特征映射到不同的类别。例如,在ResNet等经典的图像分类网络中,最后几层通常是全连接层。
- 自然语言处理
- 在自然语言处理任务中,全连接层可以用于将词向量或句子向量映射到不同的语义类别或情感标签。例如,在文本分类、情感分析等任务中,全连接层通常是神经网络的最后几层。
- 语音识别
- 在语音识别任务中,全连接层可以用于将声学特征映射到不同的音素或单词。例如,在深度神经网络语音识别系统中,全连接层通常用于将学习到的声学特征进行分类。
嵌入(embedding)层的理解
embedding层作用:①降维②对低维的数据进行升维时,可能把一些其他特征给放大了,或者把笼统的特征给分开了。
Embedding其实就是一个映射,从原先所属的空间映射到新的多维空间中,也就是把原先所在空间嵌入到一个新的空间中去。
嵌入层的一个作用——降维
首先,我们有一个one-hot编码的概念。
假设,我们中文,一共只有10个字。。。只是假设啊,那么我们用0-9就可以表示完
比如,这十个字就是“我从哪里来,要到何处去”
其分别对应“0-9”,如下:
我 从 哪 里 来 要 到 何 处 去
0 1 2 3 4 5 6 7 8 9
那么,其实我们只用一个列表就能表示所有的对话
如:我 从 哪 里 来 要 到 何 处 去 ——>>>[0 1 2 3 4 5 6 7 8 9]
或:我 从 何 处 来 要 到 哪 里 去 ——>>>[0 1 7 8 4 5 6 2 3 9]
但是,我们看看one-hot编码方式(详见:https://blog.csdn.net/tengyuan93/article/details/78930285)
他把上面的编码方式弄成这样
--我从哪里来,要到何处去
[ [1 0 0 0 0 0 0 0 0 0] [0 1 0 0 0 0 0 0 0 0] [0 0 1 0 0 0 0 0 0 0] [0 0 0 1 0 0 0 0 0 0] [0 0 0 0 1 0 0 0 0 0] [0 0 0 0 0 1 0 0 0 0] [0 0 0 0 0 0 1 0 0 0] [0 0 0 0 0 0 0 1 0 0] [0 0 0 0 0 0 0 0 1 0] [0 0 0 0 0 0 0 0 0 1]]
--我从何处来,要到哪里去
[ [1 0 0 0 0 0 0 0 0 0] [0 1 0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 1 0 0] [0 0 0 0 0 0 0 0 1 0] [0 0 0 0 1 0 0 0 0 0] [0 0 0 0 0 1 0 0 0 0] [0 0 0 0 0 0 1 0 0 0] [0 0 1 0 0 0 0 0 0 0] [0 0 0 1 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0 1]] 即:把每一个字都对应成一个十个(样本总数/字总数)元素的数组/列表,其中每一个字都用唯一对应的数组/列表对应,数组/列表的唯一性用1表示。如上,“我”表示成[1。。。。],“去”表示成[。。。。1],这样就把每一系列的文本整合成一个稀疏矩阵。
那问题来了,稀疏矩阵(二维)和列表(一维)相比,有什么优势。
很明显,计算简单嘛,稀疏矩阵做矩阵计算的时候,只需要把1对应位置的数相乘求和就行,也许你心算都能算出来;而一维列表,你能很快算出来?何况这个列表还是一行,如果是100行、1000行和或1000列呢?
所以,one-hot编码的优势就体现出来了,计算方便快捷、表达能力强。
然而,缺点也随着来了。
比如:中文大大小小简体繁体常用不常用有十几万,然后一篇文章100W字,你要表示成100W X 10W的矩阵???
这是它最明显的缺点。过于稀疏时,过度占用资源。
比如:其实我们这篇文章,虽然100W字,但是其实我们整合起来,有99W字是重复的,只有1W字是完全不重复的。那我们用100W X 10W的岂不是白白浪费了99W X 10W的矩阵存储空间。
那怎么办???
这时,Embedding层横空出世。
接下来给大家看一张图 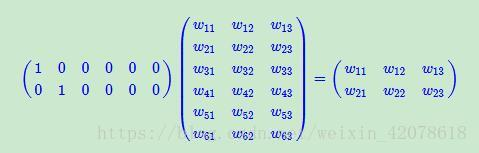
假设:我们有一个2 x 6的矩阵,然后乘上一个6 x 3的矩阵后,变成了一个2 x 3的矩阵。
先不管它什么意思,这个过程,我们把一个12个元素的矩阵变成6个元素的矩阵,直观上,大小是不是缩小了一半?
也许你已经想到了!!!对!!!不管你想的对不对,但是embedding层,在某种程度上,就是用来降维的,降维的原理就是矩阵乘法。在卷积网络中,可以理解为特殊全连接层操作,跟1x1卷积核异曲同工!!!484很神奇!!!
也就是说,假如我们有一个100W X10W的矩阵,用它乘上一个10W X 20的矩阵,我们可以把它降到100W X 20,瞬间量级降了。。。10W/20=5000倍!!!
这就是嵌入层的一个作用——降维。
然后中间那个10W X 20的矩阵,可以理解为查询表,也可以理解为映射表,也可以理解为过度表,whatever。
嵌入层的一个作用——升维
接着,既然可以降维,当然也可以升维。为什么要升维?------------可能把一些其他特征给放大了,或者把笼统的特征给分开了

这张图,我要你在10米开外找出五处不同!。。。What?烦请出题者走近两步,我先把我的刀拿出来,您再说一遍题目我没听清。
当然,目测这是不可能完成的。但是我让你在一米外,也许你一瞬间就发现衣服上有个心是不同的,然后再走近半米,你又发现左上角和右上角也是不同的。再走近20厘米,又发现耳朵也不同,最后,在距离屏幕10厘米的地方,终于发现第五个不同的地方在耳朵下面一点的云。
但是,其实无限靠近并不代表认知度就高了,比如,你只能距离屏幕1厘米远的地方找,找出五处不同。。。出题人你是不是脑袋被门挤了。。。
由此可见,距离的远近会影响我们的观察效果。同理也是一样的,
低维的数据可能包含的特征是非常笼统的,我们需要不停地拉近拉远来改变我们的感受野,让我们对这幅图有不同的观察点,找出我们要的茬。
embedding的又一个作用体现了。对低维的数据进行升维时,可能把一些其他特征给放大了,或者把笼统的特征给分开了。同时,这个embedding是一直在学习在优化的,就使得整个拉近拉远的过程慢慢形成一个良好的观察点。比如:我来回靠近和远离屏幕,发现45厘米是最佳观测点,这个距离能10秒就把5个不同点找出来了。
回想一下为什么CNN层数越深准确率越高,卷积层卷了又卷,池化层池了又升,升了又降,全连接层连了又连。因为我们也不知道它什么时候突然就学到了某个有用特征。但是不管怎样,学习都是好事,所以让机器多卷一卷,多连一连,反正错了多少我会用交叉熵告诉你,怎么做才是对的我会用梯度下降算法告诉你,只要给你时间,你迟早会学懂。因此,理论上,只要层数深,只要参数足够,NN能拟合任何特征。总之,它类似于虚拟出一个关系对当前数据进行映射。这个东西也许一言难尽吧,但是目前各位只需要知道它有这些功能的就行了。
接下来,继续假设我们有一句话,叫“公主很漂亮”,如果我们使用one-hot编码,可能得到的编码如下:
公 [0 0 0 0 1] 主 [0 0 0 1 0] 很 [0 0 1 0 0] 漂 [0 1 0 0 0] 亮 [1 0 0 0 0] 乍一眼看过似乎没毛病,其实本来人家也没毛病,或者假设咱们的词袋更大一些
公 [0 0 0 0 1 0 0 0 0 0] 主 [0 0 0 1 0 0 0 0 0 0] 很 [0 0 1 0 0 0 0 0 0 0] 漂 [0 1 0 0 0 0 0 0 0 0] 亮 [1 0 0 0 0 0 0 0 0 0] 假设吧,就假设咱们的词袋一共就10个字,则这一句话的编码如上所示。
这样的编码,最大的好处就是,不管你是什么字,我们都能在一个一维的数组里用01给你表示出来。并且不同的字绝对不一样,以致于一点重复都没有,表达本征的能力极强。
(缺陷)但是,因为其完全独立,其劣势就出来了。表达关联特征的能力几乎为0!!!
我给你举个例子,我们又有一句话“王妃很漂亮”
那么在这基础上,我们可以把这句话表示为
王 [0 0 0 0 0 0 0 0 0 1] 妃 [0 0 0 0 0 0 0 0 1 0] 很 [0 0 1 0 0 0 0 0 0 0] 漂 [0 1 0 0 0 0 0 0 0 0] 亮 [1 0 0 0 0 0 0 0 0 0] 从中文表示来看,我们一下就跟感觉到,王妃跟公主其实是有很大关系的,比如:公主是皇帝的女儿,王妃是皇帝的妃子,可以从“皇帝”这个词进行关联上;公主住在宫里,王妃住在宫里,可以从“宫里”这个词关联上;公主是女的,王妃也是女的,可以从“女”这个字关联上。
但是呢,我们用了one-hot编码,公主和王妃就变成了这样:
公 [0 0 0 0 1 0 0 0 0 0] 主 [0 0 0 1 0 0 0 0 0 0] 王 [0 0 0 0 0 0 0 0 0 1] 妃 [0 0 0 0 0 0 0 0 1 0] 你说,你要是不看前面的中文注解,你知道这四行向量有什么内部关系吗?看不出来,那怎么办?
既然,通过刚才的假设关联,我们关联出了“皇帝”、“宫里”和“女”三个词,那我们尝试这么去定义公主和王妃
公主一定是皇帝的女儿,我们假设她跟皇帝的关系相似度为1.0;公主从一出生就住在宫里,直到20岁才嫁到府上,活了80岁,我们假设她跟宫里的关系相似度为0.25;公主一定是女的,跟女的关系相似度为1.0;
王妃是皇帝的妃子,没有亲缘关系,但是有存在着某种关系,我们就假设她跟皇帝的关系相似度为0.6吧;妃子从20岁就住在宫里,活了80岁,我们假设她跟宫里的关系相似度为0.75;王妃一定是女的,跟女的关系相似度为1.0;
于是公主王妃四个字我们可以这么表示:
皇 宫 帝 里 女 公主 [ 1.0 0.25 1.0] 王妃 [ 0.6 0.75 1.0] 这样我们就把公主和王妃两个词,跟皇帝、宫里、女这几个字(特征)关联起来了,我们可以认为:
**公主=1.0 皇帝 +0.25宫里 +1.0*女**
**王妃=0.6 皇帝 +0.75宫里 +1.0*女**
或者这样,我们假设没歌词的每个字都是对等(注意:只是假设,为了方便解释):
皇 宫 帝 里 女 公 [ 0.5 0.125 0.5] 主 [ 0.5 0.125 0.5] 王 [ 0.3 0.375 0.5] 妃 [ 0.3 0.375 0.5] 这样,我们就把一些词甚至一个字,用三个特征给表征出来了。然后,我们把皇帝叫做特征(1),宫里叫做特征(2),女叫做特征(3),于是乎,我们就得出了公主和王妃的隐含特征关系:
王妃=公主的特征(1) * 0.6 +公主的特征(2) * 3 +公主的特征(3) * 1
于是乎,我们把文字的one-hot编码,从稀疏态变成了密集态,并且让相互独立向量变成了有内在联系的关系向量。
所以,embedding层做了个什么呢?它把我们的稀疏矩阵,通过一些线性变换(在CNN中用全连接层进行转换,也称为查表操作),变成了一个密集矩阵,这个密集矩阵用了N(例子中N=3)个特征来表征所有的文字,在这个密集矩阵中,表象上代表着密集矩阵跟单个字的一一对应关系,实际上还蕴含了大量的字与字之间,词与词之间甚至句子与句子之间的内在关系(如:我们得出的王妃跟公主的关系)。他们之间的关系,用的是嵌入层学习来的参数进行表征。
从稀疏矩阵到密集矩阵的过程,叫做embedding,很多人也把它叫做查表,因为他们之间也是一个一一映射的关系。
更重要的是,这种关系在反向传播的过程中,是一直在更新的,因此能在多次epoch后,使得这个关系变成相对成熟,即:正确的表达整个语义以及各个语句之间的关系。这个成熟的关系,就是embedding层的所有权重参数。
Embedding是NPL领域最重要的发明之一,他把独立的向量一下子就关联起来了。这就相当于什么呢,相当于你是你爸的儿子,你爸是A的同事,B是A的儿子,似乎跟你是八竿子才打得着的关系。结果你一看B,是你的同桌。Embedding层就是用来发现这个秘密的武器。
torch.nn.Embedding是PyTorch中的一个嵌入层,它可以将离散的输入(如单词的索引)映射到连续的向量空间中。下面是一些使用
torch.nn.Embedding的例子:
1. 单词嵌入(Word Embedding)
在自然语言处理(NLP)任务中,我们通常将单词表示为一个整数索引,然后使用嵌入层将这些索引映射到一个连续的向量空间中。这样,语义上相似的单词会被映射到向量空间中的相近位置。
1 | import torch |
2. 位置嵌入(Positional Embedding)
在序列数据中,位置信息非常重要,因为序列中的元素顺序会影响其含义。位置嵌入层的作用就是给每个位置分配一个唯一的向量,这样模型就可以学习到位置信息。
1 | import torch |
3. 图像嵌入(Image Embedding)
在计算机视觉任务中,我们通常将图像表示为一个像素值的张量。然后,我们可以使用嵌入层将这些像素值映射到一个连续的向量空间中,以便进行进一步的处理或分析。
1 | import torch |
在这些例子中,我们使用
torch.nn.Embedding将离散的输入(如单词索引、位置索引或像素索引)映射到连续的向量空间中。这些向量可以捕捉到输入值的一些语义信息,从而更好地处理数据。
池化层
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合
简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像
池化层的作用
主要是两个作用:
- invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度)
- 保留主要的特征同时减少参数(降维,效果类似PCA)和计算量,防止过拟合,提高模型泛化能力
A: 特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
B. 特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用
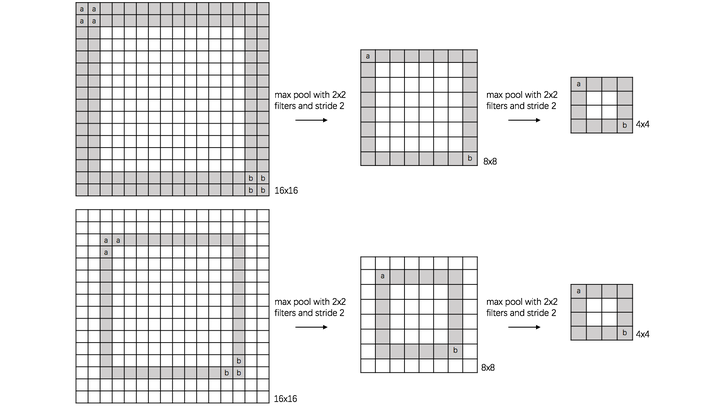
translation invariance: 这里举一个直观的例子(数字识别),假设有一个16x16的图片,里面有个数字1,我们需要识别出来,这个数字1可能写的偏左一点(图1),这个数字1可能偏右一点(图2),图1到图2相当于向右平移了一个单位,但是图1和图2经过max pooling之后它们都变成了相同的8x8特征矩阵,主要的特征我们捕获到了,同时又将问题的规模从16x16降到了8x8,而且具有平移不变性的特点。图中的a(或b)表示,在原始图片中的这些a(或b)位置,最终都会映射到相同的位置。
rotation invariance: 下图表示汉字“一”的识别,第一张相对于x轴有倾斜角,第二张是平行于x轴,两张图片相当于做了旋转,经过多次max pooling后具有相同的特征 ————————————————
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/weixin_38145317/article/details/89310404
池化层用的方法有Max pooling 和 average pooling
Max pooling:
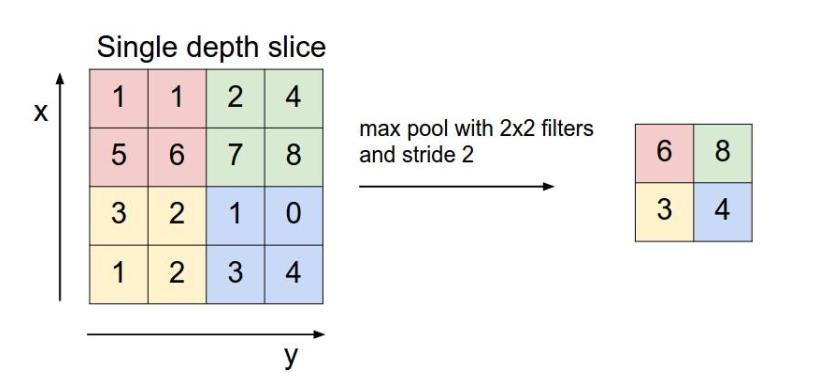
对于每个22的窗口选出最大的数作为输出矩阵的相应元素的值,比如输入矩阵第一个22窗口中最大的数是6,那么输出矩阵的第一个元素就是6,如此类推。
逻辑回归
1. 什么是逻辑回归
逻辑回归是用来做分类算法的,大家都熟悉线性回归,一般形式是Y=aX+b,y的取值范围是[-∞, +∞],有这么多取值,怎么进行分类呢?不用担心,伟大的数学家已经为我们找到了一个方法。
也就是把Y的结果带入一个非线性变换的Sigmoid函数中,即可得到[0,1]之间取值范围的数S,S可以把它看成是一个概率值,如果我们设置概率阈值为0.5,那么S大于0.5可以看成是正样本,小于0.5看成是负样本,就可以进行分类了。
2. 什么是Sigmoid函数
函数公式如下:
函数中t无论取什么值,其结果都在[0,-1]的区间内,回想一下,一个分类问题就有两种答案,一种是“是”,一种是“否”,那0对应着“否”,1对应着“是”,那又有人问了,你这不是[0,1]的区间吗,怎么会只有0和1呢?这个问题问得好,我们假设分类的阈值是0.5,那么超过0.5的归为1分类,低于0.5的归为0分类,阈值是可以自己设定的。
好了,接下来我们把aX+b带入t中就得到了我们的逻辑回归的一般模型方程:
结果P也可以理解为概率,换句话说概率大于0.5的属于1分类,概率小于0.5的属于0分类,这就达到了分类的目的。
3. 损失函数是什么
逻辑回归的损失函数是 log loss ,也就是 对数似然函数 ,函数公式如下:
公式中的 y=1 表示的是真实值为1时用第一个公式,真实 y=0 用第二个公式计算损失。为什么要加上log函数呢?可以试想一下,当真实样本为1是,但h=0概率,那么log0=∞,这就对模型最大的惩罚力度;当h=1时,那么log1=0,相当于没有惩罚,也就是没有损失,达到最优结果。所以数学家就想出了用log函数来表示损失函数。
最后按照梯度下降法一样,求解极小值点,得到想要的模型效果。
4.可以进行多分类吗?
可以的,其实我们可以从二分类问题过度到多分类问题(one vs rest),思路步骤如下:
1.将类型class1看作正样本,其他类型全部看作负样本,然后我们就可以得到样本标记类型为该类型的概率p1。
2.然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2。
3.以此循环,我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi,最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
总之还是以二分类来依次划分,并求出最大概率结果.
5.逻辑回归有什么优点
- LR能以概率的形式输出结果,而非只是0,1判定。
- LR的可解释性强,可控度高(你要给老板讲的嘛…)。
- 训练快,feature engineering之后效果赞。
- 因为结果是概率,可以做ranking model。
6. 逻辑回归有哪些应用
- CTR预估/推荐系统的learning to rank/各种分类场景。
- 某搜索引擎厂的广告CTR预估基线版是LR。
- 某电商搜索排序/广告CTR预估基线版是LR。
- 某电商的购物搭配推荐用了大量LR。
- 某现在一天广告赚1000w+的新闻app排序基线是LR。
7. 逻辑回归常用的优化方法有哪些
7.1 一阶方法
梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
7.2 二阶方法:牛顿法、拟牛顿法:
这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。
在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
拟牛顿法: 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、 L-BFGS(可以减少BFGS所需的存储空间)。
8. 逻辑斯特回归为什么要对特征进行离散化。
- 非线性!非线性!非线性!逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合; 离散特征的增加和减少都很容易,易于模型的快速迭代;
- 速度快!速度快!速度快!稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
- 鲁棒性!鲁棒性!鲁棒性!离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
- 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 稳定性:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
- 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
9. 逻辑回归的目标函数中增大L1正则化会是什么结果。
所有的参数w都会变成0。
10. 代码实现
.
把数据切分成训练集和测试集
1 | from sklearn import model_selection |
使用logistic regression/决策树/SVM/KNN...等sklearn分类算法进行分类,尝试查sklearn API了解模型参数含义,调整不同的参数。
1 | from sklearn.linear_model import LogisticRegression |
1 | 0.9323730412572769 |
.
在测试集上进行预测,计算准确度
1 | from sklearn.metrics import accuracy_score |
1 | 训练集准确率: 0.9323730412572769 |
.
查看sklearn的官方说明,了解分类问题的评估标准,并对此例进行评估。
例如,如果这是一个将水果分为苹果、香蕉、橙子的多分类问题。召回率衡量的是对于每个类别,模型正确预测为该类别的样本数量占实际该类别样本数量的比例。通过计算训练集和测试集的召回率,可以评估模型在不同数据集上对各类别样本的预测能力,从而判断模型是否过拟合或欠拟合,以及模型在新数据上的泛化能力。
1 | ##召回率 |
1 | 训练集召回率: 0.4999938302834368 |
.
银行通常会有更严格的要求,因为fraud带来的后果通常比较严重,一般我们会调整模型的标准。 比如在logistic regression当中,一般我们的概率判定边界为0.5,但是我们可以把阈值设定低一些,来提高模型的“敏感度”,试试看把阈值设定为0.3,再看看这时的评估指标(主要是准确率和召回率)。
tips:sklearn的很多分类模型,predict_prob可以拿到预估的概率,可以根据它和设定的阈值大小去判断最终结果(分类类别)
1 | import numpy as np |
1 | 0.9333179935572941 |
各种图示
箱线图/箱型图/箱形图

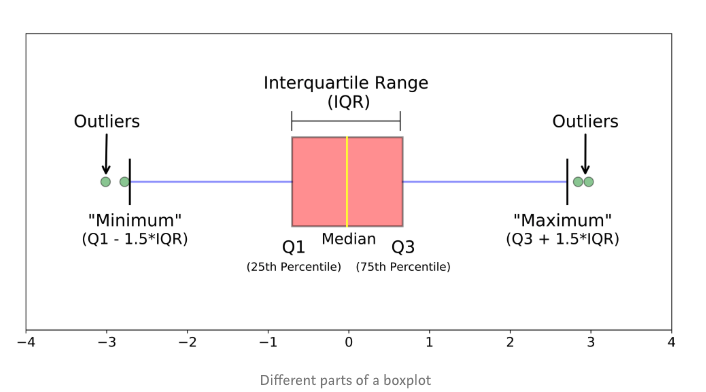
如上图箱线图,箱线图是一个能够通过5个数字来描述数据的分布的标准方式,这5个数字包括:最小值,第一分位,中位数,第三分位数,最大值,箱线图能够明确的展示离群点的信息,同时能够让我们了解数据是否对称,数据如何分组、数据的峰度;
1. 什么是箱线图?
对于某些分布/数据集,您会发现除了集中趋势(中位数,均值和众数)的度量之外,您还需要更多信息。
您需要有关数据变异性或分散性的信息。 箱形图是一张图表,它为您很好地指示数据中的值如何分布,尽管与直方图或密度图相比,箱线图似乎是原始的,但它们具有占用较少空间的优势,这在比较许多组或数据集之间的分布时非常有用。
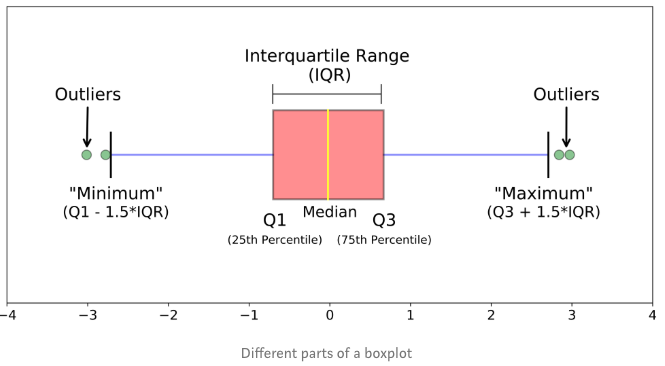
箱线图是一种基于五位数摘要(“最小”,第一四分位数(Q1),中位数,第三四分位数(Q3)和“最大”)显示数据分布的标准化方法。
- 中位数(Q2 / 50th百分位数):数据集的中间值;
- 第一个四分位数(Q1 / 25百分位数):最小数(不是“最小值”)和数据集的中位数之间的中间数;
- 第三四分位数(Q3 / 75th Percentile):数据集的中位数和最大值之间的中间值(不是“最大值”);
- 四分位间距(IQR):第25至第75个百分点的距离;
- 晶须(蓝色显示)
- 离群值(显示为绿色圆圈)
- “最大”:Q3 + 1.5 * IQR
- “最低”:Q1 -1.5 * IQR
离群值,“最小”或“最大”的内容可能尚不清楚。下一节将尽力为您解决问题;
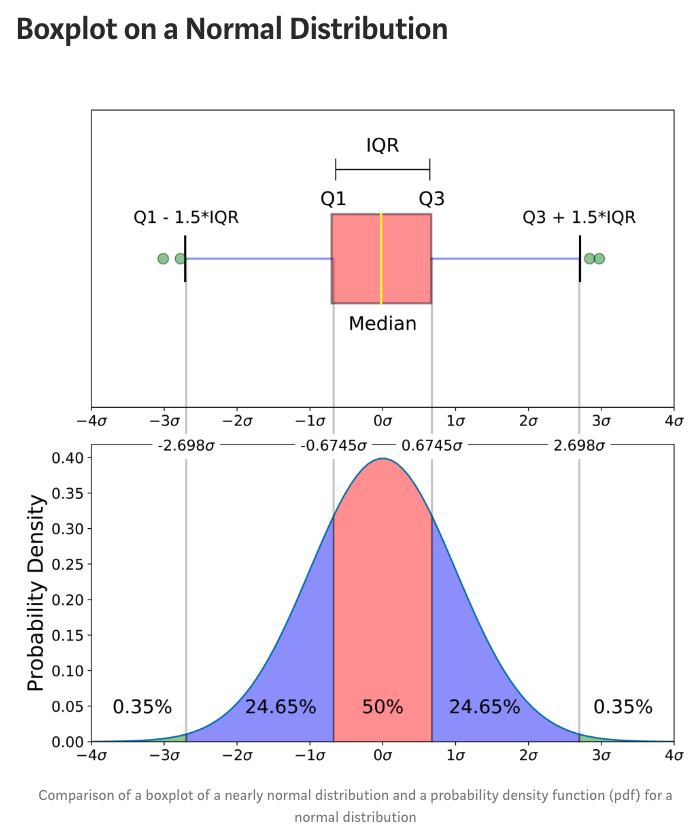
上图是近似正态分布的箱线图与正态分布的概率密度函数(pdf)的比较,我向您显示此图像的原因是,查看统计分布比查看箱形图更为普遍。换句话说,它可以帮助您理解箱线图;
本节将涵盖许多内容,包括:
- 对于正态分布而言,0.7%的数据异常值;
- 什么是“最小”和“最大”
概率密度函数
帖子的这一部分与68–95–99.7规则文章非常相似,但适用于箱线图,为了了解百分比的来源,重要的是要了解概率密度函数(PDF),PDF用于指定随机变量落入特定值范围内的概率,而不是任何一个具体值,该概率由该变量在该范围内的PDF的积分得出,也就是说,它是由密度函数下方但水平轴上方以及范围的最小值和最大值之间的面积给出的,这个定义可能没有多大意义,因此让我们通过绘制正态分布的概率密度函数来理解它,下式是正态分布的概率密度函数:
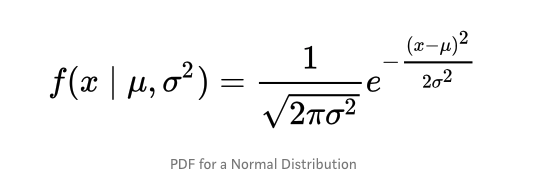
让我们简化一下,假设我们的平均值(μ)为0,标准偏差(σ)为1:
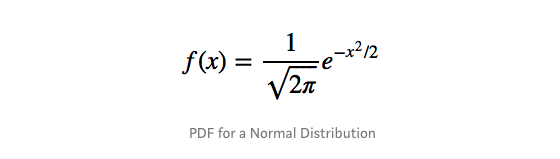
可以使用任何图形进行绘制,但是我选择使用Python进行图形绘制
1 | # Import all libraries for this portion of the blog post |
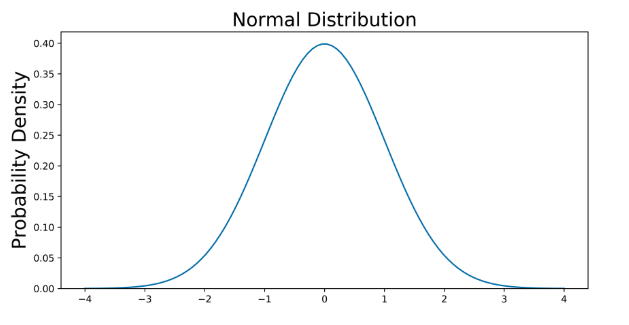
上图没有显示事件的概率,而是事件的概率密度,为了获得事件在给定范围内的概率,我们需要进行积分,假设我们感兴趣的是寻找随机数据点落在四分位数范围内的概率。平均值的.6745标准偏差,我们需要将-0.6745集成到0.6745。这可以用SciPy完成.
1 | # Make PDF for the normal distribution a function |
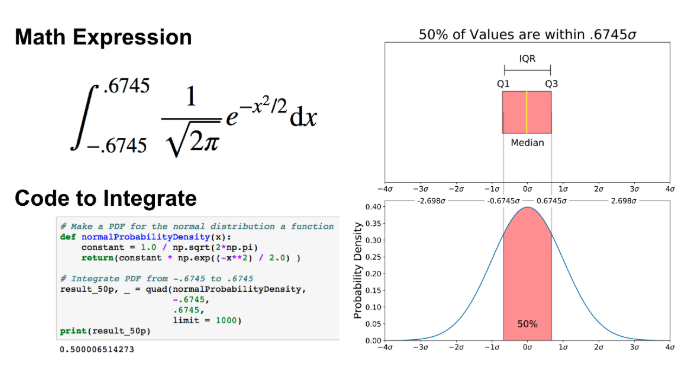
可以对“最小”和“最大”执行相同的操作
1 | # Make a PDF for the normal distribution a function |
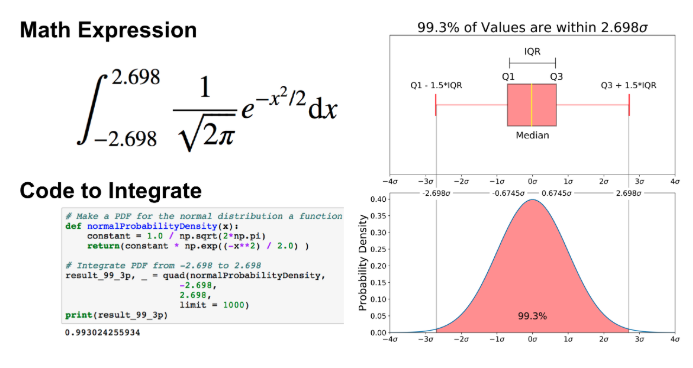
如前所述,离群值是数据的剩余0.7%. 请务必注意,对于任何PDF,曲线下的面积必须为1(从函数范围内绘制任何数字的概率始终为1)
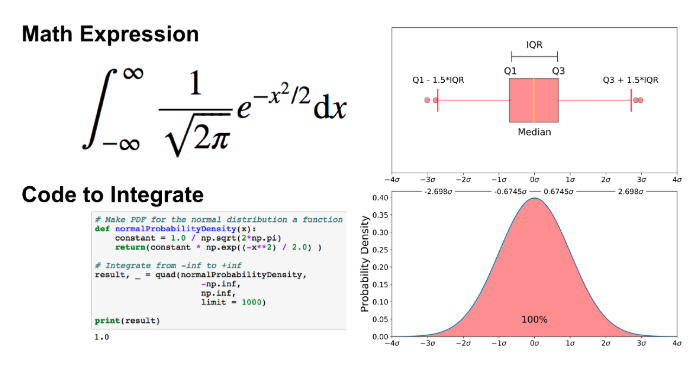
本部分主要基于我的Python for Data Visualization课程的免费预览视频。在上一节中,我们介绍了正态分布的箱线图,但是由于您显然并不总是具有基本的正态分布,因此让我们研究一下如何在真实数据集上利用箱形图。为此,我们将利用乳腺癌威斯康星州(诊断)数据集.
读取数据
1 | import pandas as pd |
箱线图
下面使用箱线图来分析分类特征(恶性或良性肿瘤)和连续特征(area_mean)之间的关系。
seaborn
1 | sns.boxplot(x='diagnosis', y='area_mean', data=df) |
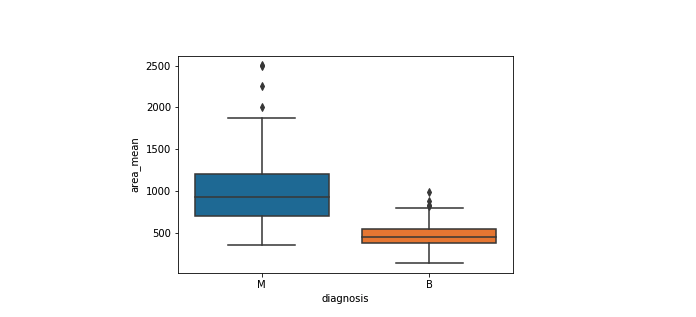
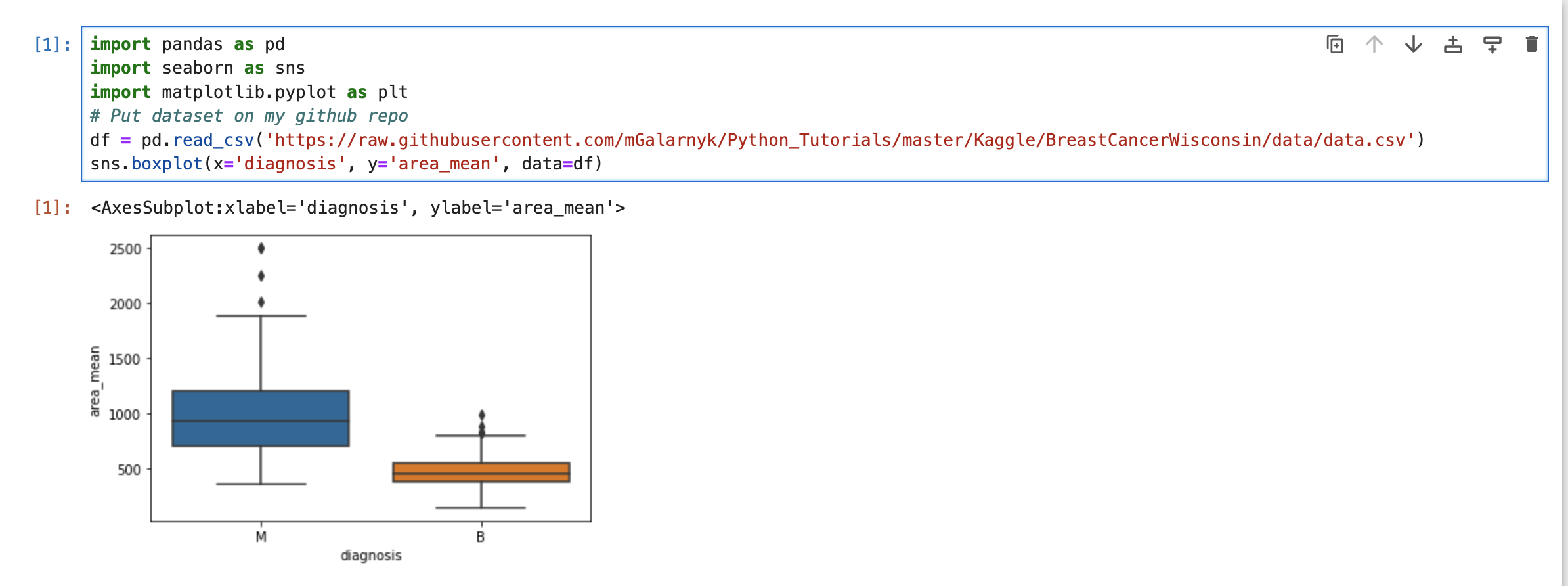
使用该图,我们可以比较Area_mean的范围和分布,以进行恶性和良性诊断。我们观察到,恶性肿瘤的Area_mean以及较大的异常值存在较大的变异性。 另外,由于箱线图中的凹口不重叠,因此可以得出结论,在95%的置信度下,真实中位数确实有所不同.
关于箱线图,还有一些其他注意事项:
- 请记住,如果您想知道箱线图不同部分的数值是什么,可以随时从箱线图中提取数据。
- Matplotlib不会首先估计正态分布,而是根据估计的分布参数计算四分位数,中位数和四分位数直接从数据中计算得出。换句话说,您的箱形图看起来可能会有所不同,具体取决于数据的分布和样本的大小,例如,不对称且具有或多或少的异常值
1.3箱型图的缺点 1.箱型图虽然能显示出数据的分布偏态,但是不能提供关于数据分布偏态和尾重程度的精确度量;
2.对于批量较大的数据批,箱线图反映的形状信息更加模糊;
3.用中位数代表总体平均水平有一定的局限性。
所以,应用箱线图最好结合其它描述统计工具如均值、标准差、偏度、分布函数等来描述数据批的分布形状。
核密度图
why-为什么需要做核密度图?
- 核密度图(kernel density plot)是一种很重要的数据可视化图形
- 它可以直观展示出数据分布的形状,以及可以帮助识别异常值
- 相较于柱状图(histogram),它所展示的数据分布并不受bins影响
- 它是根据有限的样本数据对总体数据概率密度的估计
总而言之,它可以展示出数据的整体分布,且比柱状图更具有优势
what-核密度图是什么?
核密度图本质上是根据有限的数据样本,运用核密度函数,对整体数据的密度进行估计;即已知有限的数据样本和一个核函数,输出整体数据的概率密度,并通过图形展示出结果
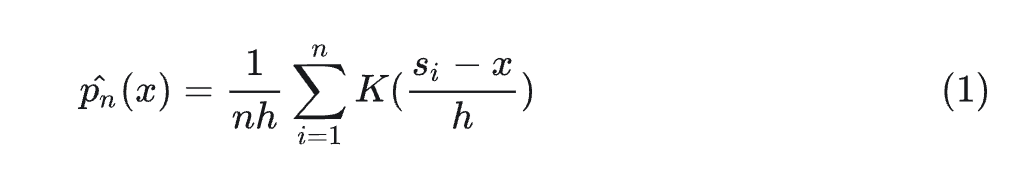
其中
x是属于整体数据中的任一变量
n是样本数据中数据点的个数
h是平滑带宽,控制平滑量,h值越大,数据越平滑;且h>0
K是核密度函数
si是样本数据中的一个数据点
核密度函数必须满足以下三个属性:
- 核密度函数必须是对称的
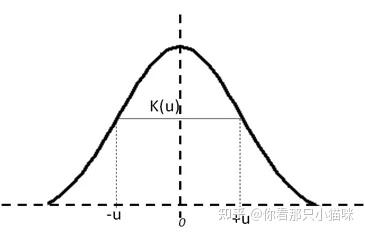
- 核密度函数曲线下的面积必须为1

- 核函数值要大于等于0

目前常用的核函数为
高斯(Gaussian)分布概率密度函数

- 均匀(Uniform)分布概率密度函数
- Epanechnikov密度函数
- ...
How-怎么做核密度图?
以高斯核为例,我们将公式4带入到公式1中,可以得到高斯核密度函数为
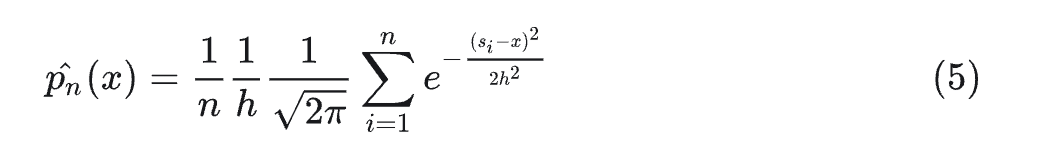
也可以写成

其中
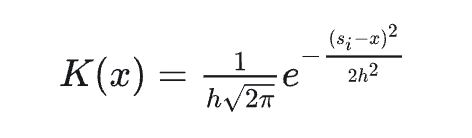
我们从公式6就可以看出,我们是对多个概率密度求了平均
接下来我们以一组数据为例,展示其在高斯核密度函数计算过程
我们在计算之前已知的数据如下:
- 一组样本数据S = {65,75,67,79,81,91}, 即s1= 65, s2=75.....
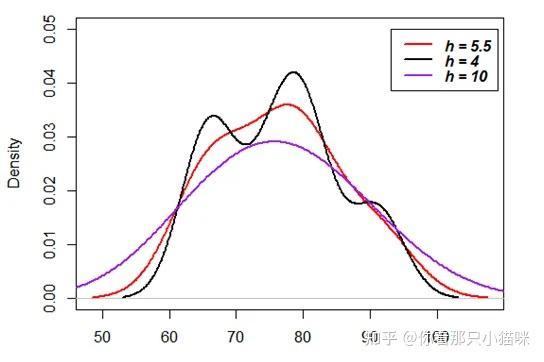
- 预先设置好h值,比如h = 5.5
- 一组线性间隔的数据点且该数据点包含S内的数据,记为X = 50,51,52...99
对于一个样本点si, 我们计算公式6中的K(x),x在X中取值
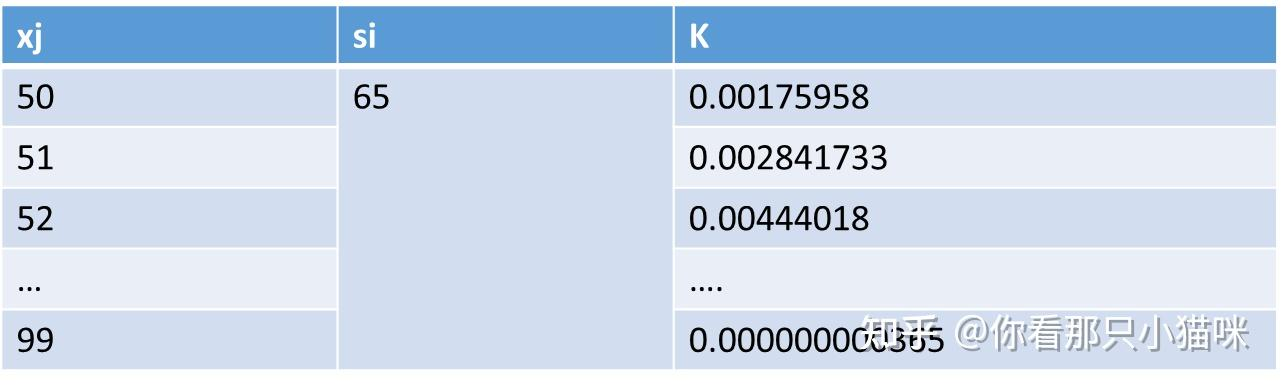
按照上述方法,我们依次计算S内的其他样本点,最终,每一个样本点都有一个这样的表格,汇总起来就是下表,假设里面是有数值的
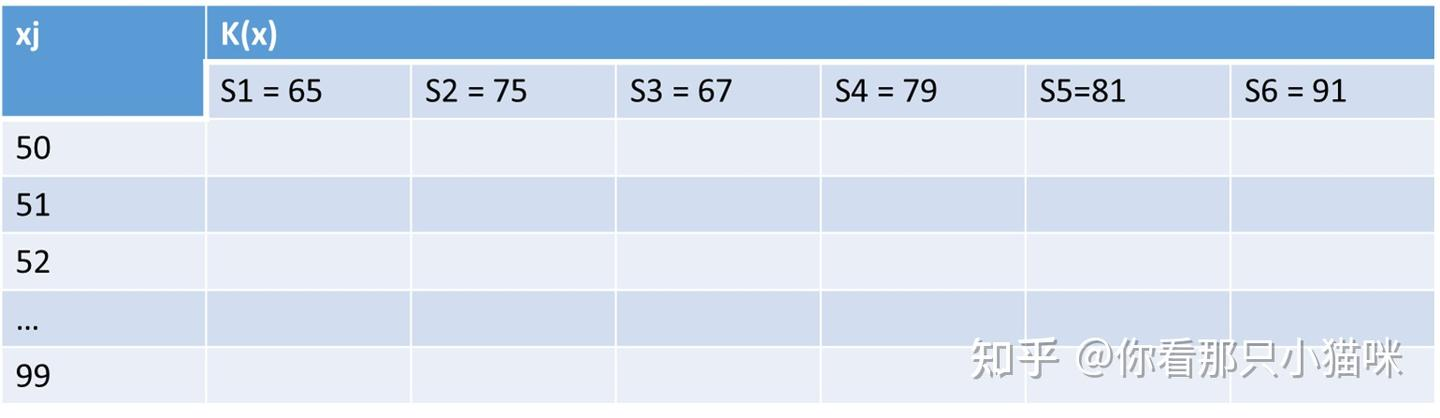
如果我们画出图形就是下图
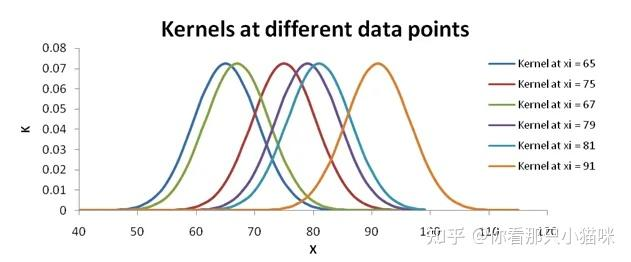
对于某一点xj来说,其概率密度为上述6个样本点在xj处所计算出的概率密度值的平均
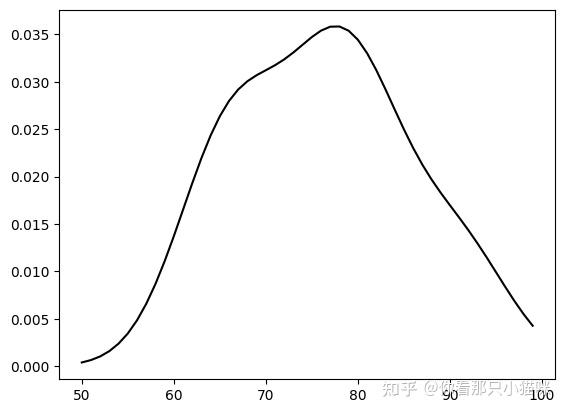
下面是代码实现过程
1 |
|
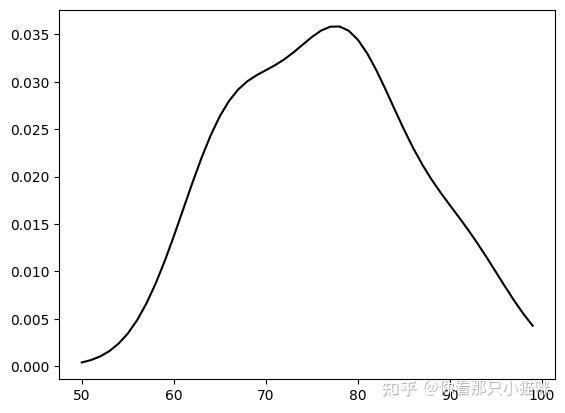
1 | ## 实现版本2, 根据seaborn内的函数kdeplot |
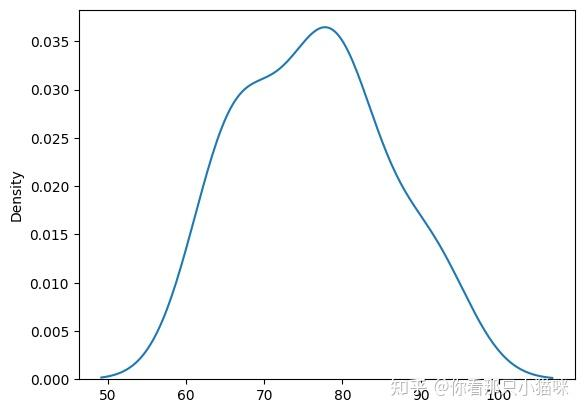
注意: bw_method 是设置h值,这里当设置为5.5时,与版本1的结果不同,这是因为sns.kdeplot还进行了一些矫正
需要注意
- h是很重要的参数,h值越大,平滑程度越高;具体见下图
该密度估计方法是一种有偏估计
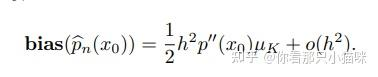
小提琴图
般来说,小提琴图是一种绘制连续型数据的方法,可以认为是箱形图与核密度图的结合体。当然了,在小提琴图中,我们可以获取与箱形图中相同的信息。
- 中位数(小提琴图上的一个白点)
- 四分位数范围(小提琴中心的黑色条)。
- 较低/较高的相邻值(黑色条形图)--分别定义为第一四分位数-1.5 IQR和第三四分位数+1.5 IQR。这些值可用于简单的离群值检测技术,即位于这些 "栅栏"之外的值可被视为离群值。
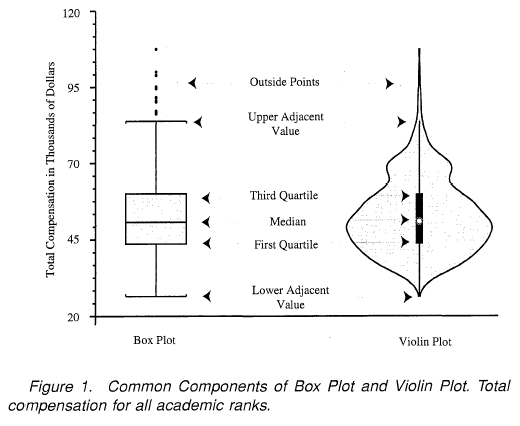
与箱形图相比,小提琴图毫无疑问的优势在于:除了显示上述的统计数据外,它还显示了数据的整体分布。这个差异点很有意义,特别是在处理多模态数据时,即有多峰值的分布。
用Python实现 在这篇文章中,我们使用了以下库:
- seaborn
- numpy
- pandas
- matplotlib
我们首先定义了我们随机观测值的数量,以及为结果的设置的随机种子。
1 | N = 10 ** 4 |
然后,我们定义一个函数来绘制以下内容。
- 带有内核密度估计的直方图(KDE)。
- 波谱图
- 一个小提琴图 我们将使用这个函数来描述随机创建的样本特性。
1 | def plot_comparison(x, title): |
1. 标准正态分布
我们从最基本的分布开始--标准正态分布。我们随机抽取10000个数字,并绘制结果。
正态分布参考:如何通俗的理解正态分布 - 知乎 (zhihu.com)
1 | sample_gaussian = np.random.normal(size=N) |
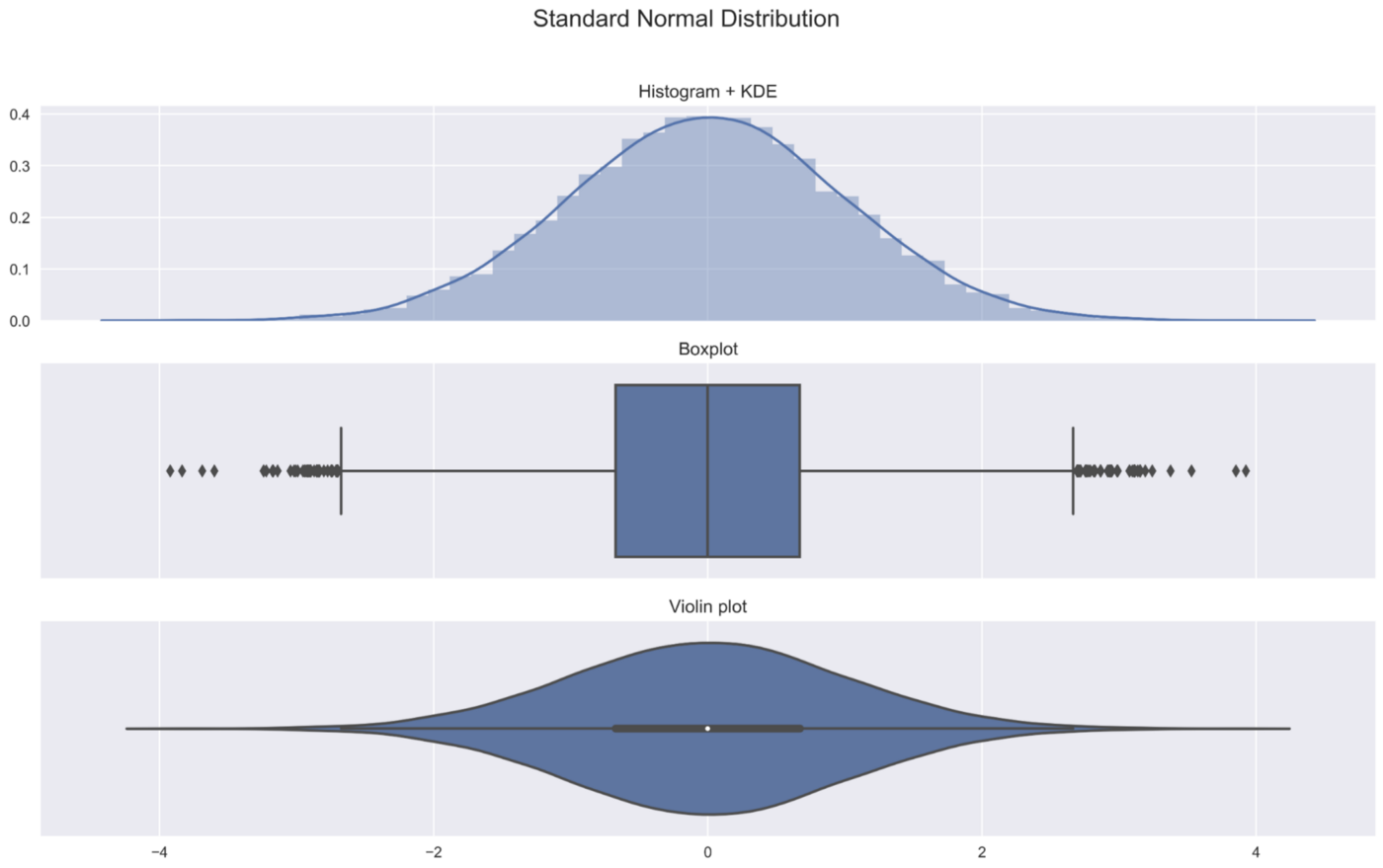
可以得到一些直观感受:
- 在直方图中,我们看到分布的对称形状
- 我们可以在箱形图和小提琴图中看到前面提到的指标(中位数、IQR)。
- 用于创建小提琴图的核密度图与添加在直方图上的核密度图是一样的。小提琴图中较宽的部分代表观测值取值的概率较高,较窄的部分则对应于较低的概率。 我相信,将这三张图放在一起展示,可以清晰的看到小提琴图什么样子以及它包含什么样的直觉信息。
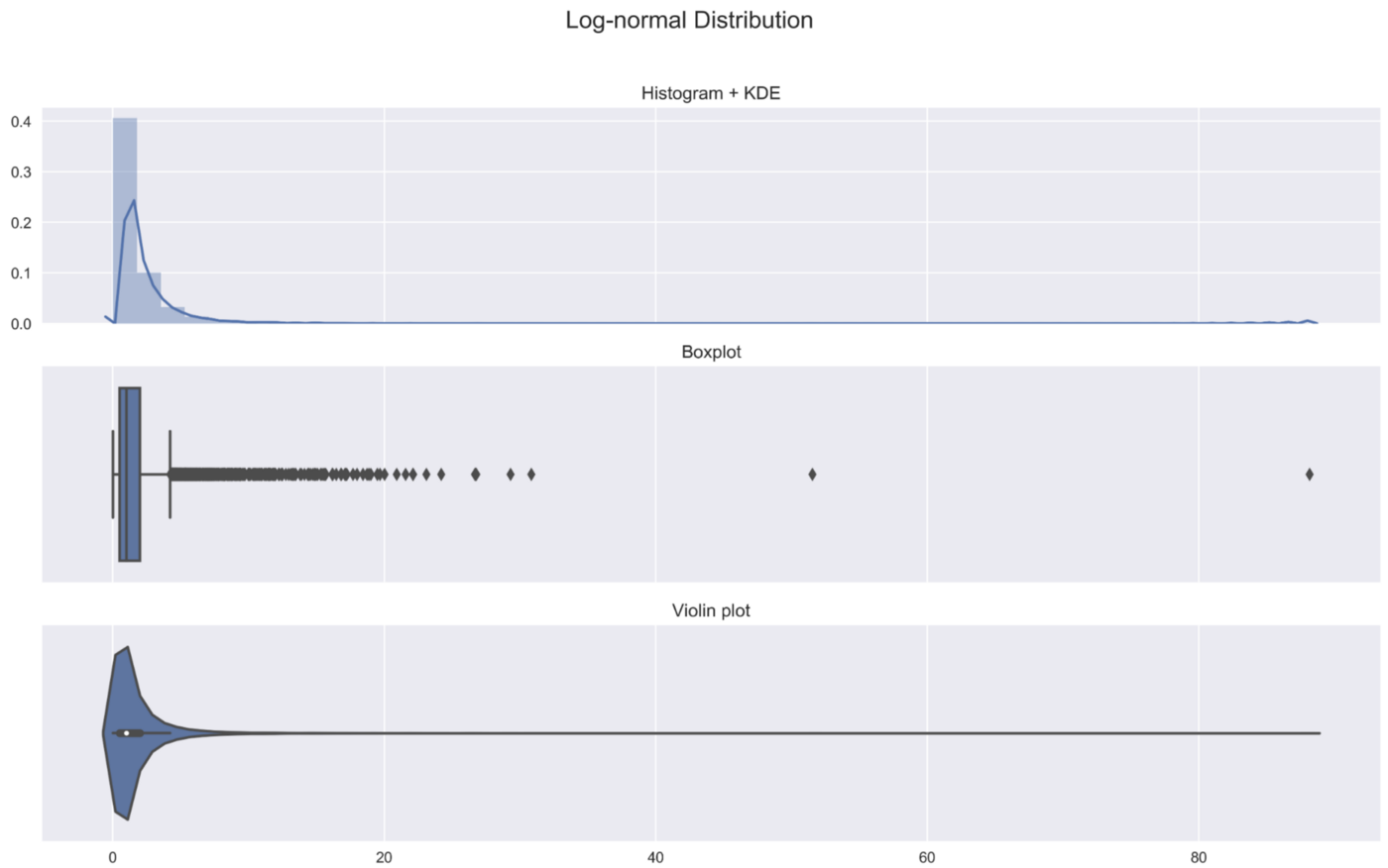
2. 对数正态分布
在第二个例子中,我们考虑对数正态分布,它肯定比正态分布更加偏斜。
1 | sample_lognormal = np.random.lognormal(size=N) |
3. 高斯的混合体--双峰型
在前面两个例子中,我们已经看到小提琴图比箱形图包含更多的信息。当我们考虑一个多模态分布时,这一点就更加明显了。在这个例子中,我们创建了一个双模分布,作为两个高斯分布的混合体。
高斯混合模型可以参考:如何通俗的理解高斯混合模型(Gaussian Mixture Models) - 知乎 (zhihu.com)
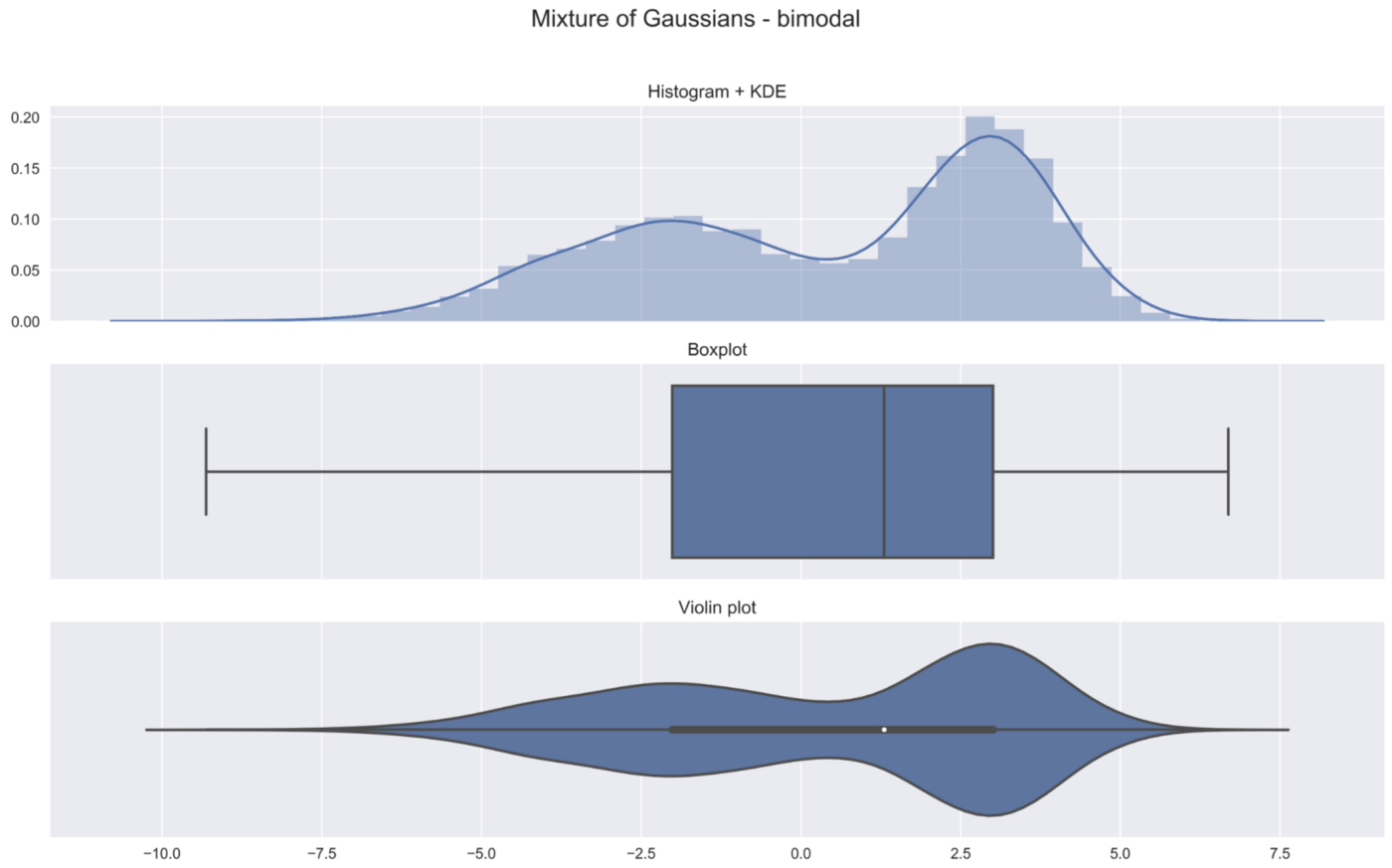
如果不看直方图/密度图,就不可能发现我们数据中的两个峰值。
4. 高级用法
小提琴图经常被用来比较一个给定变量在某些类别中的分布。我们在下面介绍一些可能性。要做到这一点,我们从seaborn加载tips数据集。
1 | tips = sns.load_dataset("tips") |
在第一个例子中,我们可以看到每个性别的分布。此外,我们改变小提琴图的结构,只显示四分位数。其他一些包括显示所有观测值的点或在小提琴图内画一个小方框图。
1 | ax = sns.violinplot(x="sex", y="tip", inner='quartile', data=tips) |
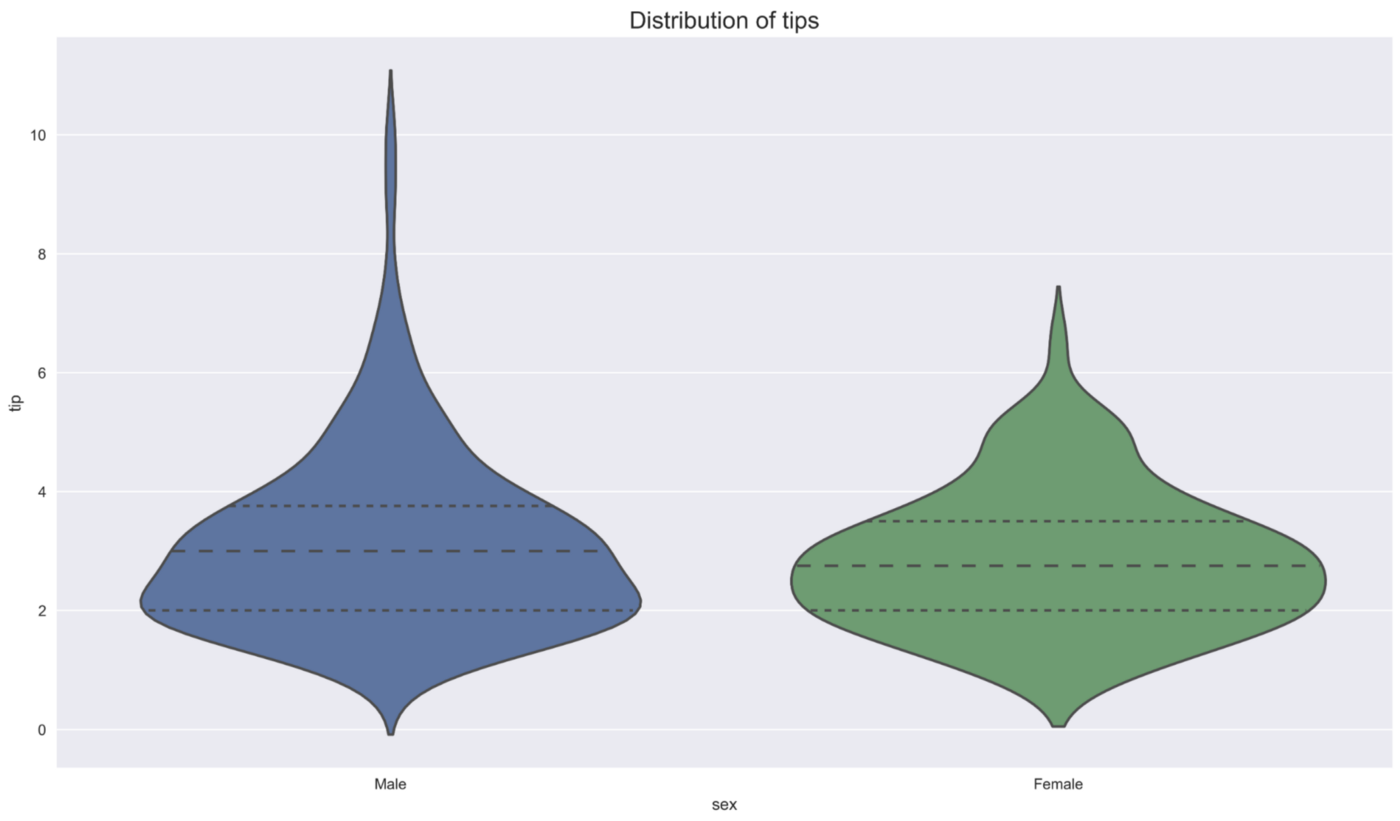
我们看到,两种性别的tips的总体形状和分布是相似的(四分位数非常接近),但在男性中有更多的离群值。
在第二个例子中,我们查看每天总账单金额的分布。此外,我们按性别划分。我们就立马能够看到,性别之间分布形状的最大差异发生在星期五。
1 | ax = sns.violinplot(x="day", y="total_bill", hue="sex", data=tips) |
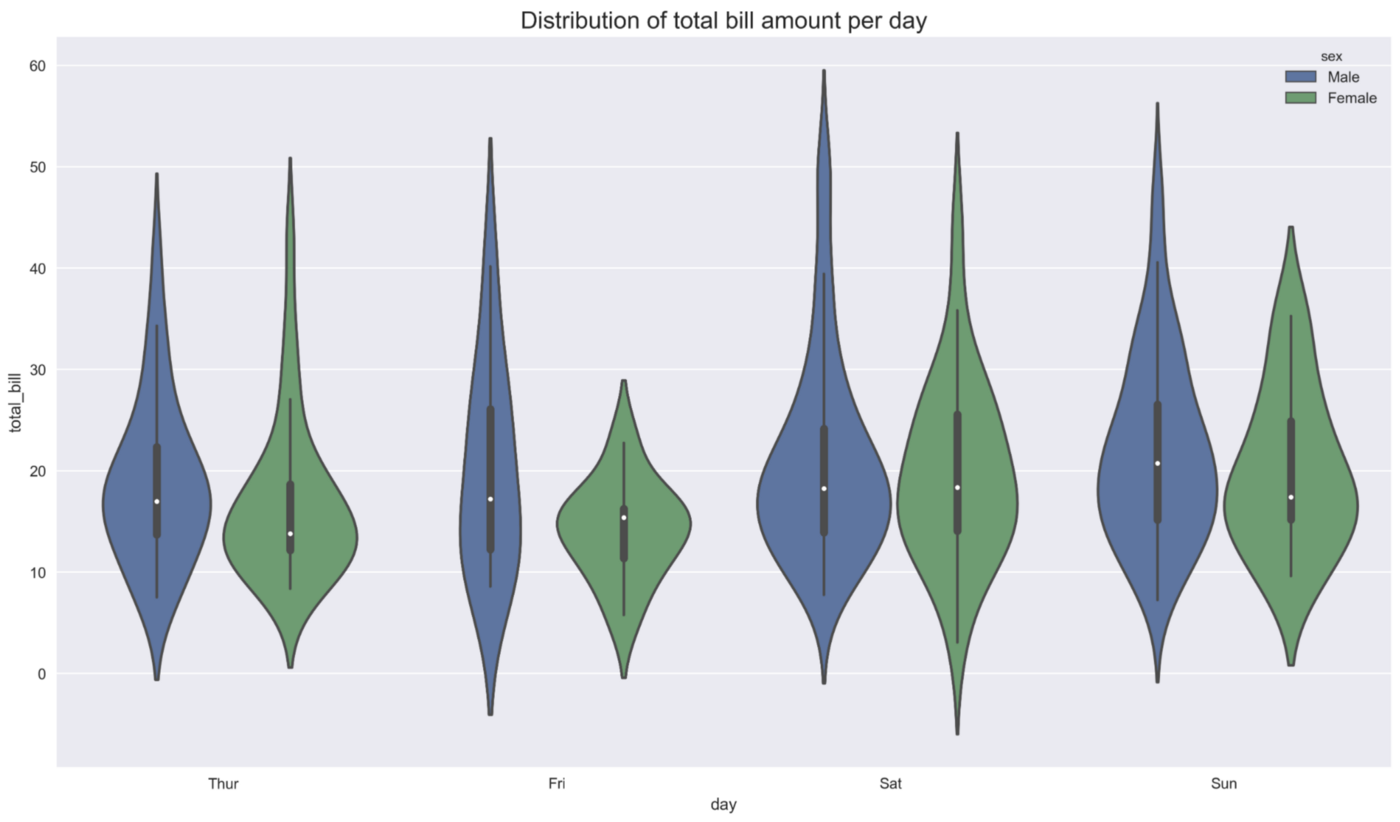
在最后一个例子中,我们调查的内容与前面的情况相同,但是,我们设置split=True。设置之后,我们最终得到的不是8把小提琴,而是4把--小提琴的每一侧都对应着不同的性别。
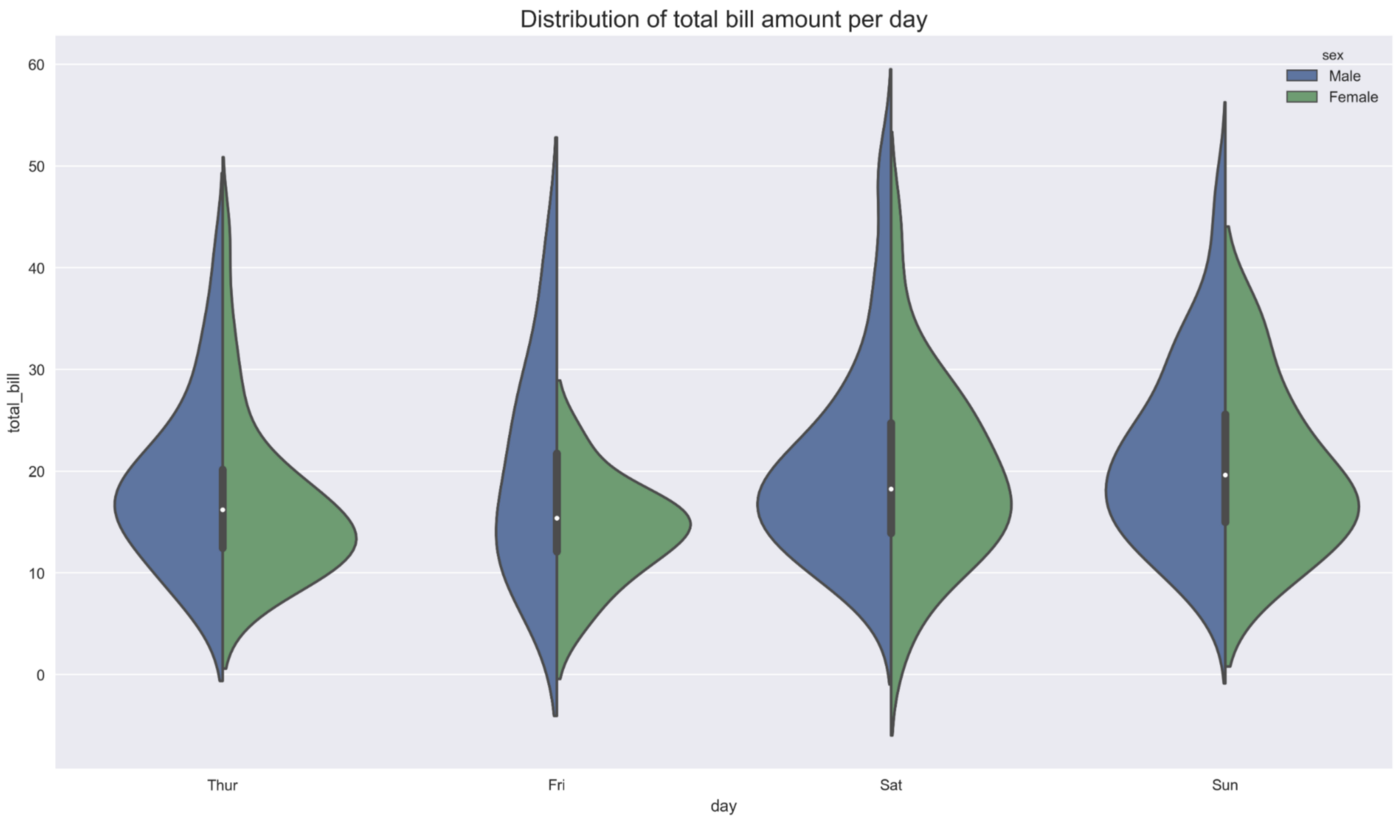
1 | ax = sns.violinplot(x="day", y="total_bill", hue="sex", split=True, data=tips) |
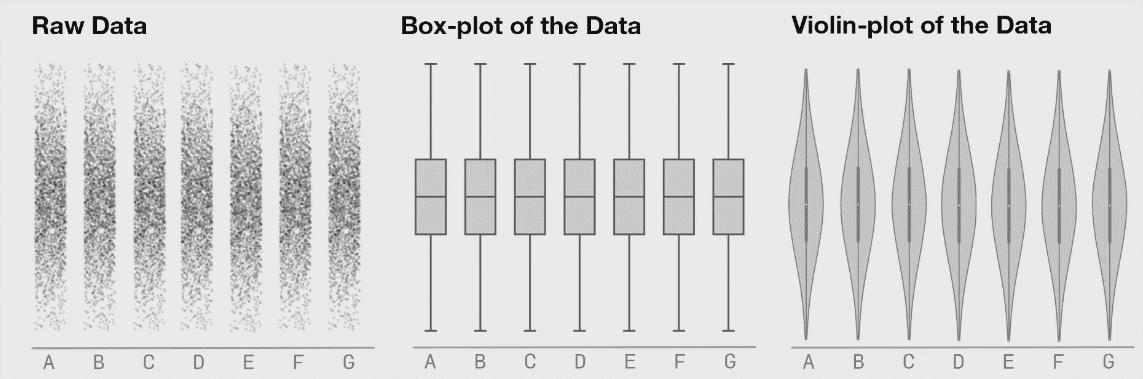
结论 在这篇文章中,我展示了什么是小提琴图,如何解释它们,以及它们比箱形图有什么优势。最后值得一提的是,如果数据的四分位数保持不变,箱形图就不会改变。那么,我们可以对数据进行修改,使四分位数不发生变化,但分布的形状会发生很大的变化。下面的GIF图说明了这一点。
t-SNE(t-distributed Stochastic Neighbor Embedding)
数学原理设计 t-分布和联合概率分布见 https://www.cnblogs.com/BlairGrowing/p/15400721.html
t-SNE(t-distributed Stochastic Neighbor Embedding)是一种用于降维和数据可视化的机器学习算法。
一、主要原理
t-SNE 的目标是将高维数据映射到低维空间(通常是二维或三维),同时尽可能保持数据点之间的相似性。
它通过将高维空间中的欧氏距离转换为概率分布,然后在低维空间中也构建一个概率分布,并最小化这两个概率分布之间的差异来实现。
具体来说,t-SNE 首先计算高维空间中数据点之间的相似性,通常使用高斯分布来计算两个点之间的相似度。然后,在低维空间中使用 t 分布来计算数据点之间的相似性。通过优化一个损失函数,使得低维空间中的相似性尽可能接近高维空间中的相似性。
二、应用场景
- 数据可视化:t-SNE 能够将高维数据可视化在二维或三维空间中,帮助人们直观地理解数据的分布和结构。例如,在图像分类任务中,可以将高维的图像特征映射到二维平面上,观察不同类别的图像在低维空间中的分布情况。
- 特征提取:t-SNE 可以作为一种特征提取方法,将高维数据映射到低维空间后,提取低维空间中的特征用于后续的分析和建模。
- 异常检测:通过观察数据在低维空间中的分布,可以发现异常点或离群点,这些点可能代表了数据中的异常情况或错误。
三、优势与局限性
优势:
- 能够有效地捕捉高维数据中的局部和全局结构,对于复杂的数据分布具有较好的可视化效果。
- 可以处理大规模数据集,通过随机采样和近似计算方法,减少计算时间和内存消耗。
局限性:
- 计算复杂度较高,尤其是对于大规模数据集,可能需要较长的计算时间。
- 结果具有一定的随机性,每次运行可能会得到不同的可视化结果。
- 在低维空间中的距离并不完全等同于高维空间中的距离,因此不能直接根据低维空间中的距离进行精确的度量和分析。
Inception思想
1. Inception-v1
1.1 为什么提出Inception
一般来说,提升网络性能最保险的方法就是增加网络的深度和宽度,但这样做同时也会伴随着副作用:
1、当越深越宽的网络往往会有着巨大的参数量,当数据量很少的时候,训练出来的网络容易过拟合
2、需要更多的计算资源
3、网络越深,梯度容易消失,优化困难(这时还没有提出BN时,网络的优化极其困难)
基于此,我们的目标就是,提高网络计算资源的利用率,在计算量不变的情况下,提高网络的宽度和深度。作者认为,解决这种困难的方法就是,把全连接改成稀疏连接,卷积层也是稀疏连接,但是不对称的稀疏数据数值计算效率低下,因为硬件全是针对密集矩阵优化的,所以,我们要找到卷积网络可以近似的最优局部稀疏结构,并且该结构下可以用现有的密度矩阵计算硬件实现,产生的结果就是Inception。
1.2 网络结构
Inception Module基本组成结构有四个成分。1x1卷积核,3x3卷积核,5x5卷积核,3x3最大池化。最后对四个成分运算结果进行通道上组合。
Inception结构如下图:
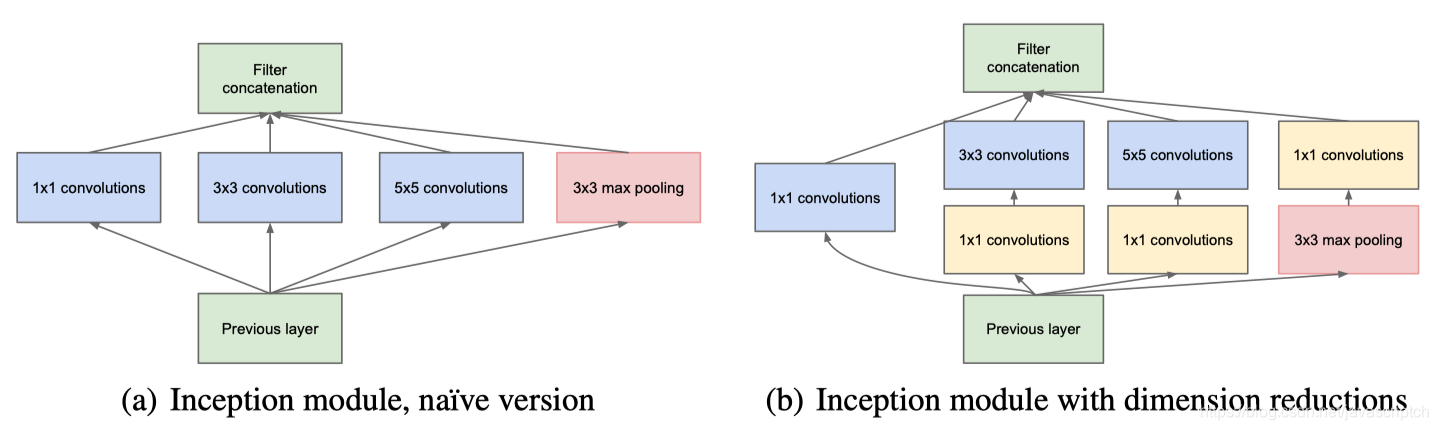
1.3 作用
Inception的核心思想:通过多个卷积核提取图像不同尺度的信息,最后进行融合,可以得到图像更好的表征
具体来说,假设我们要提取狗的脸部特征,不同图片中狗脸占比显然是不一样的,那么我们就需要使用不同大小的卷积核提取不同的信息。信息分布比较全局性的图像采用大卷积核,信息分布比较局部性的图像采用小卷积核。
作者提出的Inception的优点:
1、显著增加了每一步的单元数目,计算复杂度不会不受限制,尺度较大的特征在卷积之前先降维
2、视觉信息在不同尺度上进行处理融合,这样下一步可以从不同尺度提取特征
1.4 GoogLeNet
GoogLeNet是由Inception Module组成的,它的结构图:
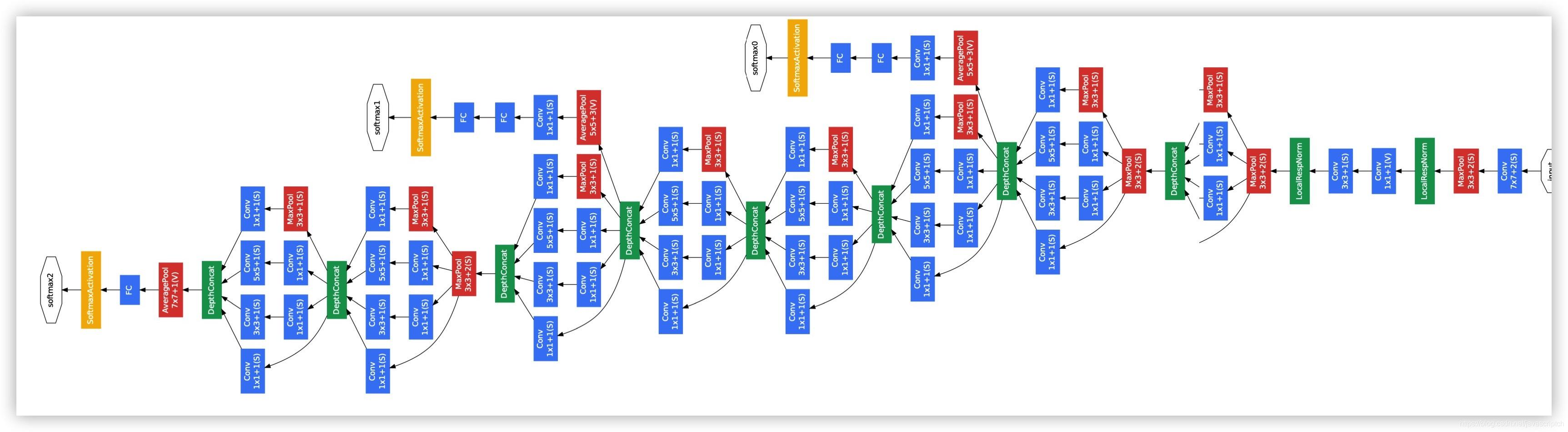
它的特点:
1、采用模块化结构,方便增加和修改。整个网络结构其实就是叠加Inception Module
2、使用Dropout层,防止过拟合
3、使用Averagepool来代替全连接层的思想。实际在最后一层还是添加了一个全连接层,是为了大家做finetune。
4、另外增加了两个辅助的softmax分支,作用有两点,一是为了避免梯度消失,用于向前传导梯度。反向传播时如果有一层求导为0,链式求导结果则为0。二是将中间某一层输出用作分类,起到模型融合作用。最后的loss=loss_2 + 0.3 * loss_1 + 0.3 * loss_0。实际测试时,这两个辅助softmax分支会被去掉。
Inception-v2
2.1 创新点 谷歌团队在2015年提出了Inception-v2,首次提出了批量归一化(Batch Normalization)方法,同时也改进了网络结构。具体的创新点:
2.1.1 Batch Normalization 在神经网络的每层计算中,参数变化导致数据分布不一致,会产生数据的协方差偏移问题,通过对第i层的数据进行BN操作,也就是对数据进行归一化。可以将数据控制在一定的范围内,在输入到第i+1层。可以提高网络的收敛能力,减少dropout的使用。
2.1.2 拆分卷积核 问题:
减少特征的表征性瓶颈。直观上来说,当卷积不会大幅度改变输入维度时,神经网络可能会执行地更好。过多地减少维度可能会造成信息的损失,这也称为「表征性瓶颈」。
使用更优秀的因子分解方法,卷积才能在计算复杂度上更加高效。
解决方法:
使用小的感受野代替大的感受野,v1版本中使用了5x5的卷积核,v2版本使用两个3x3的卷积核可以替代它。这样保证了感受野的范围还减少了参数量。并且增加了网络的深度,使表达能力更强。
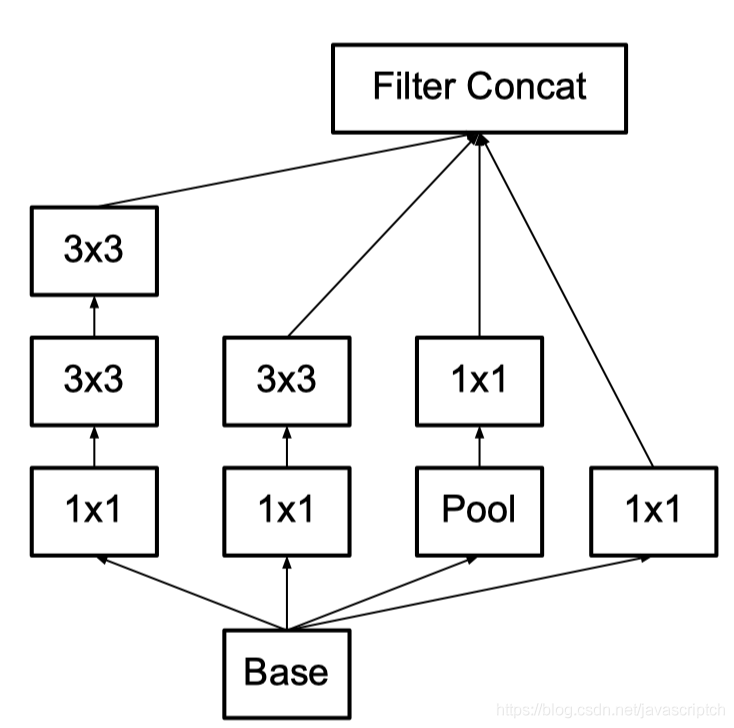
2.2 作用
1、批量归一化解决了协方差偏移的问题。让数据可控。即使使用大的学习率,网络也不会发生梯度消失或梯度爆炸的问题。减少了梯度对参数大小或初始值的依赖。还可以使用非线性饱和激活函数,因为可以避免陷入饱和状态。
2、卷积核的替换则可以保证感受野的同时,增加网络的表达能力。
Inception-v3
3.1 创新点 Inception V3对 Inception V2 主要进行了两个方面的改进。
首先,Inception V3 对 Inception Module 的结构进行了优化,现在 Inception Module有了更多的种类(有 35 × 35 、 1 7× 17 和 8× 8 三种不同结构),并且 Inception V3 还在 Inception Module 的分支中使用了分支(主要体现在 8x8 的结构中),如下图所示。
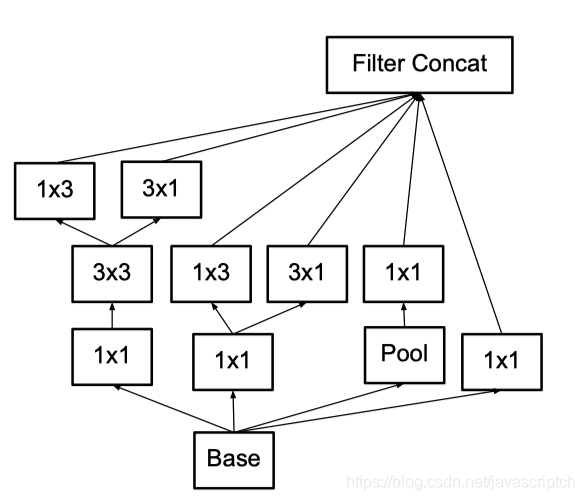
其次,在 Inception V3 中还引入了将一个较大的二维卷积拆成两个较小的一维卷积的做法。例如, 7× 7 卷积可以拆成 1×7 卷积和7 × l卷积。当然3x3 卷积也可以拆成 Ix3 卷积和 3 × l卷积。这被称为Factorizationinto small convolutions 思想。在论文中作者指出,这种非对称的卷积结构拆分在处理更多、更丰富的空间特征以及增加特征多样性等方面的效果能够比对称的卷积结构拆分更好,同时能减少计算量。例如,2个33代替1个55减少28%的计算量,如下图所示。
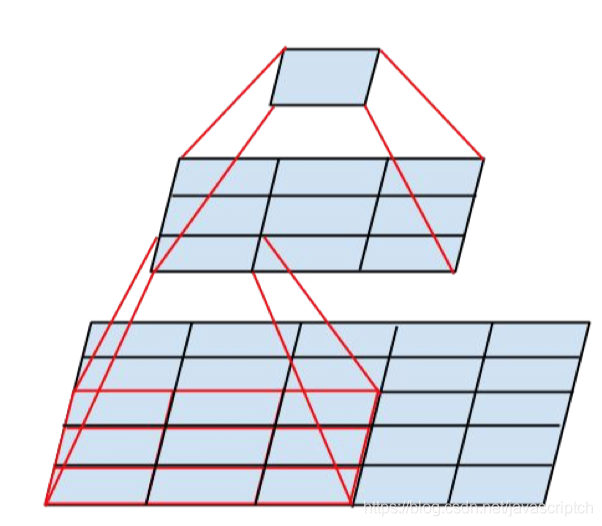
3.2 作用 1、由于 Inception 网络是全卷积的, 每一个权重都会与多处响应相关联, 计算成本的降低会带来参数量的降低. 这意味着通过恰当的因式分解(factorizationinto convolutions), 作者可以得到更多解耦的参数, 从而可以带来更快的训练速度。
2、论文中也提了辅助分类器的效用。带有辅助分类器和不带辅助分类器的两个网络,在模型达到较高精度以前,他们的性能看起来是差不多的。但是当到了训练后期,带有辅助分支的网络开始超越没有任何辅助分支的网络,进而达到更高的精度。
小波变换
小波变换的原理
先介绍相似度
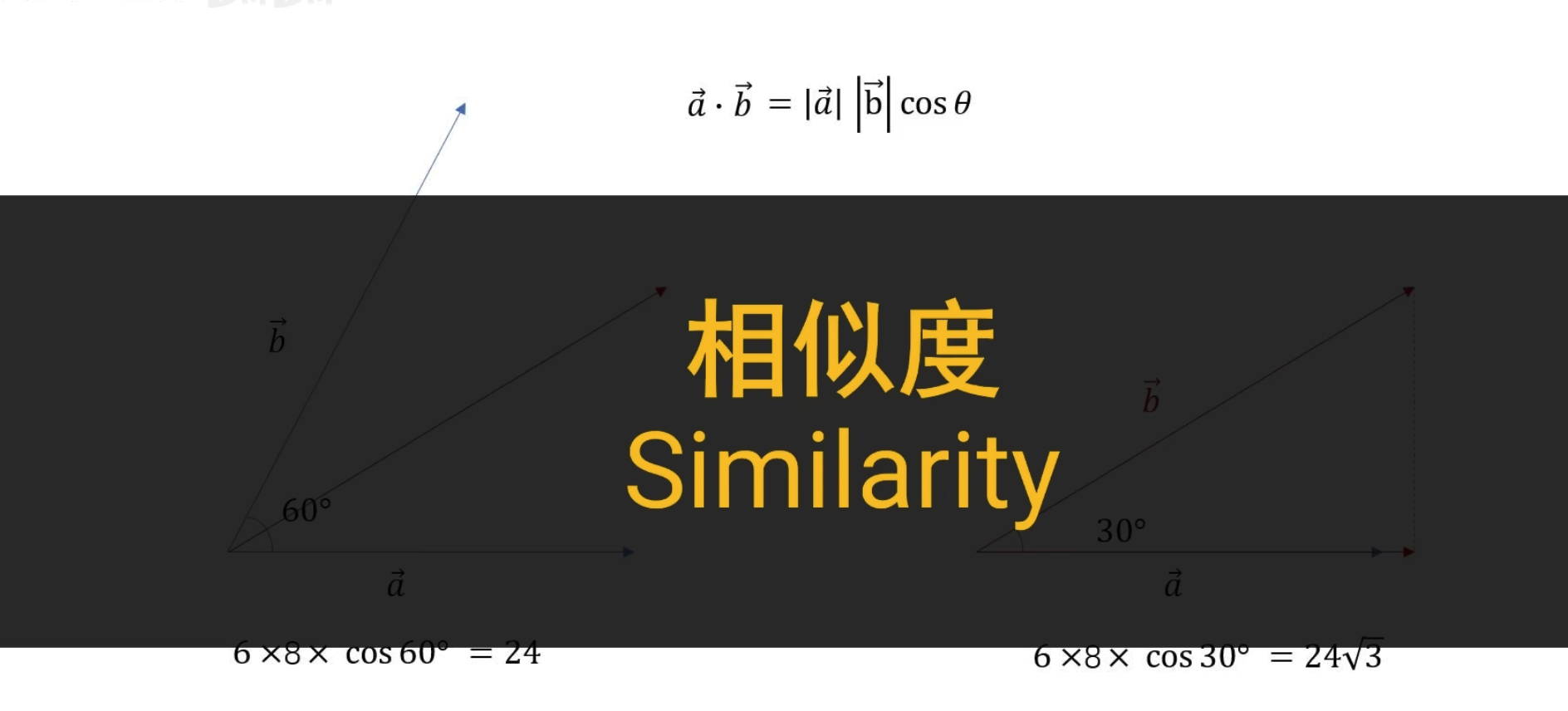

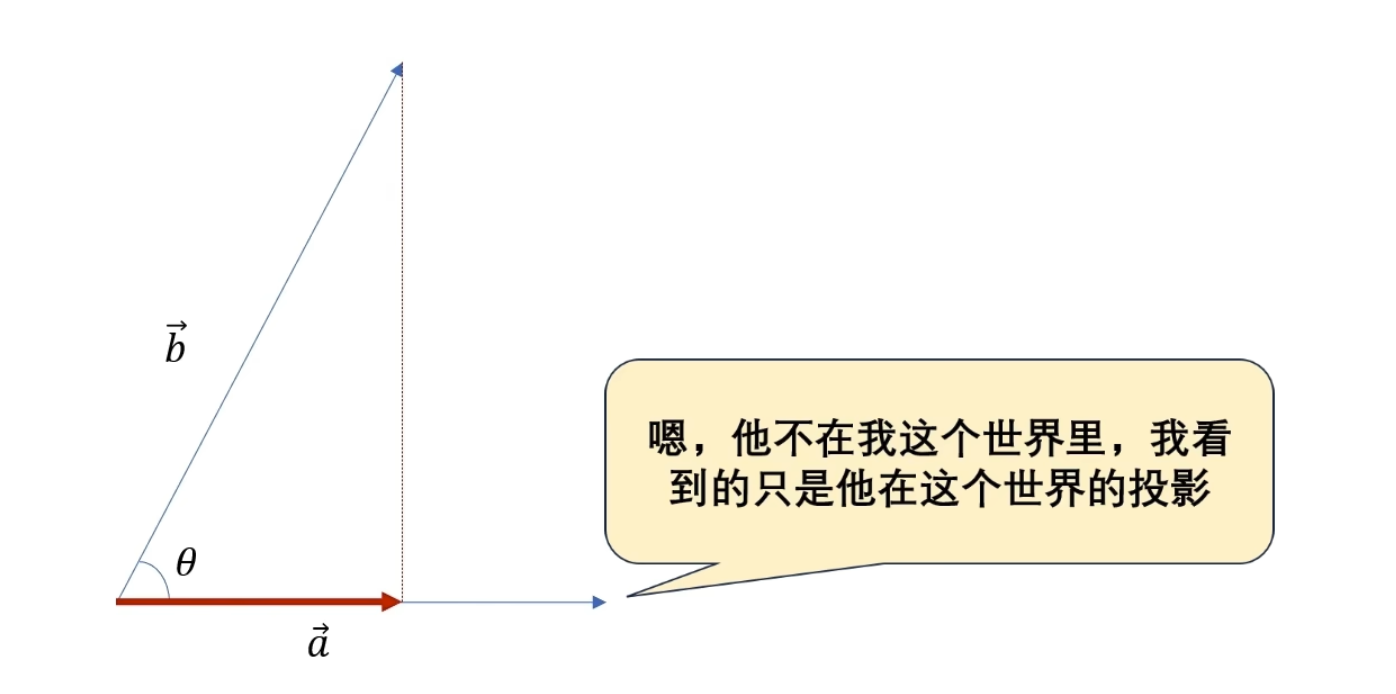
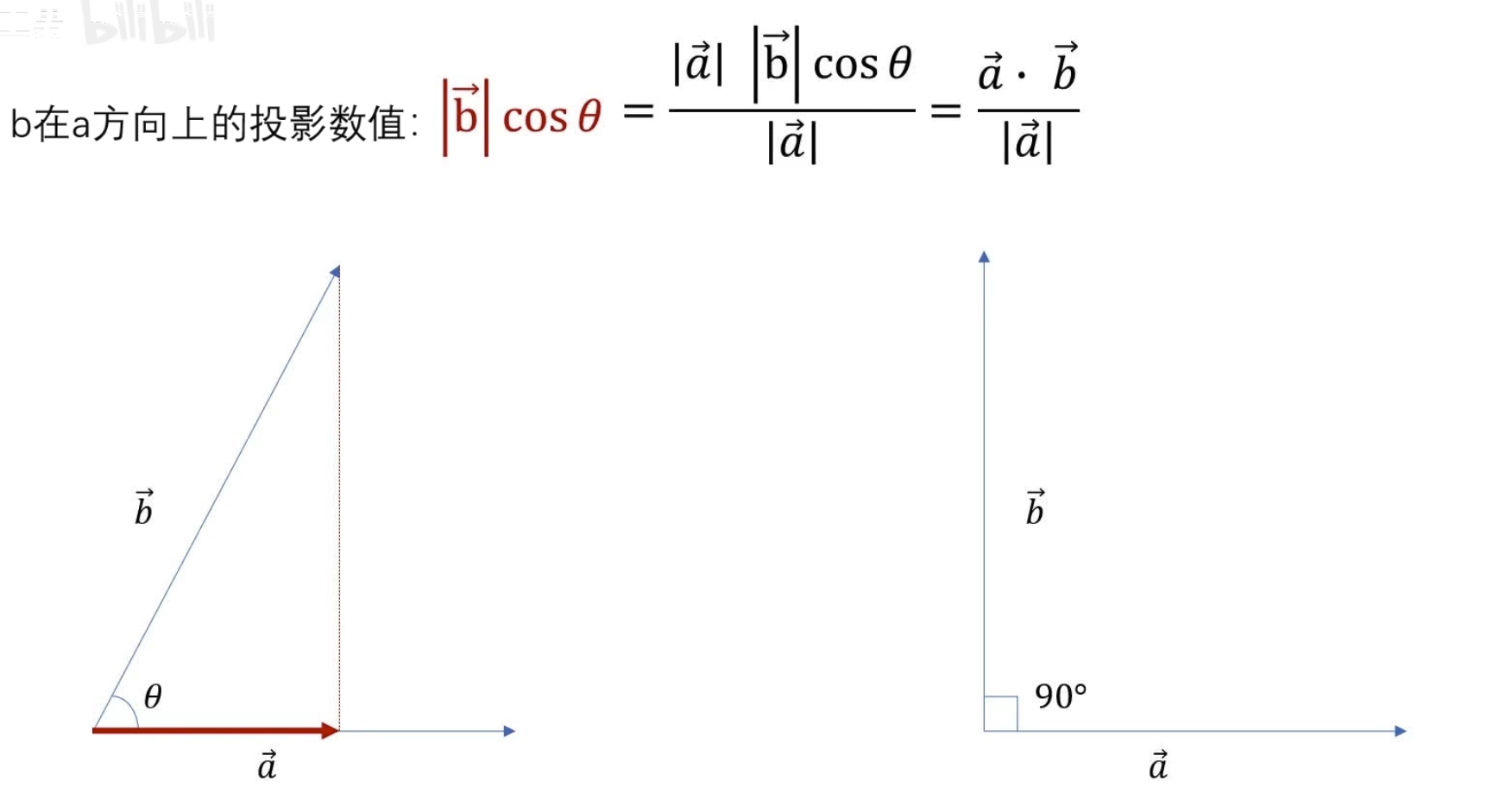
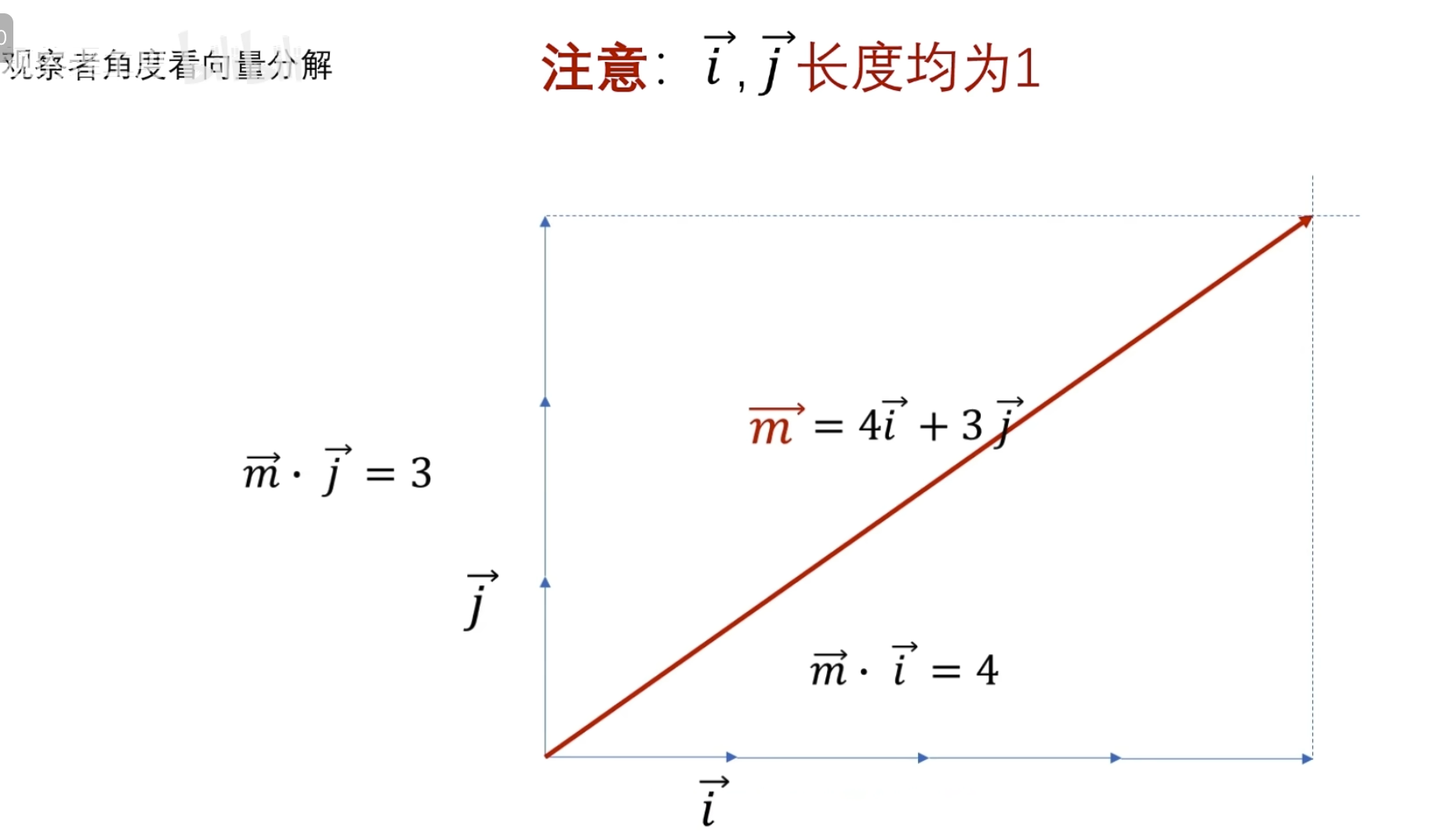

归一化的作用:

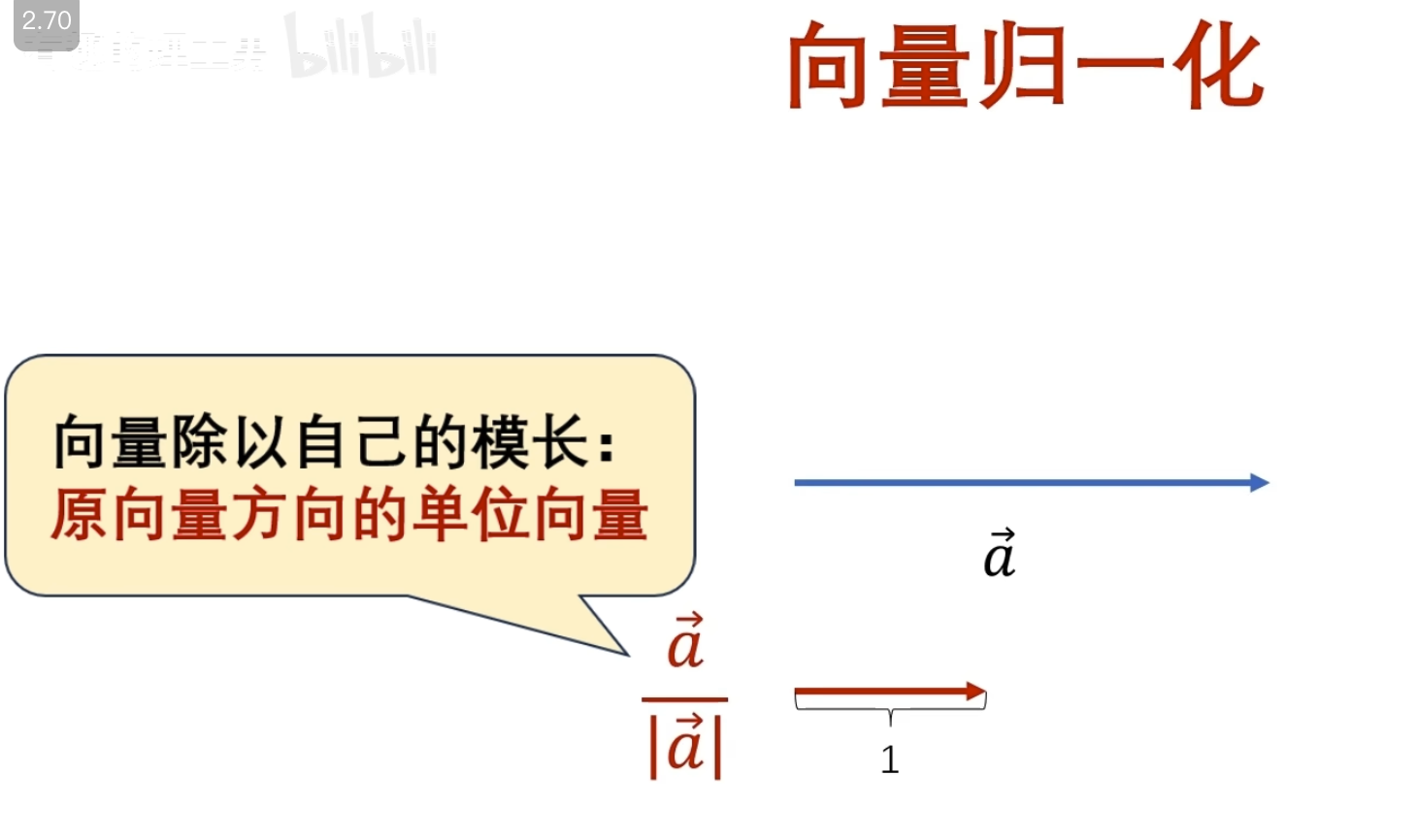
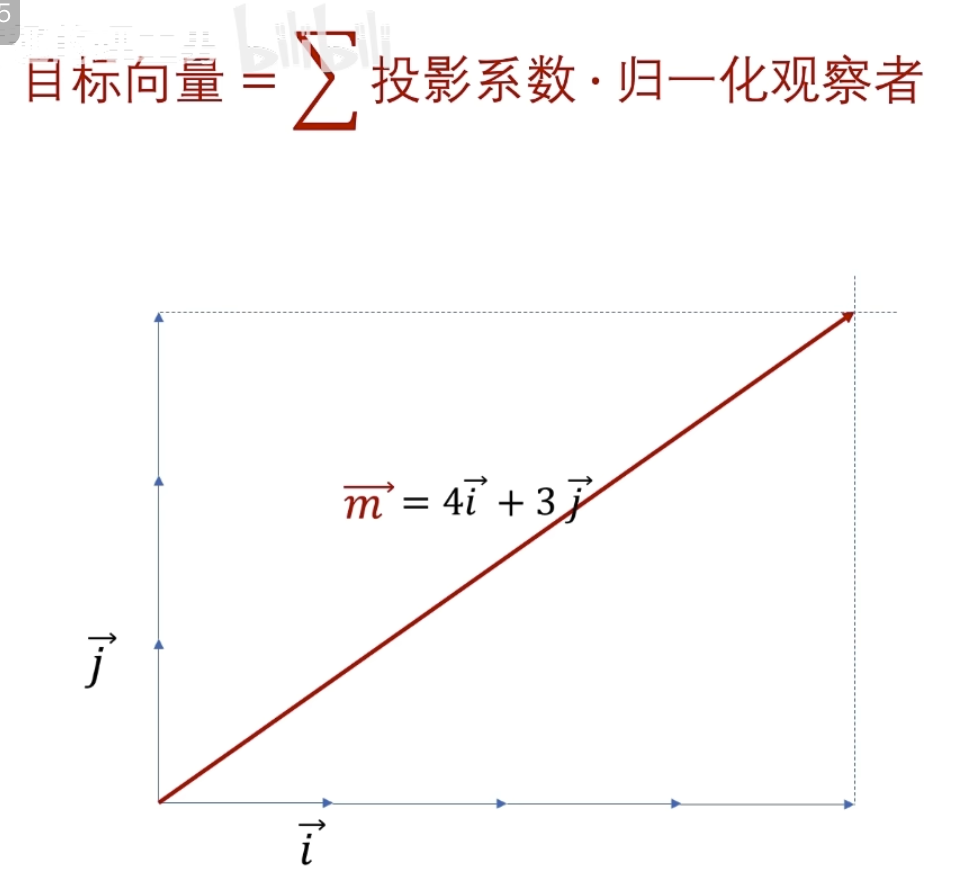
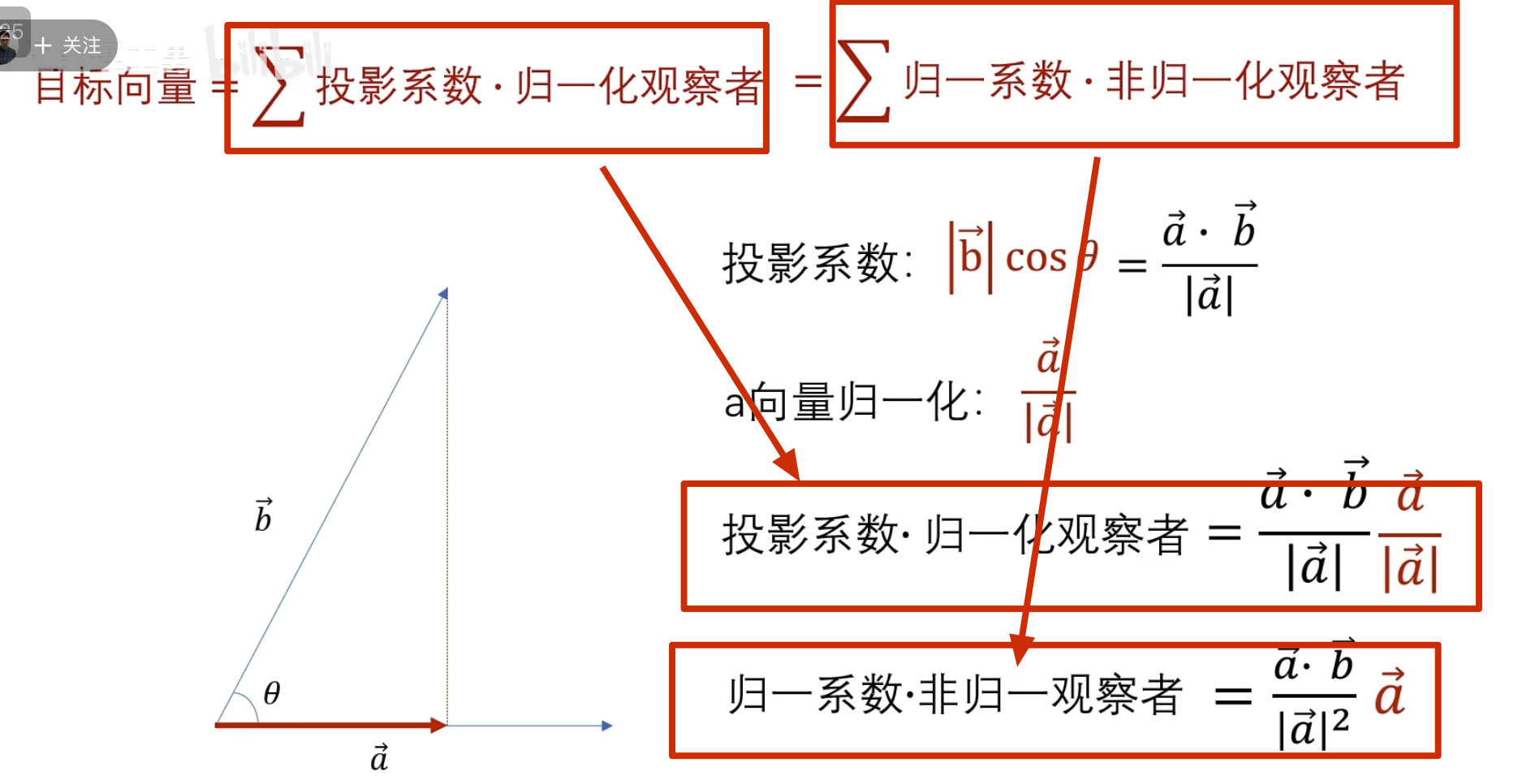


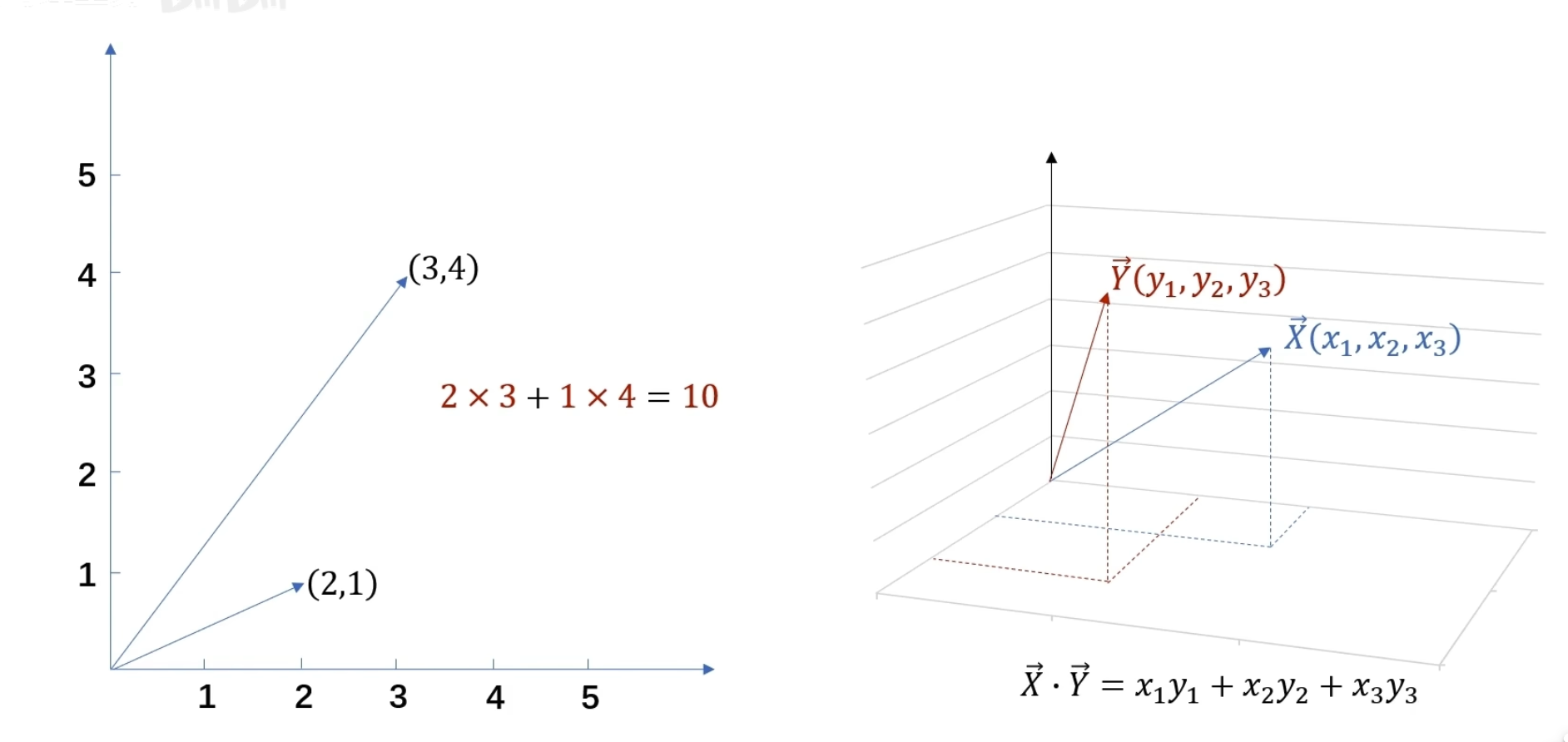


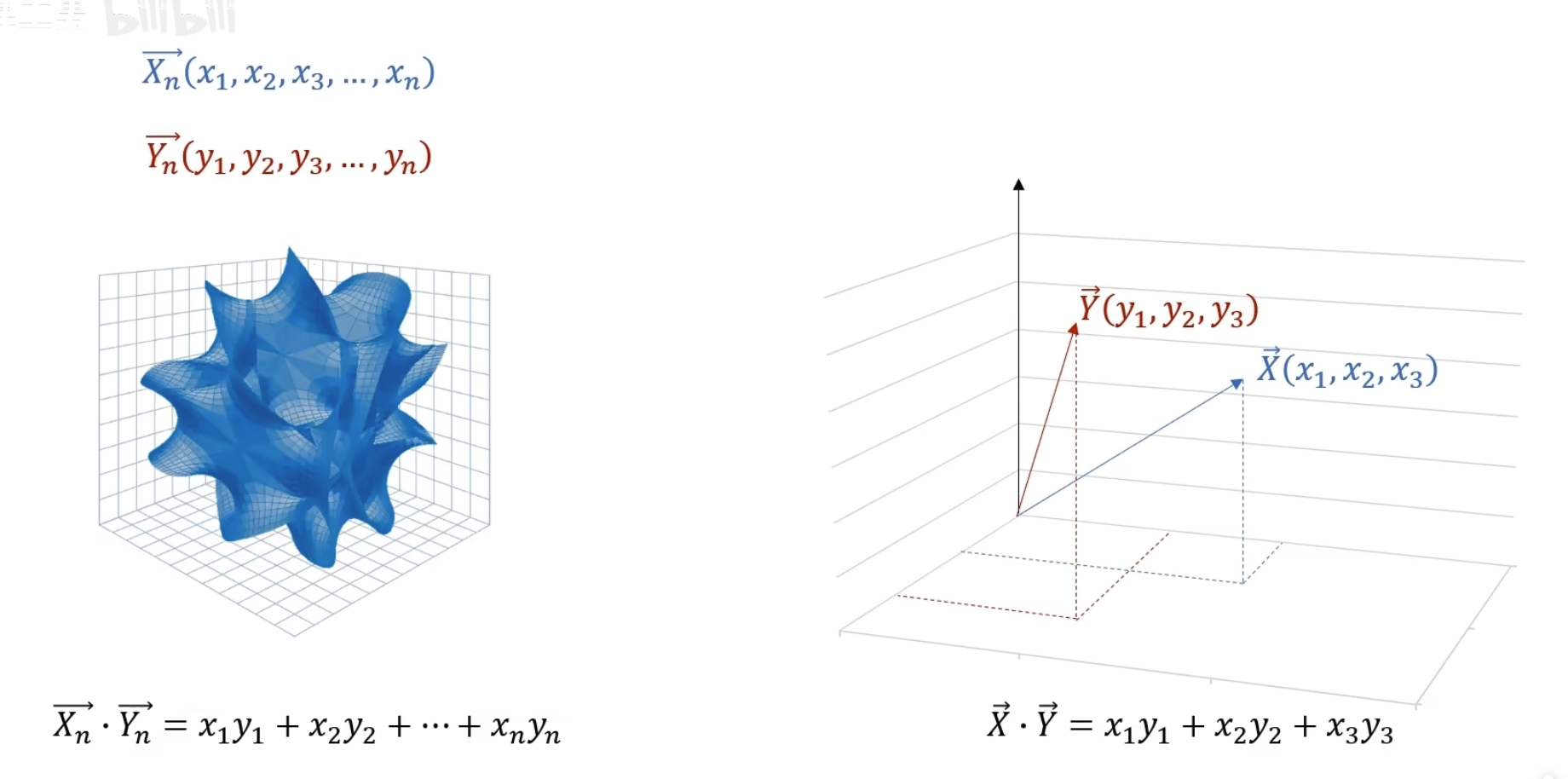
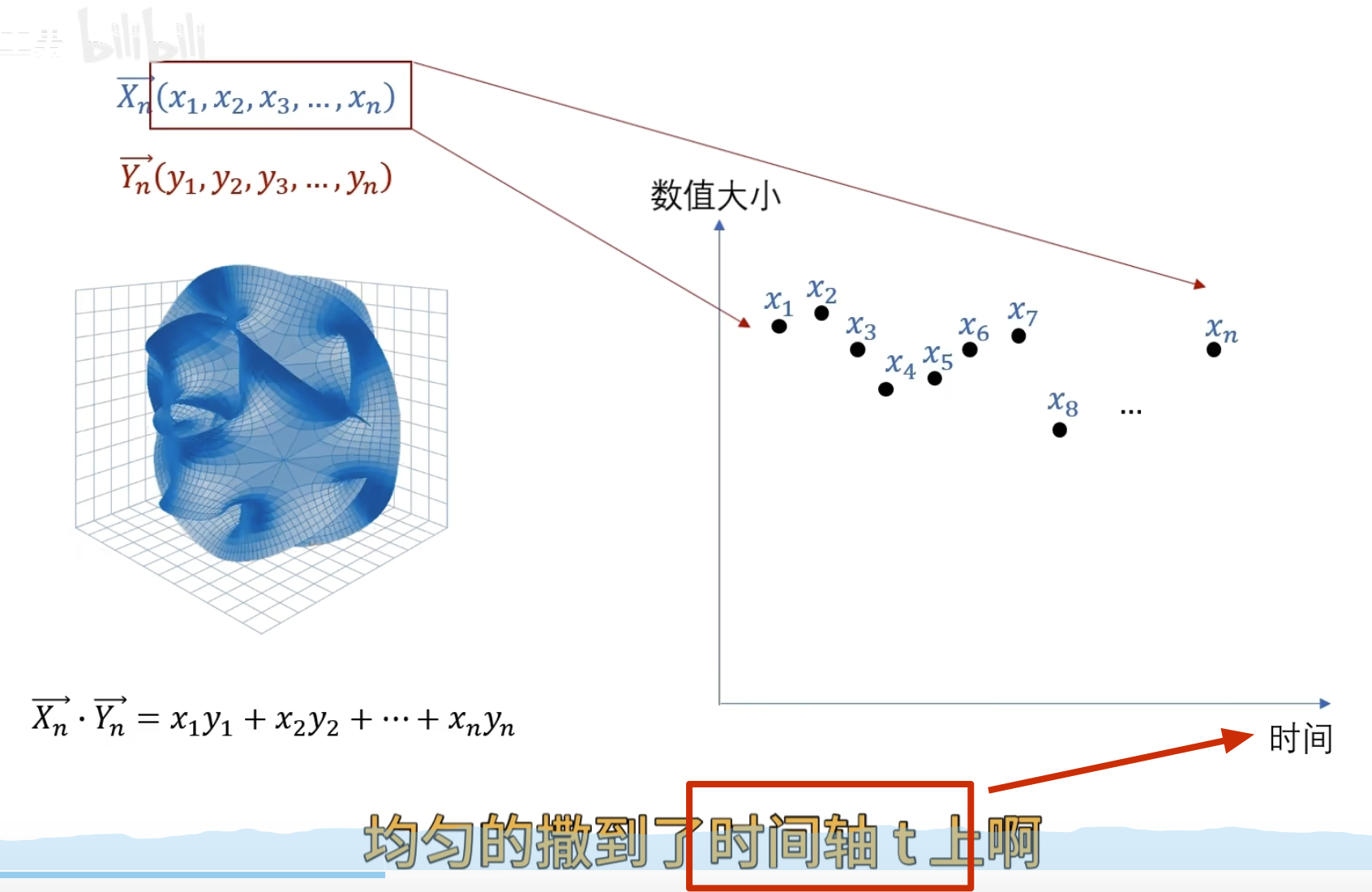 当 n 越来越大直到无穷的时候
当 n 越来越大直到无穷的时候
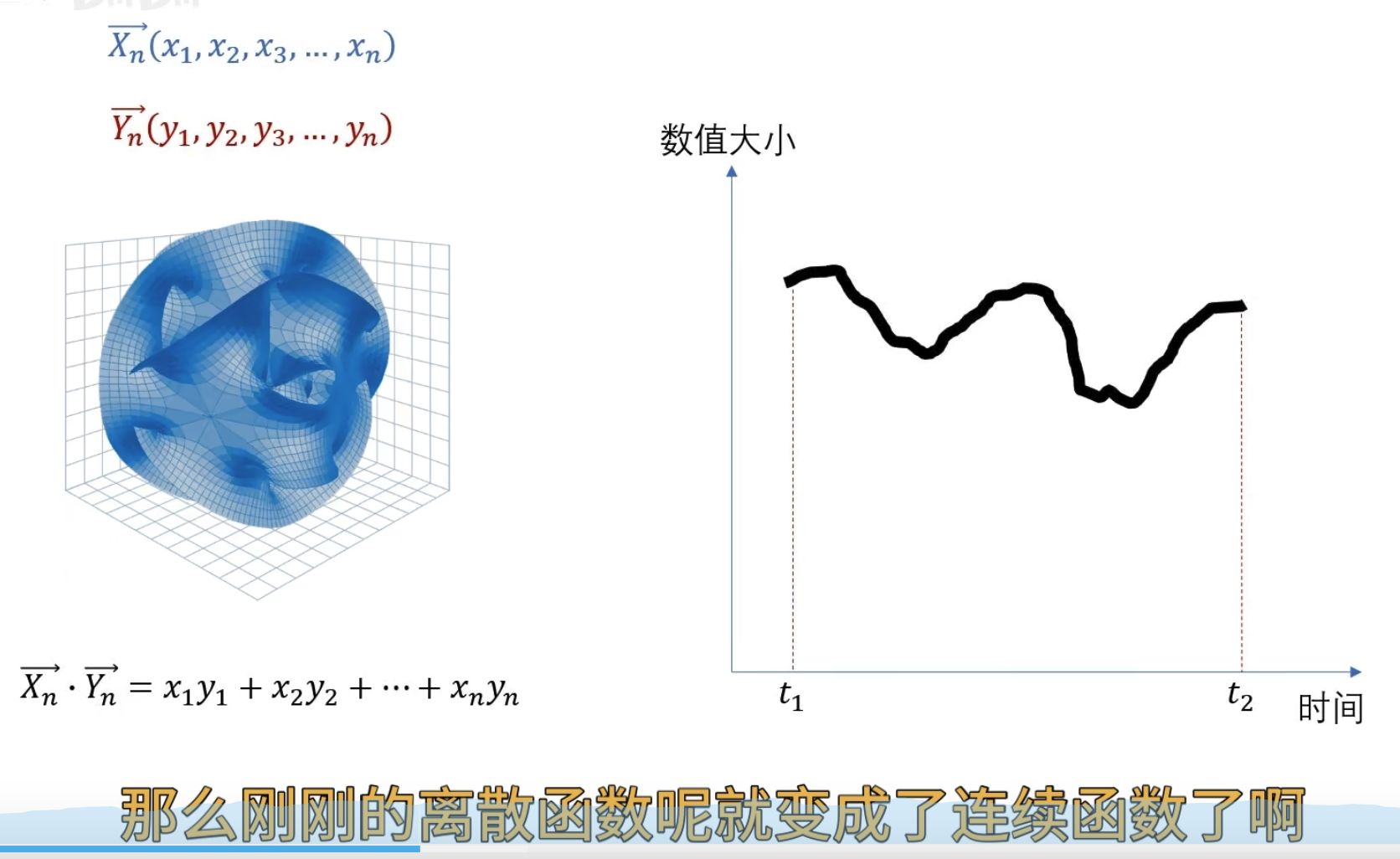
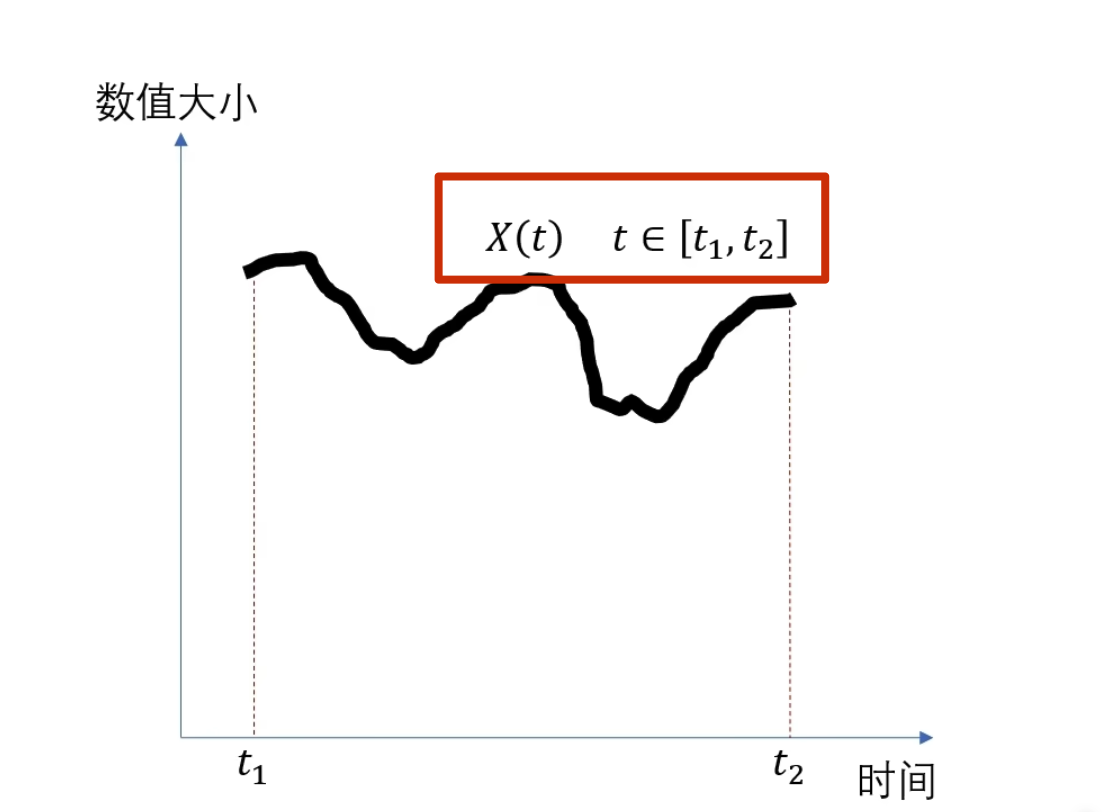
可以讲一个连续函数看成一个连续无穷维向量

求点乘
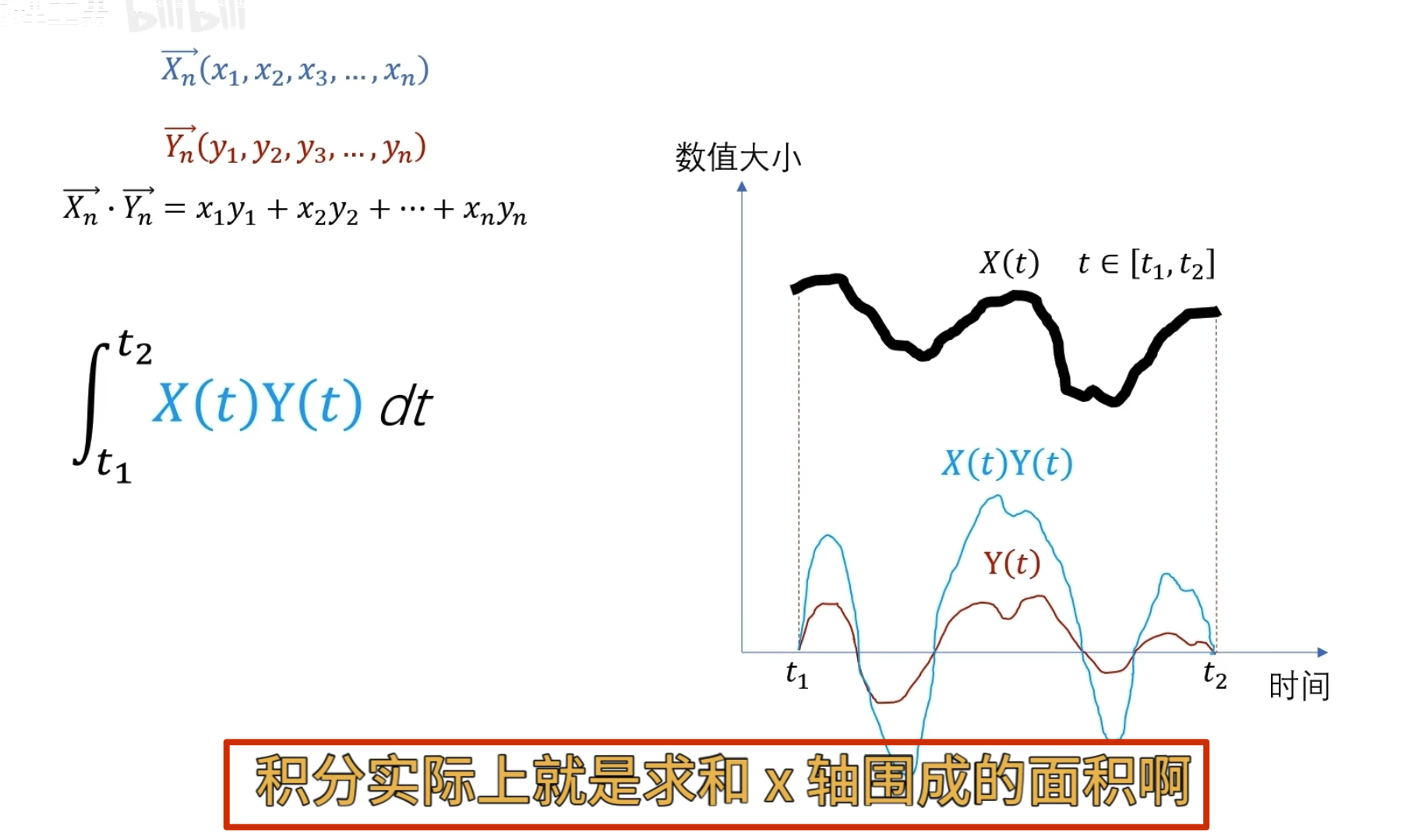
可以认为 sin x和 cos 2x 在-pi 到 pi 的范围内一点都不像(点乘为 0)
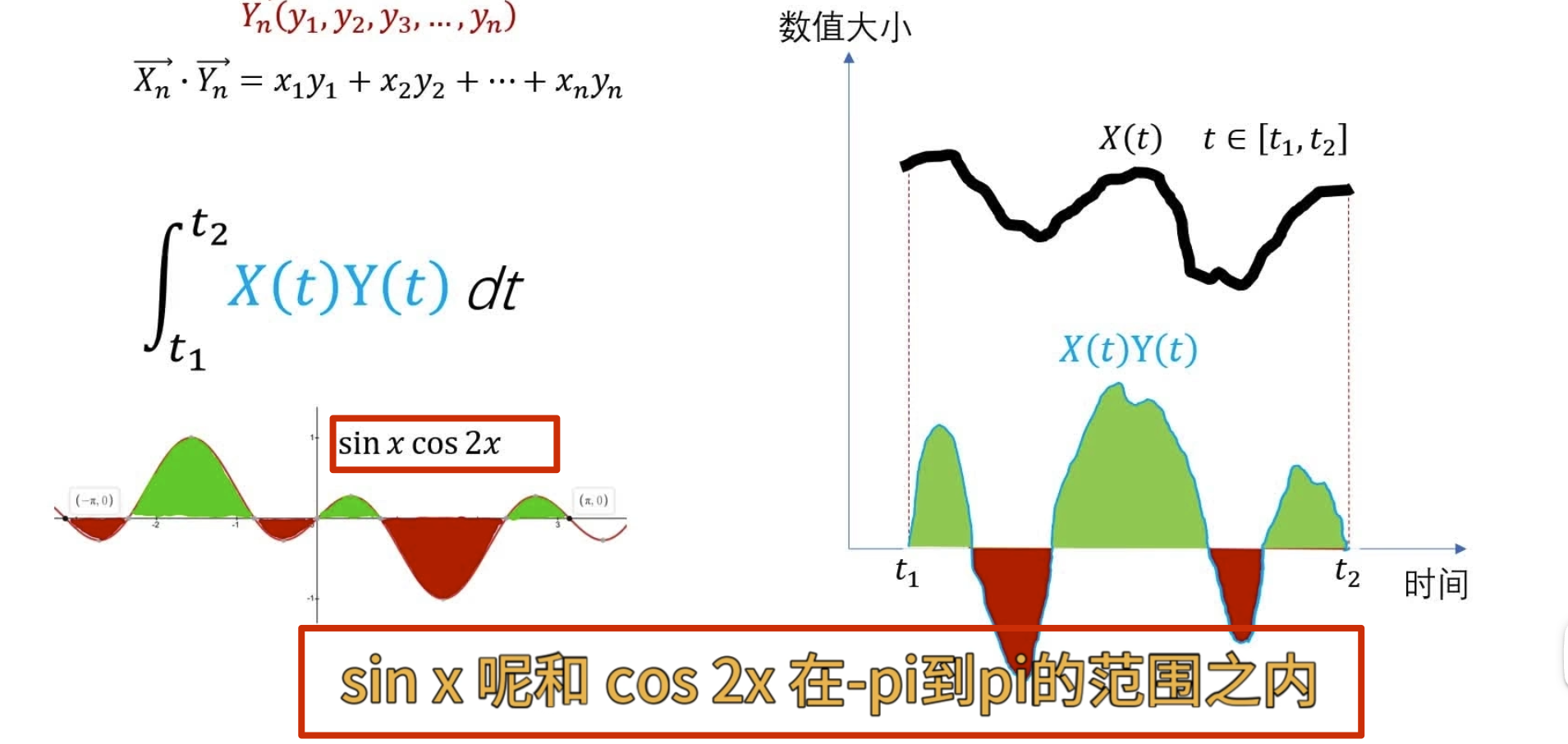
这就是两个连续函数点乘的定义


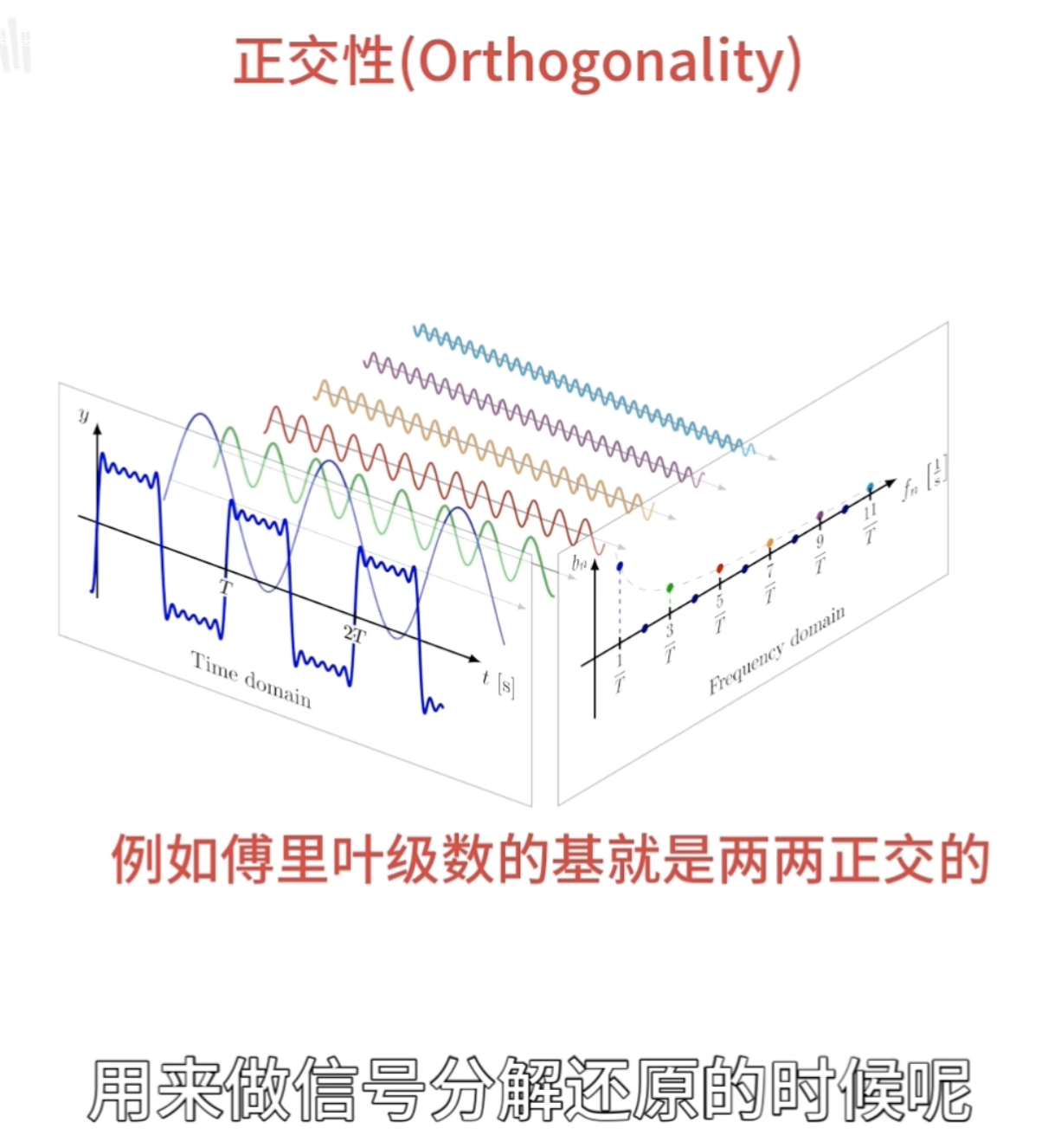
一、基
傅立叶变换和小波变换,都会听到分解和重构,其中这个就是根本,因为他们的变化都是将信号看成由若干个东西组成的,而且这些东西能够处理还原成比原来更好的信号。那怎么分解呢?那就需要一个分解的量,也就是常说的基,基的了解可以类比向量,向量空间的一个向量可以分解在x,y方向,同时在各个方向定义单位向量e1、e2,这样任意一个向量都可以表示为a=xe1+ye2,这个是二维空间的基,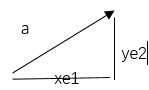


可以看到目标函数到自己频率的世界中的投影(目标函数和观察者的相似度是多少 )
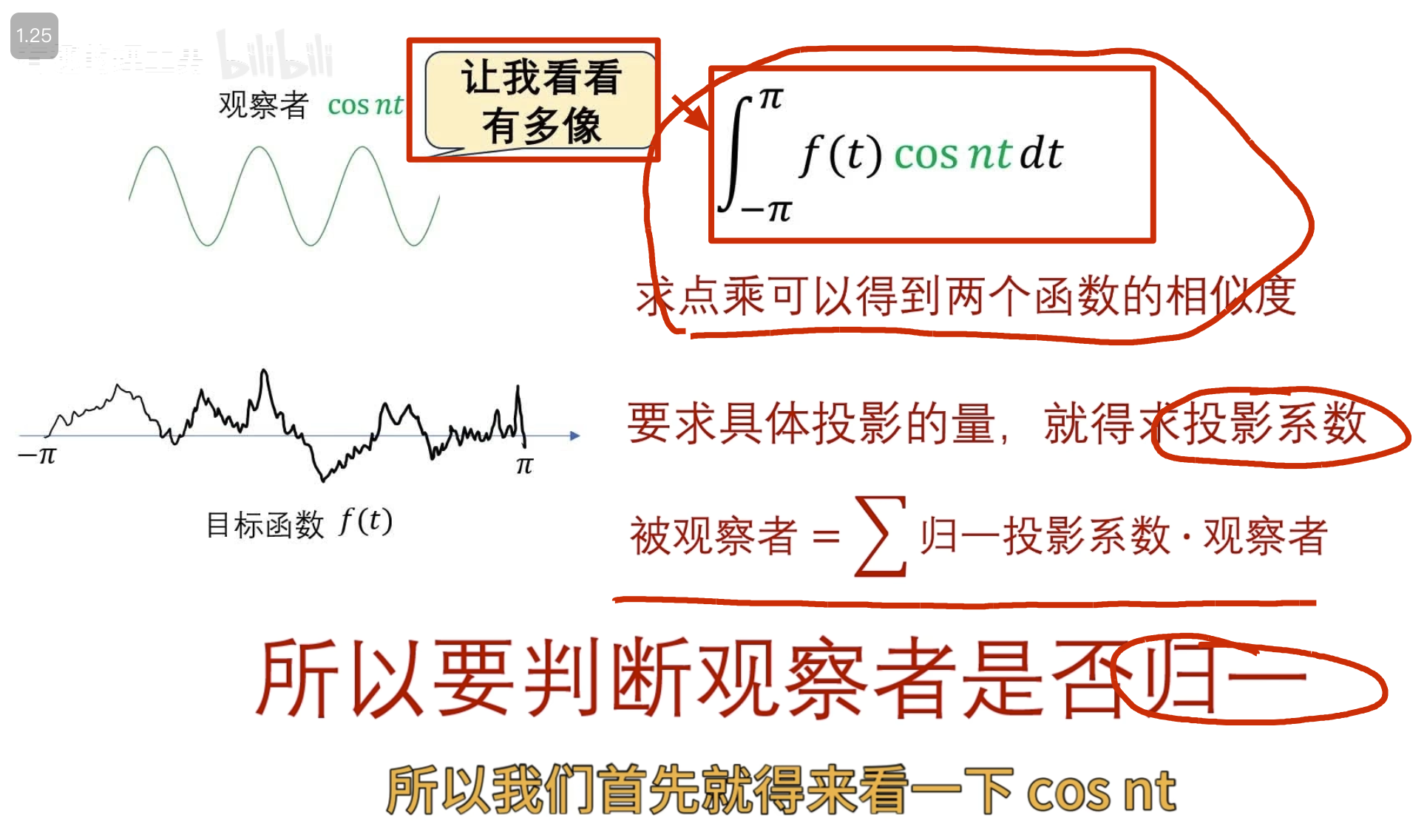
这里已经讲过了要么观察者是归一的,要么投影系数是归一的
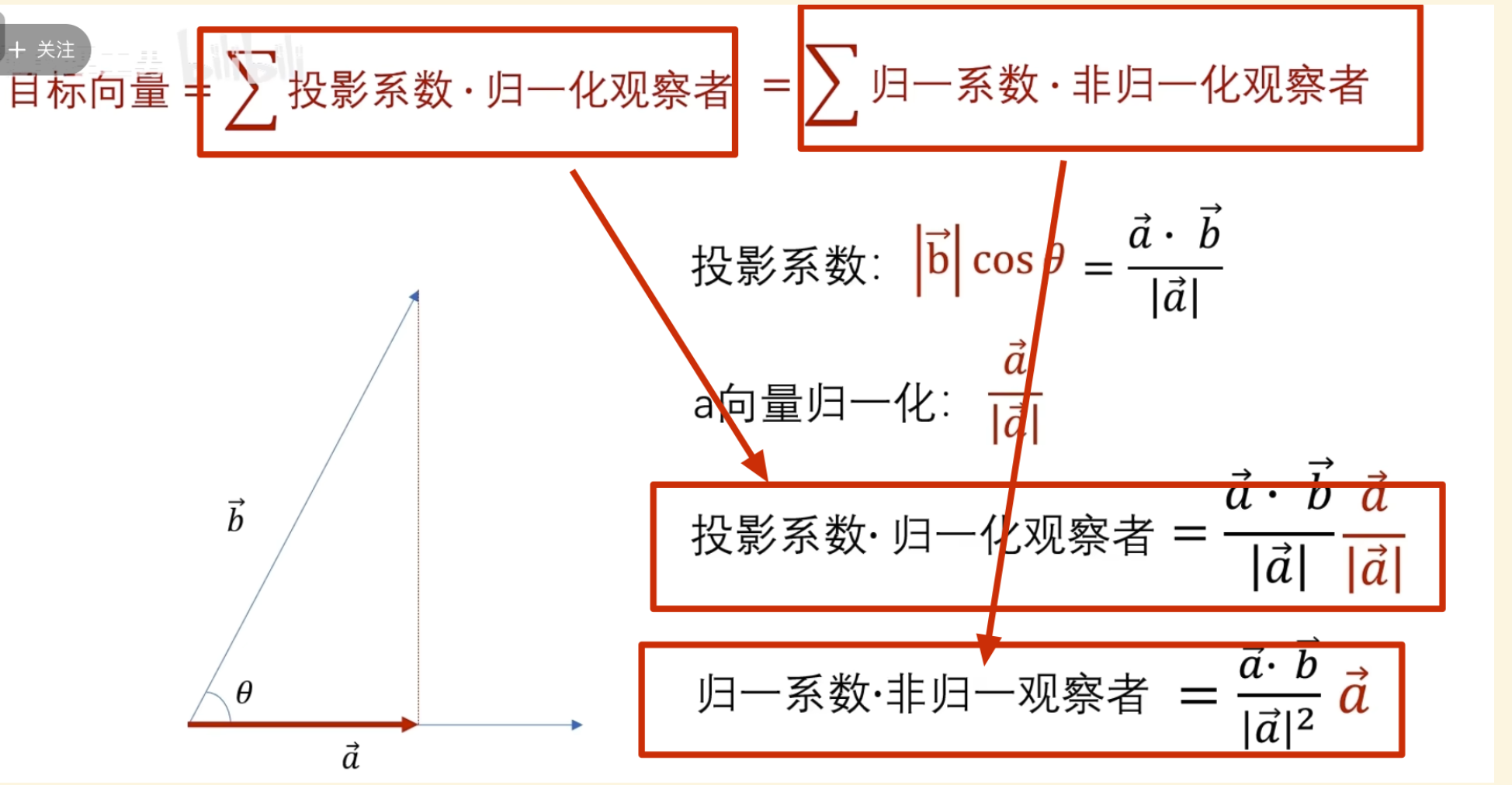

其实对于连续函数一般不叫模长,而叫 2-范数

这里显然 cos nt 未归一,所以需要对投影系数进行归一

所以最终得到的归一投影系数(这就是我们之前学的傳里叶级数求A n 的公式,对应到不同频率基的振幅 )

再进一步到傅里叶变换的负指数形式

思想是一样的,只是观察者由余弦函数变成了下面的(观察者由实数域拓展到了虛数的复数域)
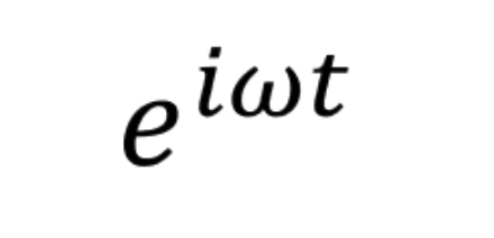
\(w\)越大,旋转越快 (不过观察者旋转的半径都是 1,即观察者已经是归一化的了)

这是一个复数
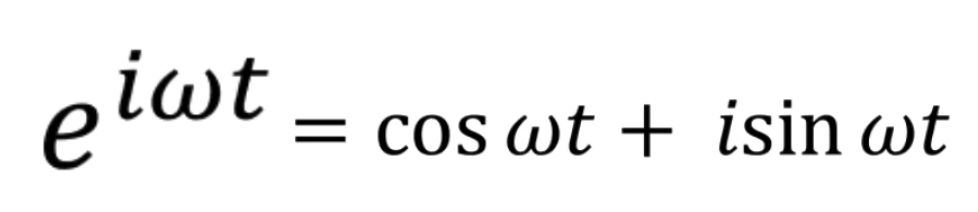
对于复数,计算模长有两个公式,所以计算虚函数的模长(应该也叫 2-范数)的公式也有变化 ,点乘计算相似度的公式也有变化
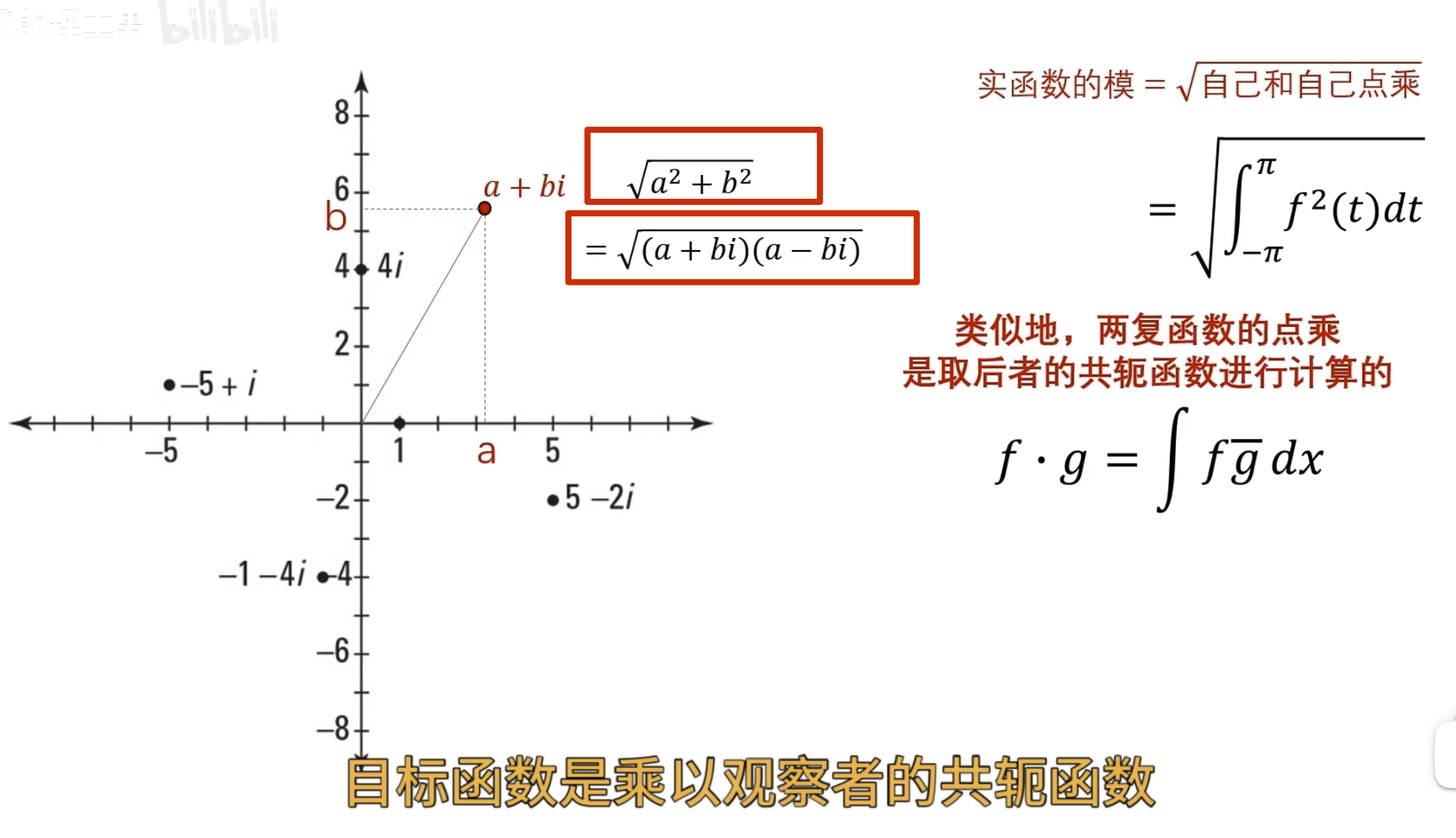
点乘计算目标函数和观察者的相似度

上面已经讲了,观察者旋转半径都是 1,所以是已经归一的了,只是旋转的快慢不同

当然用定义也能验证是已经归一化了的
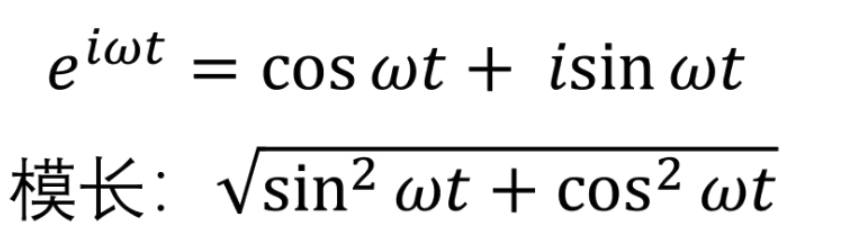
总结连续函数相似度计算公式如下(也就是常用的连续函数的傅里叶变换公式 )
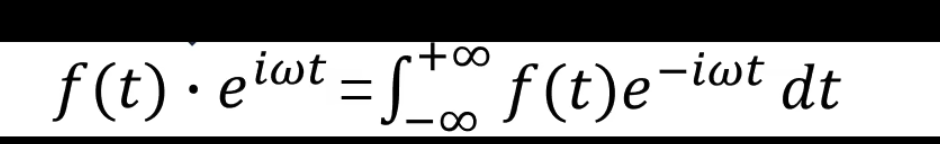
我们积分出来的结果通常是一个关子频率\(w\)的复凾数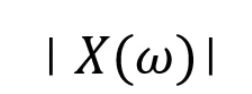 ,而这个复函数的模啊就加个绝对值就可以㻫解为前们前面所说过的投影数,也就是该频率下的震动的幅度
,而这个复函数的模啊就加个绝对值就可以㻫解为前们前面所说过的投影数,也就是该频率下的震动的幅度
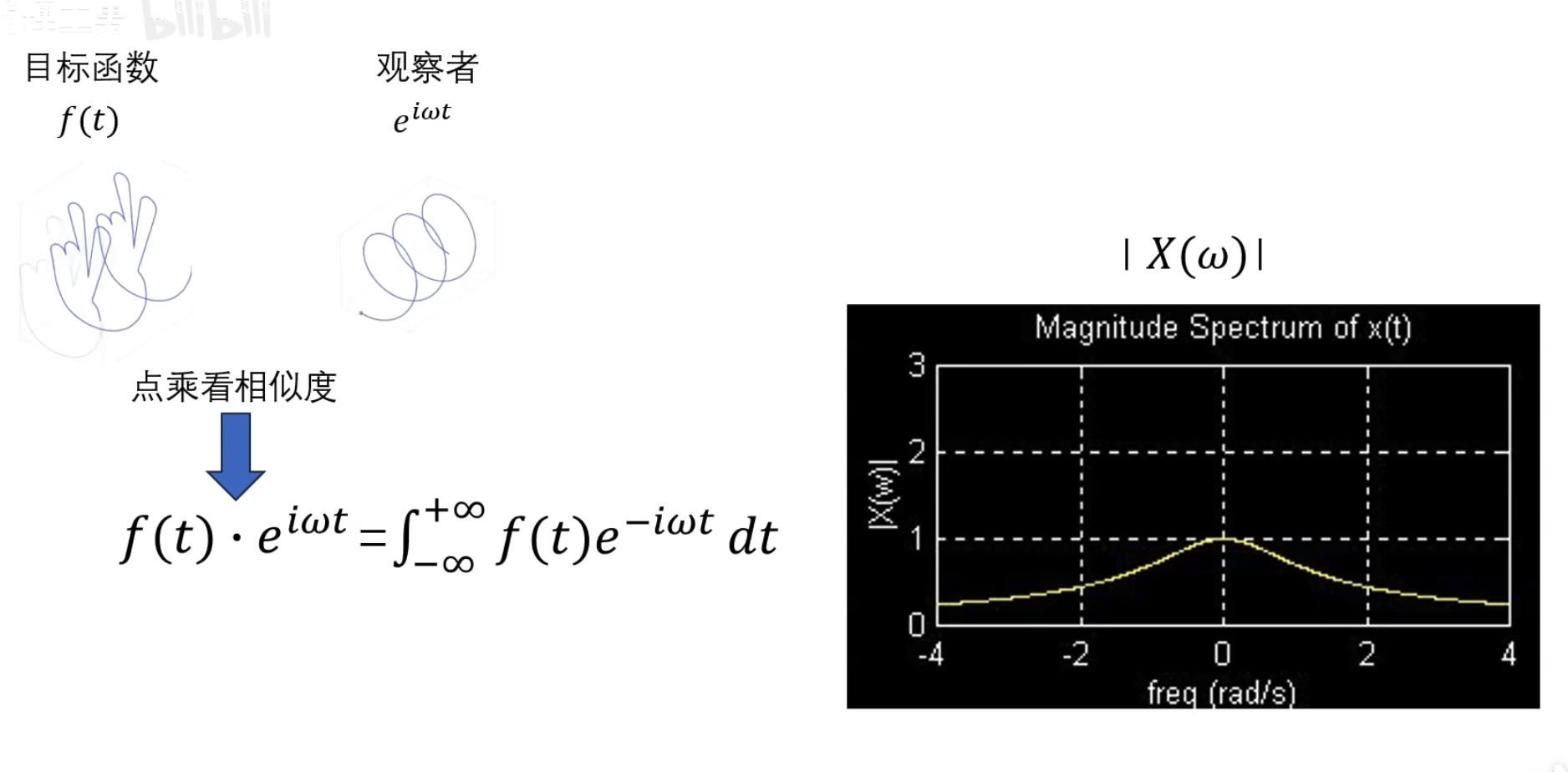
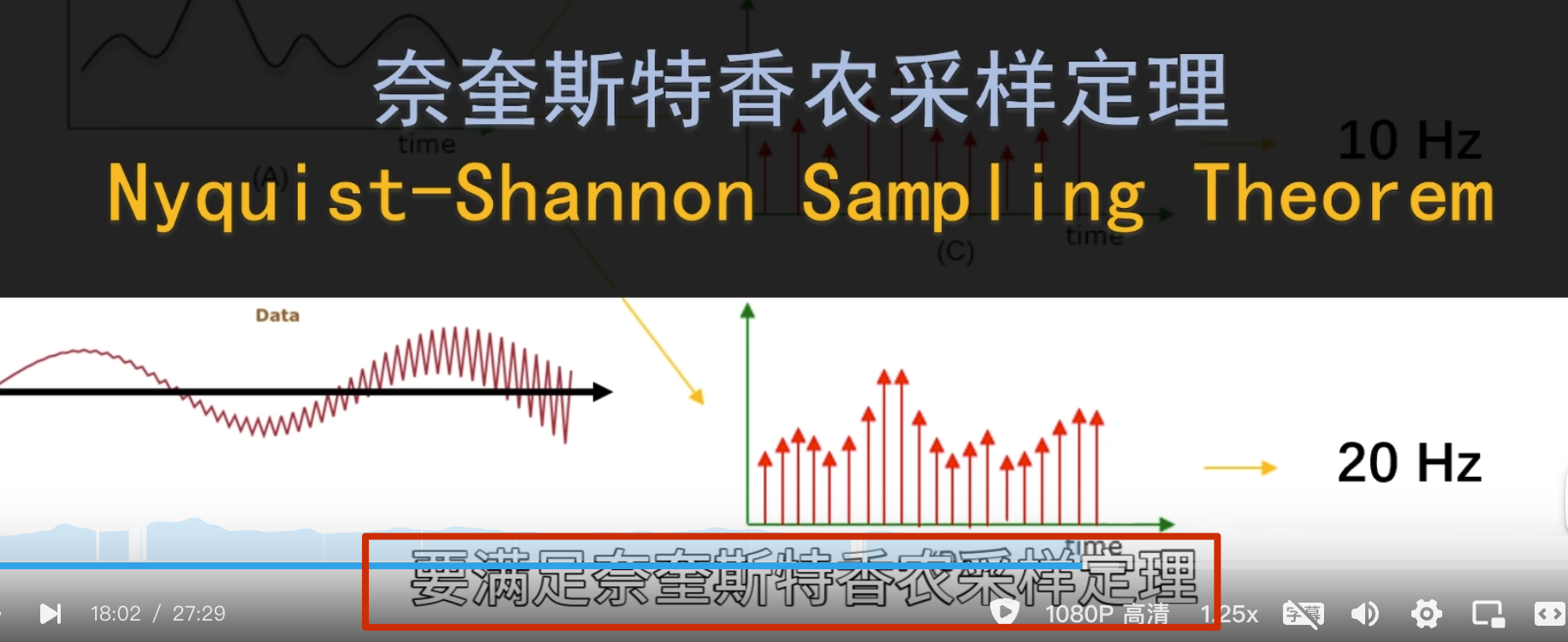
以上就是傅里叶变换,但是事情并非我们想象的那么美好 ,问 题呢就出现在了观察者的身上
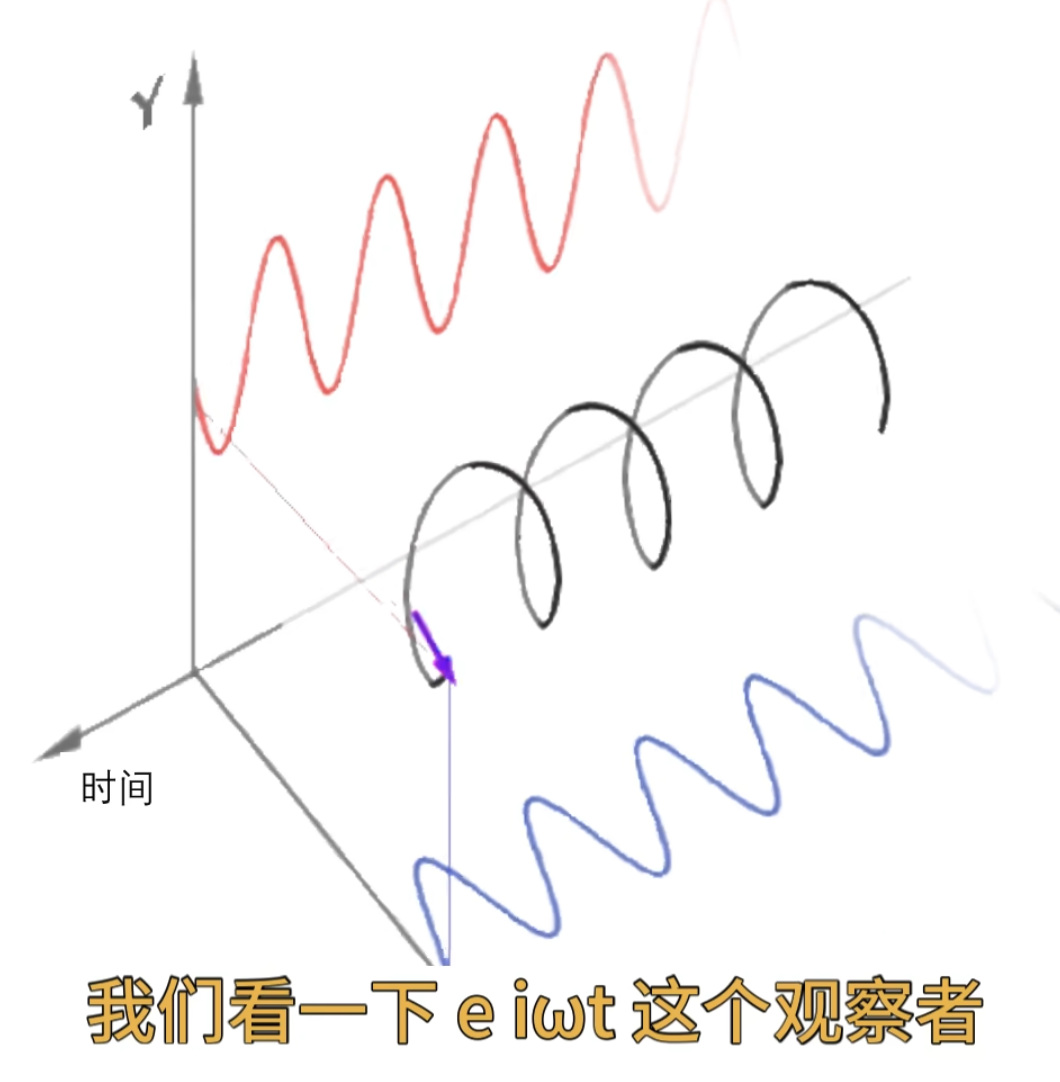
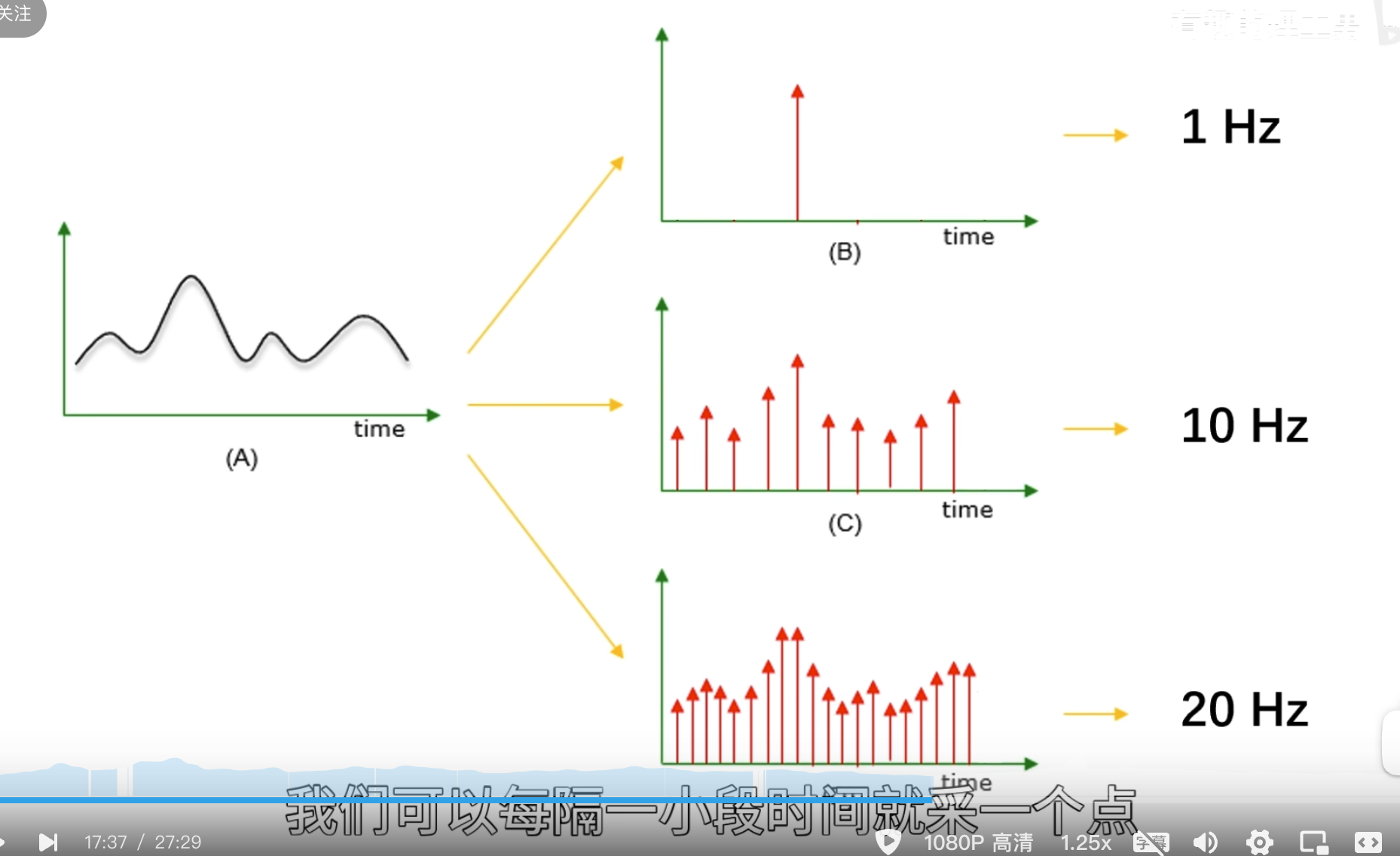
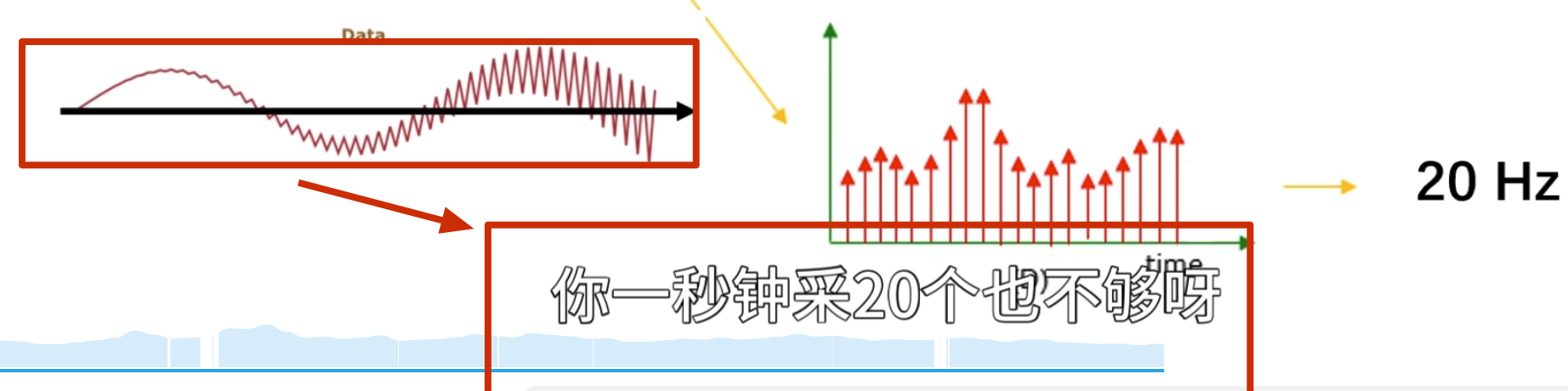
观察者\(e^{iwt}\)它在时间轴上是无穷无尽的,如果我们的目标函数是长这样的,在前面一小段振动频率很高,而后面时间的振动几乎都是低频的振动
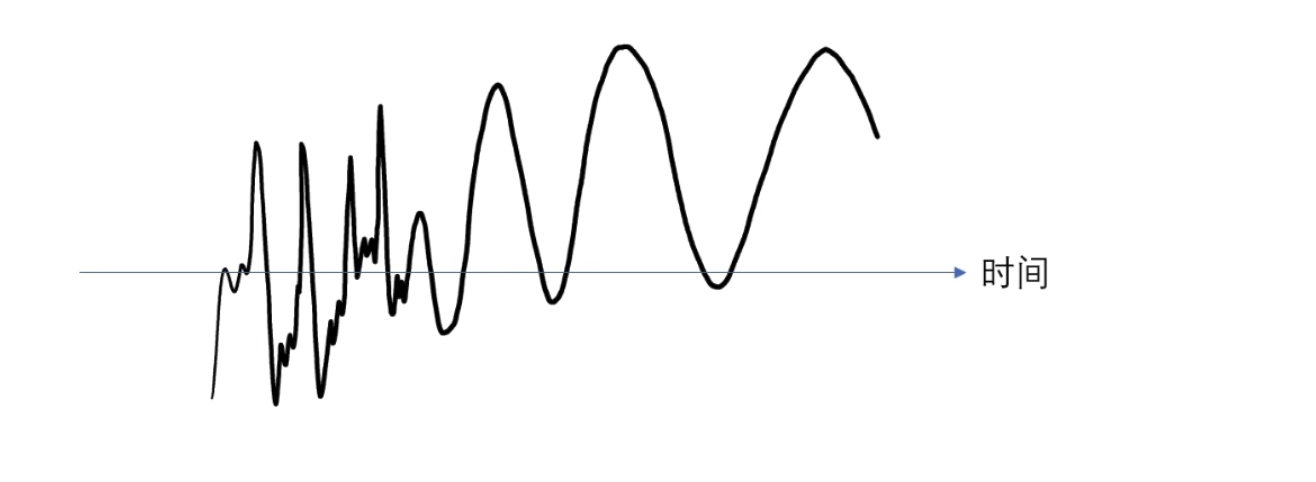
这个时候使用一个高频的观察者观察它,问两个函数的相似度
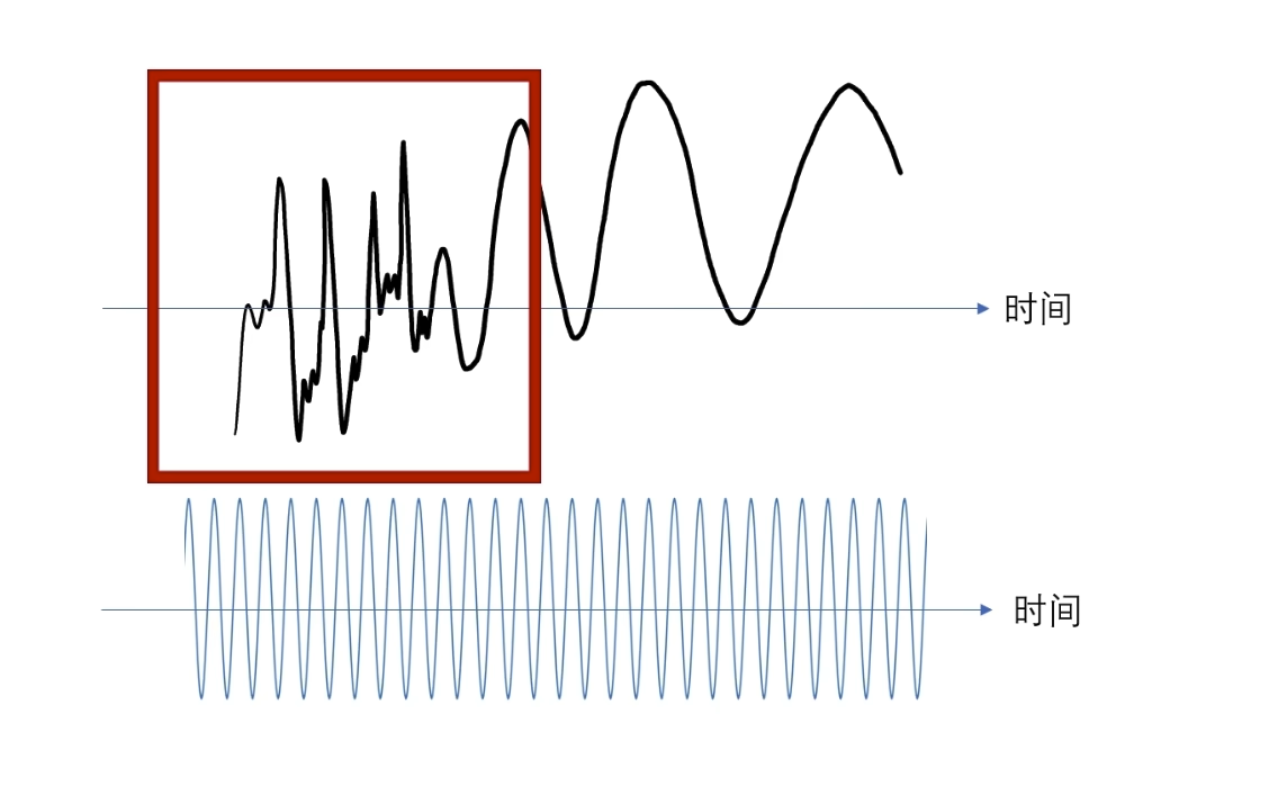
问哪个时间段像?它回答不了因为对于这个观察者来说它是在整个时间轴展开的,无穷无尽的, 观察者 一变呢就是整个时间轴一起变的啊
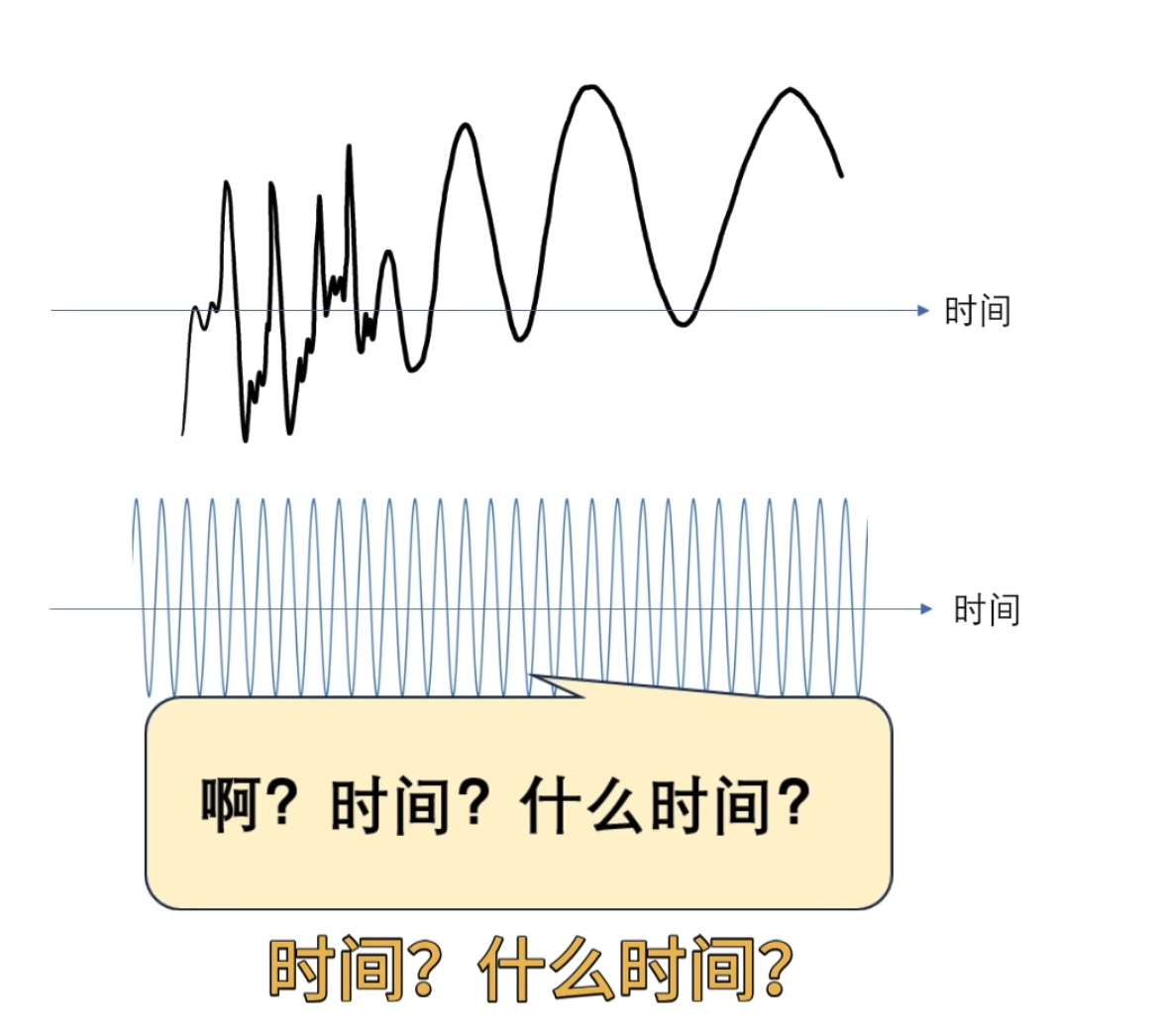
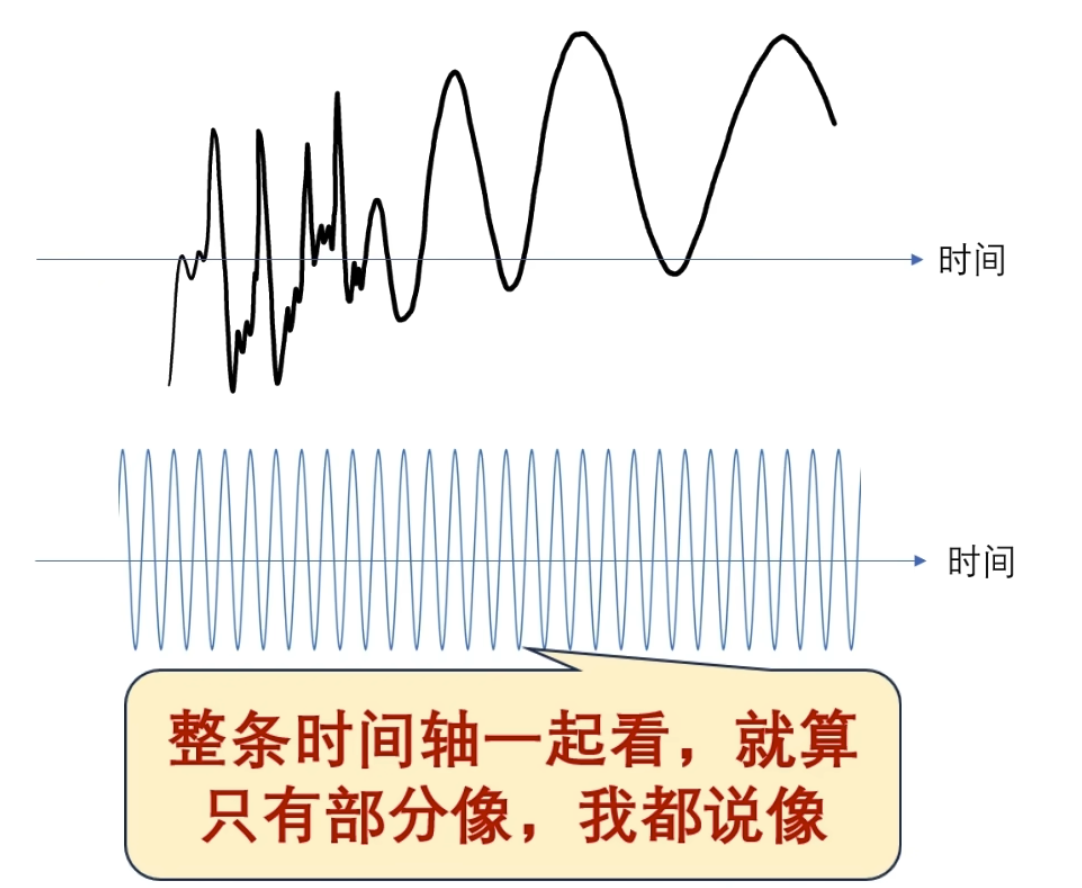
所以尝试改造观察者

观察者局域化,这个褒減过的观察者,在时间轴上就不再是无穷无尽的啦
,它其实呢就是把它给局域化了哈 ,我们可以把这个观察者写作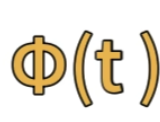
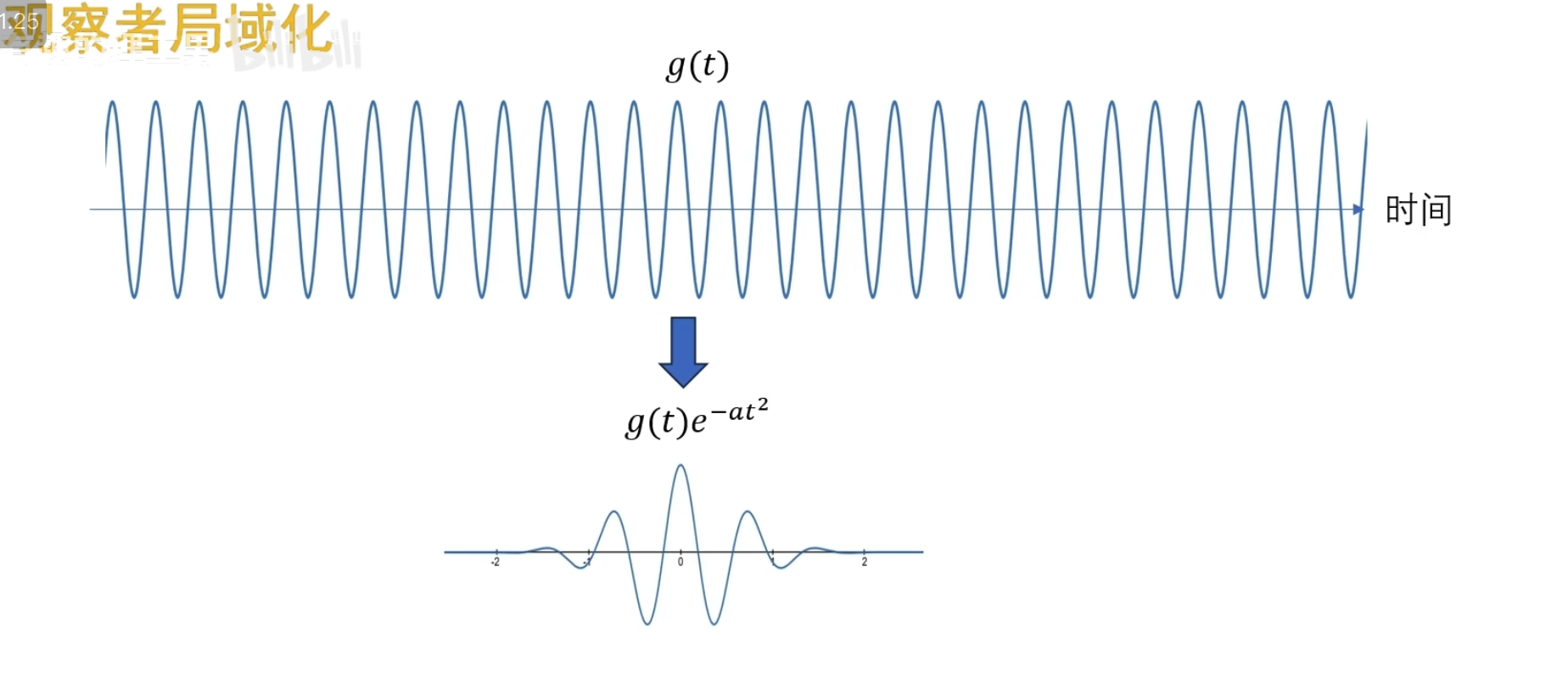
这个时候我可以让这个观察者顺着时间轴去巡逻,再把不同的时闻点观察剄的结果 反馈给我
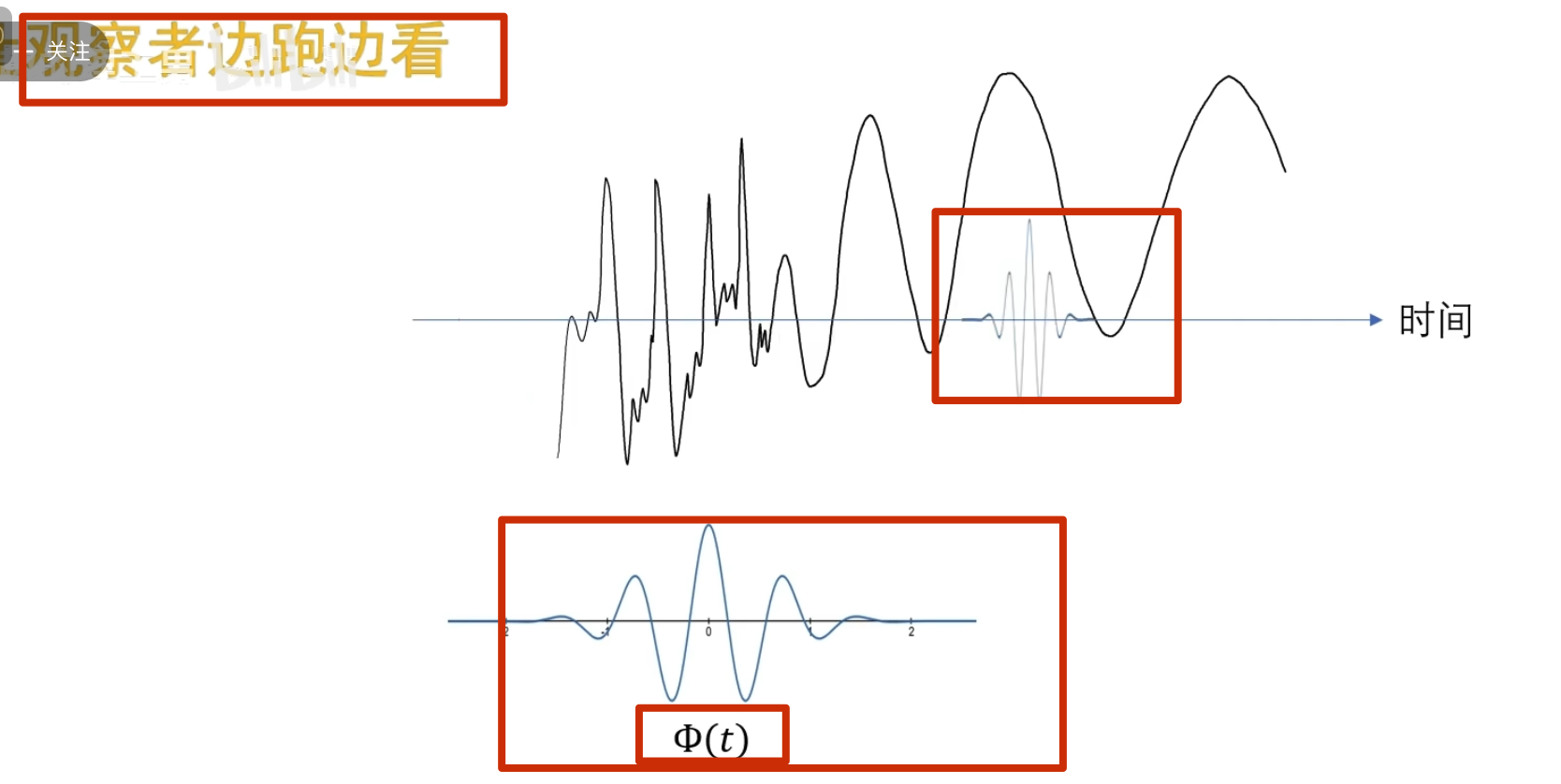
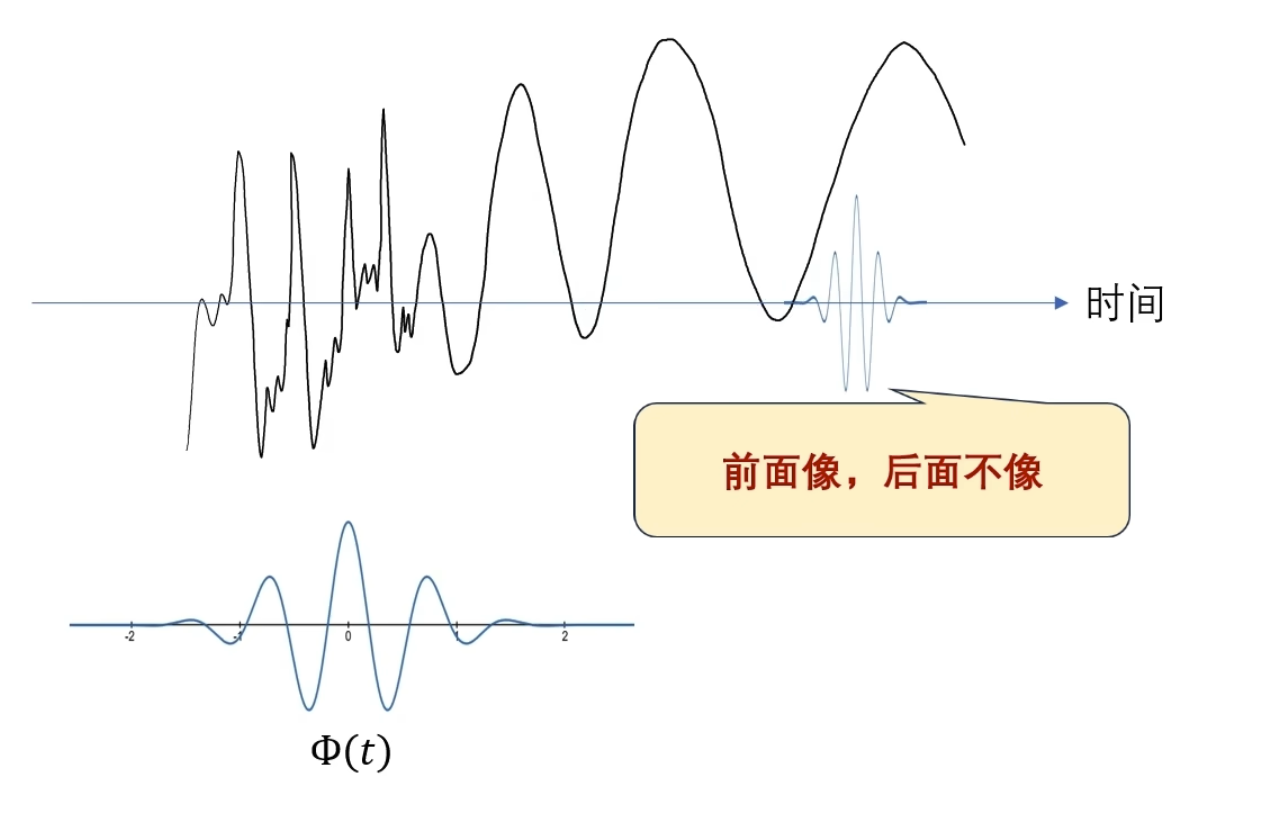
怎么实现巡逻呢?——函数的平移,b 为平移因子
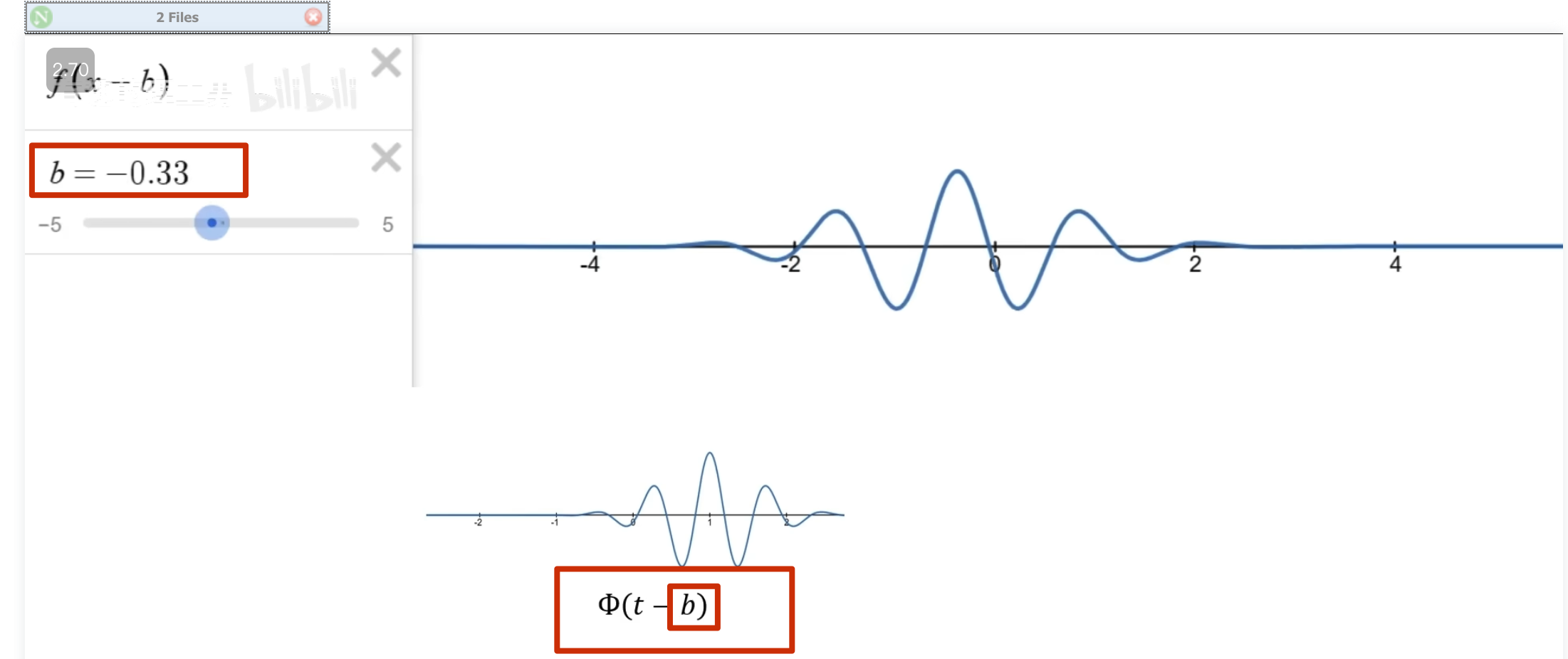
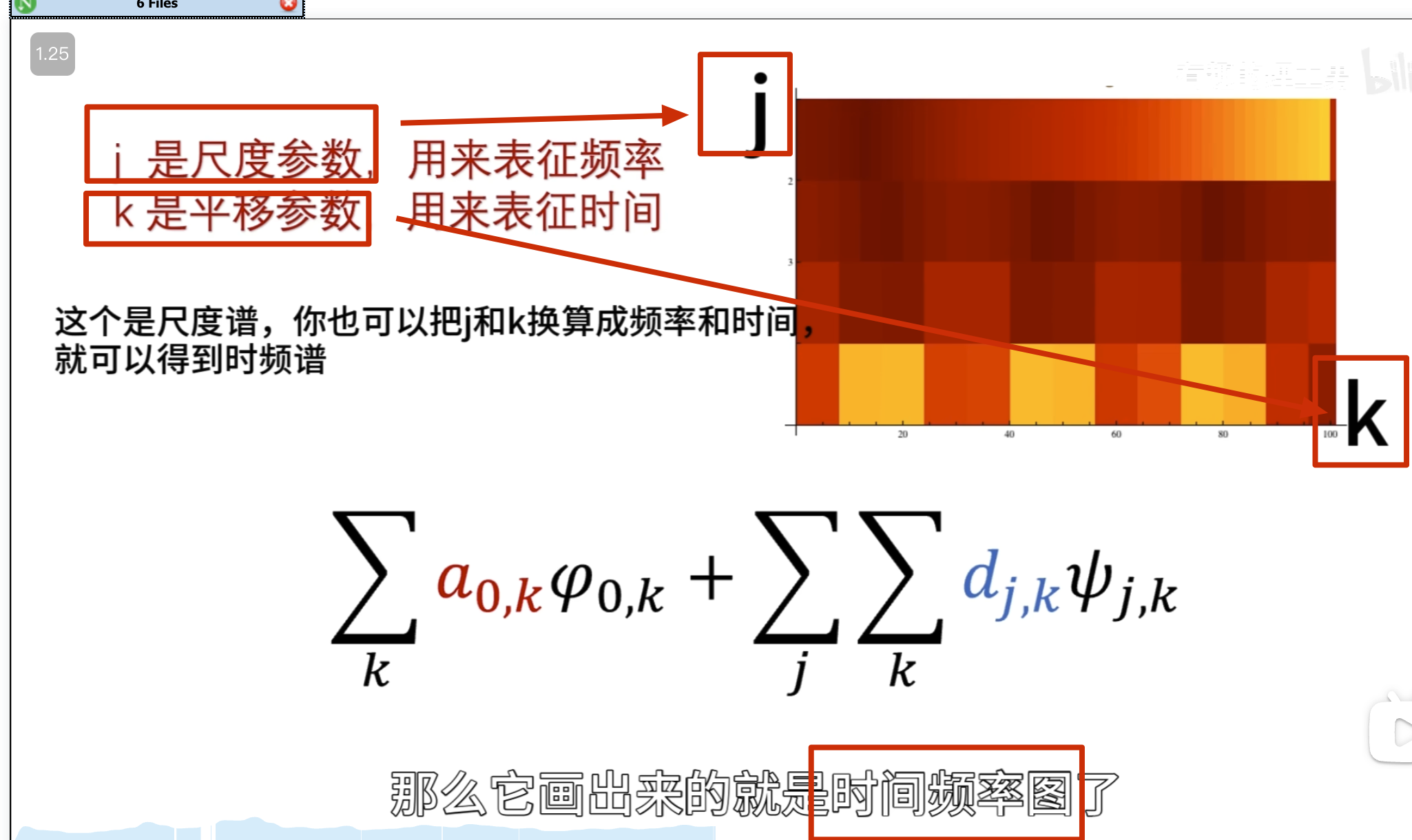
还有个问题,观察者的高低频怎么控制?——增加 a 尺度因子,a 越小表示频率越高
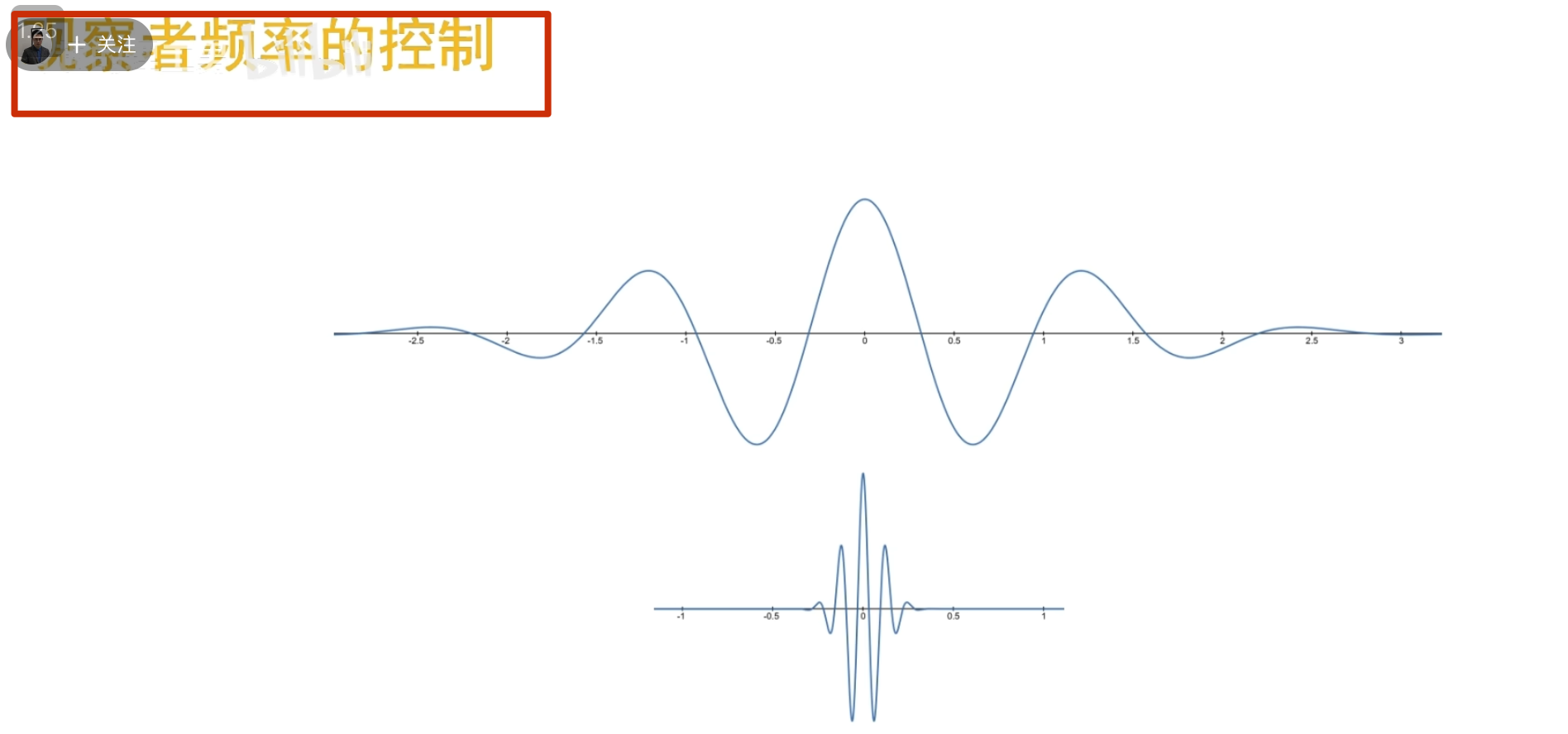
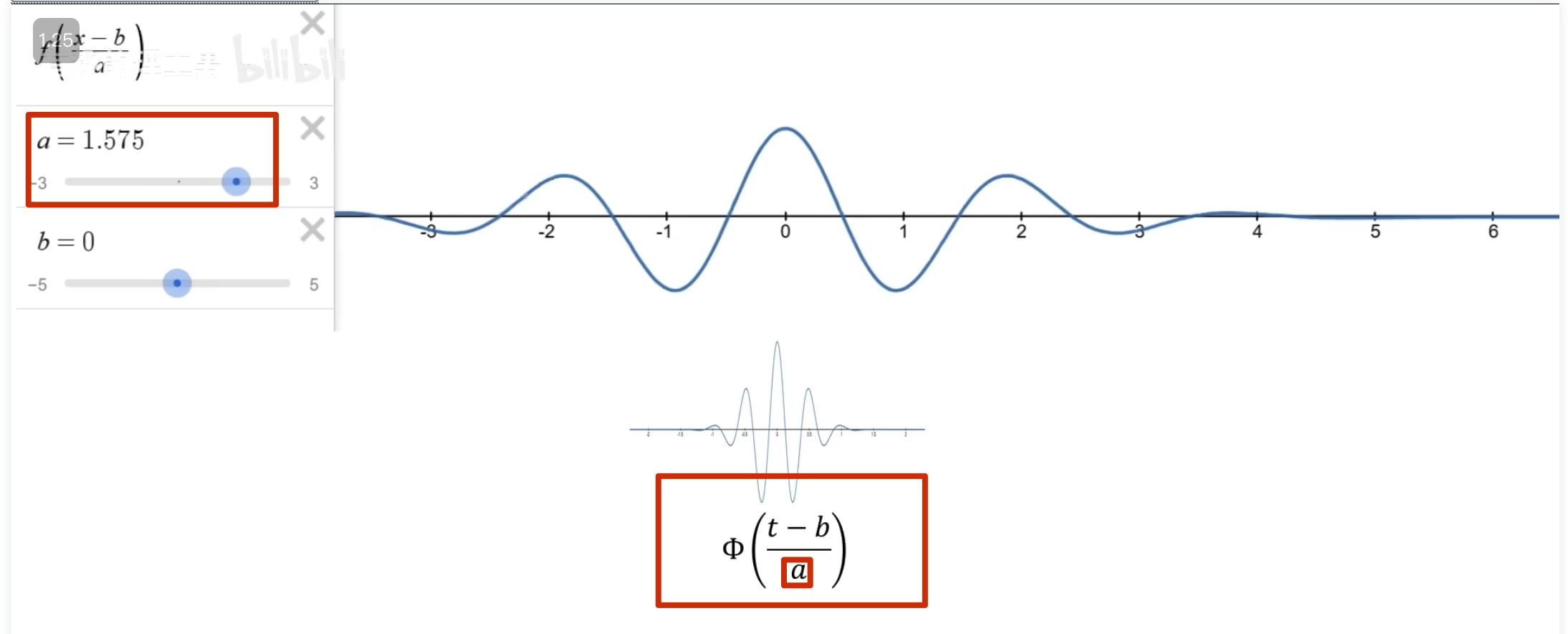
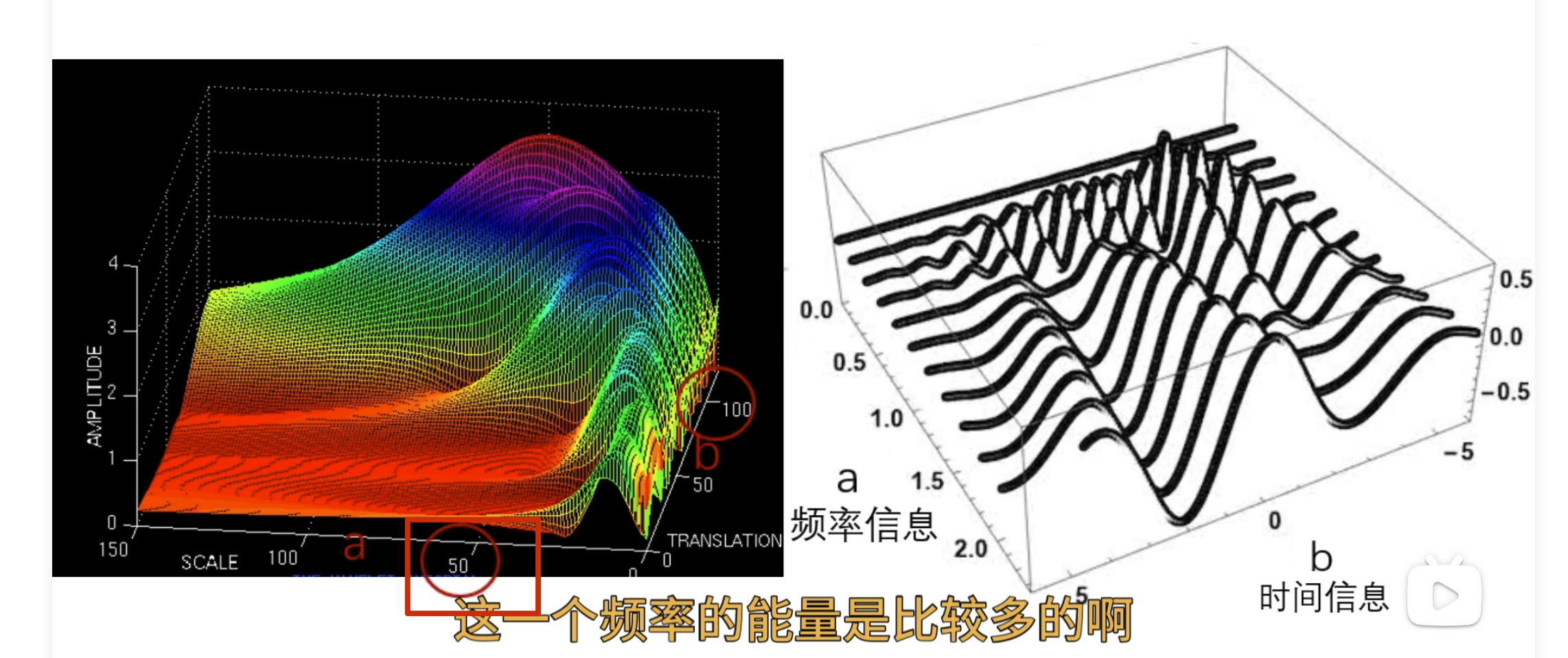
左边是目标函数,右边记录观察结果 ,a 越小表示频率越高
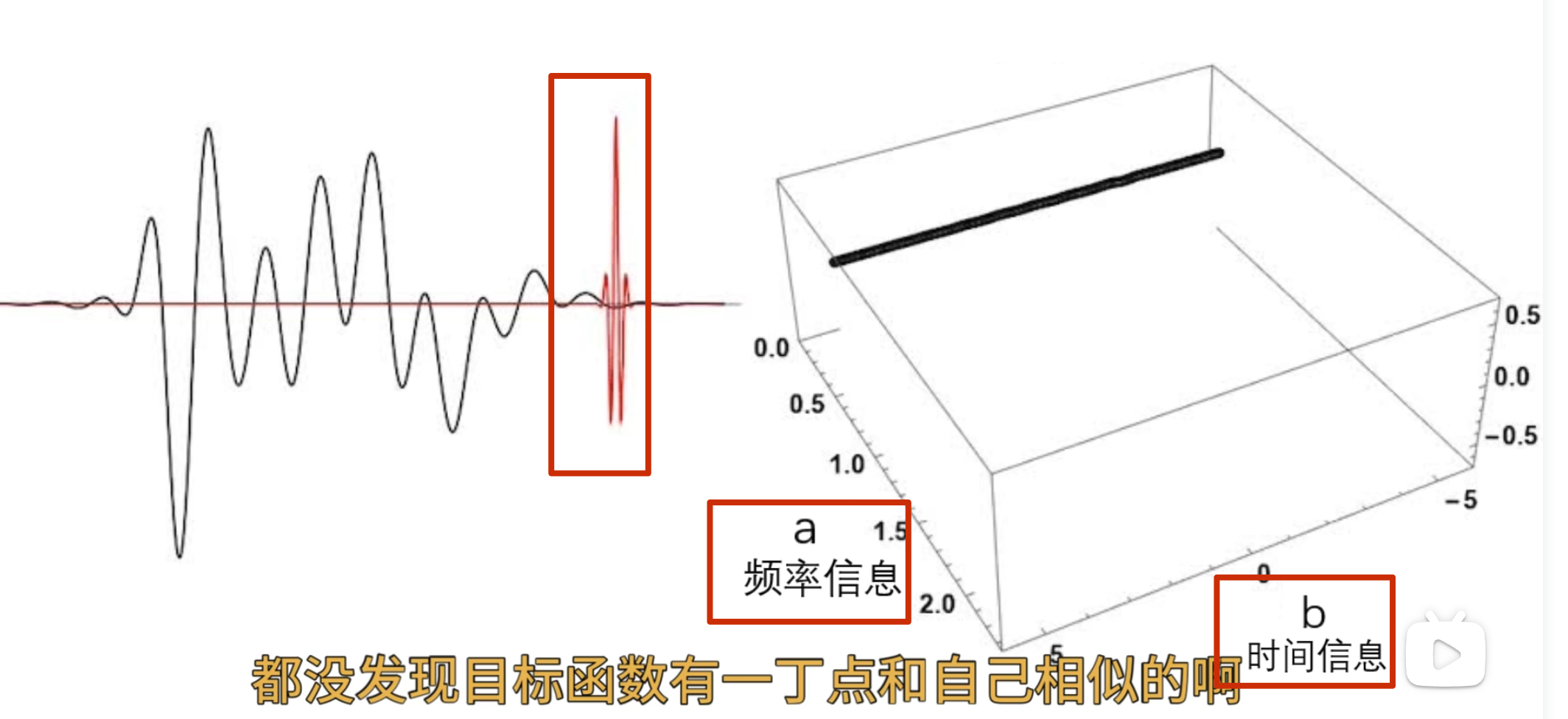
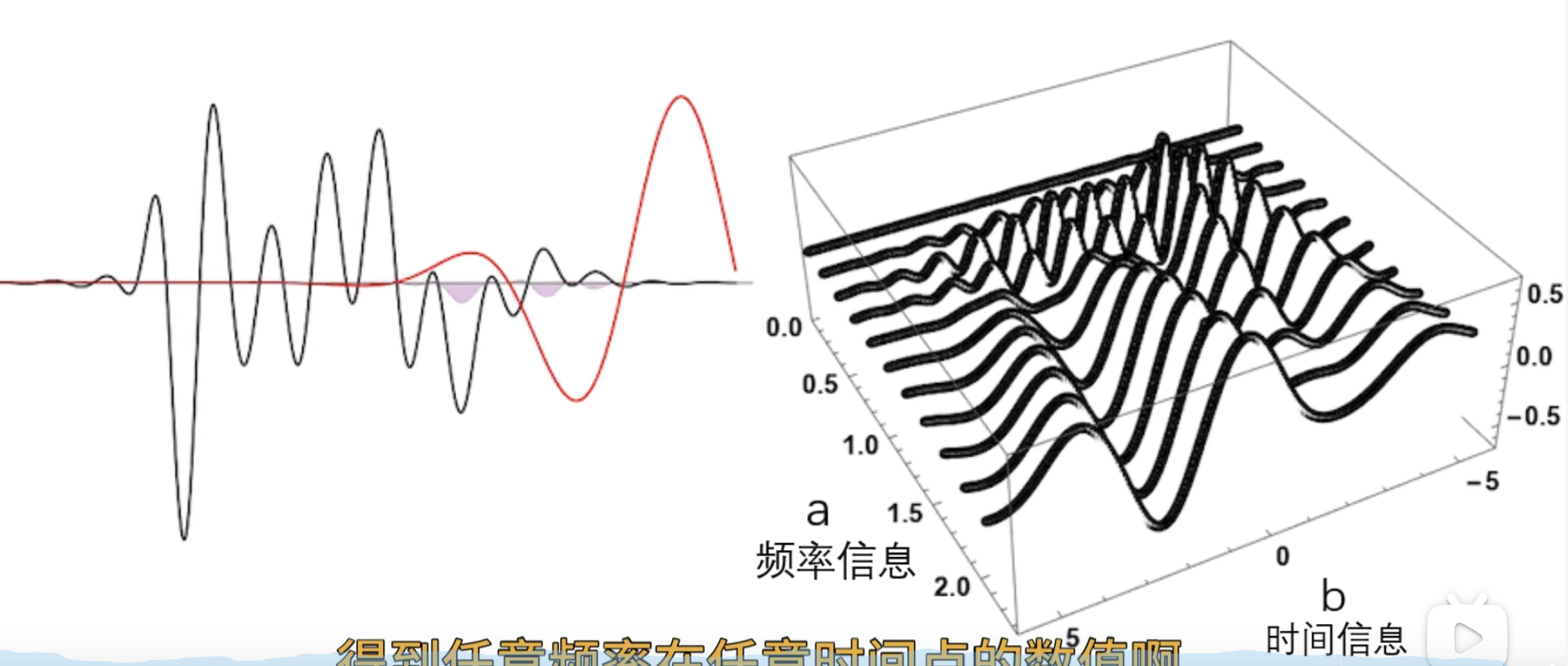
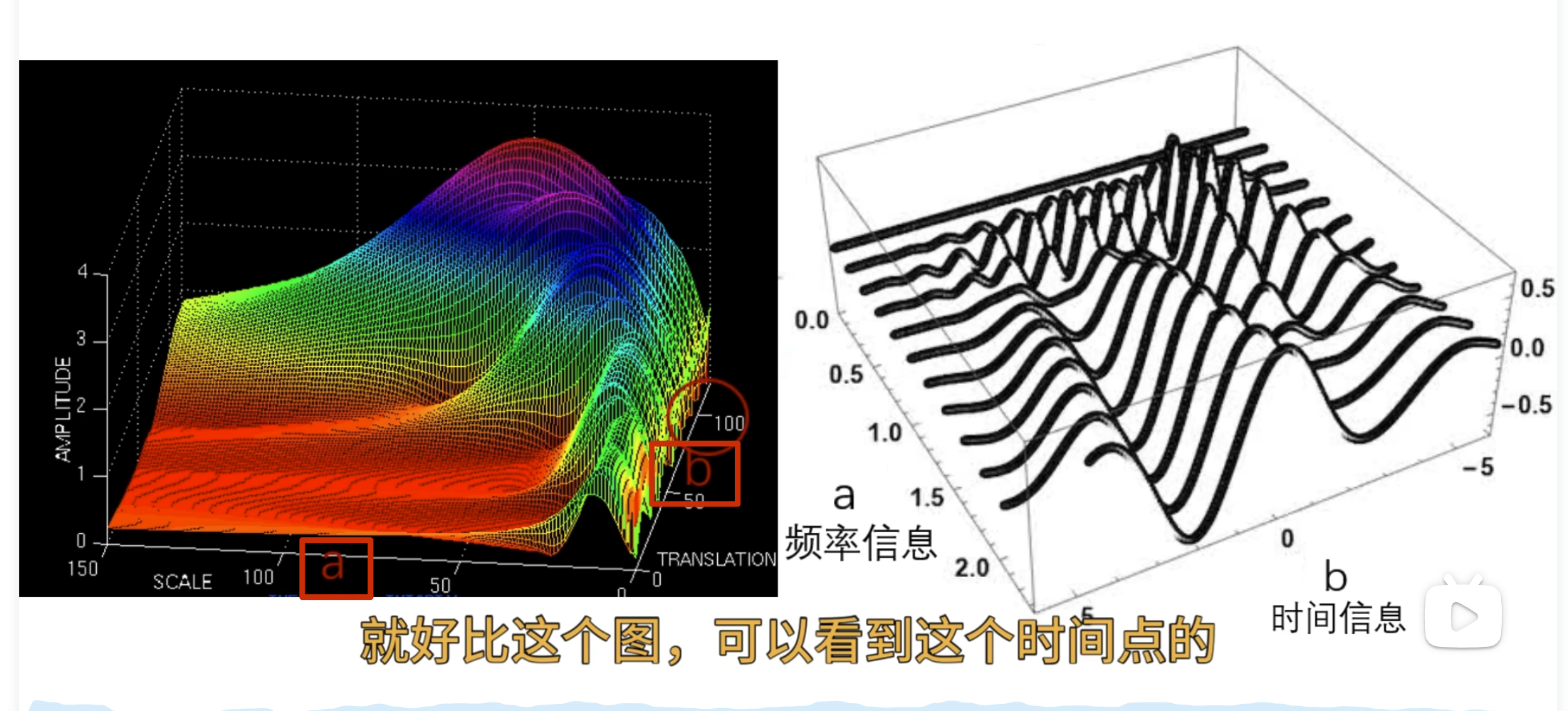
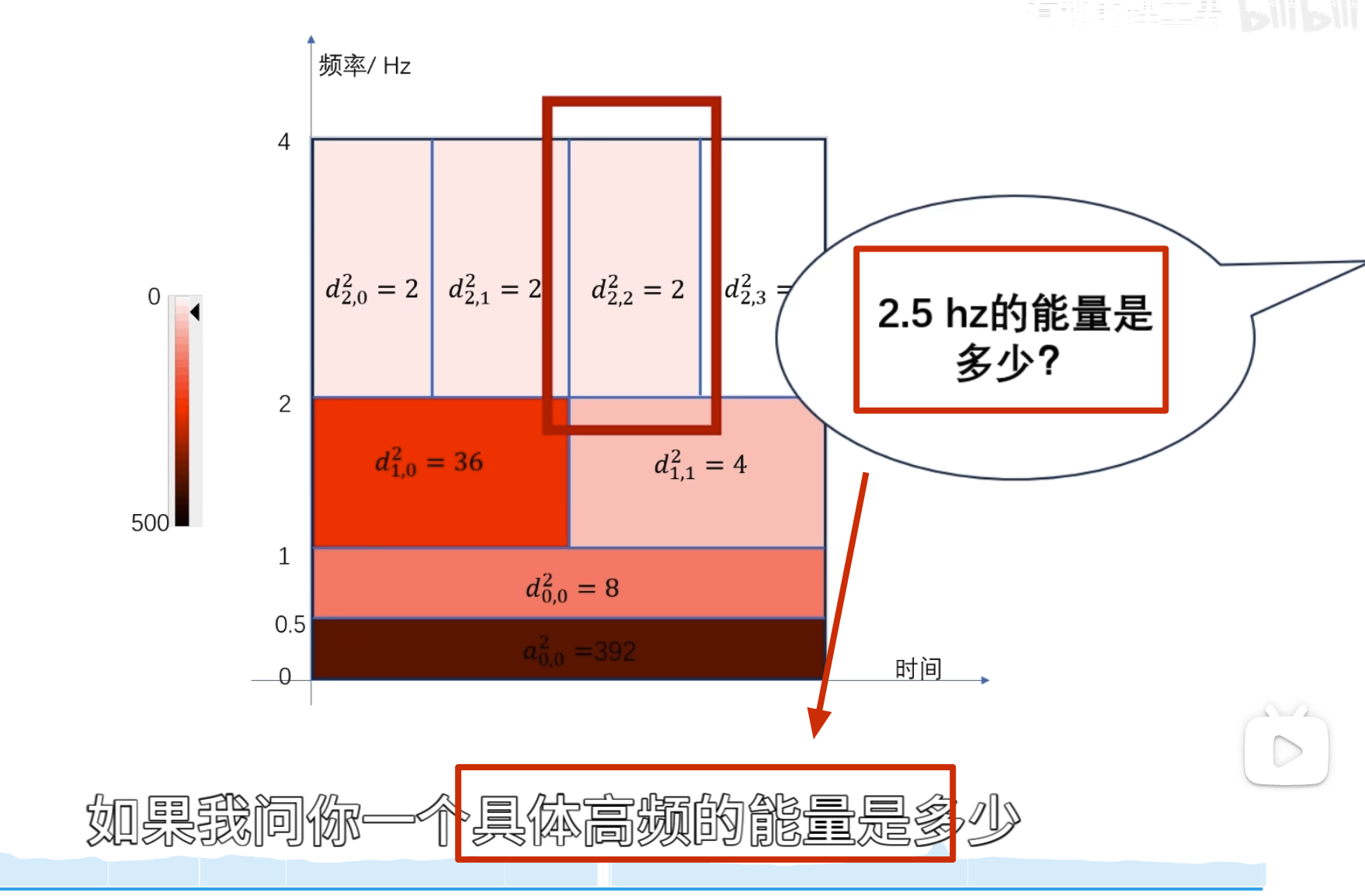
可以看到 50 这个频率的能量比较多

这些一系列在时间轴上做了局域化的观察者就叫小波

小波函数其实是一个非常庞大的家族,根据应閛场景和所䴉的特性不同,所选的小波也不同
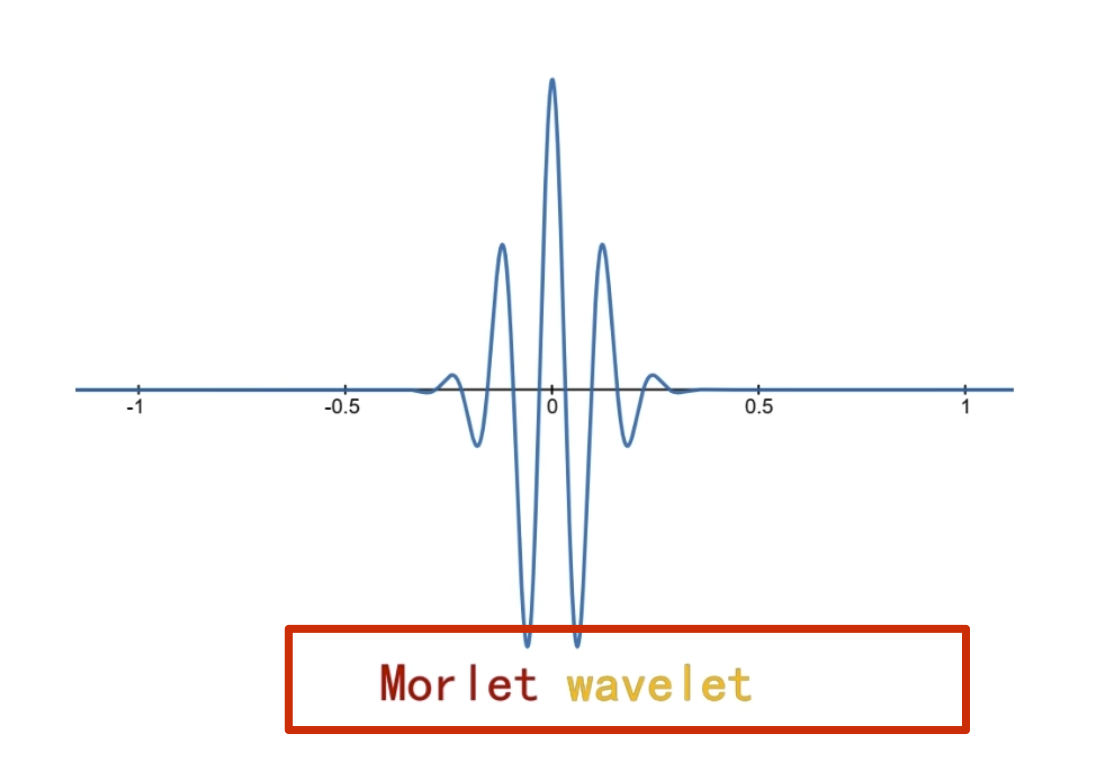
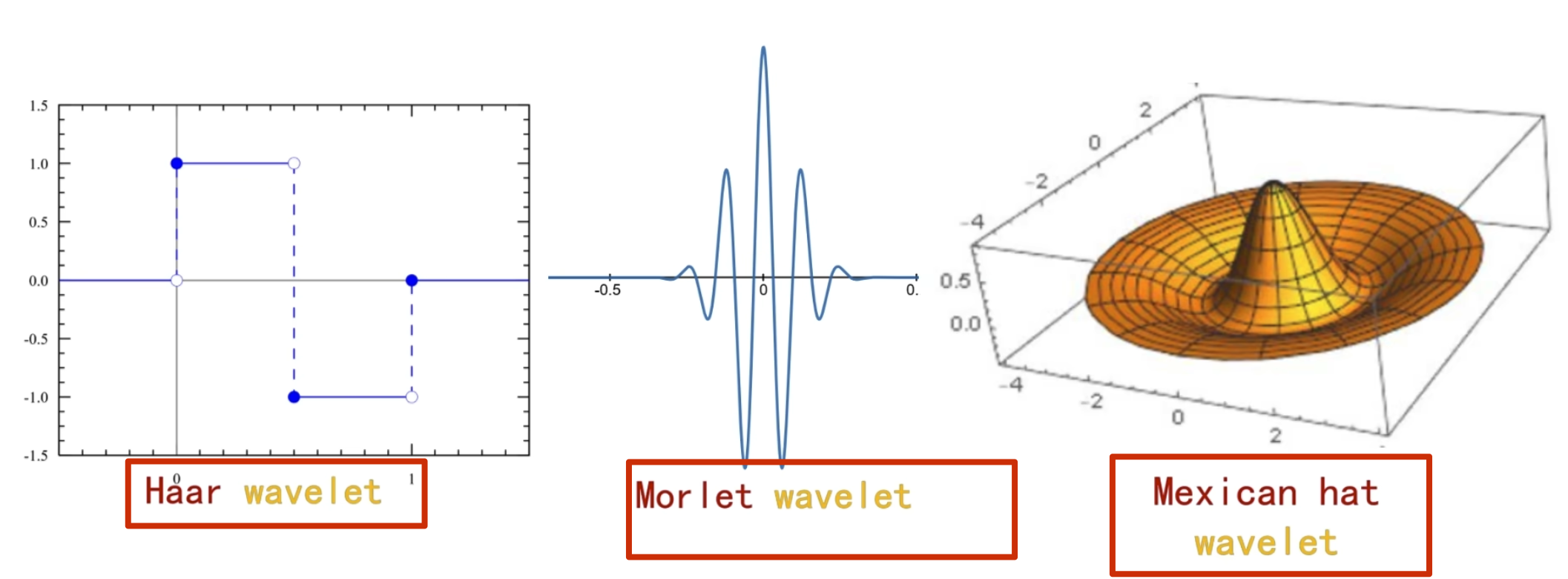
对于小波变换就是把一个信号分解成一系列的小波,这里时候,也许就会问,小波变换的小波是什么啊,定义中就是告诉我们小波,因为这个小波实在是太多,一个是种类多,还有就是同一种小波还可以尺度变换,但是小波在整个时间范围的幅度*均值是0,具有有限的持续时间和突变的频率和振幅,可以是不规则,也可以是不对称,很明显正弦波就不是小波,什么的是呢,看下面几个图就是
最终计算相似度的公式如下(因为能量不同,所以还是需要归一化)
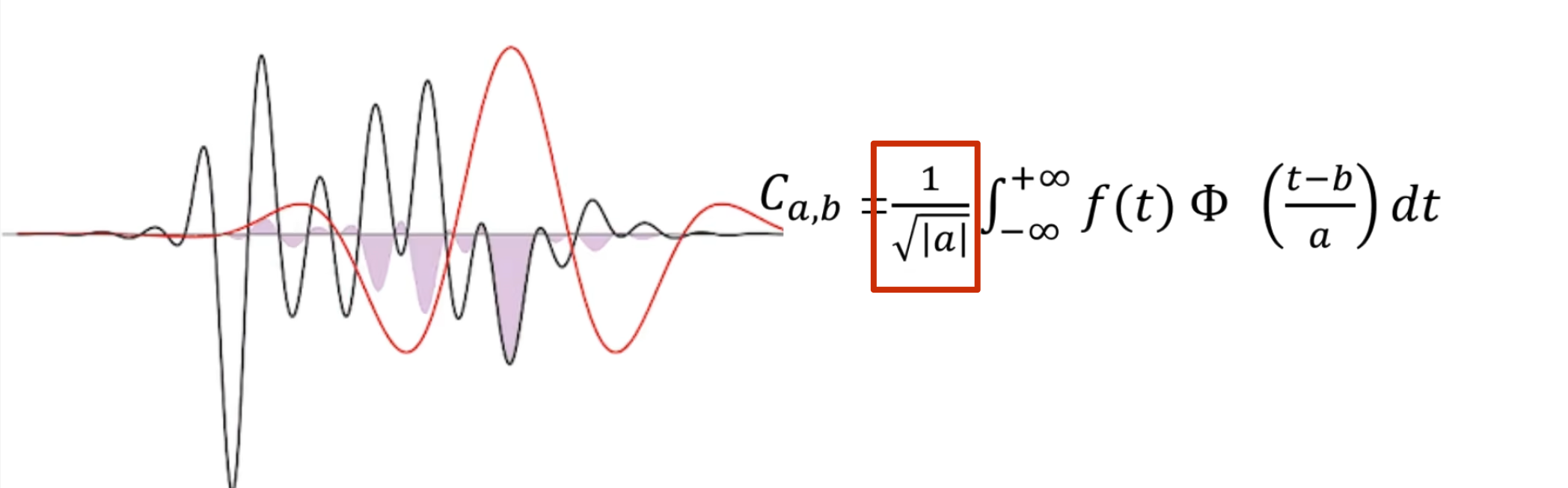
同时上面 演示的还是实函数的小波变换,对于虚函数的小波变换如下
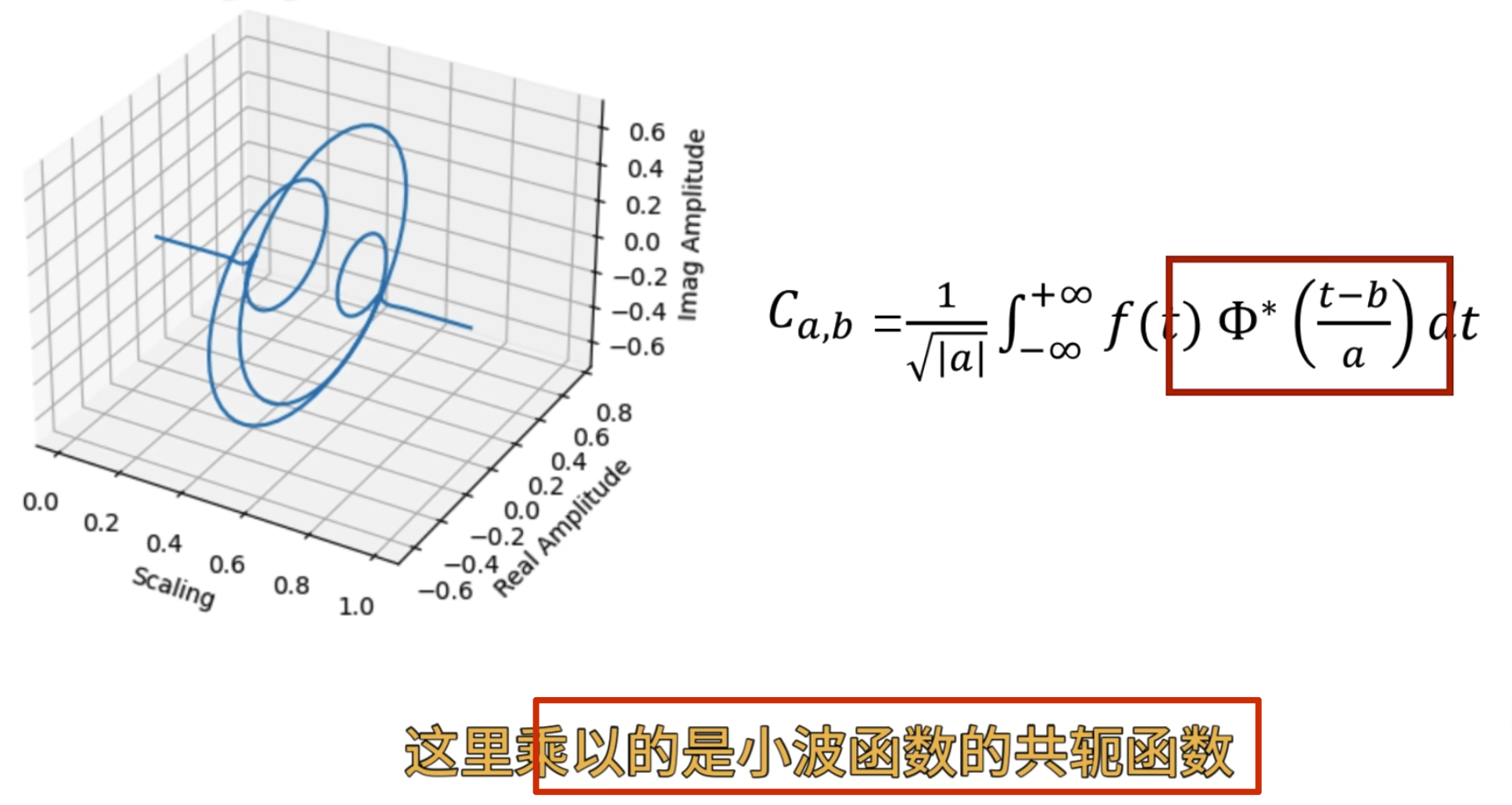
再从另卷积的角度看小波变换:
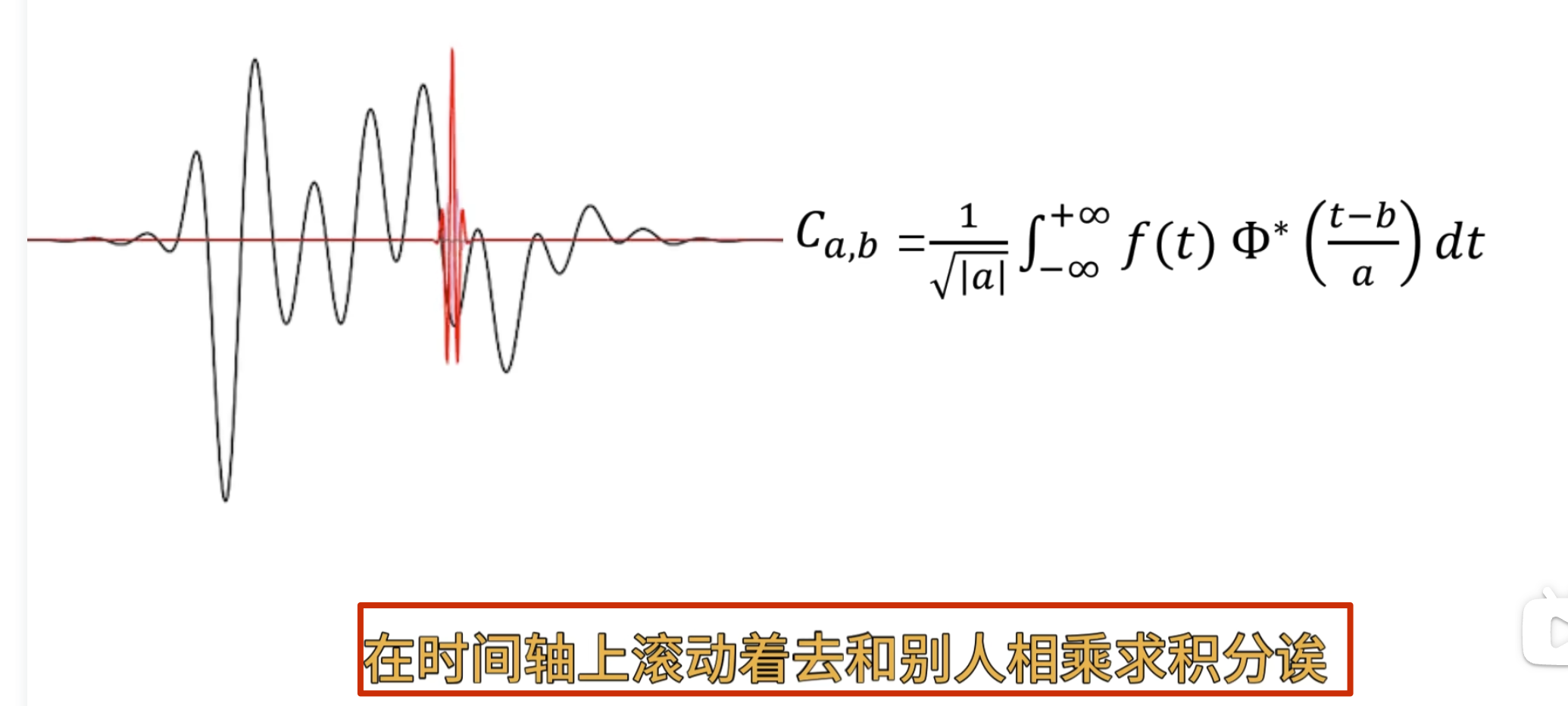


小波变换应用——重建目标函数
上面只是观察了一个序列的相似程度,但是有什么用呢? ——将目标函数给还原回来
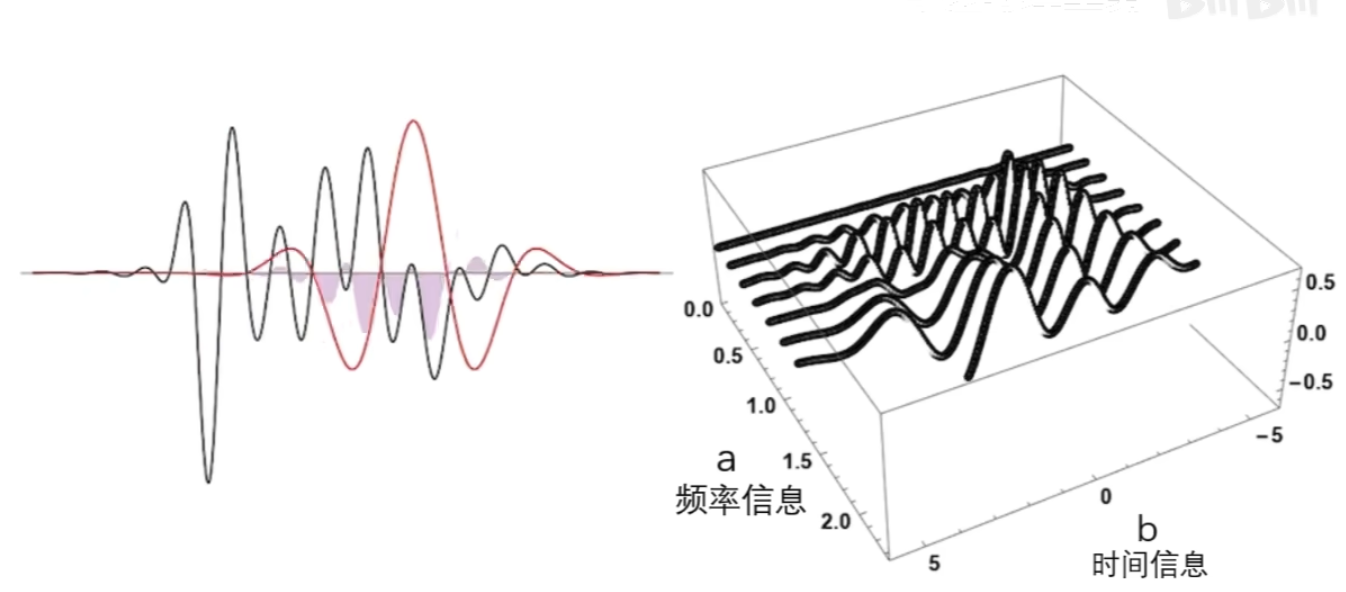
上面观察者的使命还没有完成,因为我们不会无缘无故地观察一个东西的

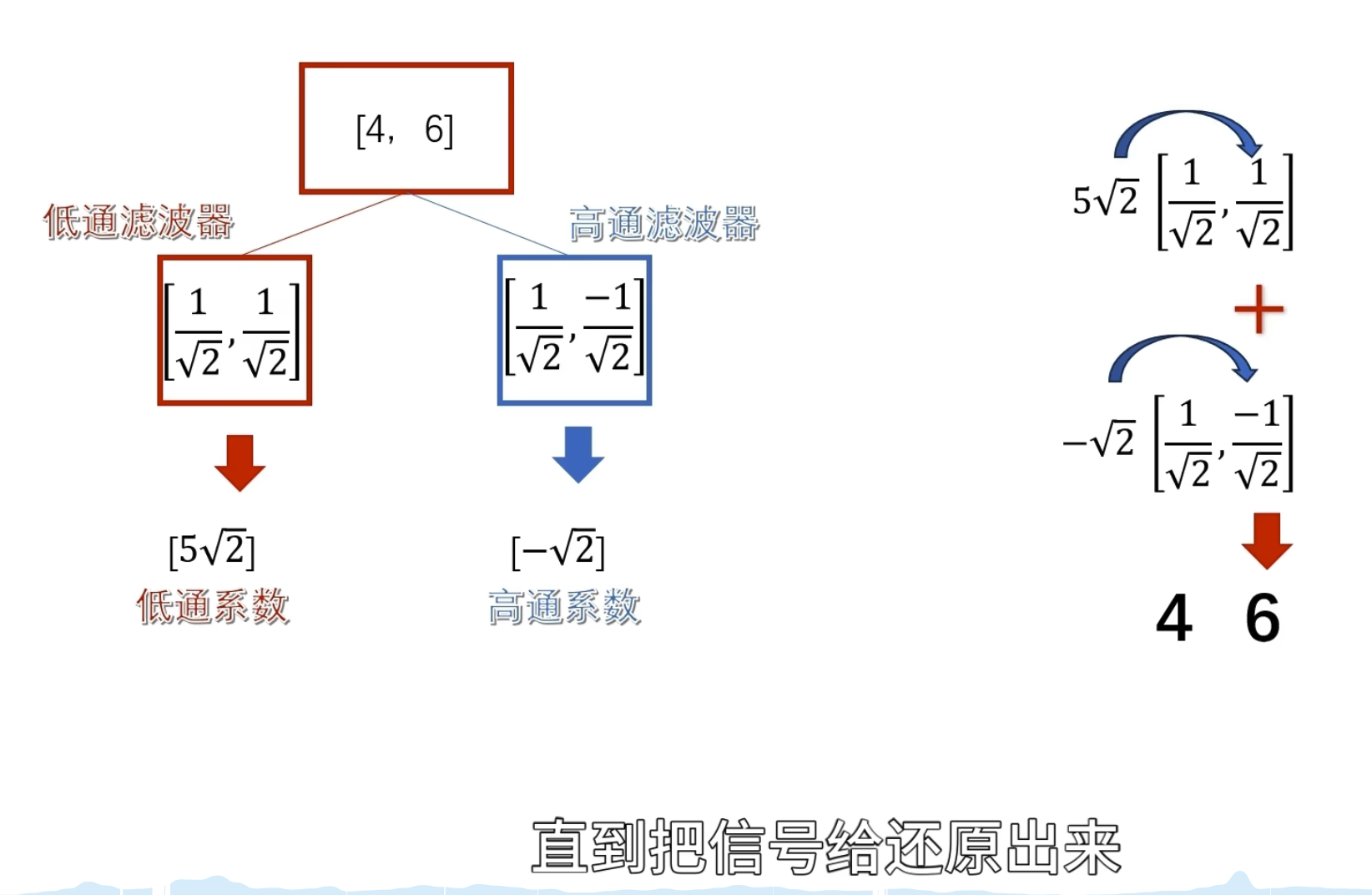
当我们要还原目标的时候,用这些柔数乘以观察者再把他们给加起来啊,就可以对目标进行完美的复制还原了

这种公式其实是观察者对目标 进行了重构,观察者同时叉是建造者

关键在于可以在重构的时候动手脚,可以把你认为的无用的观察者给抹掉,或者是对某些观察者进行有目的的加强,然后再重构


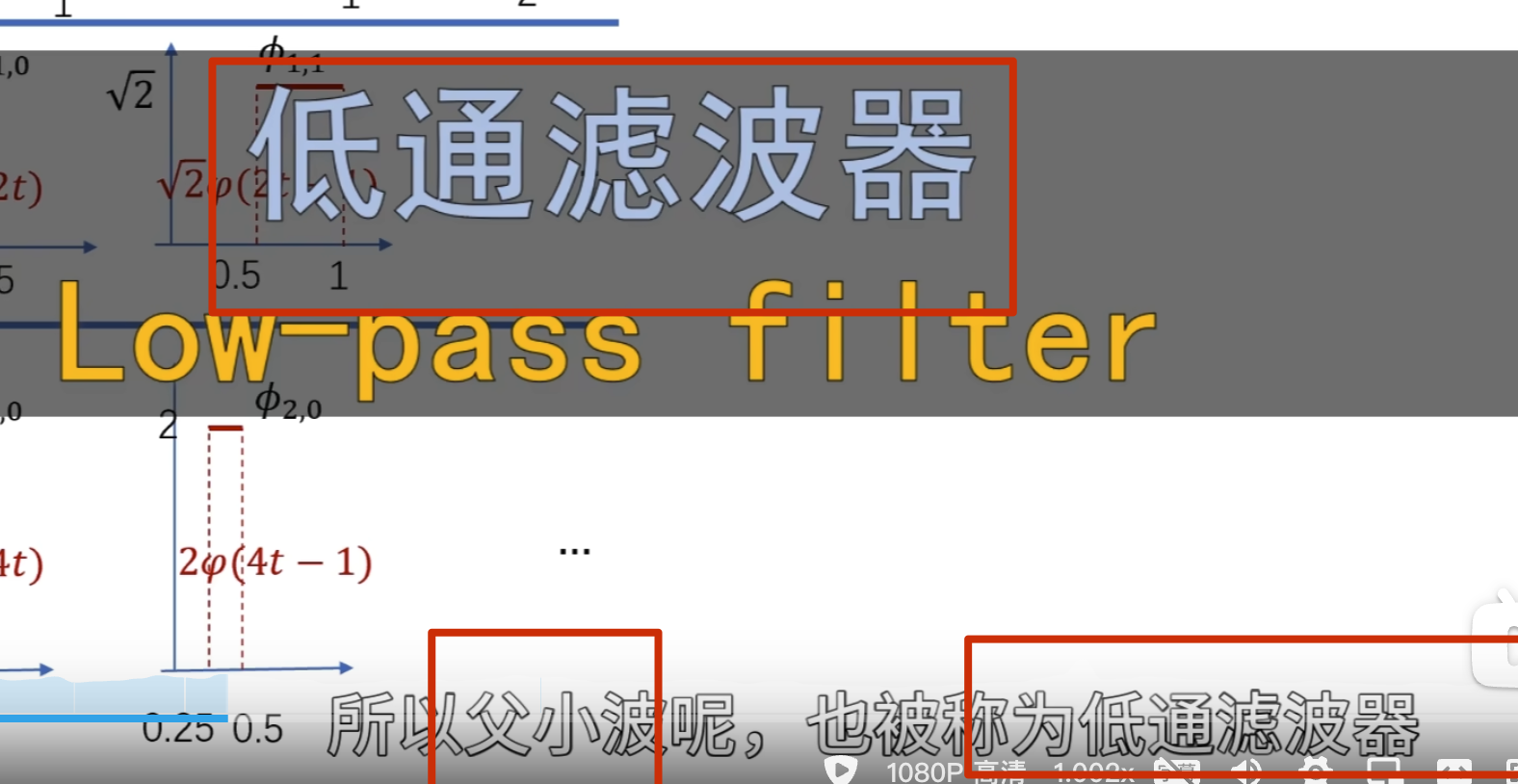
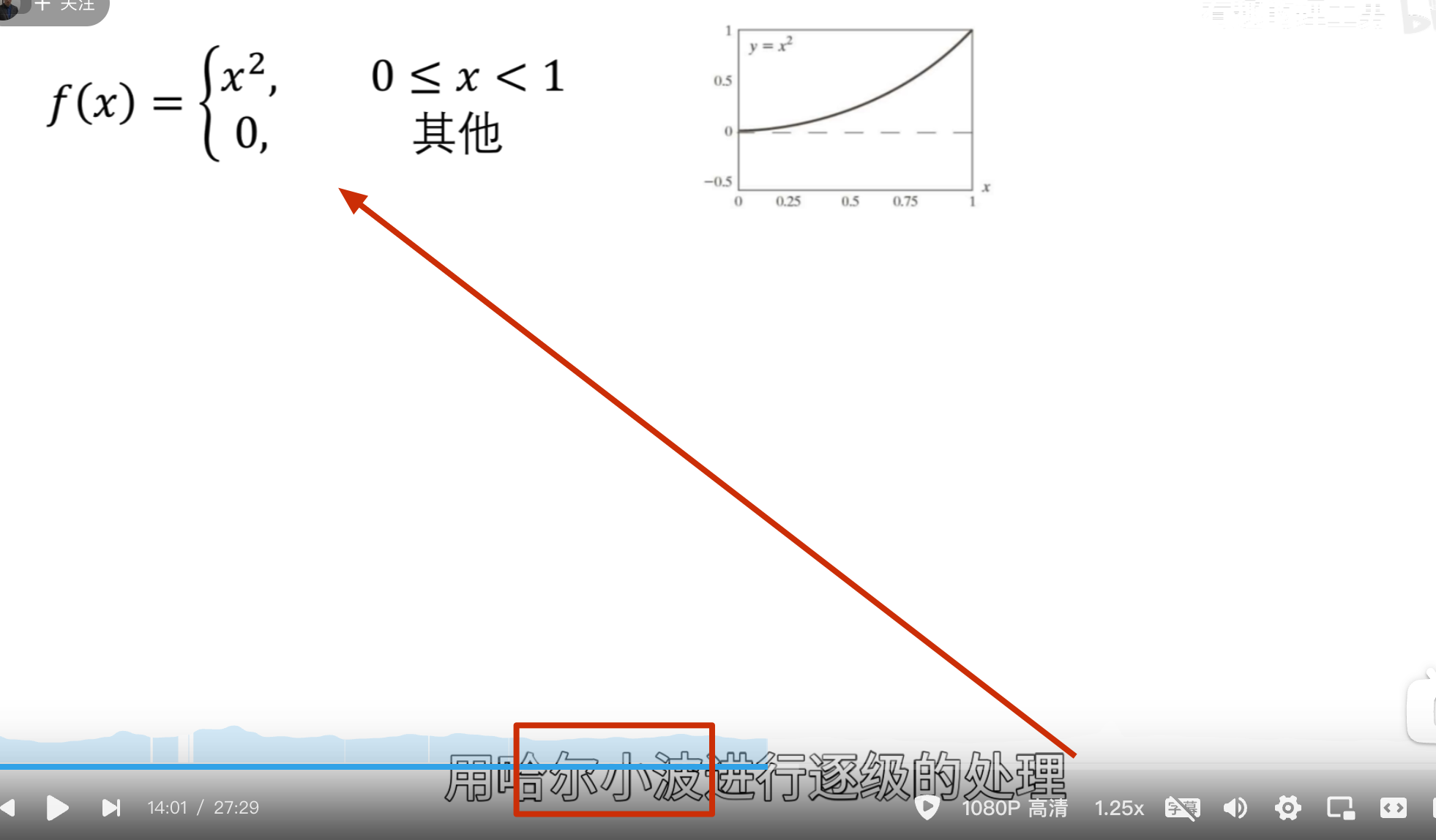
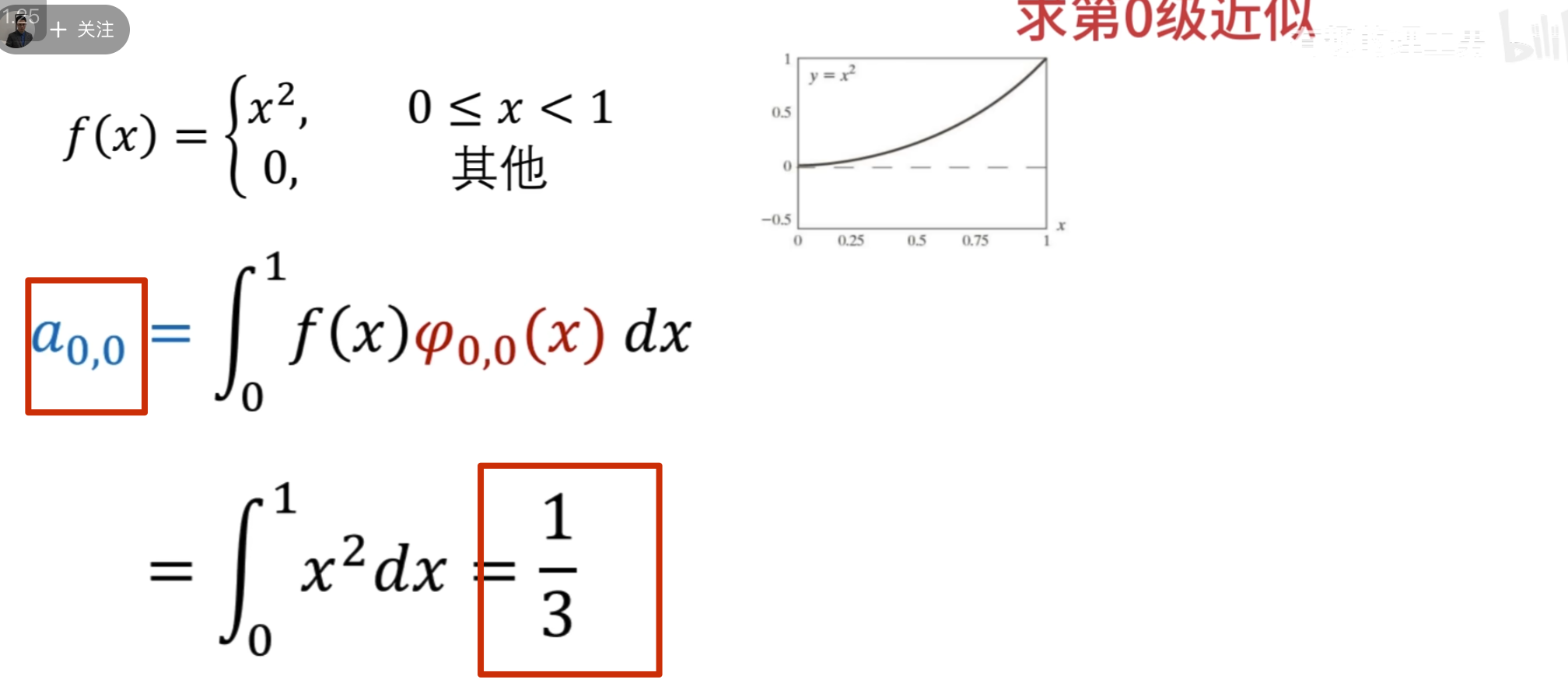
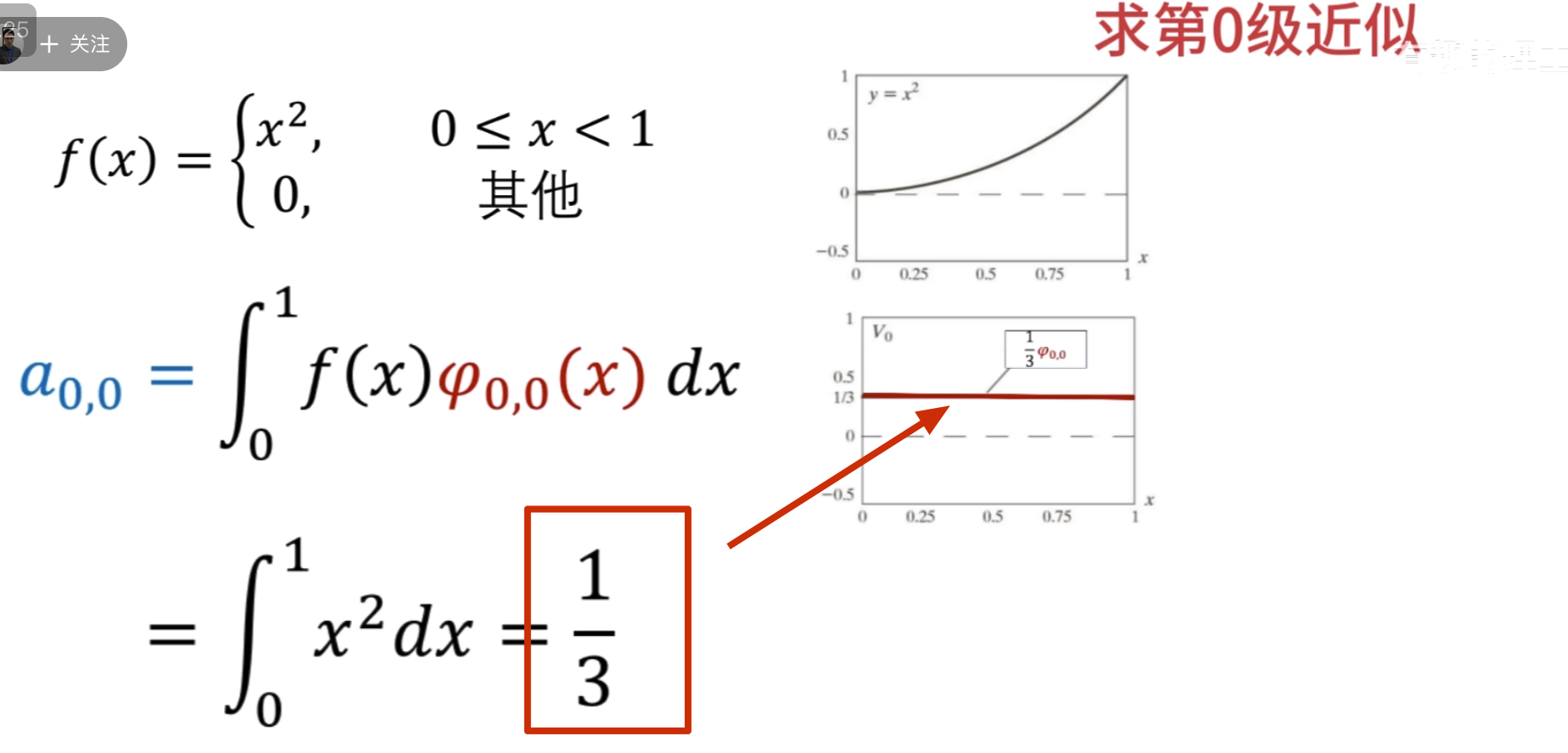
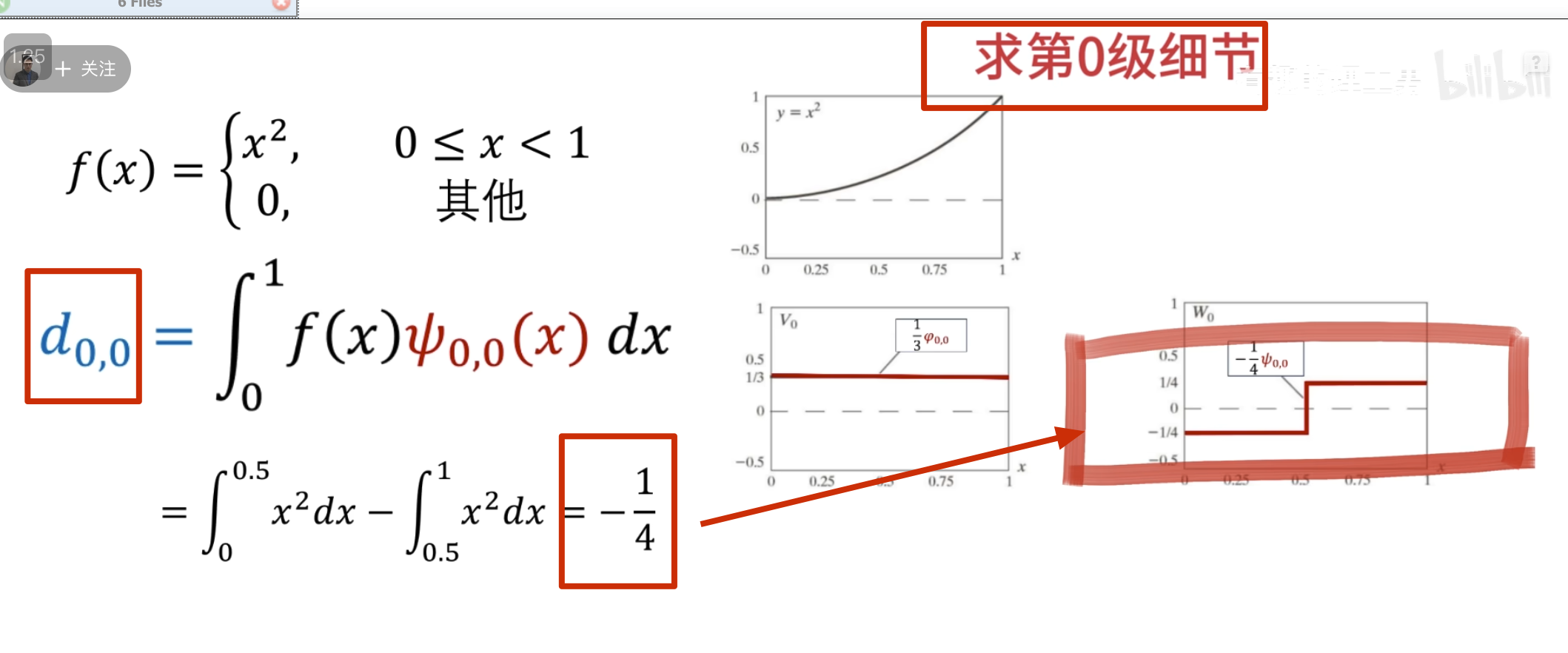
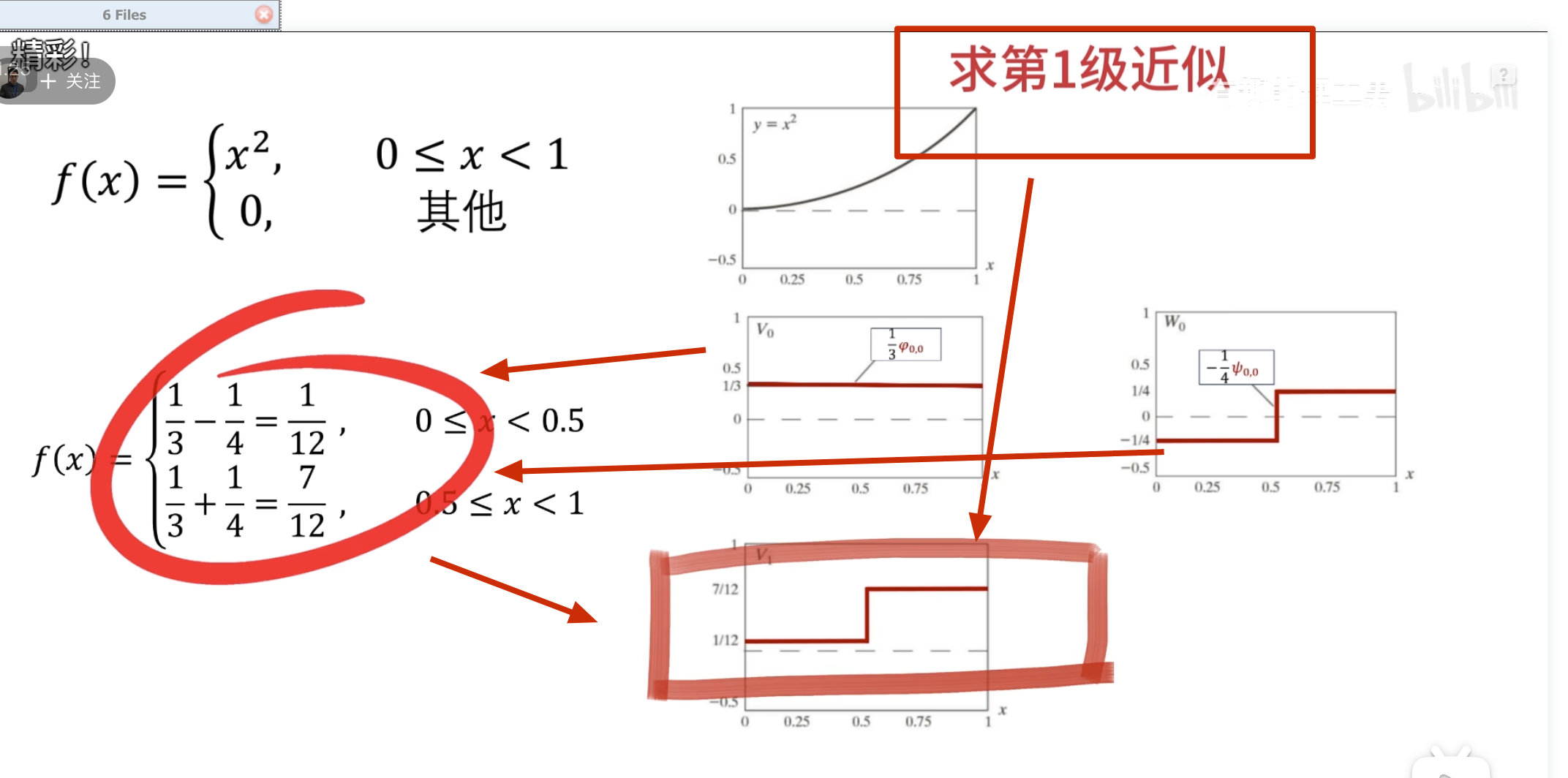
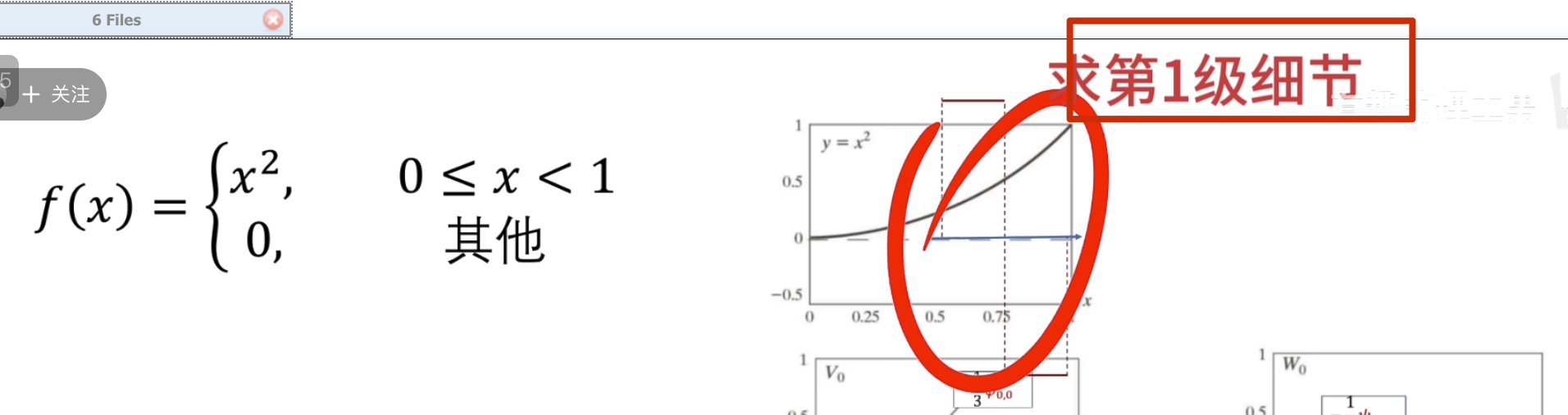
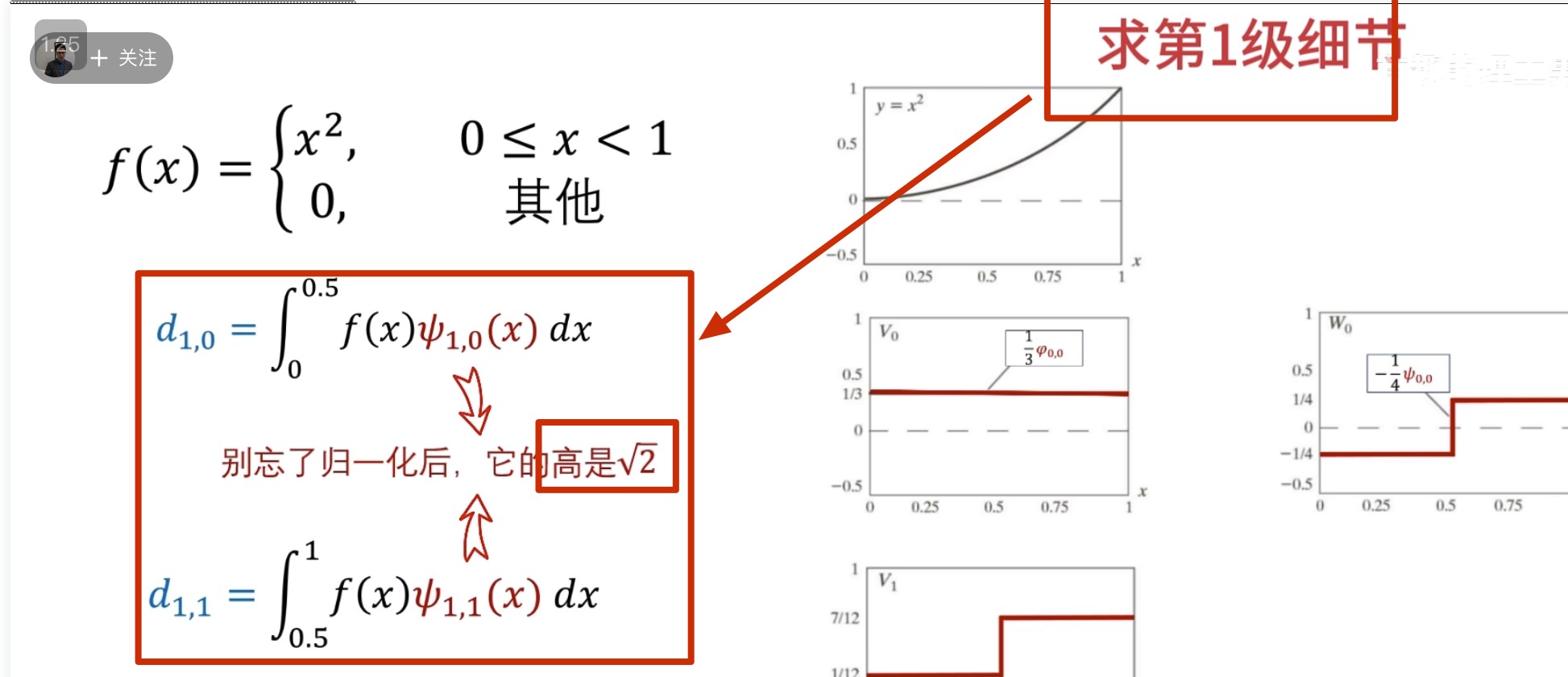
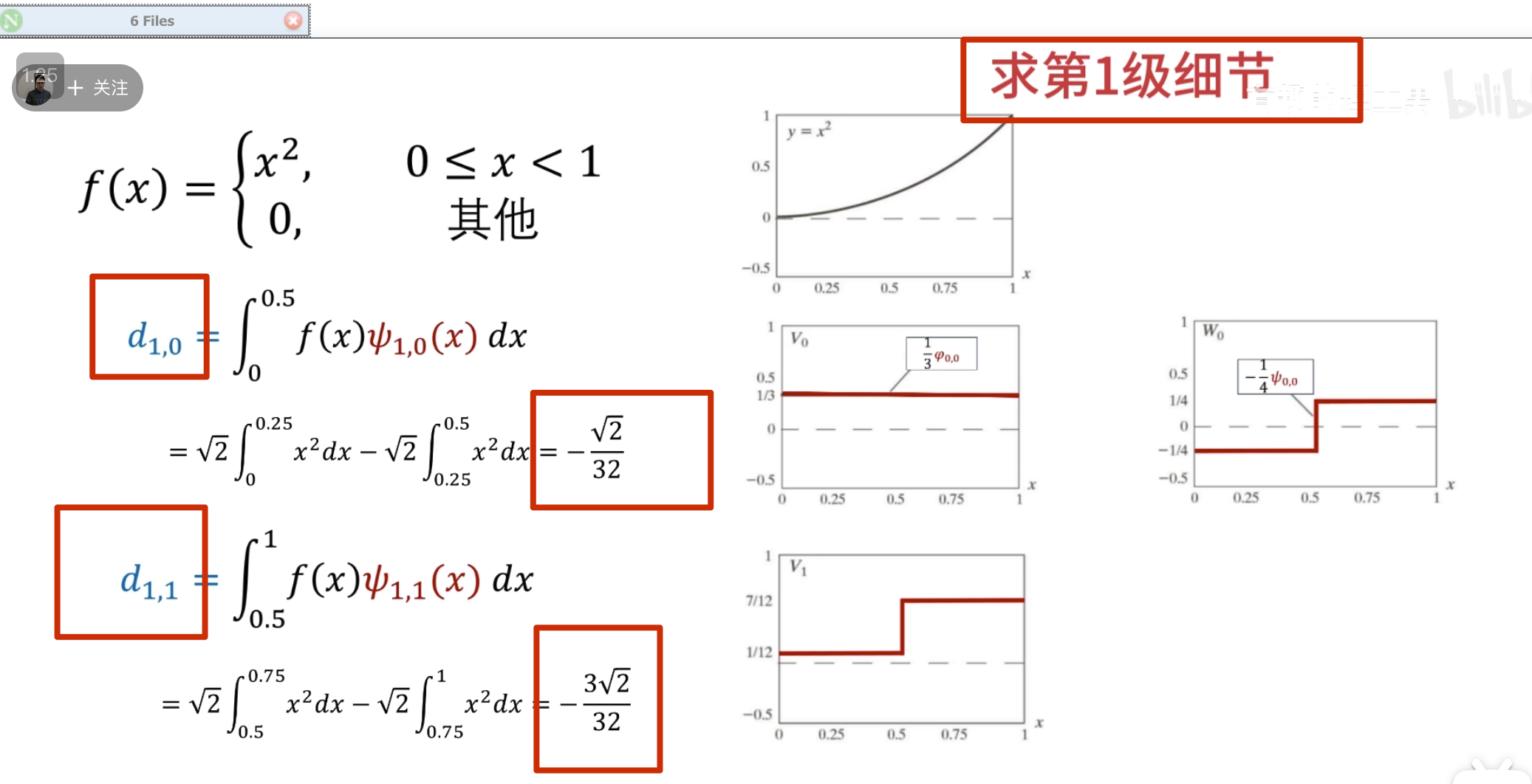
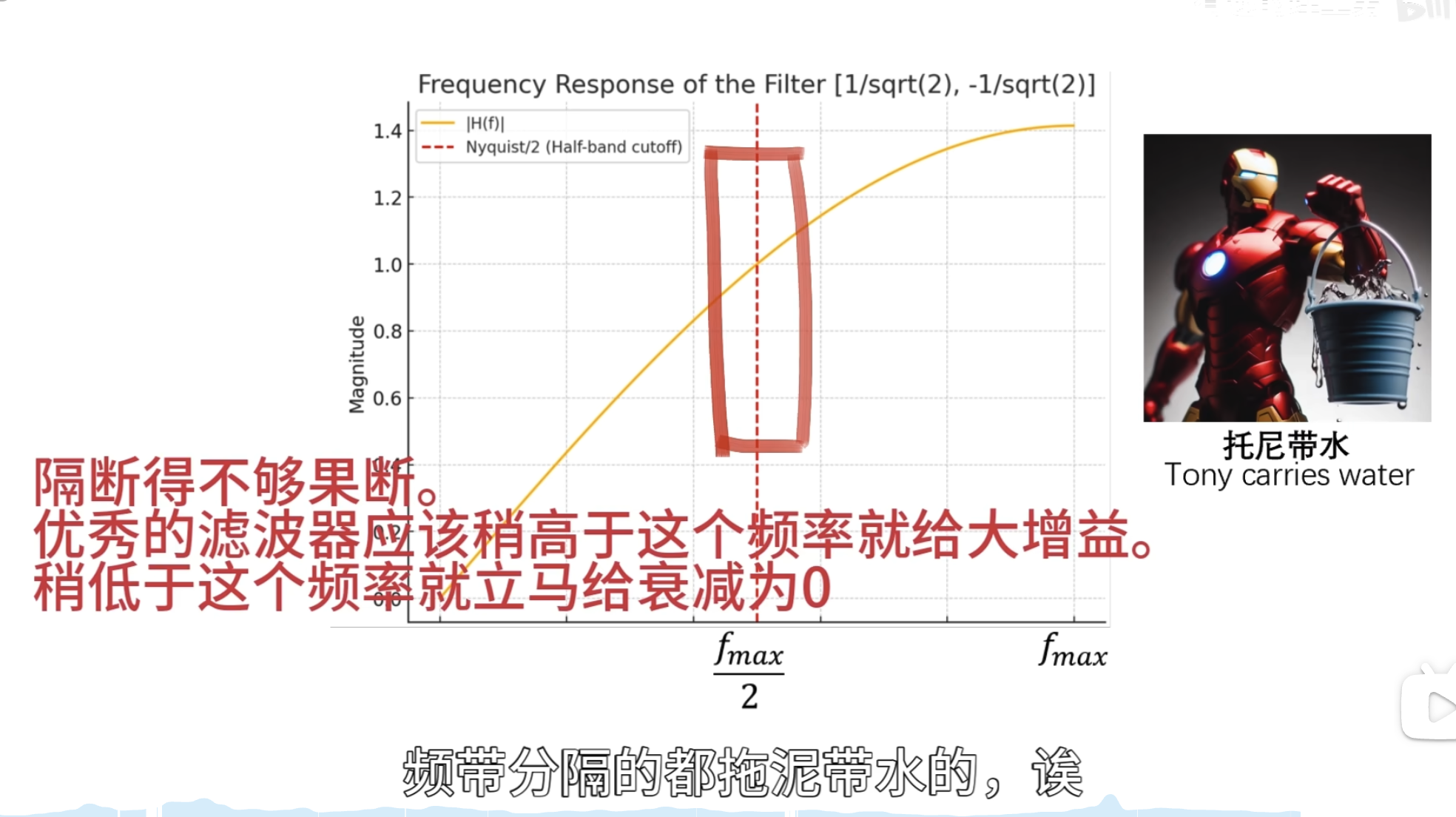
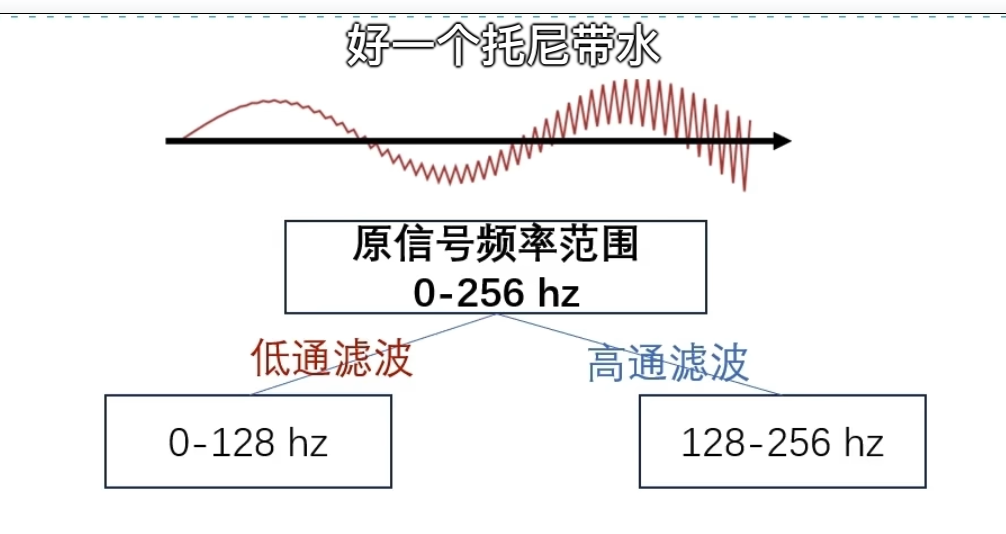
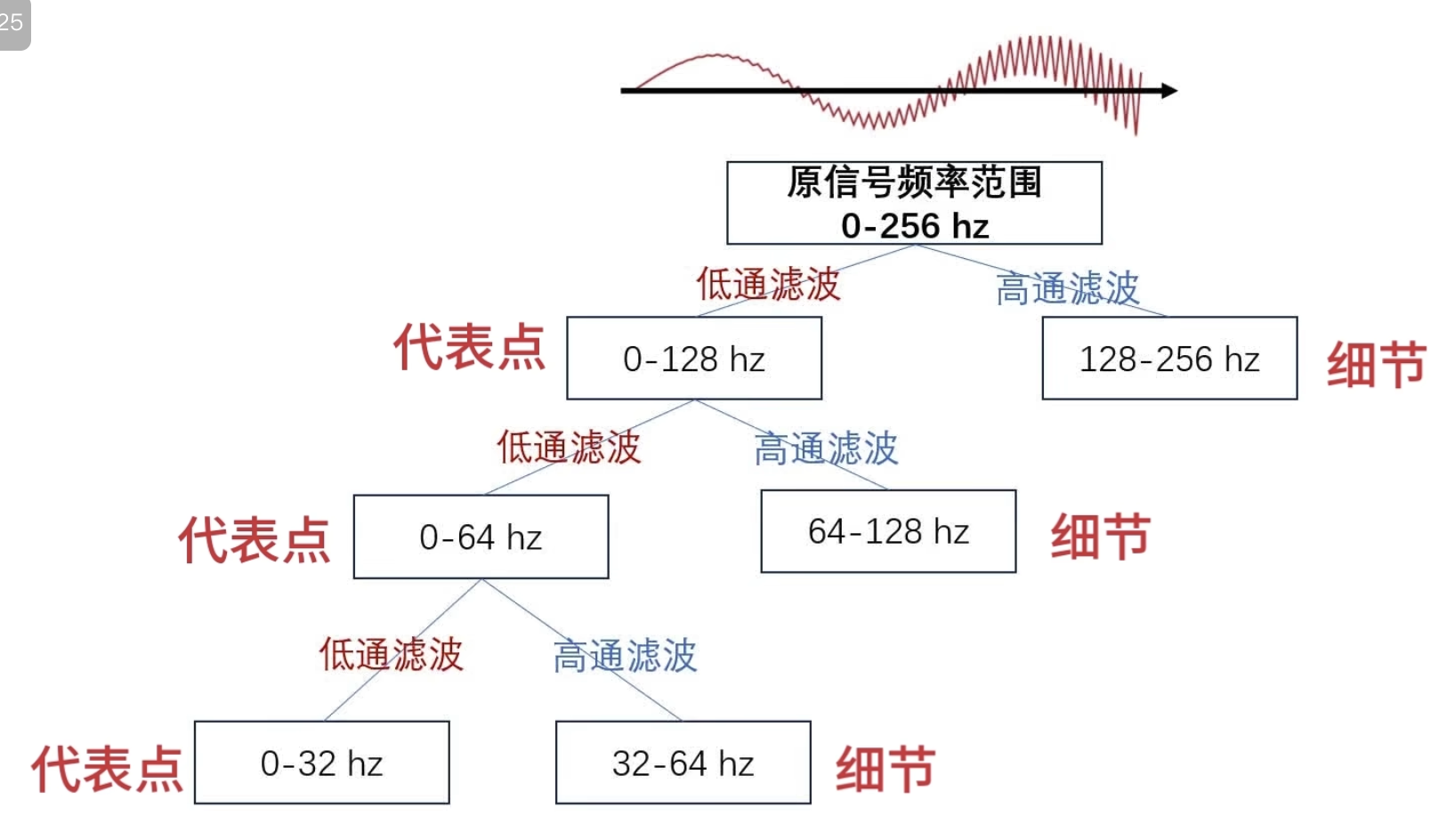
要把下面这条曲线重新绘制出来怎么做?
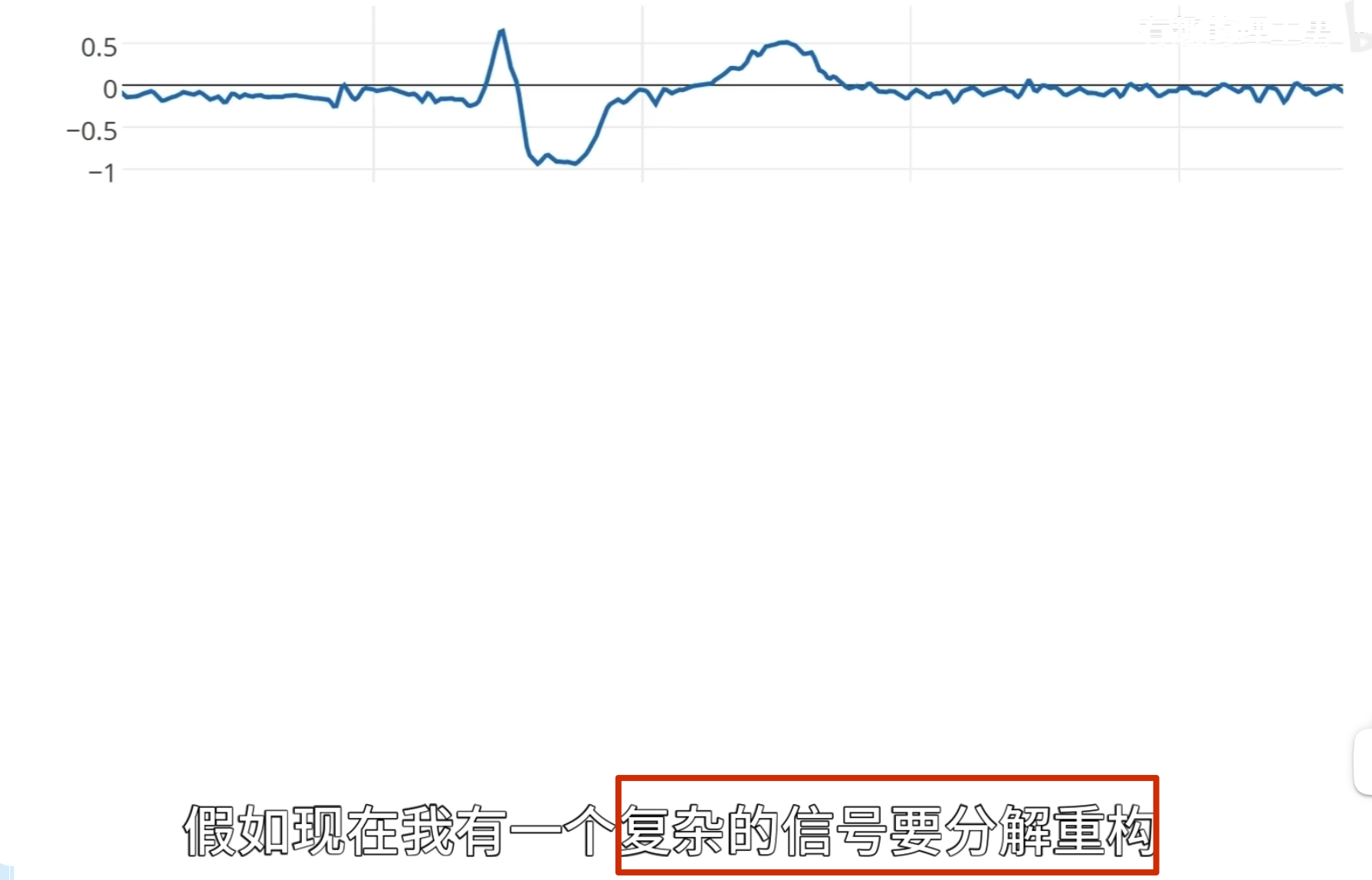
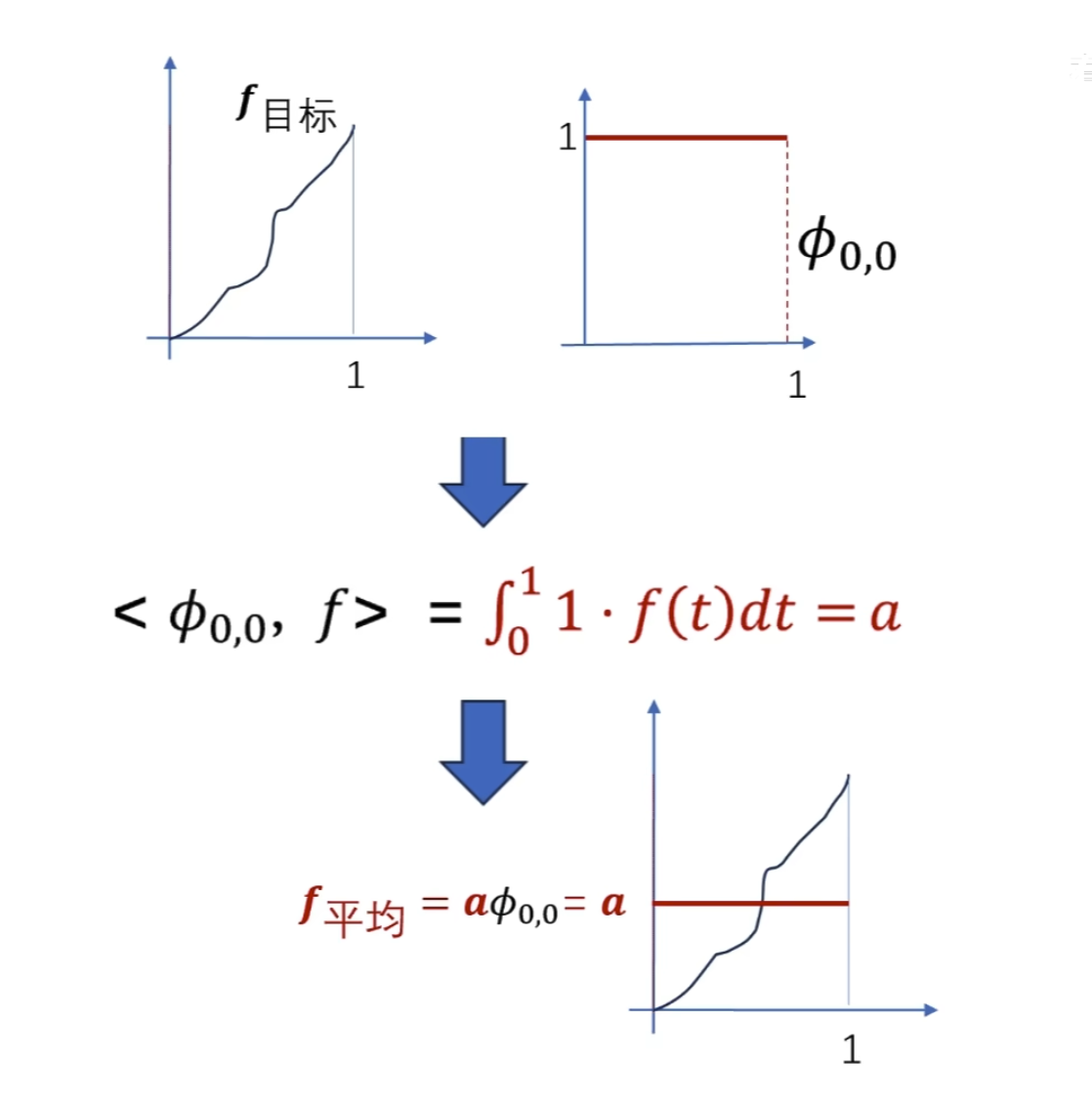
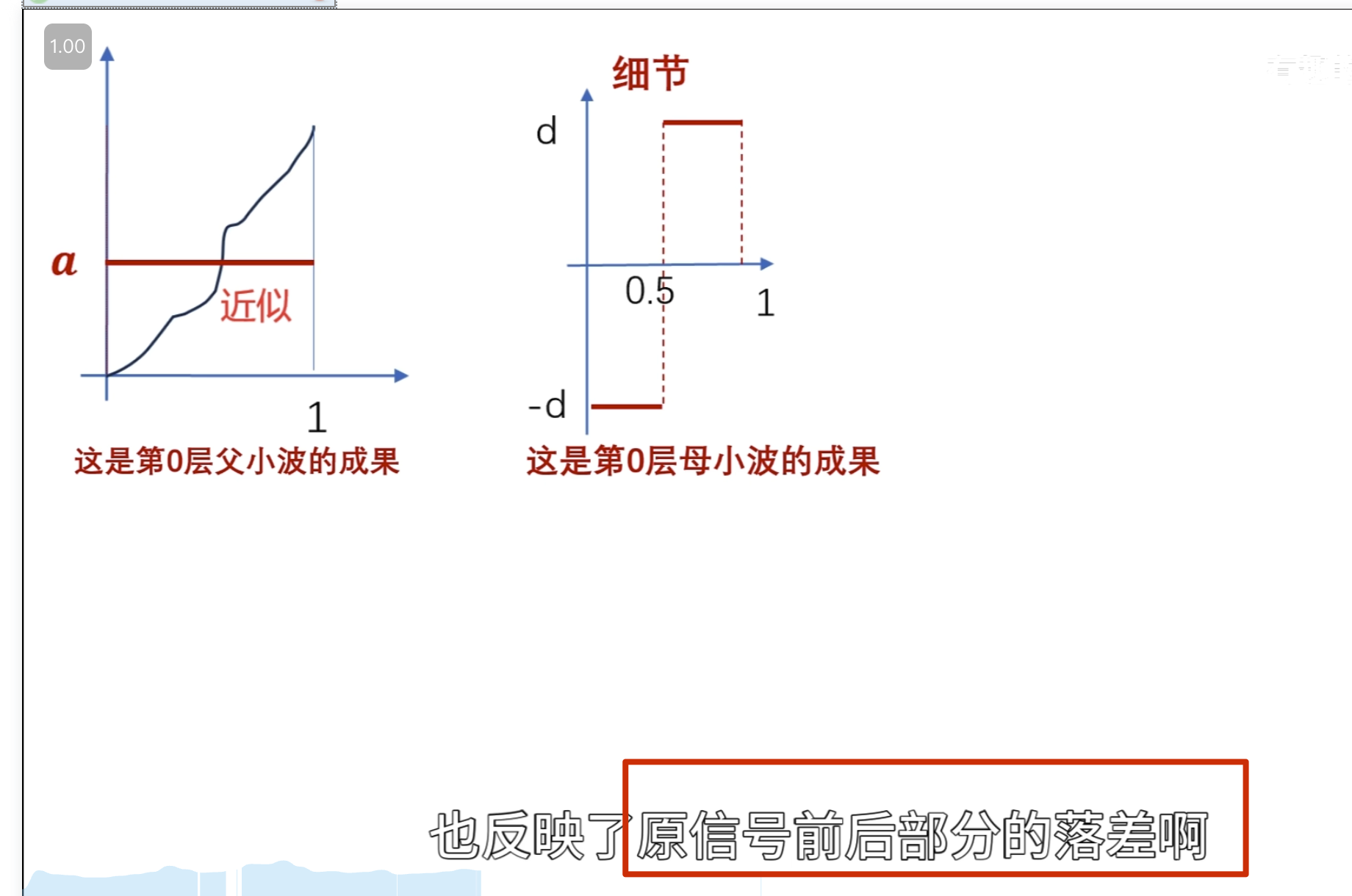
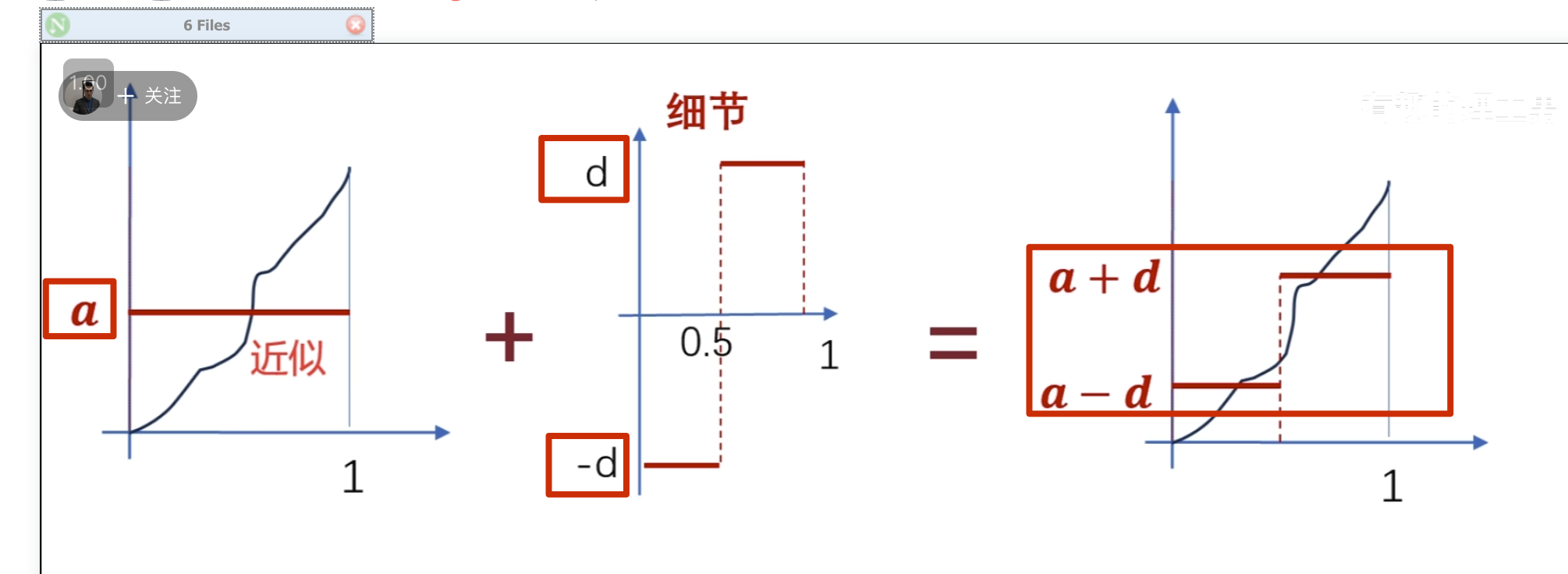
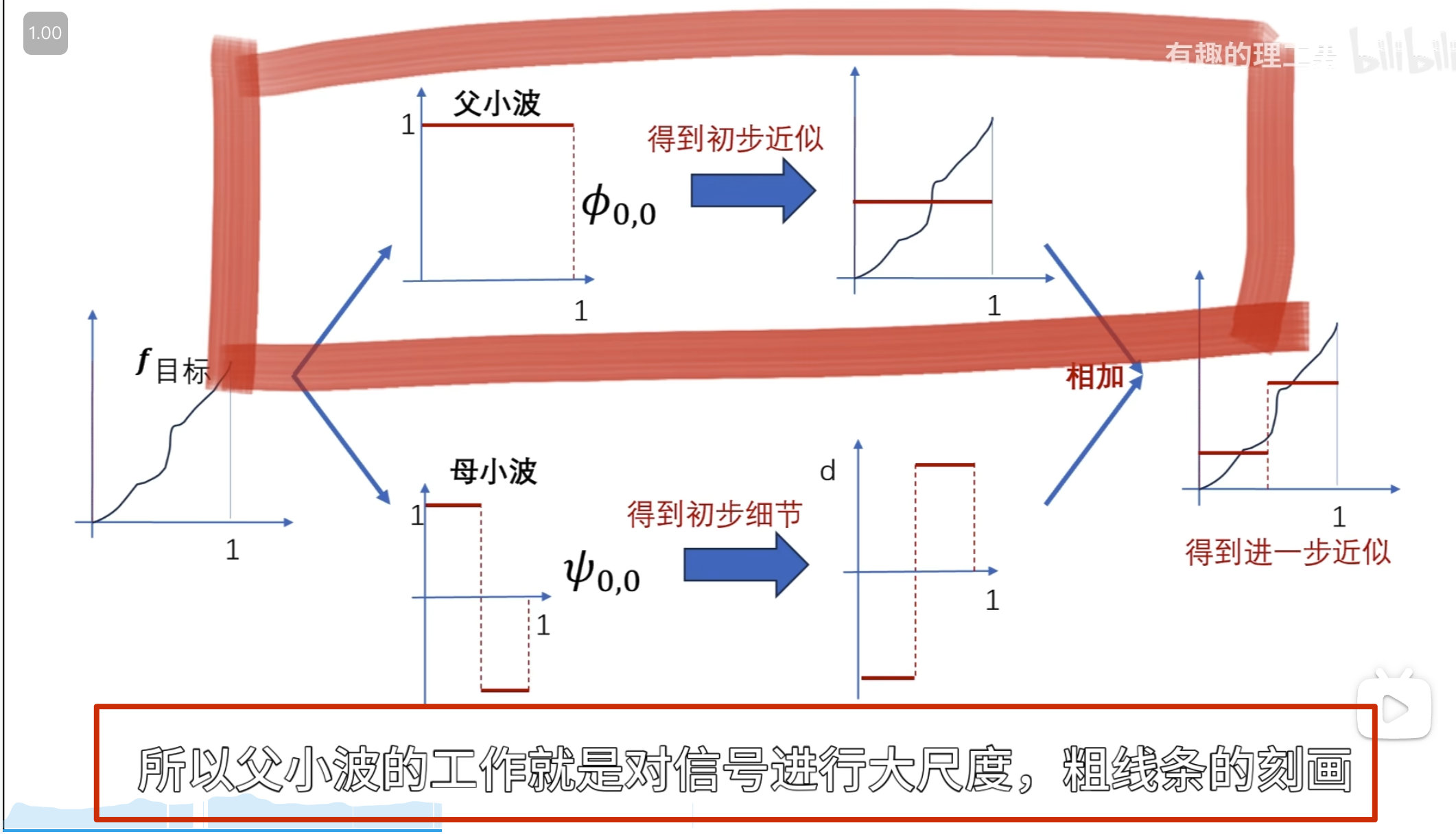
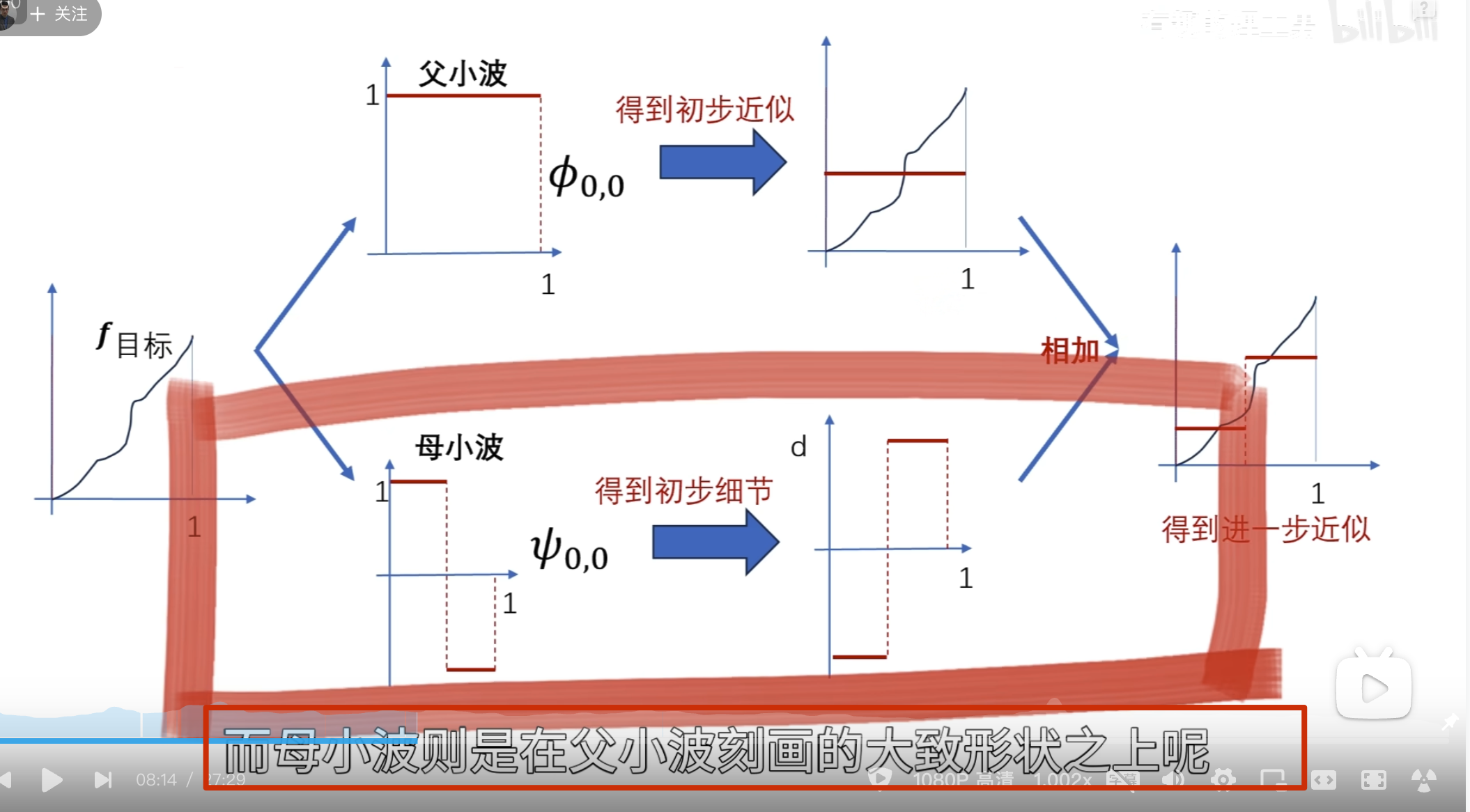
方法一:轮廓加细节



方法二:




这就是 haar 小波
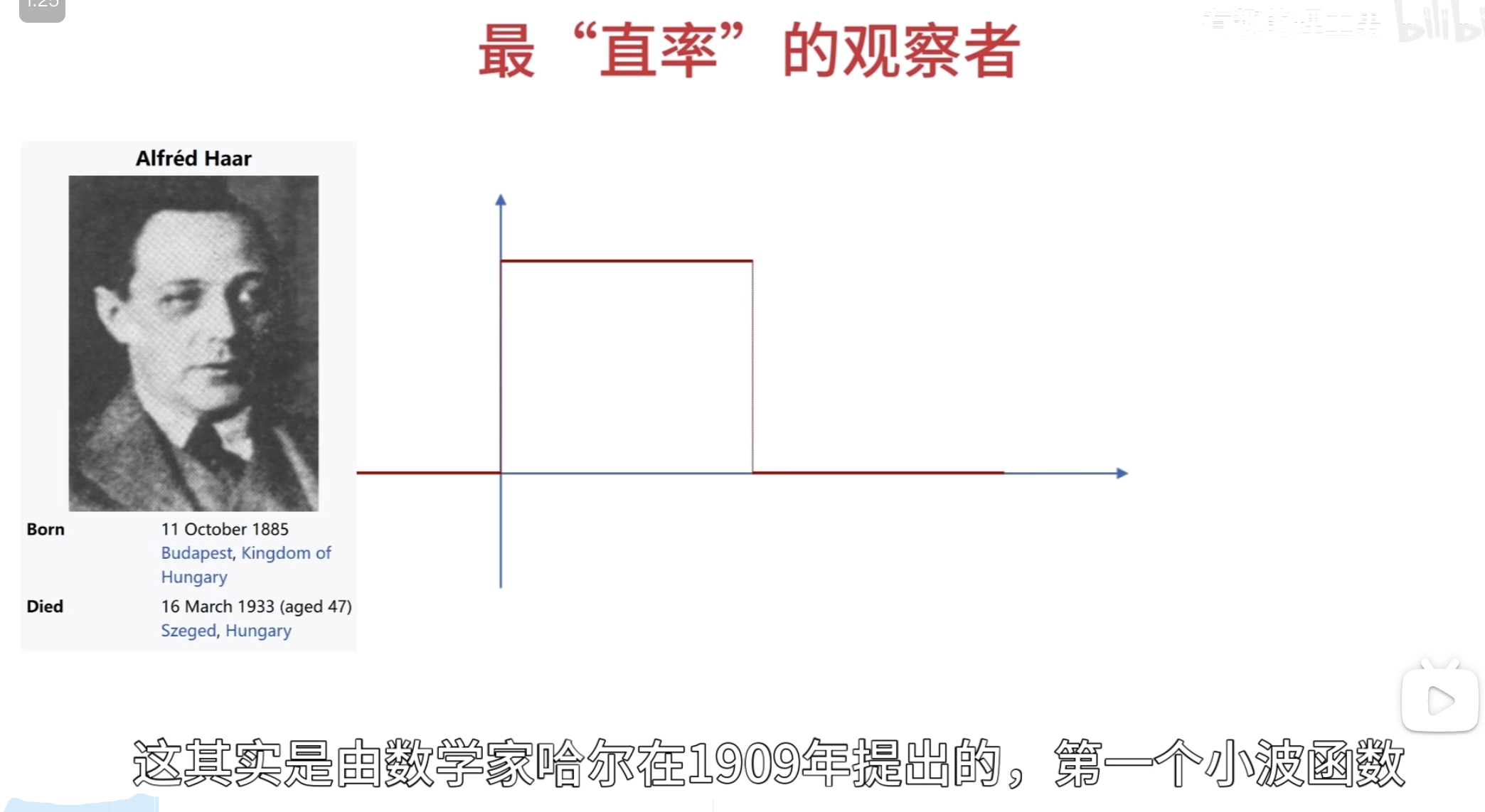
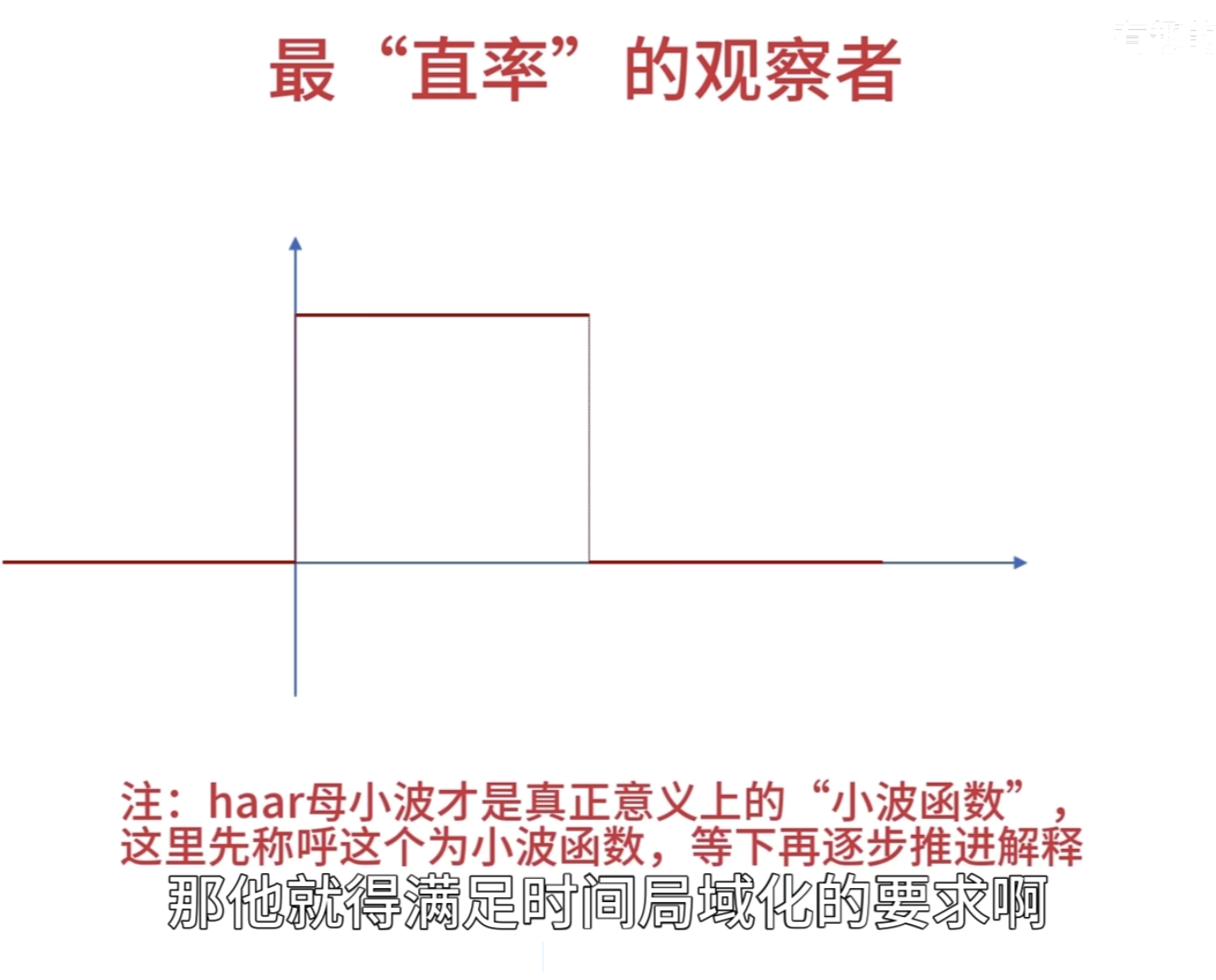
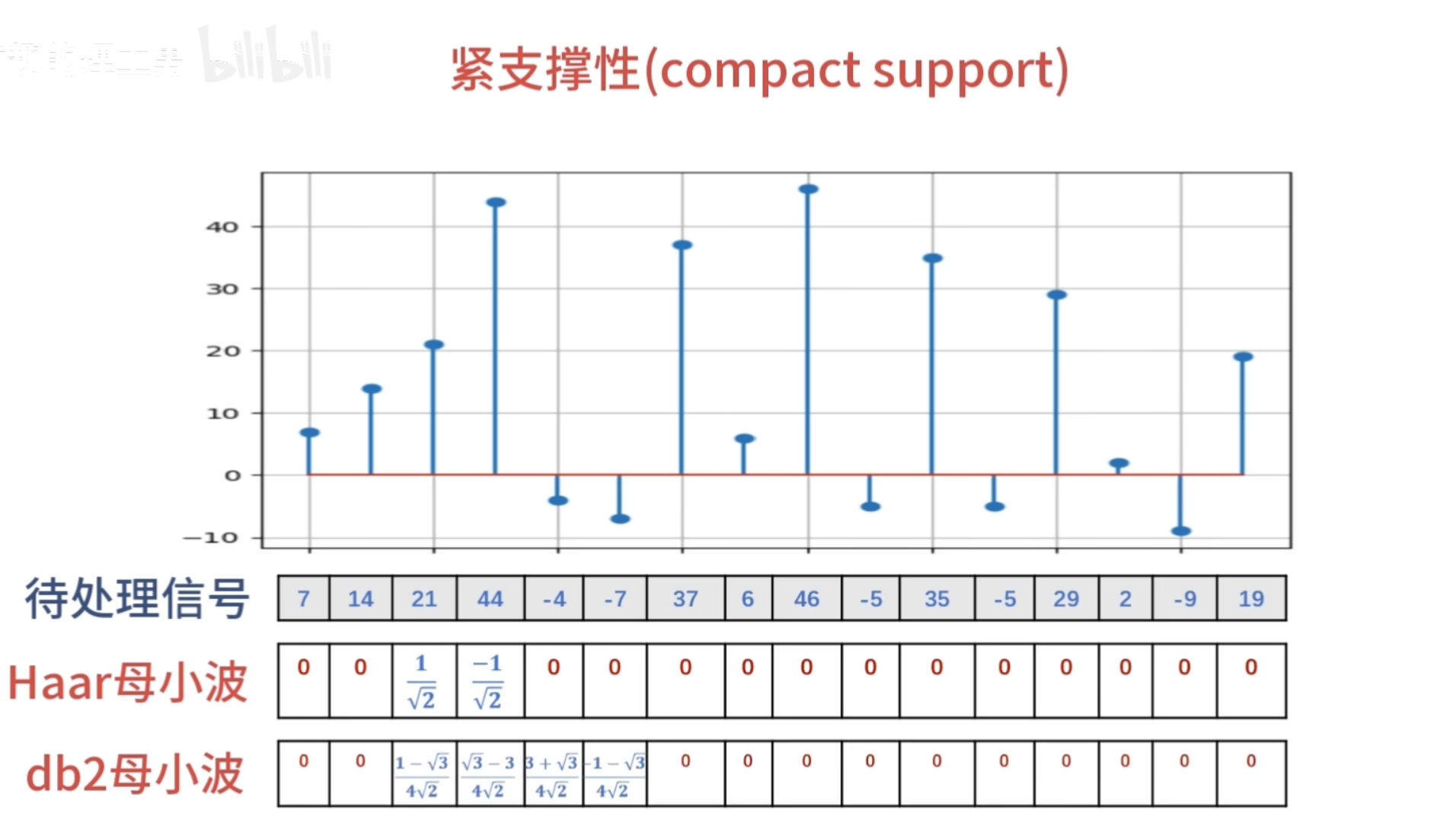
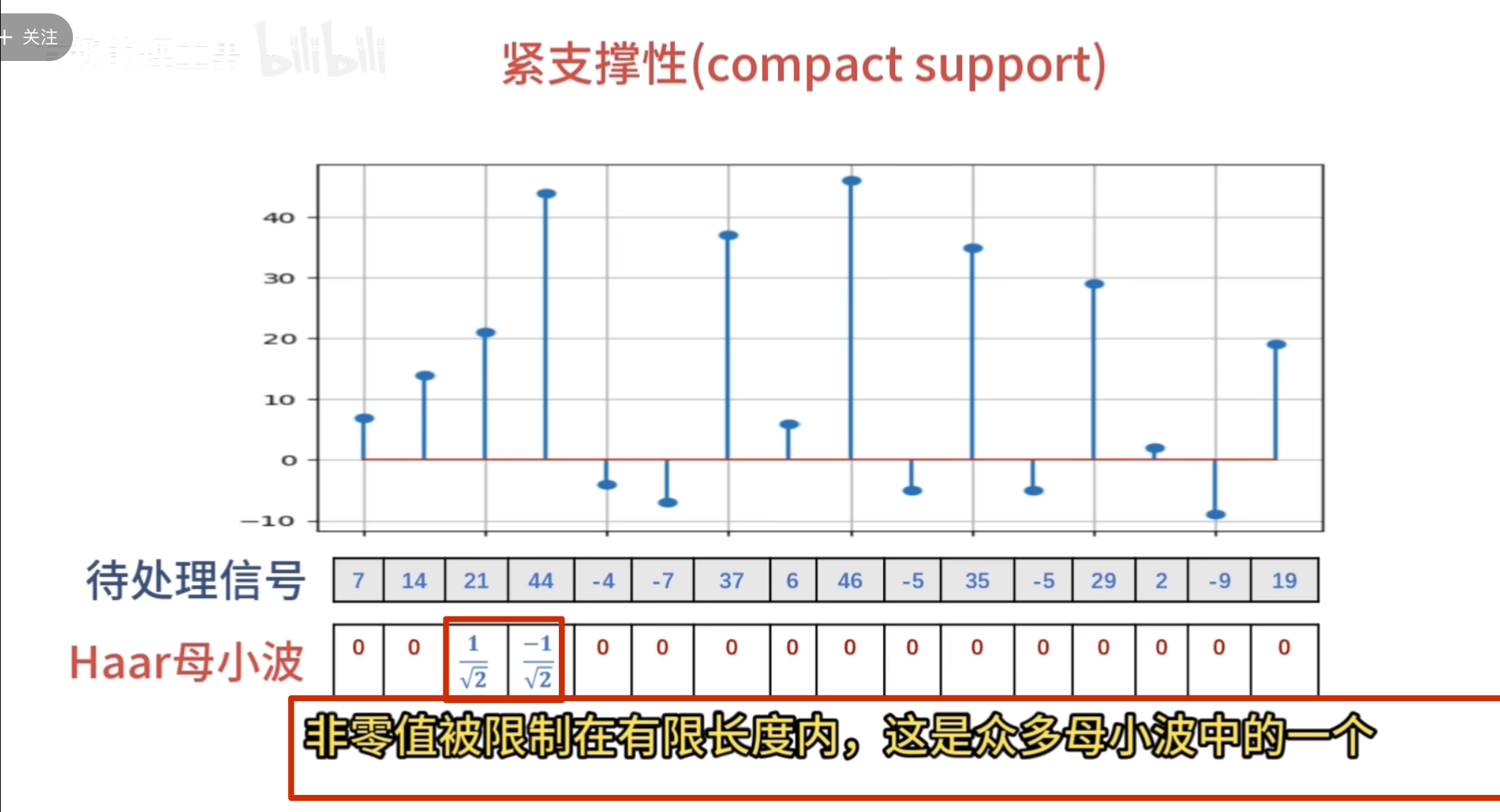
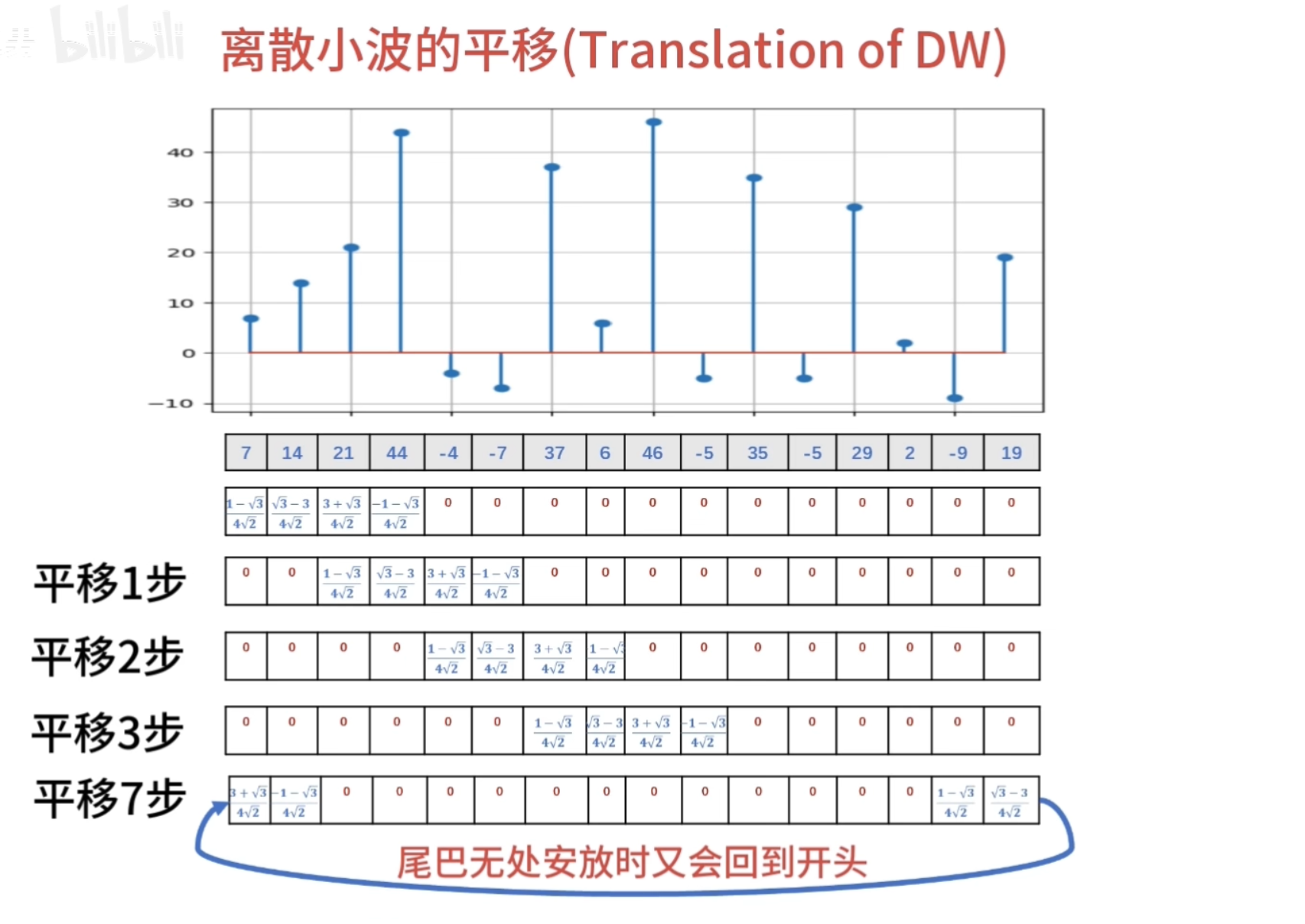
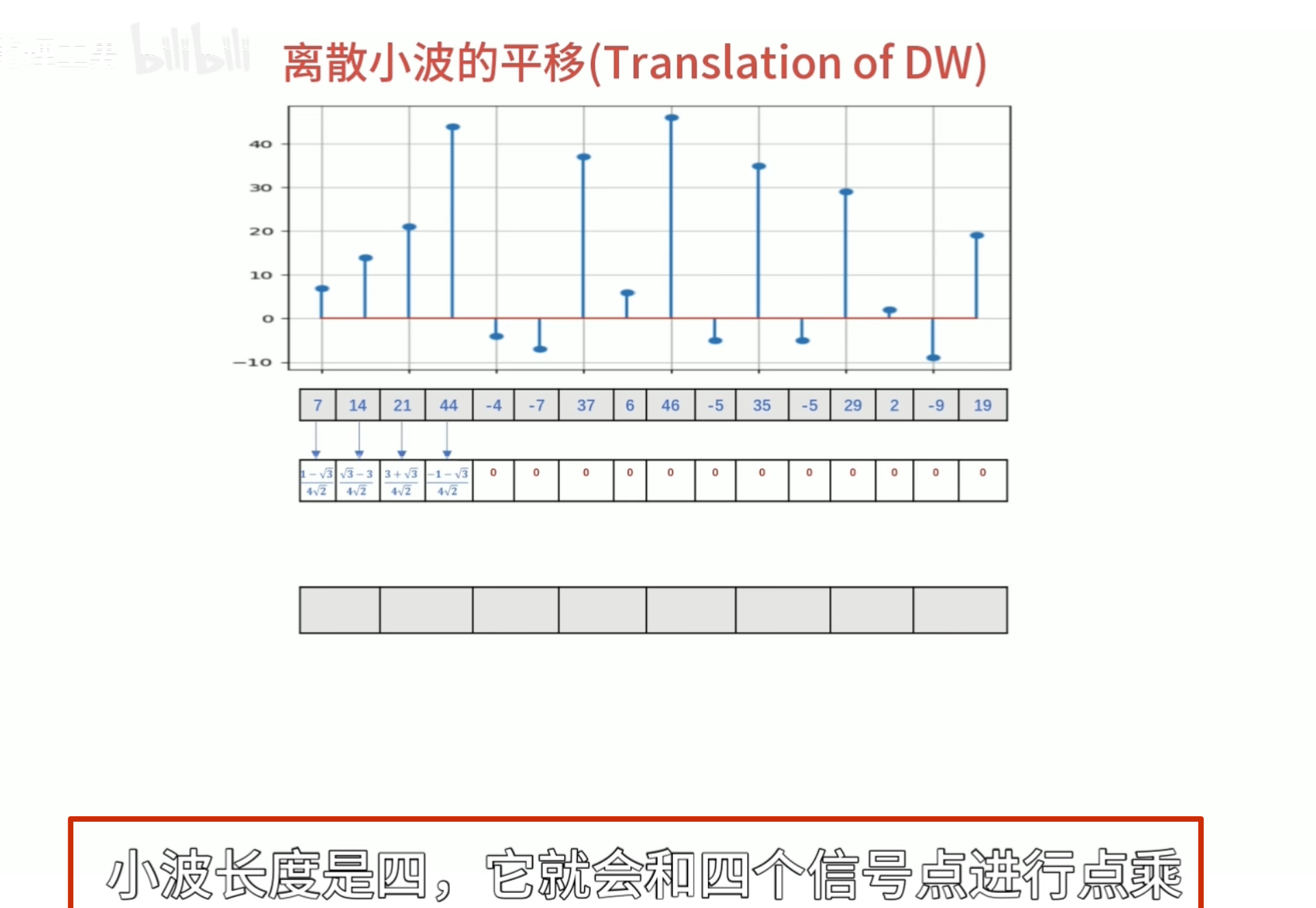
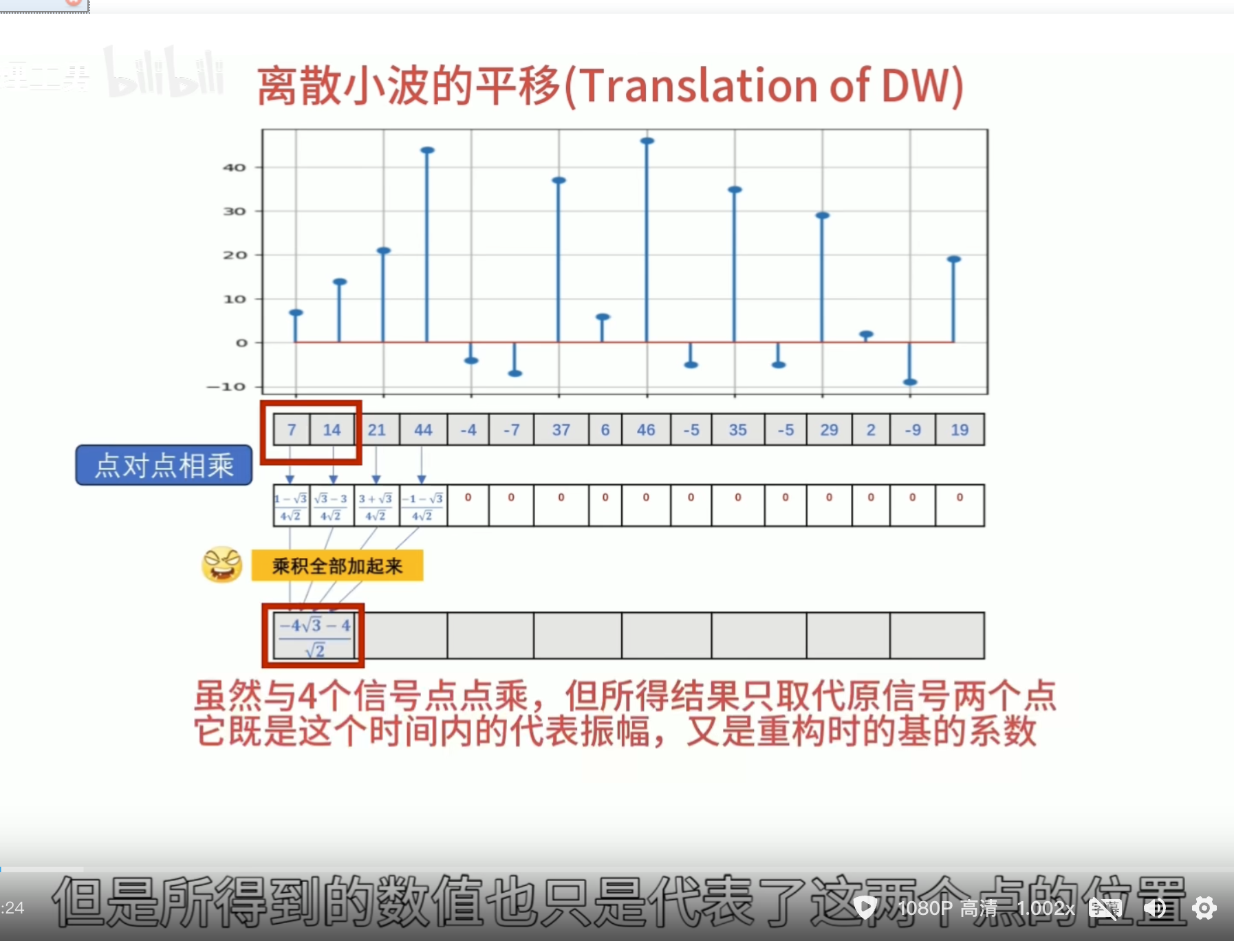
小波函数需要满足时间局域化的要求
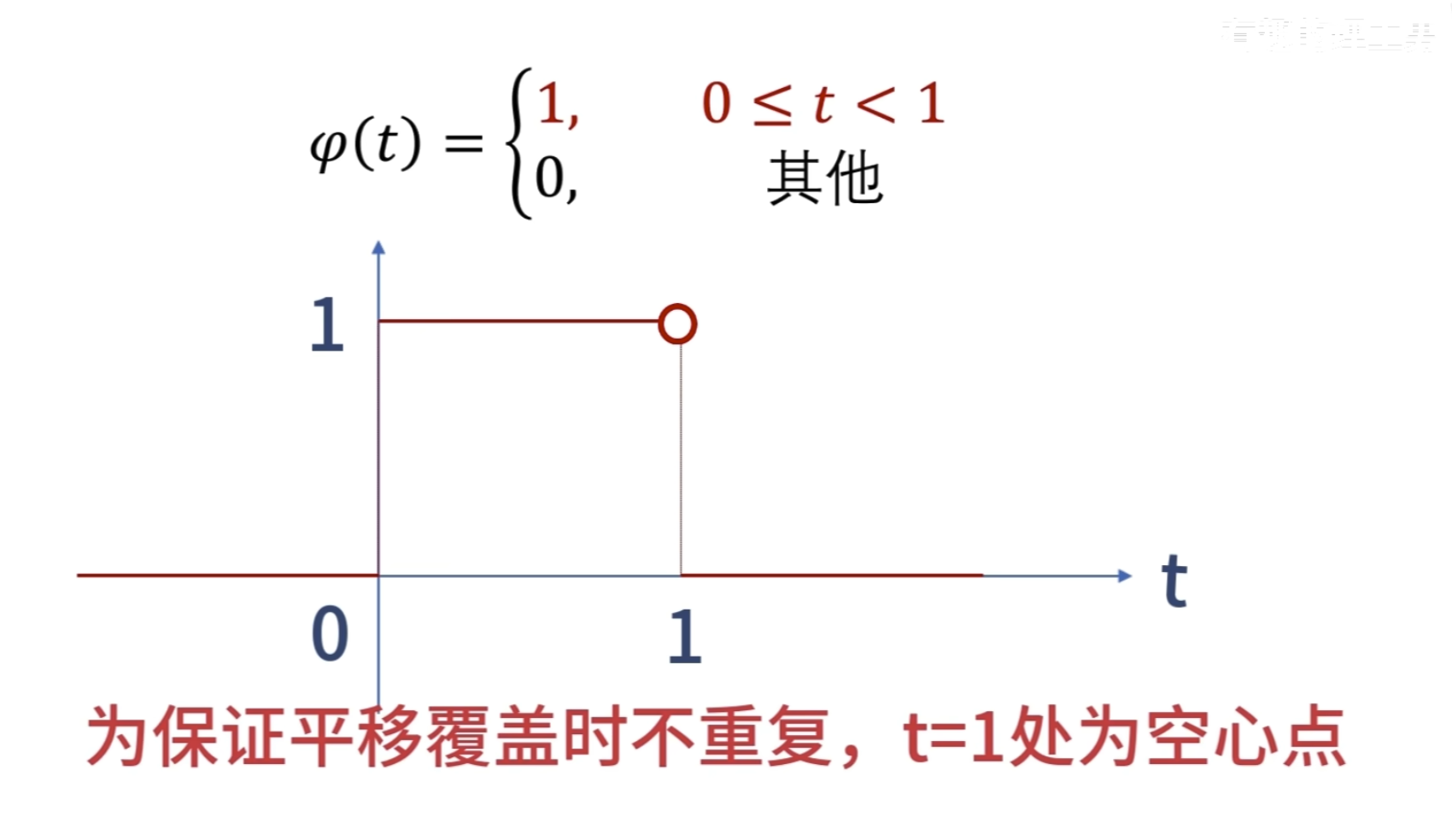
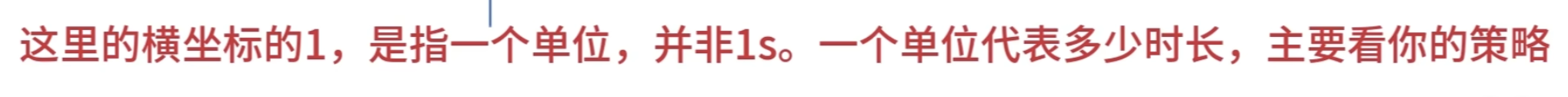
这种仅在某个区域有值,其他区域为 0的性质 数学术语叫做紧支撑性


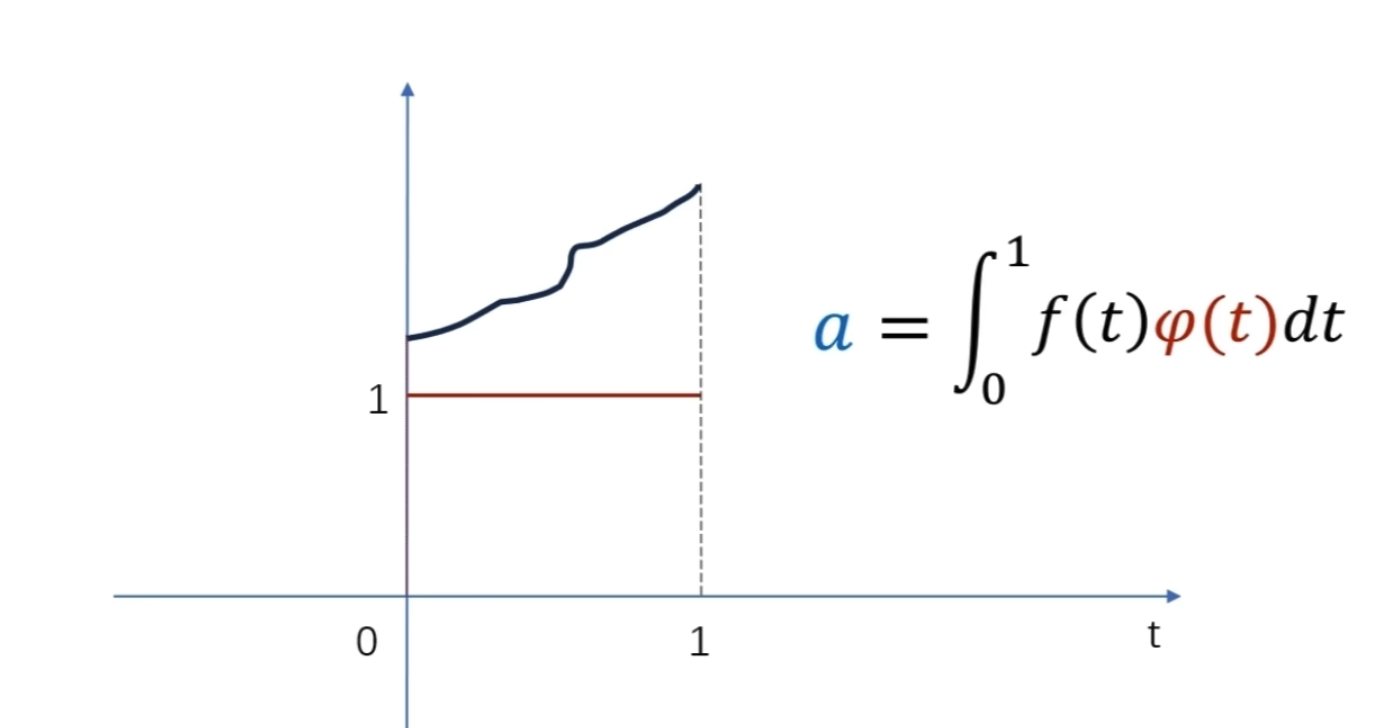
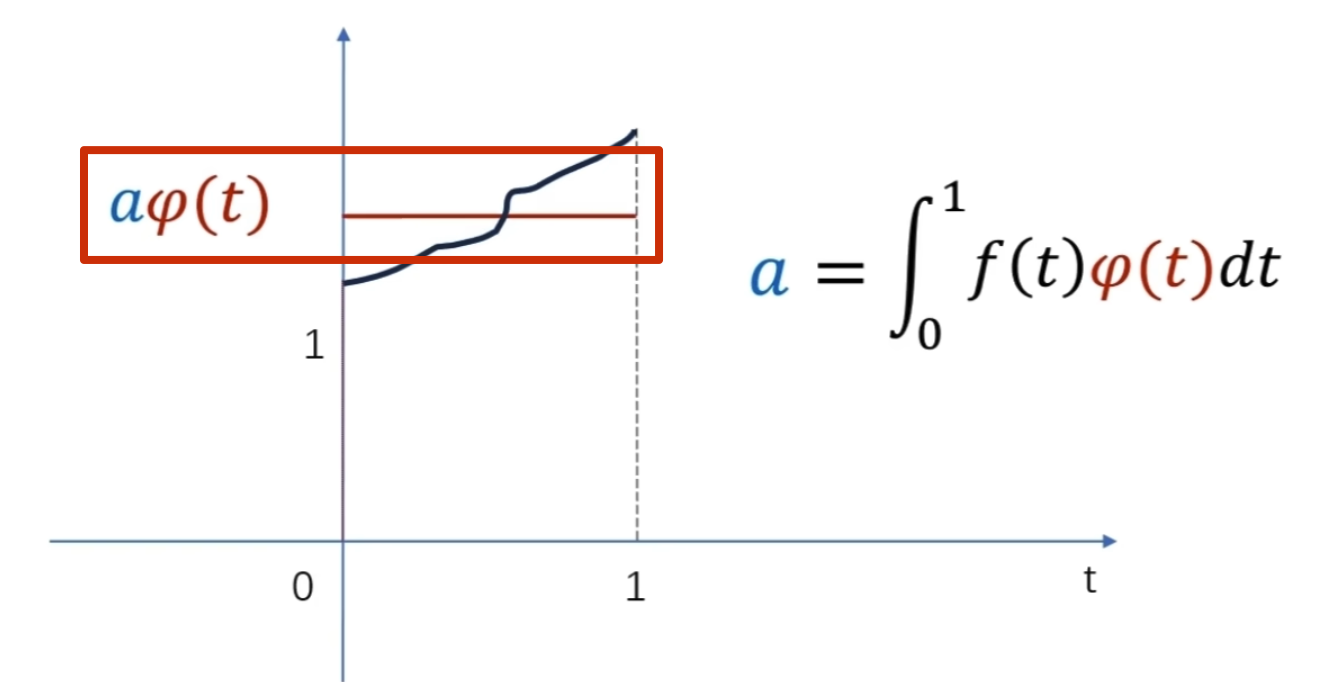
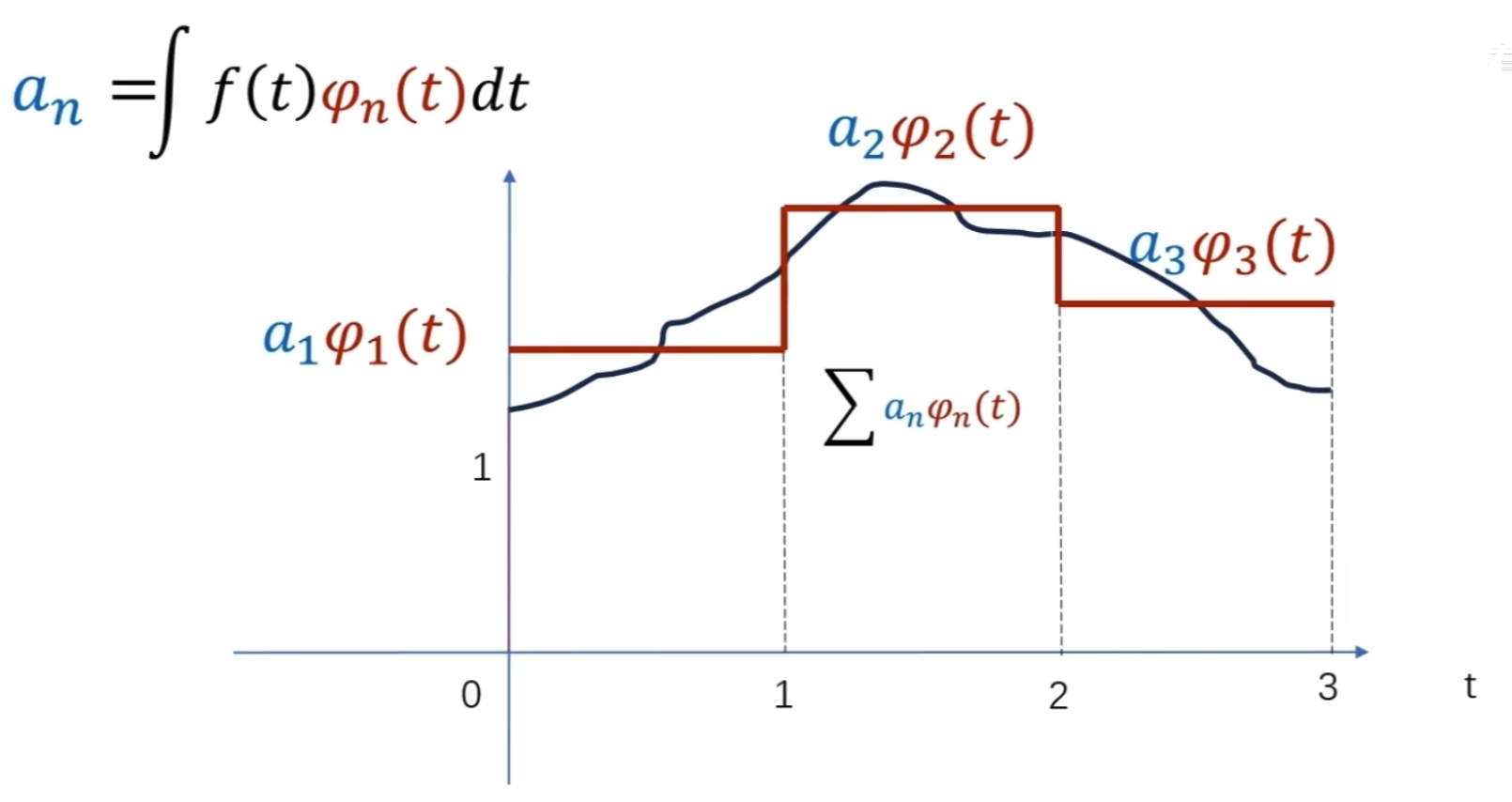
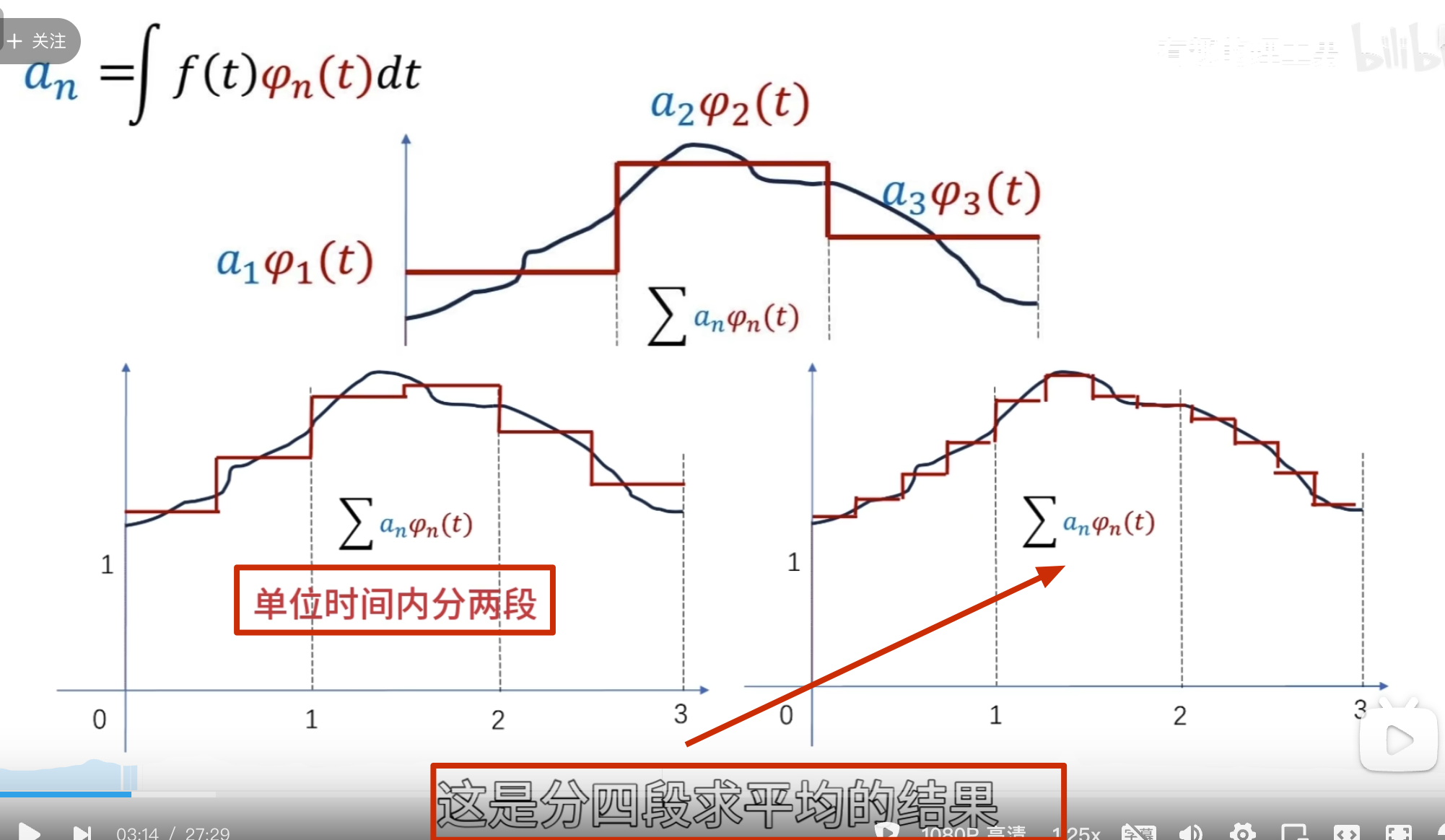
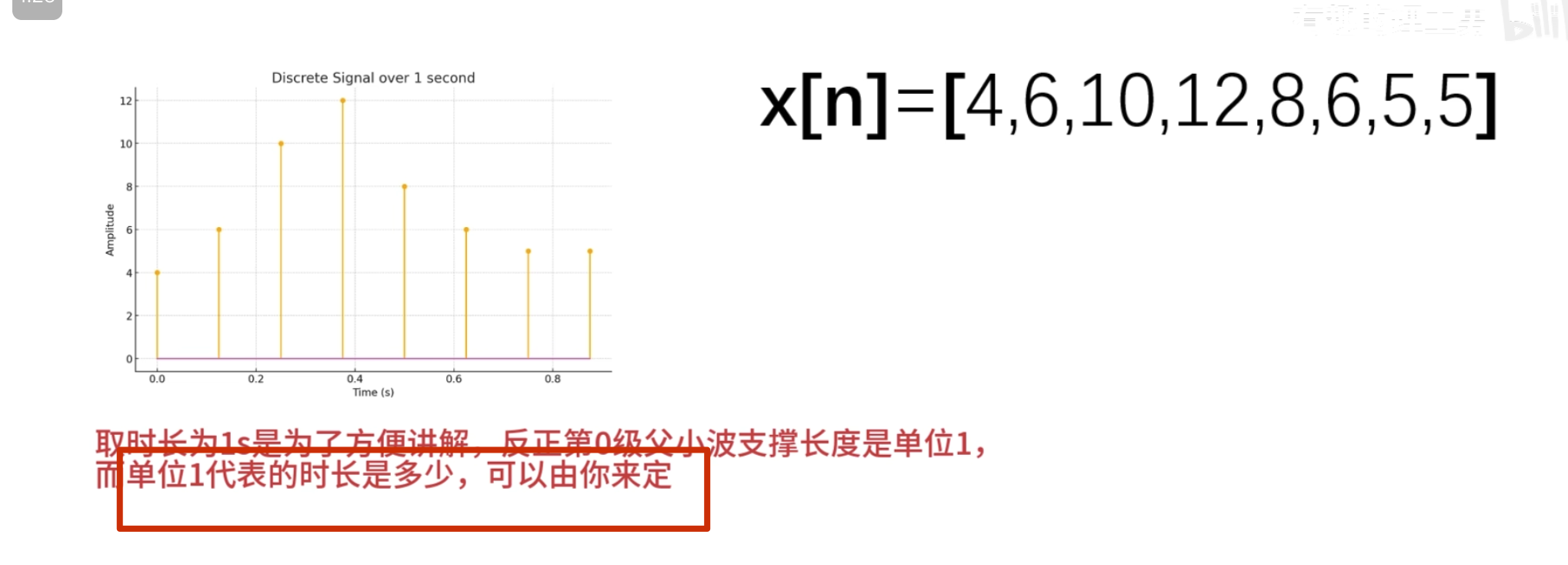
细化的方法采用二分法
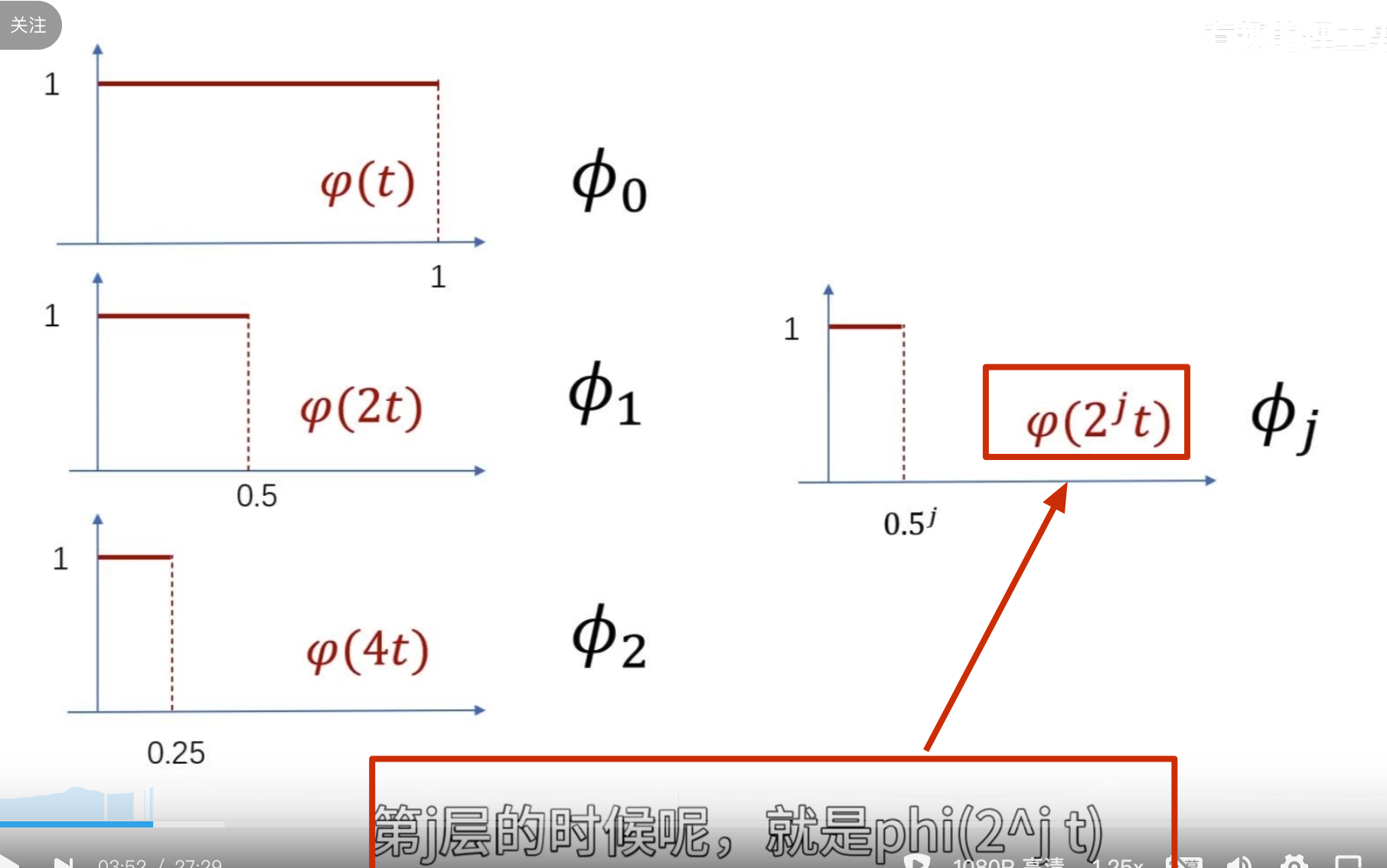

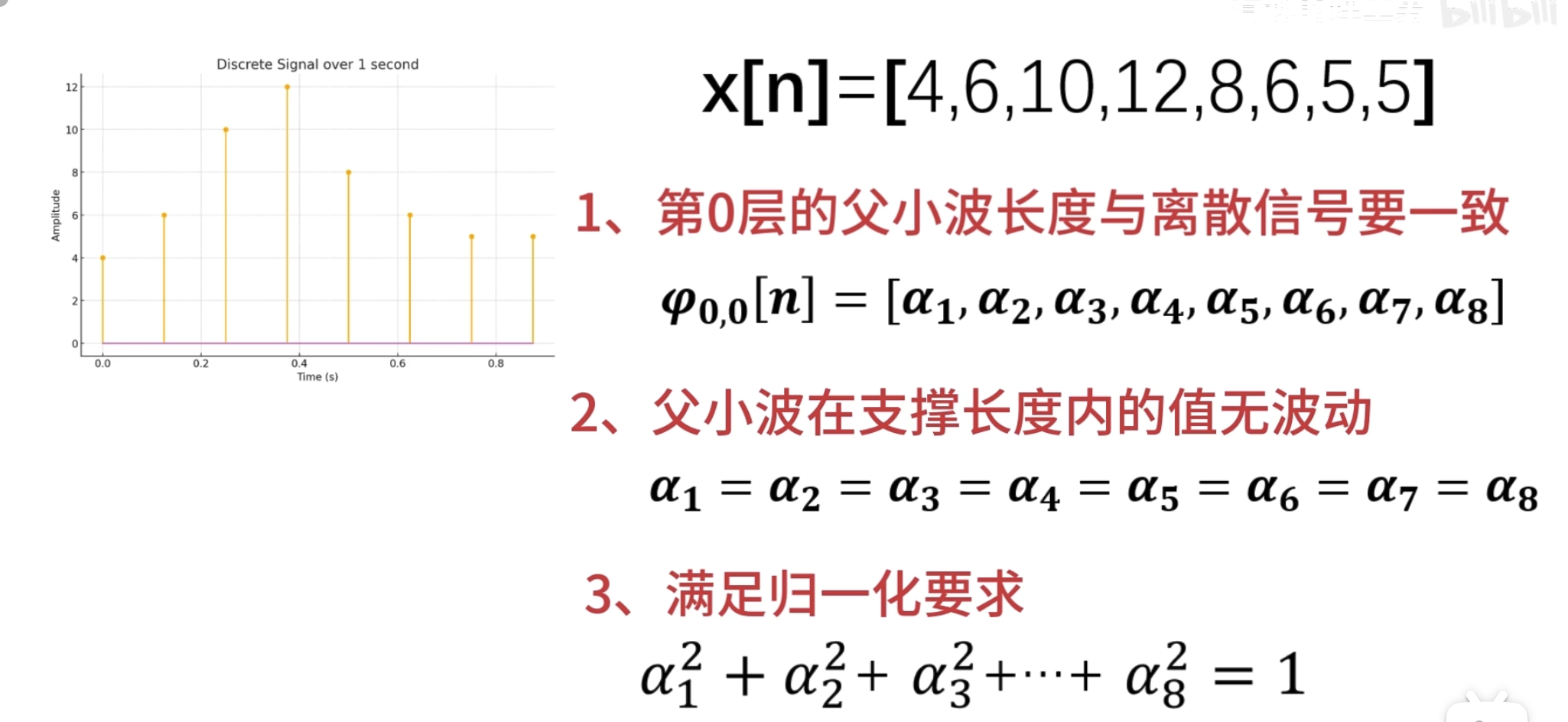
所以这里的 \(\phi_n\)的公式有问题,需要求\(\phi_n\)的公式(重点啊,不然后面看不懂了)

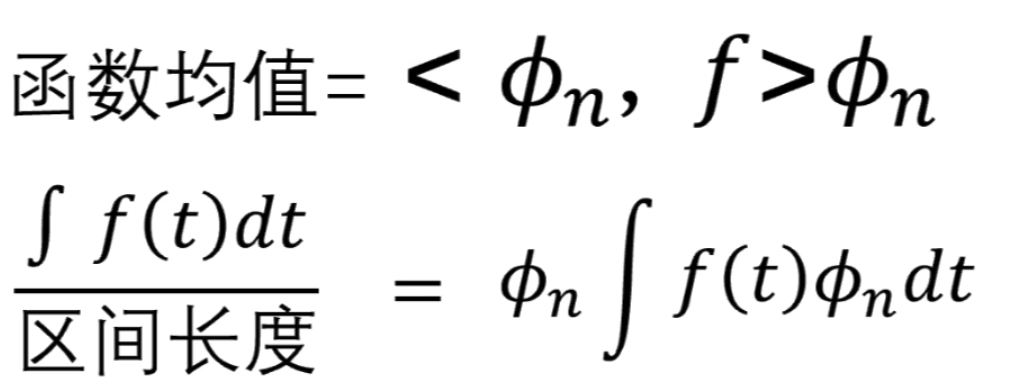

 ,可以提出来
,可以提出来
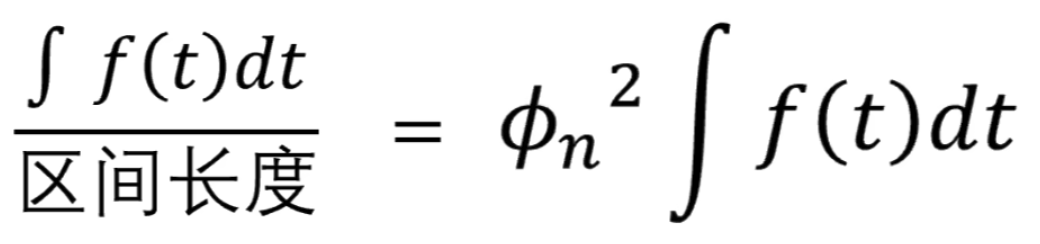
所以可以得出

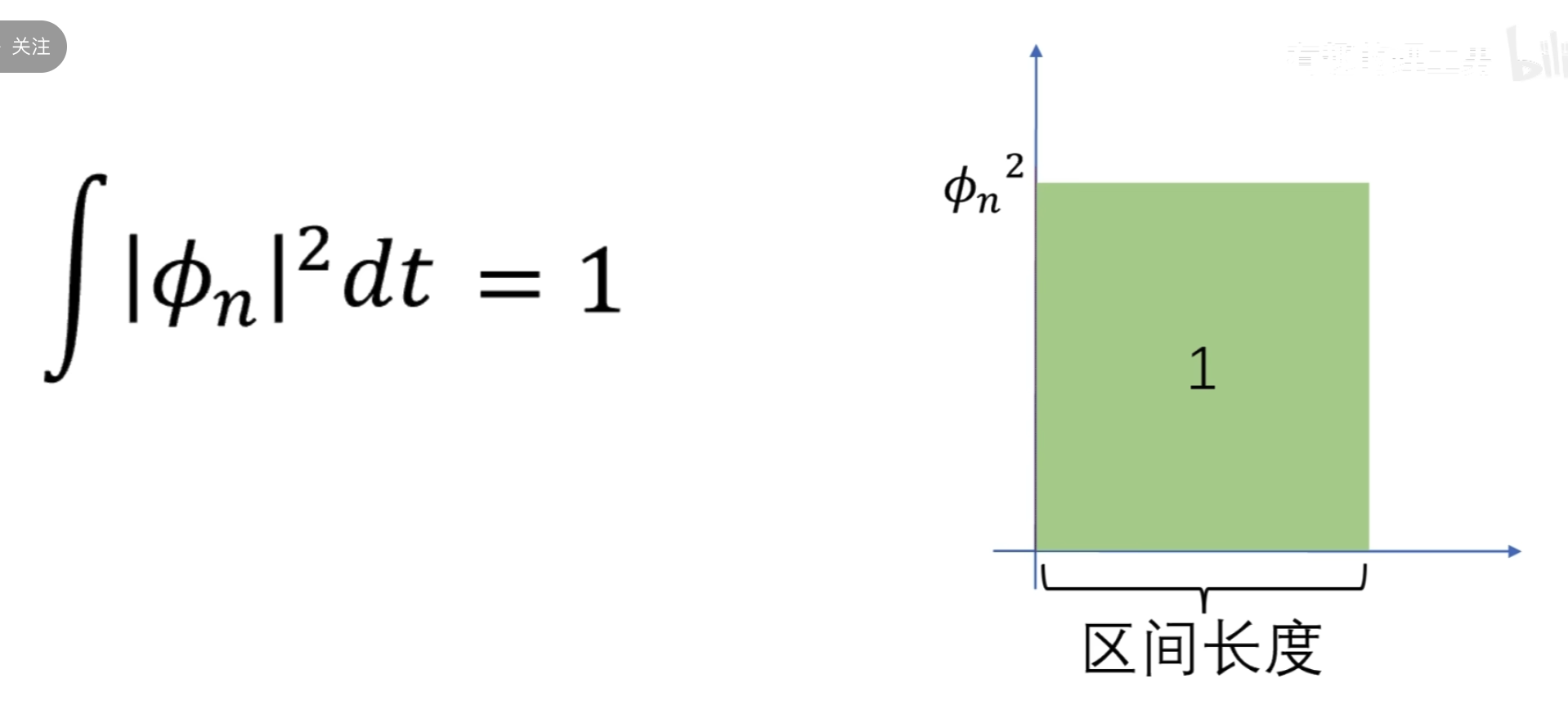






所以归一化后有
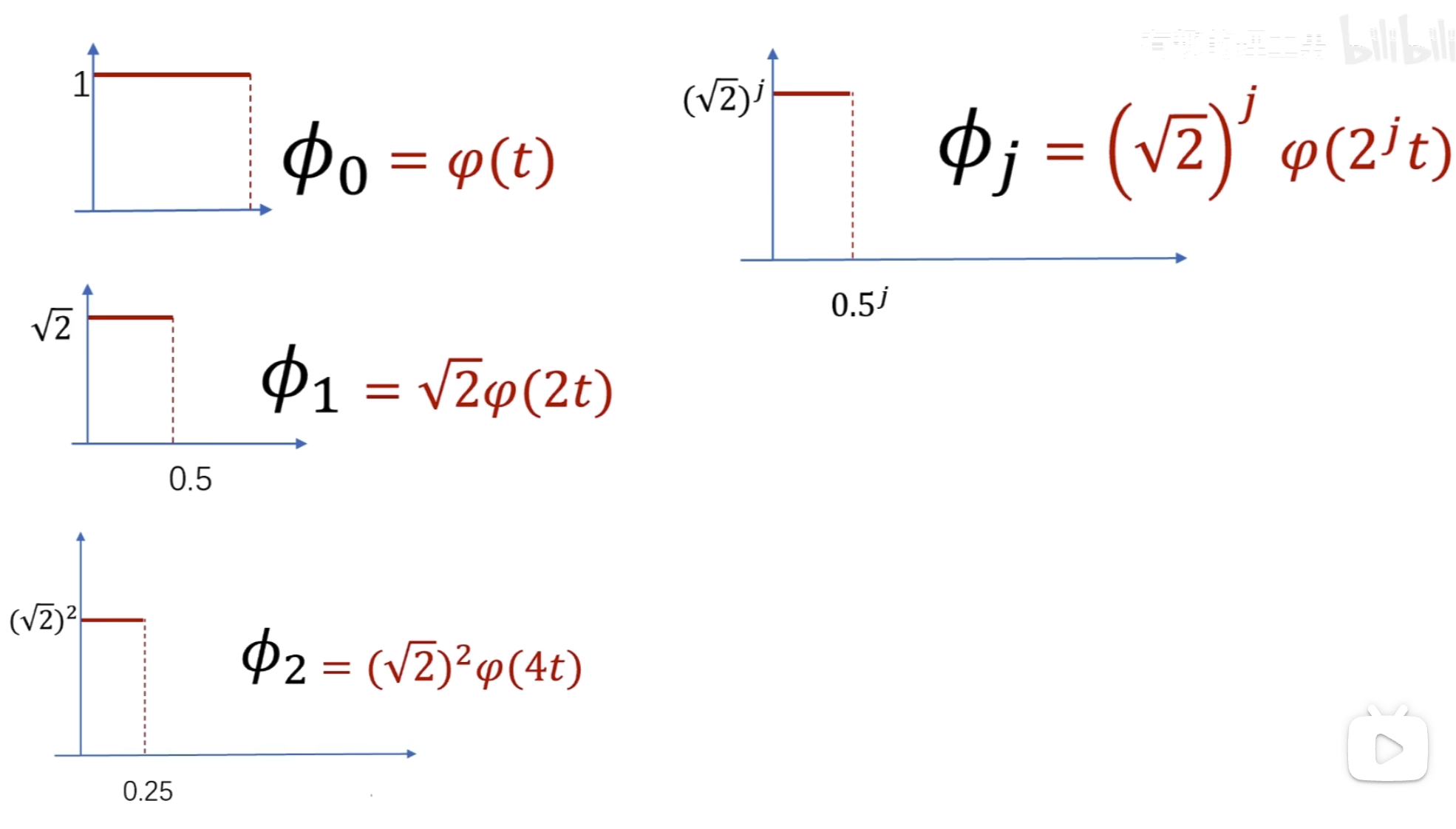

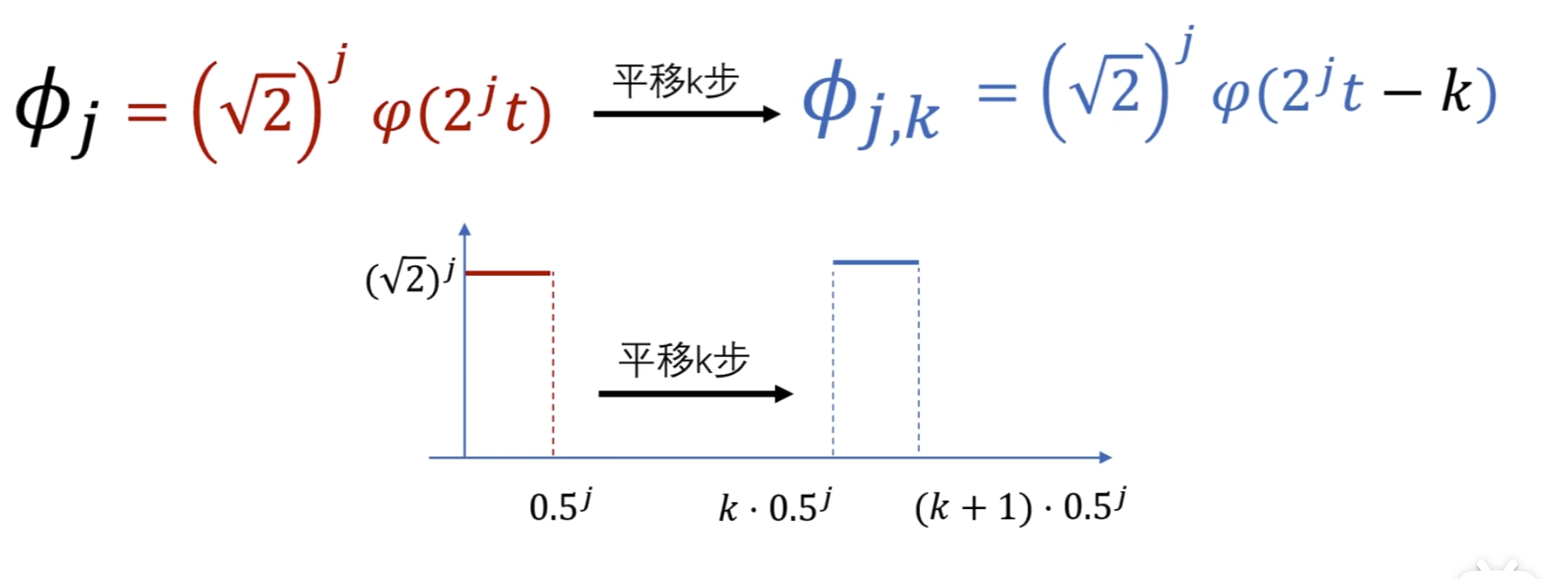

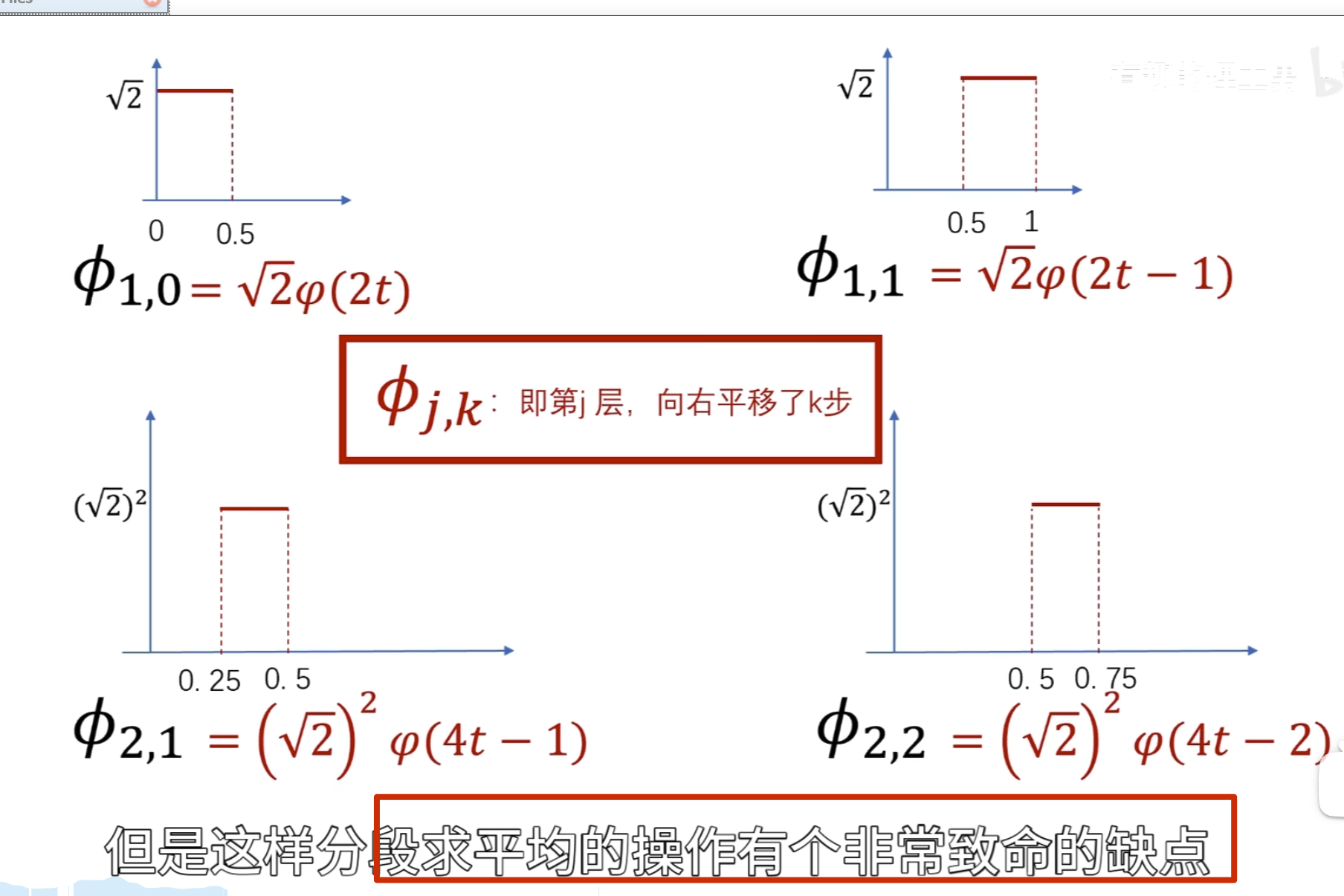
如下所示
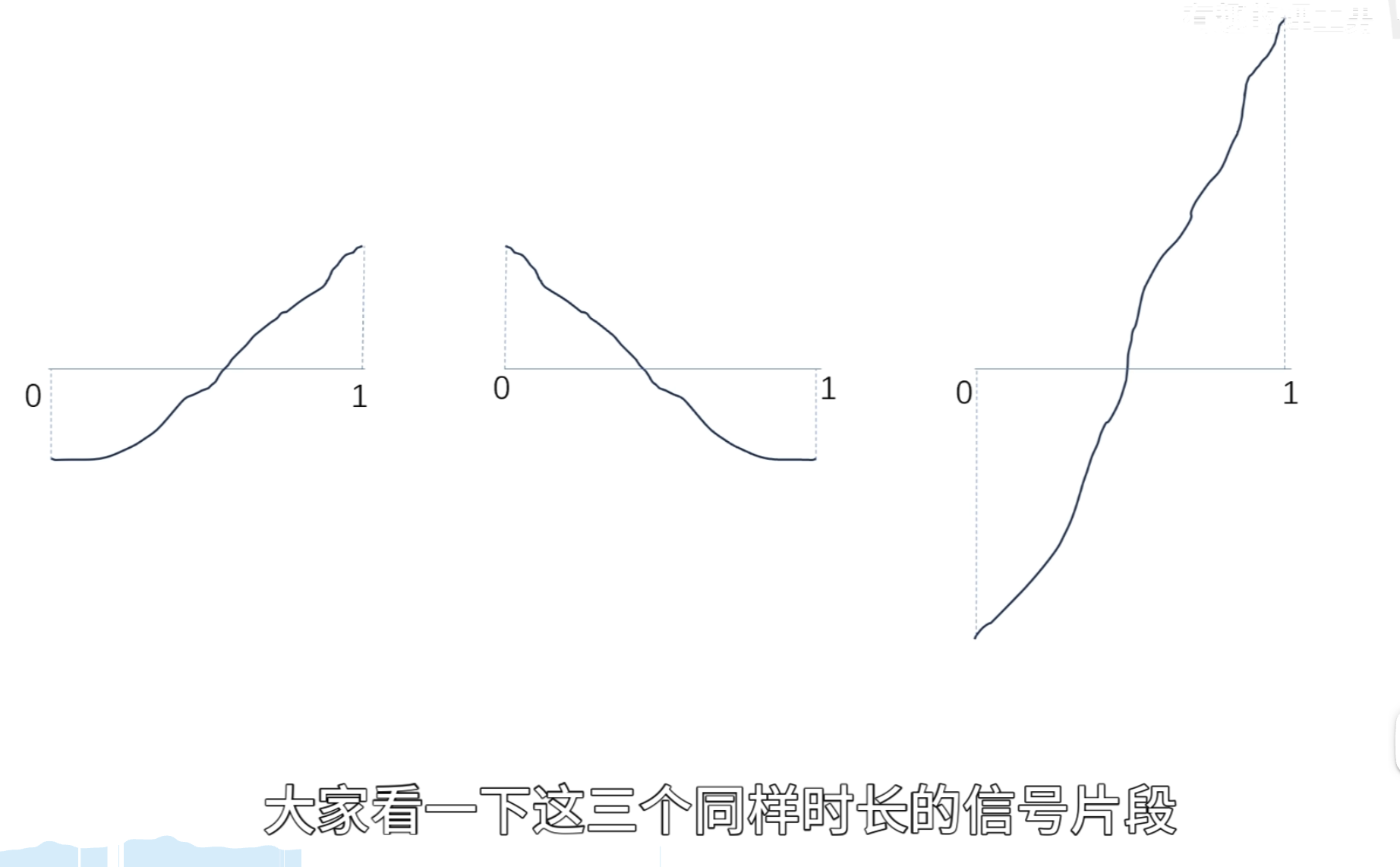






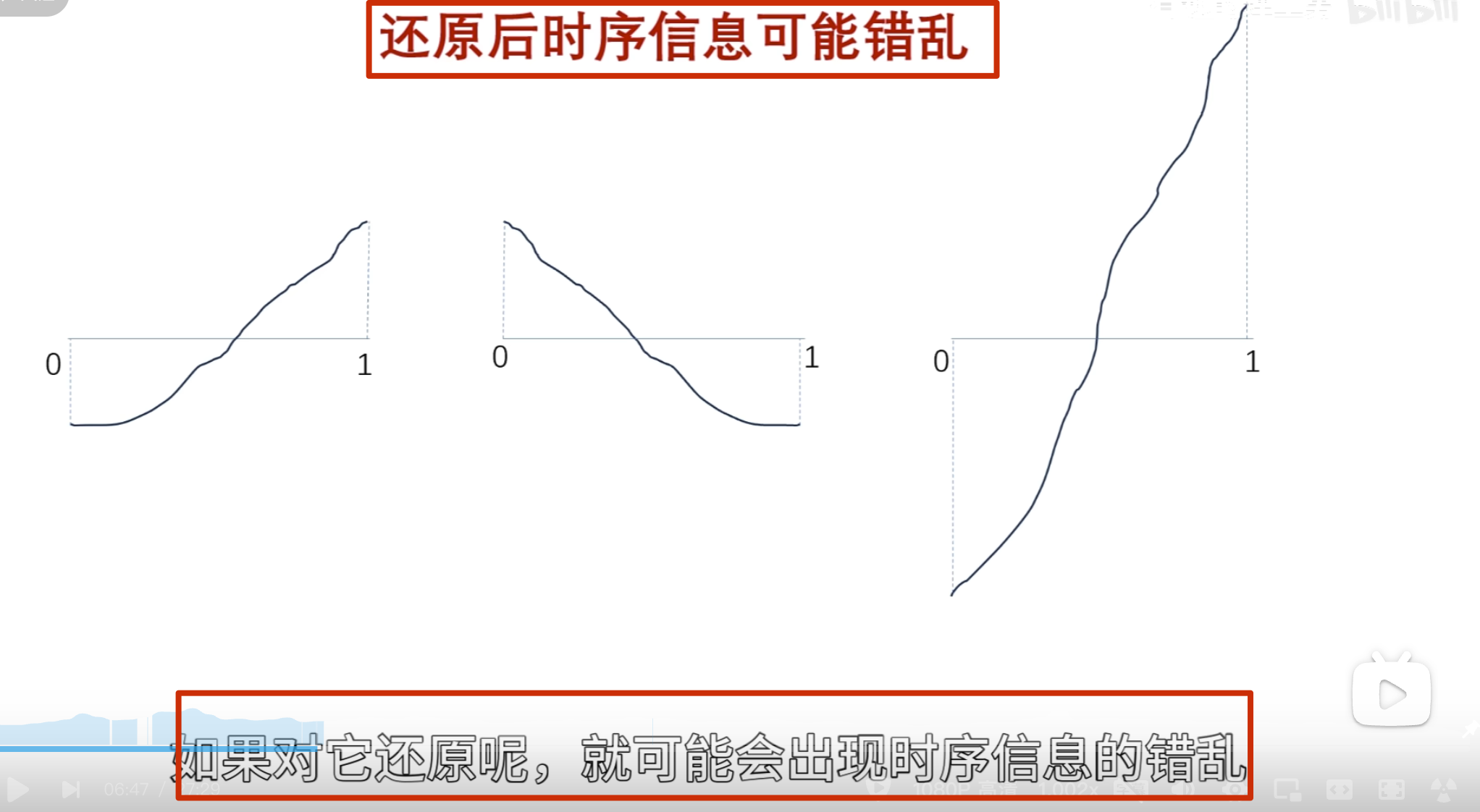
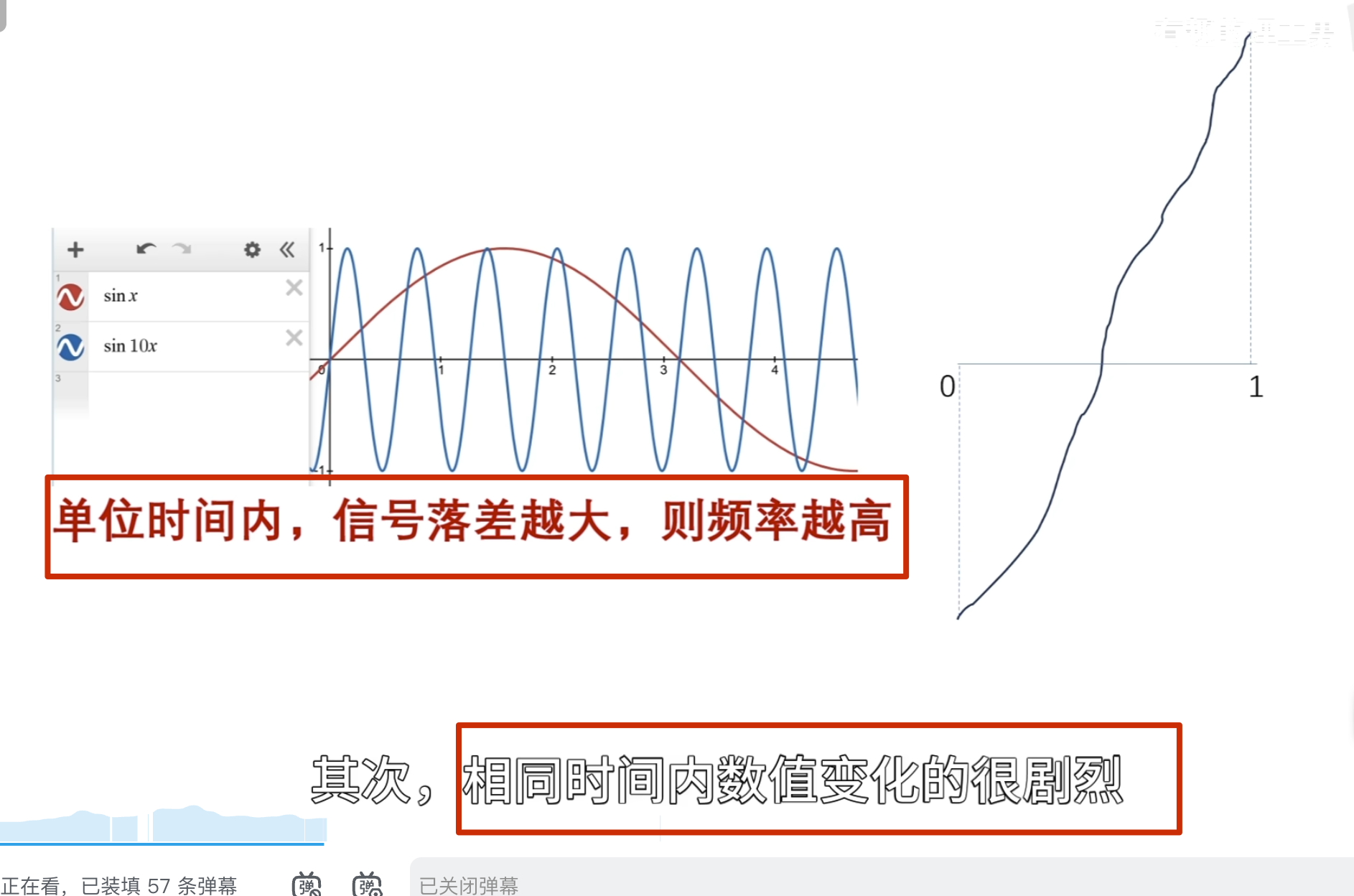






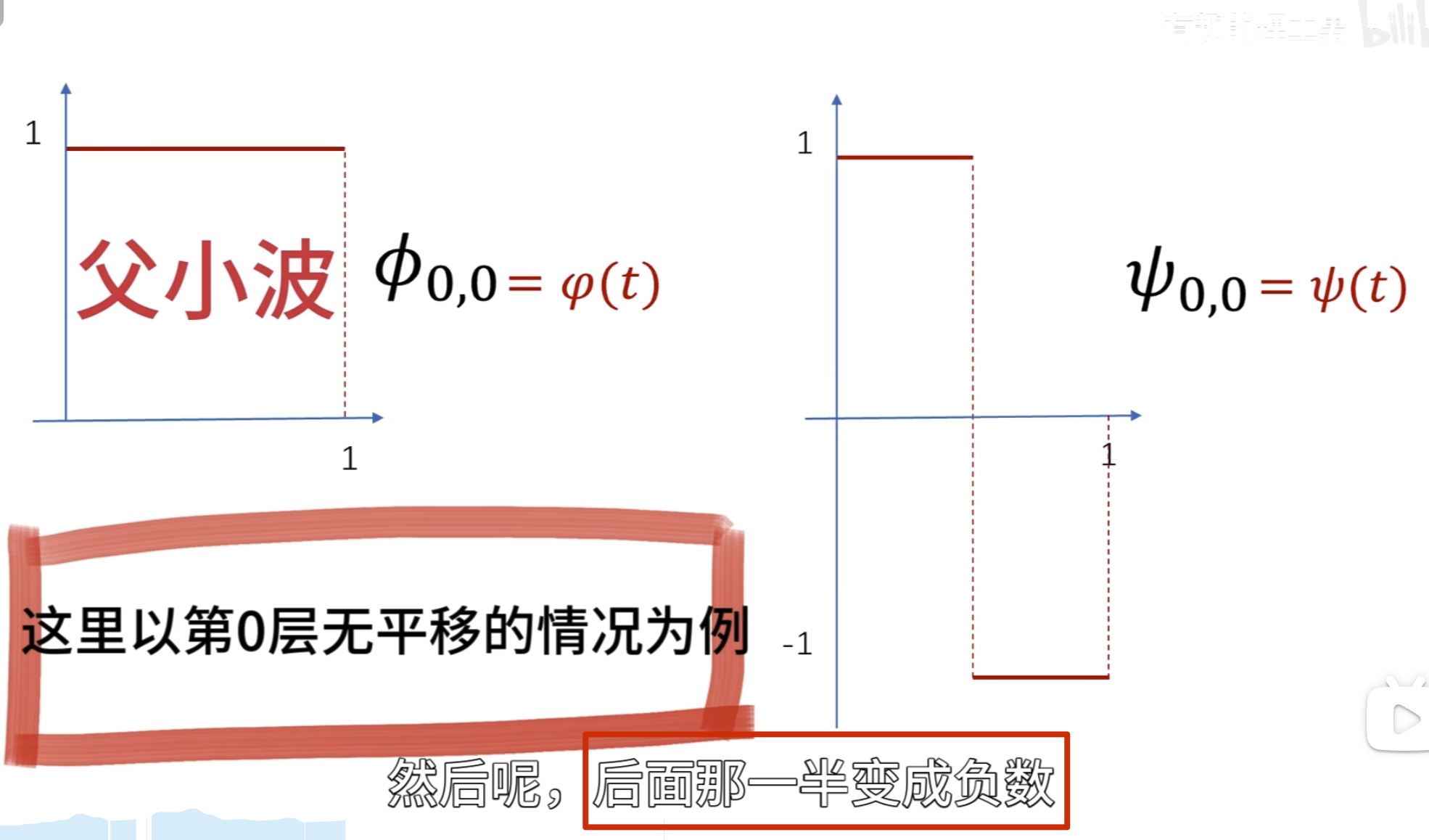
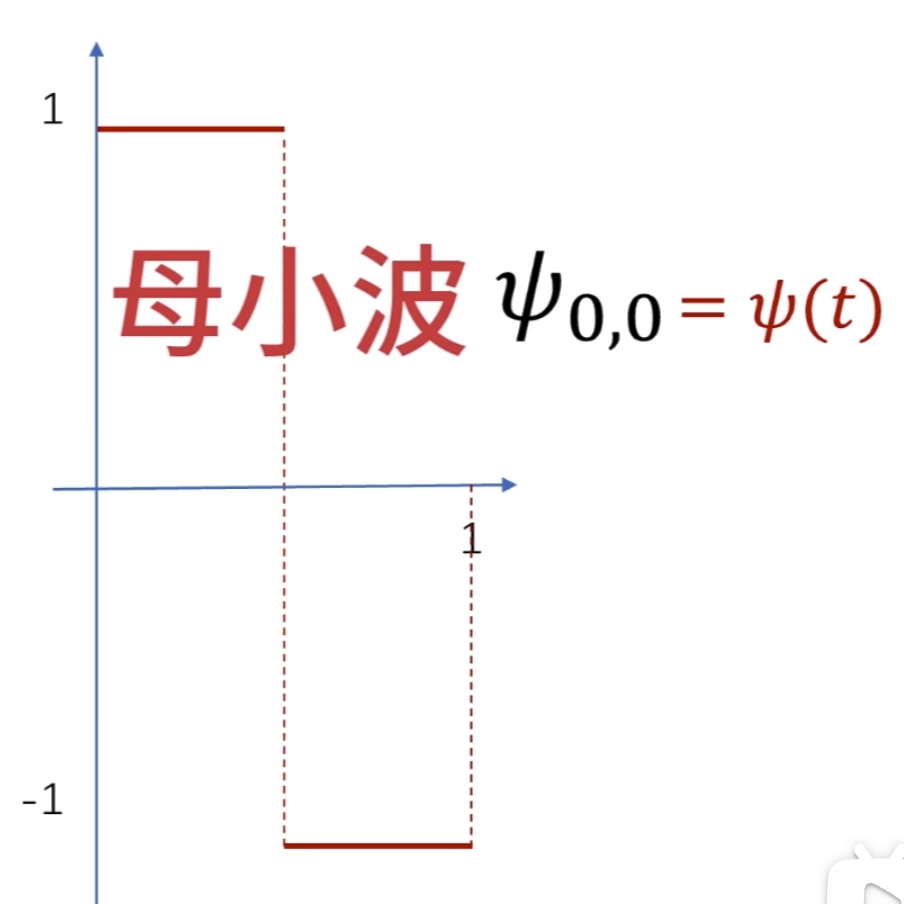
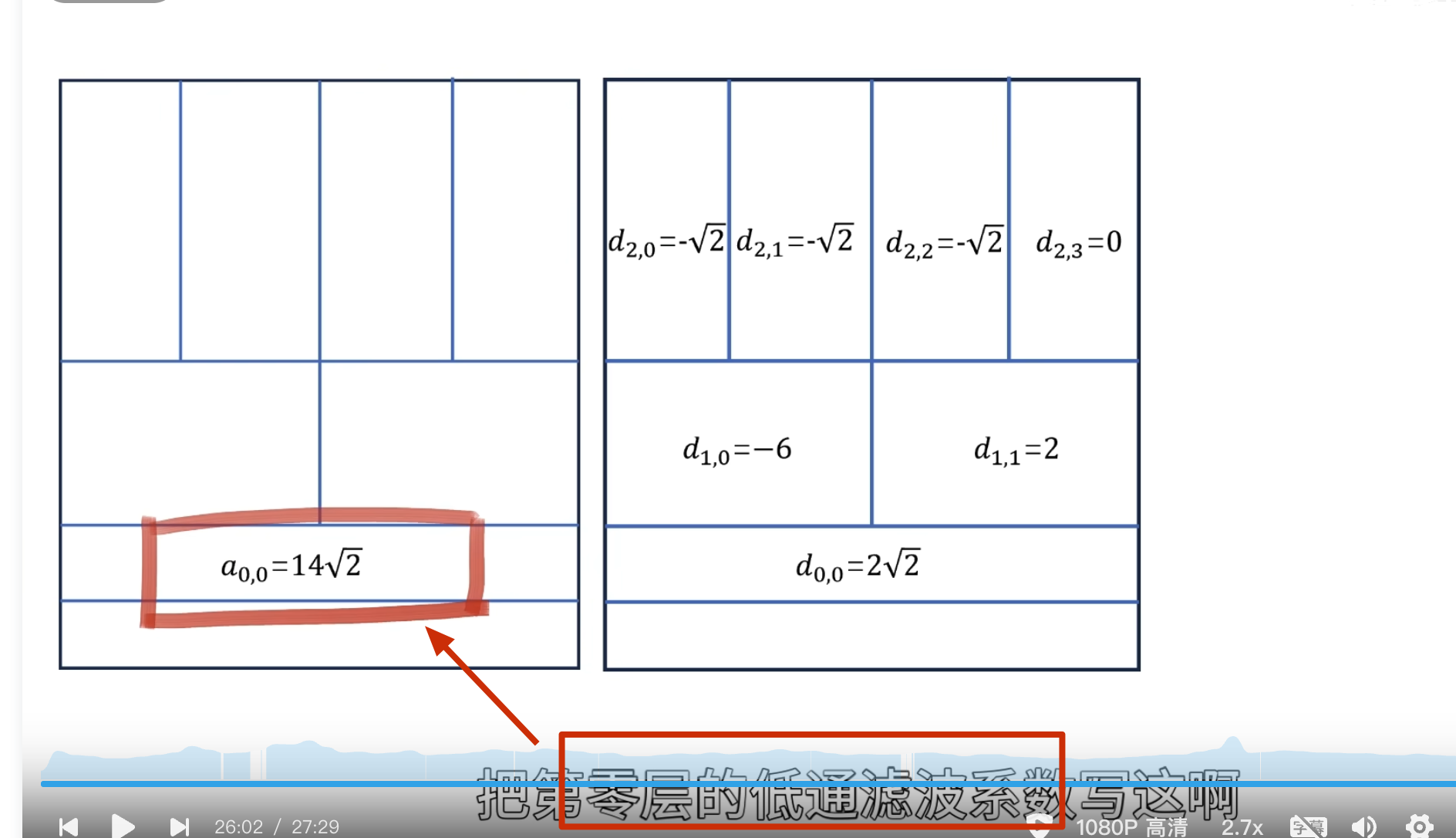
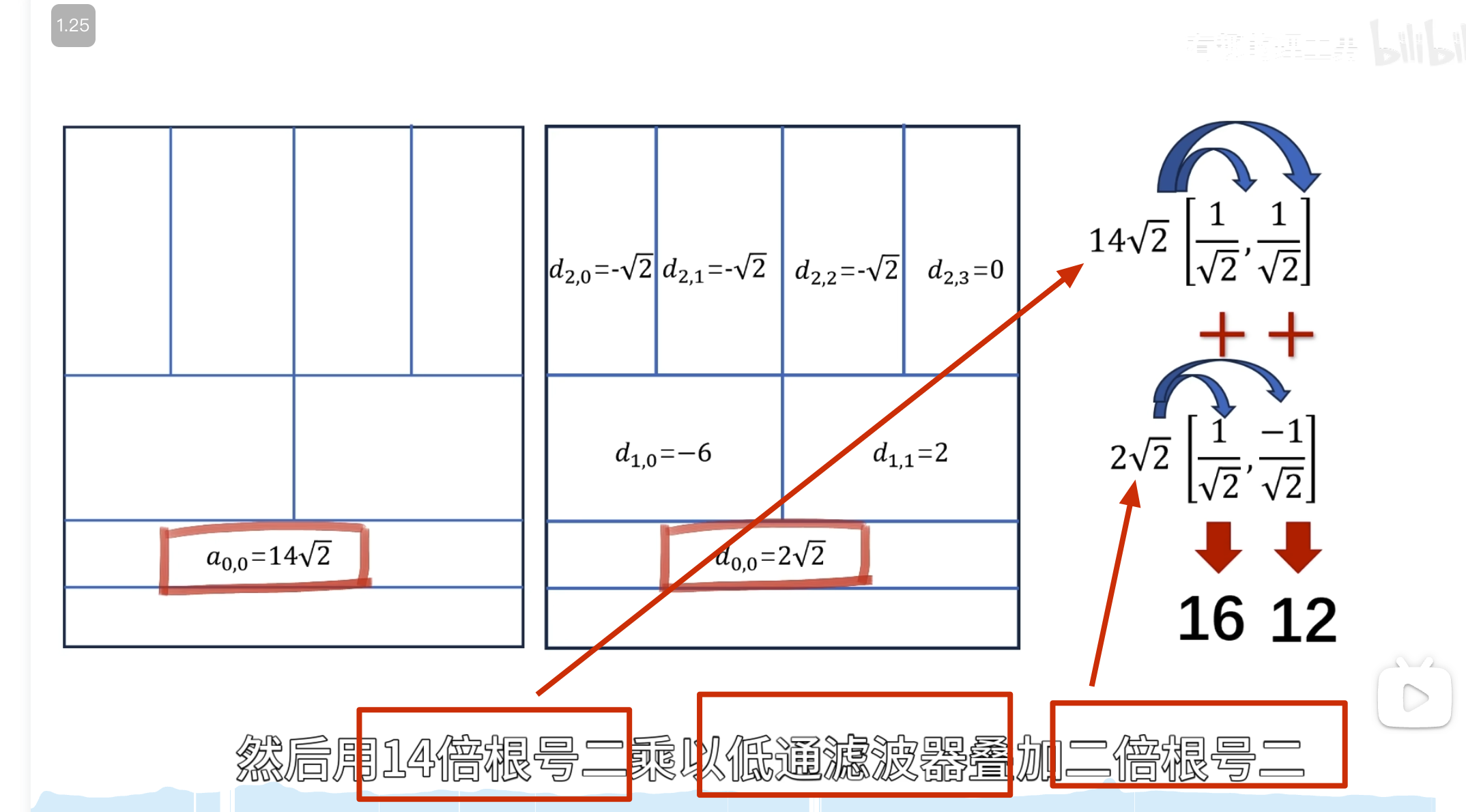
给个例子看是如何解决这个问题的:
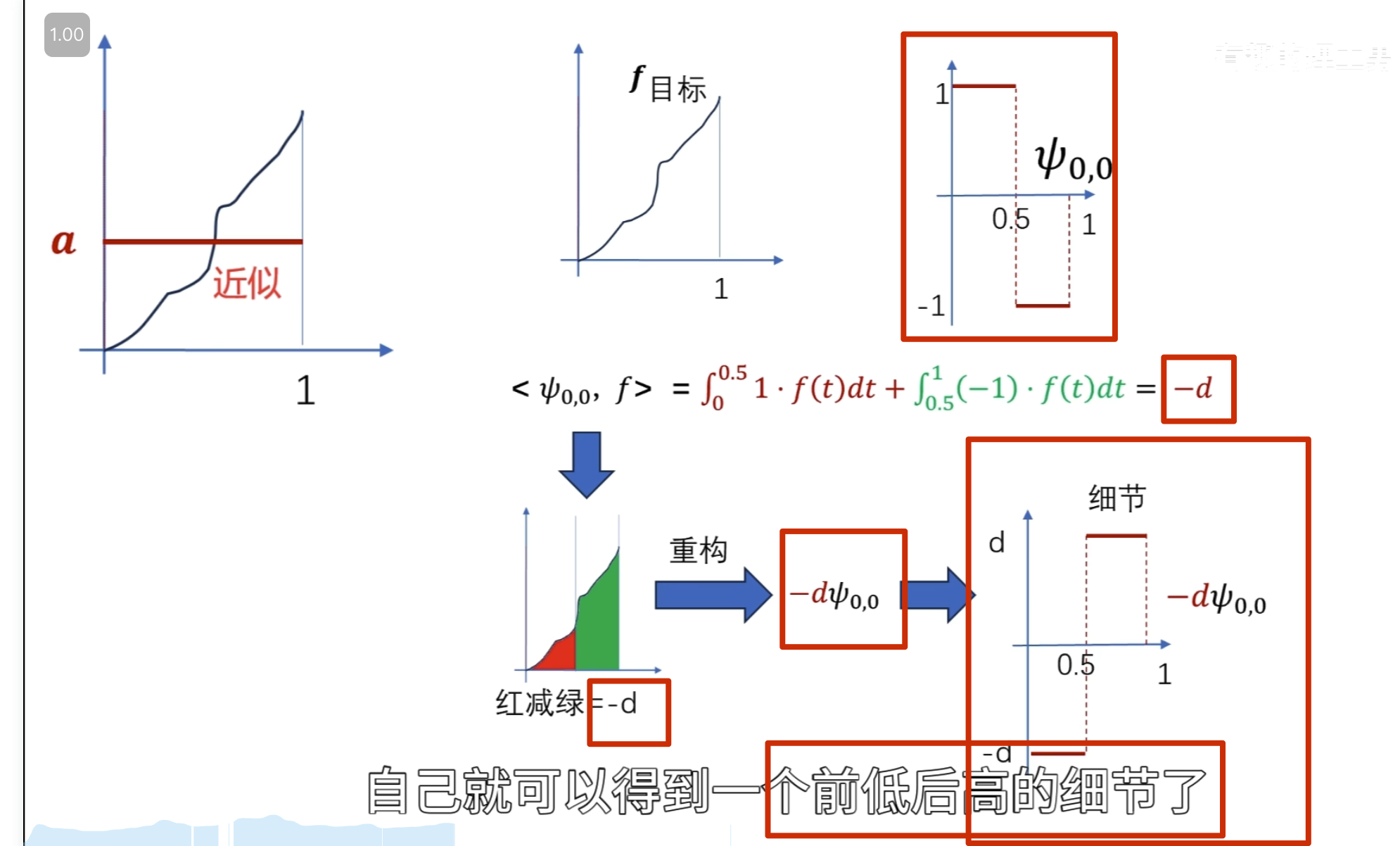












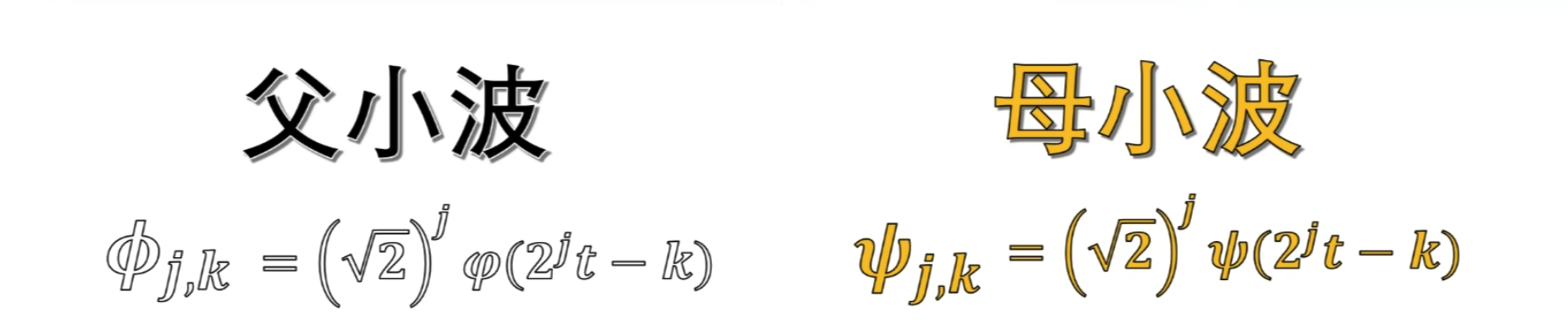
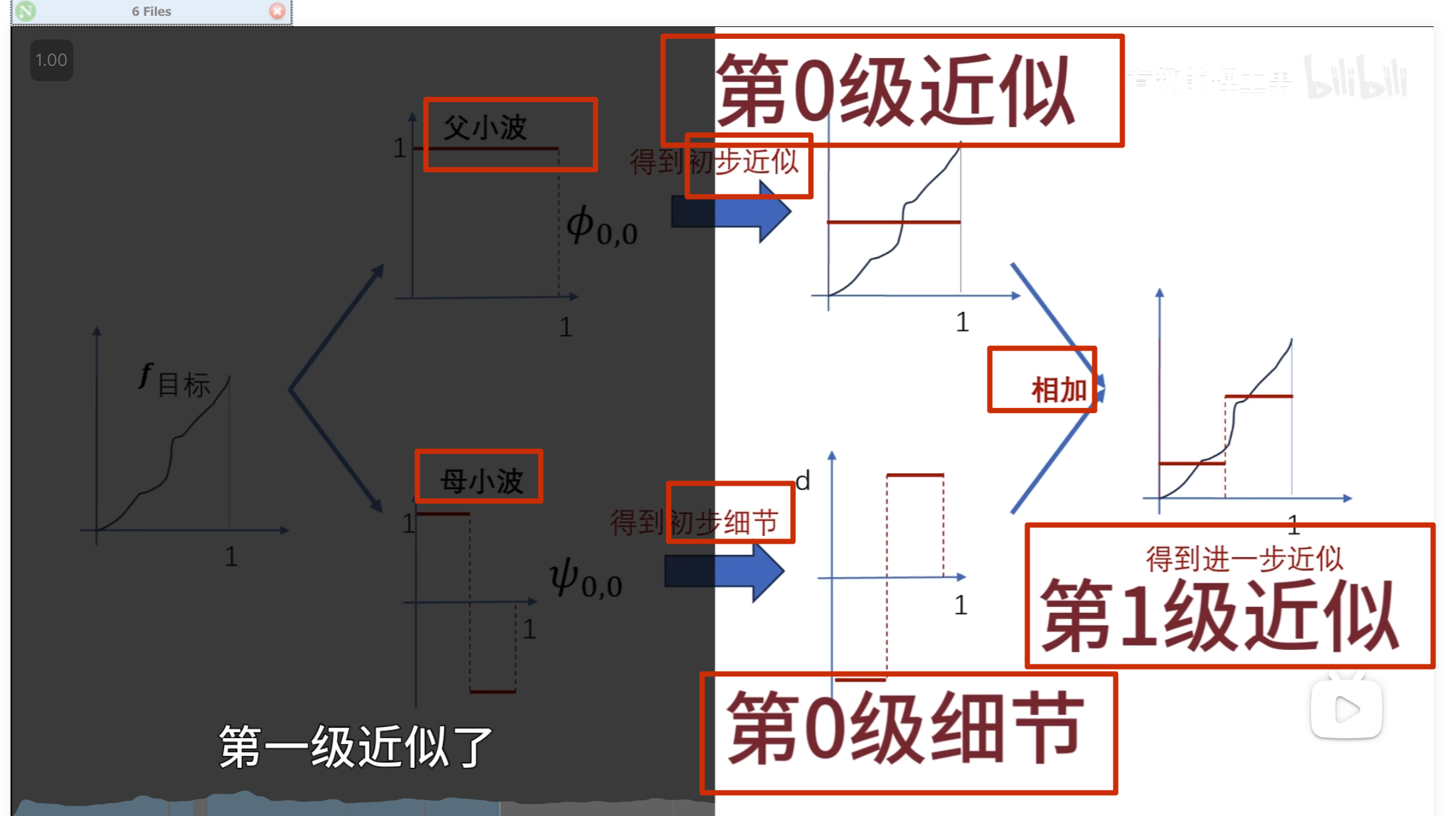


不用第三种方法,原因如下:






可以得到
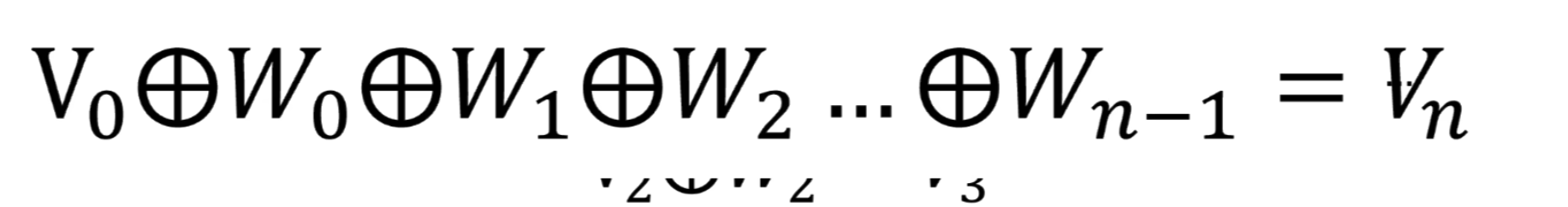
这里按第三种方法其实并没有更快 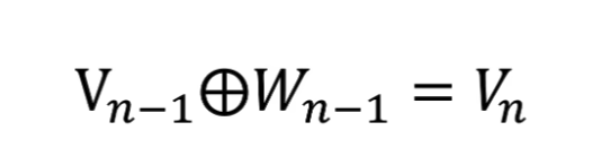





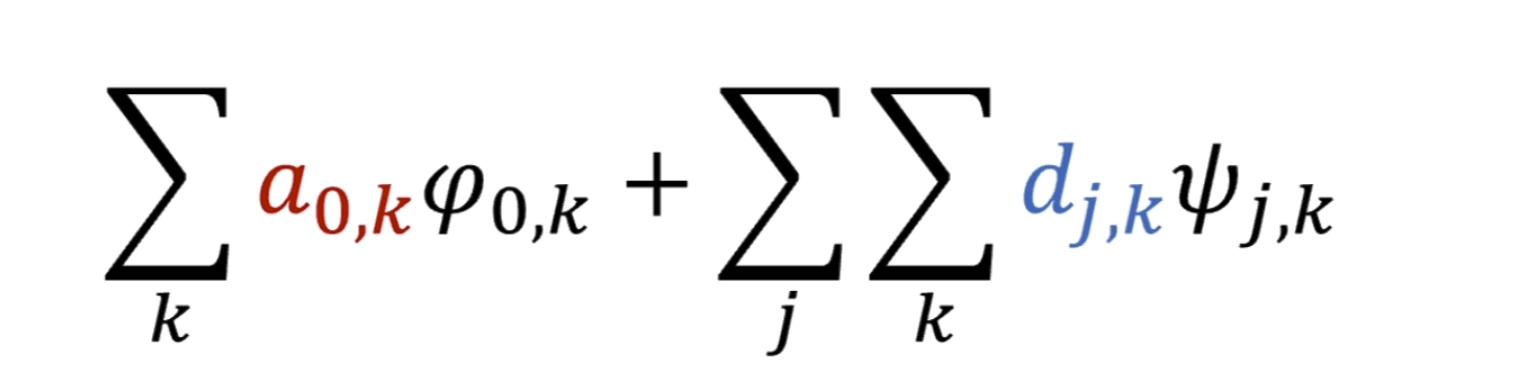






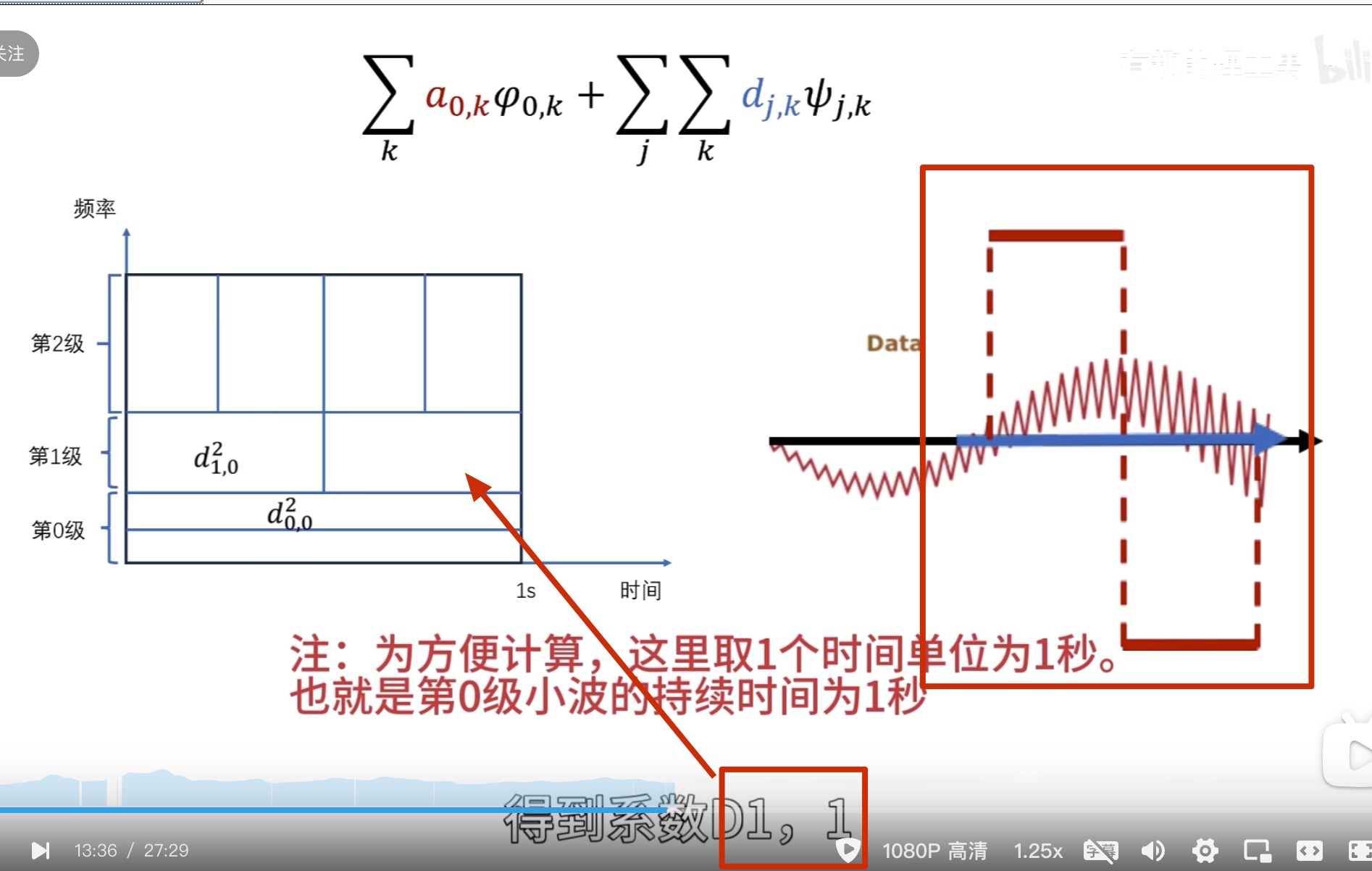
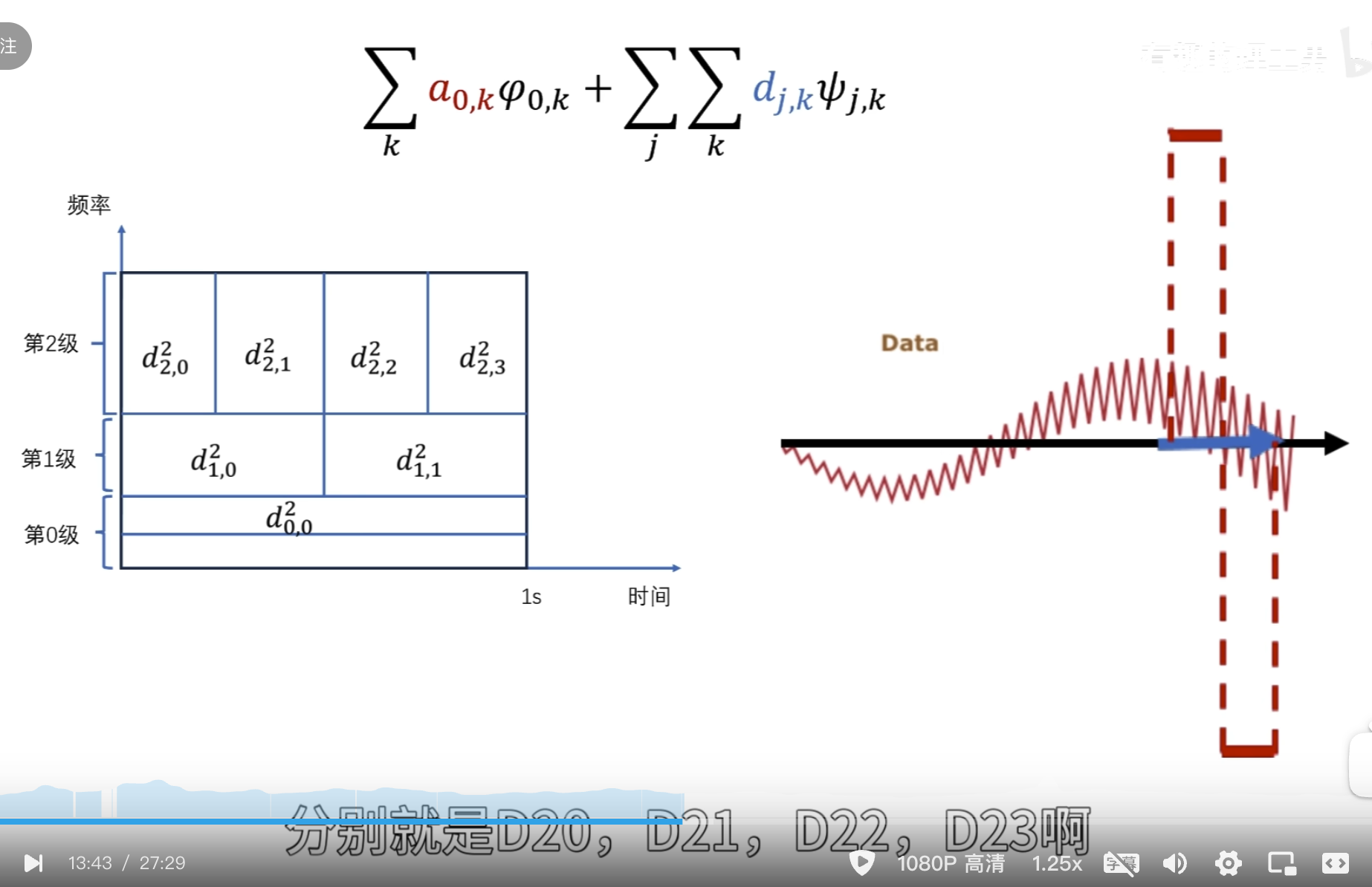
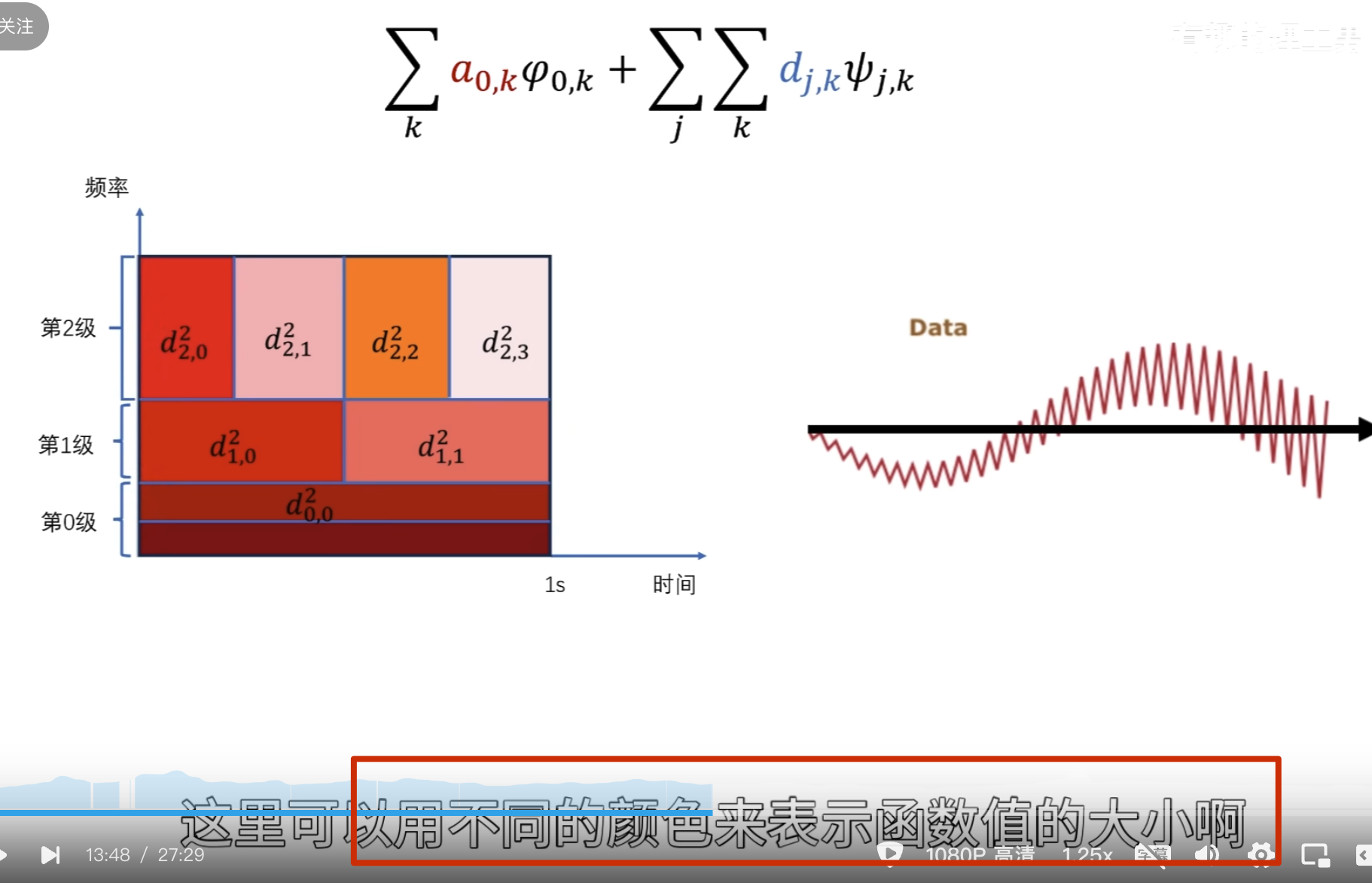
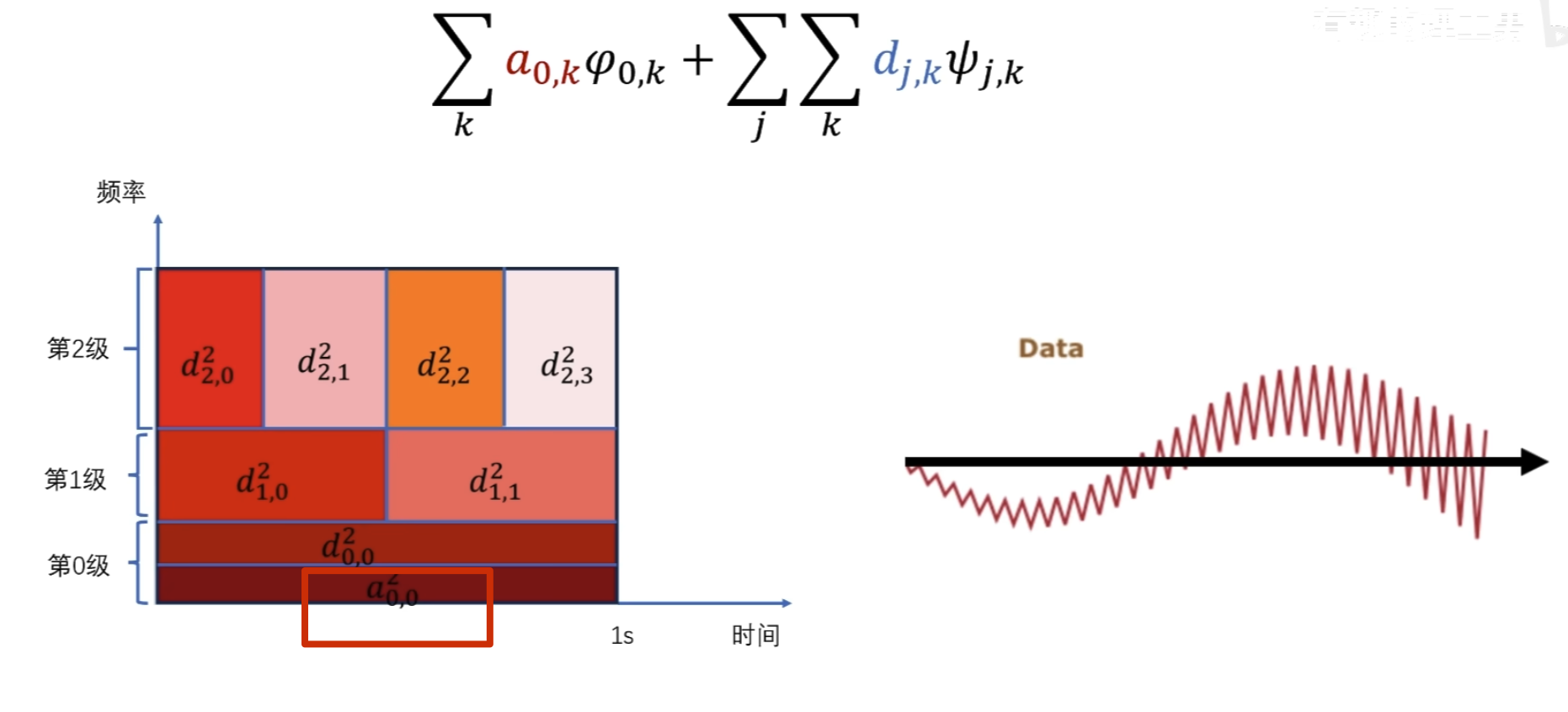
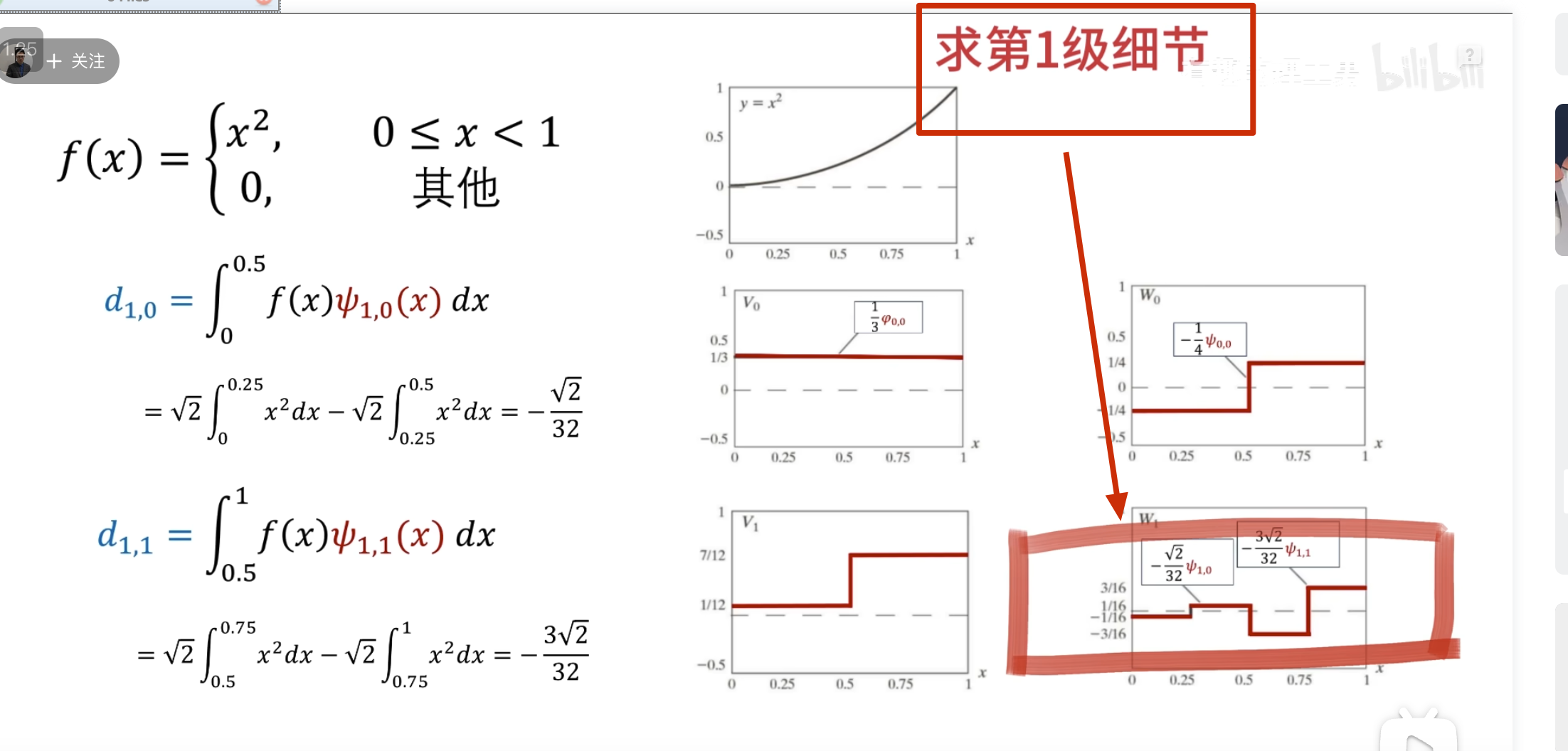
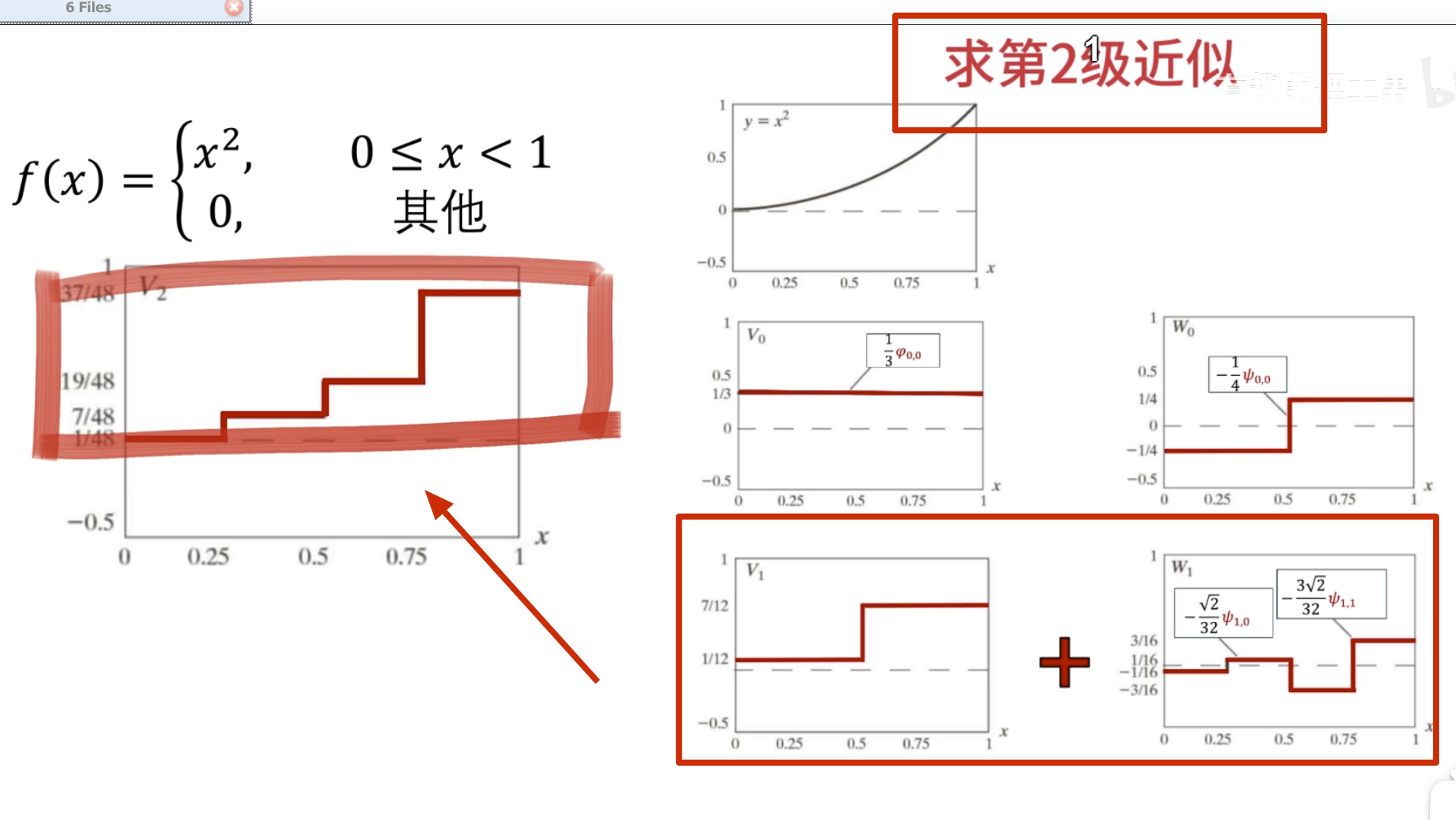
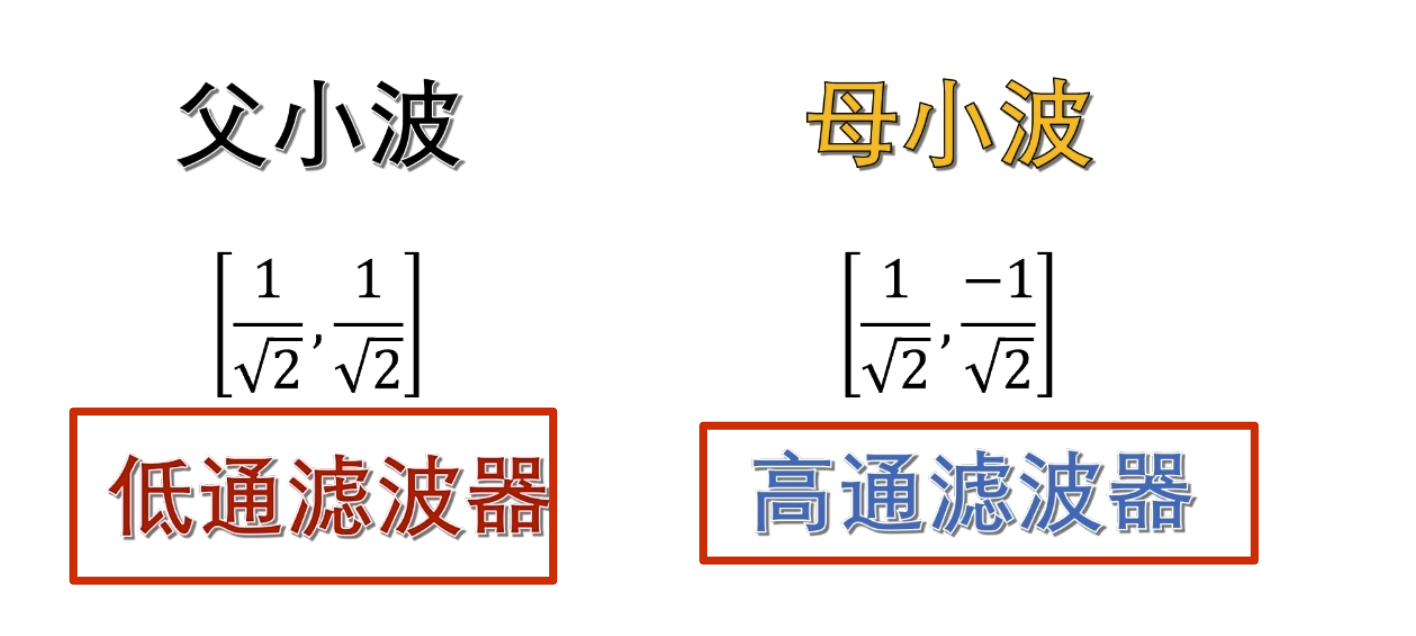
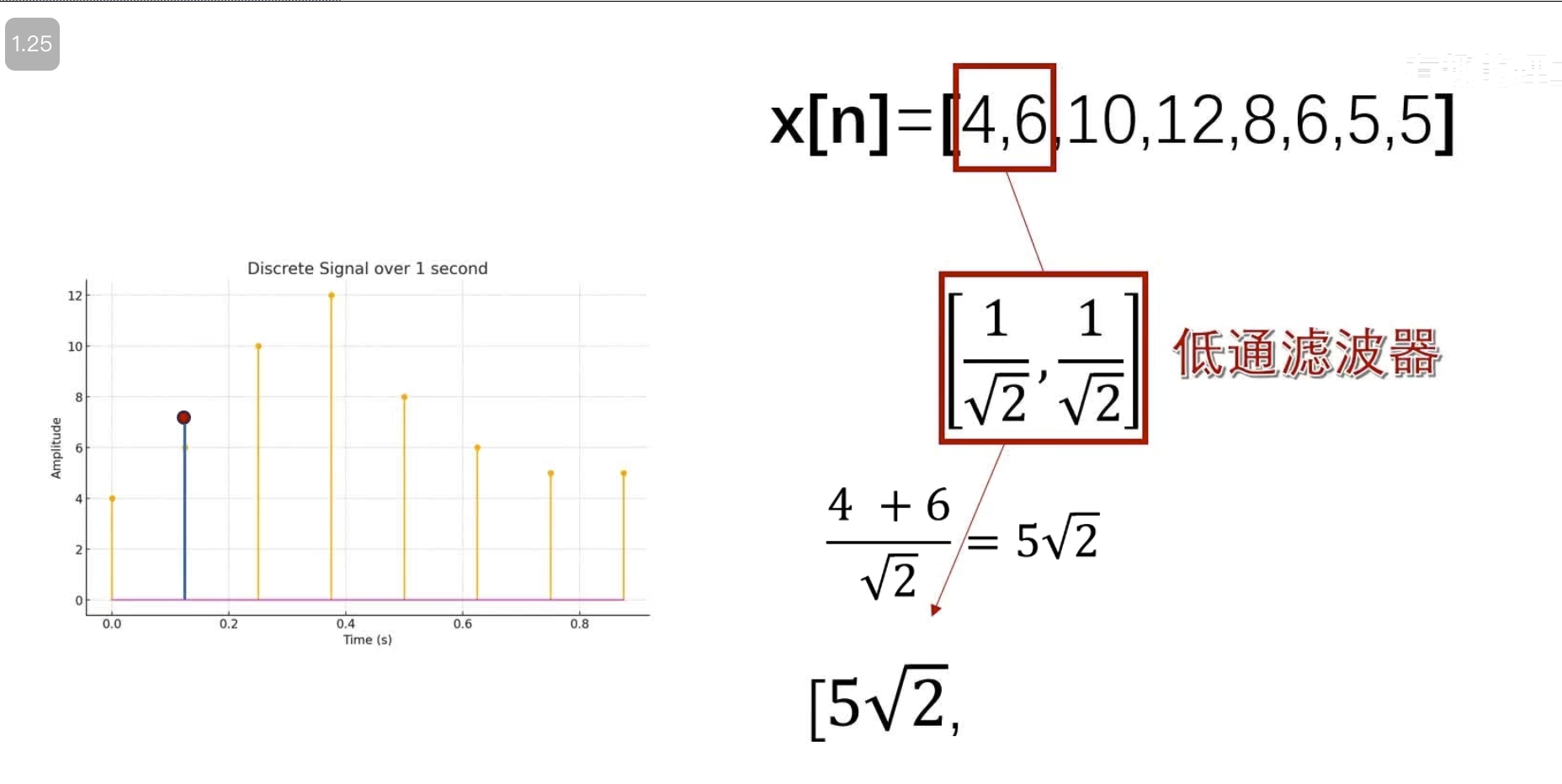
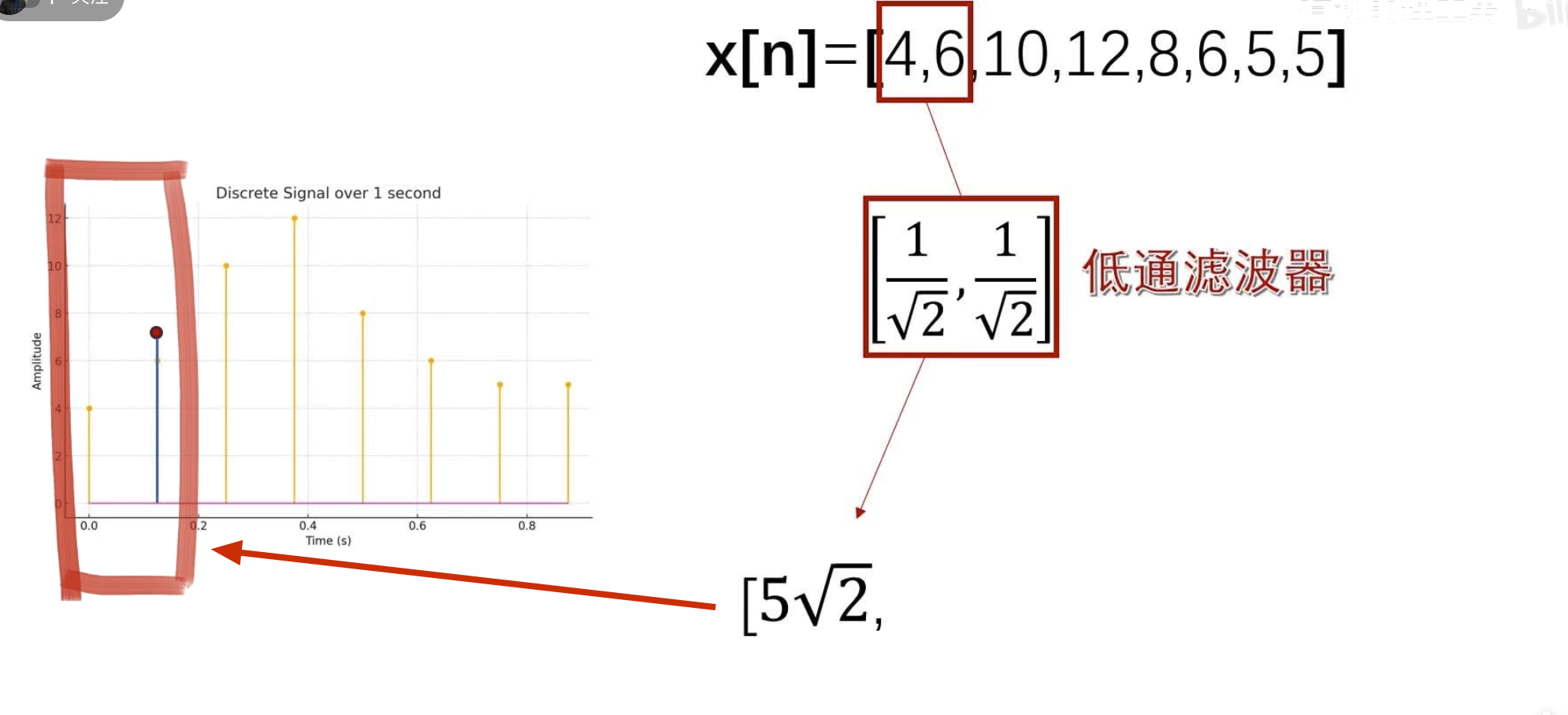
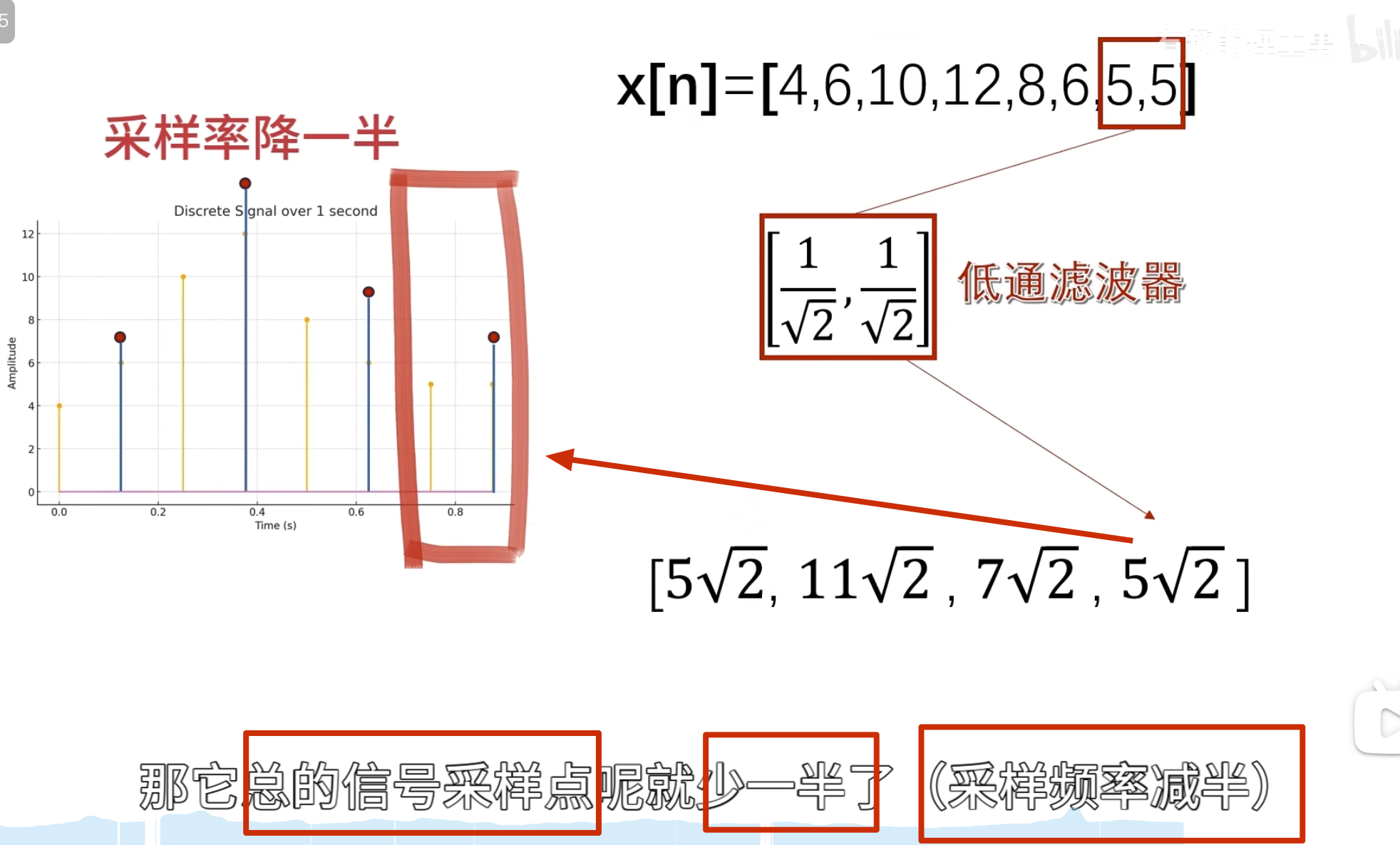
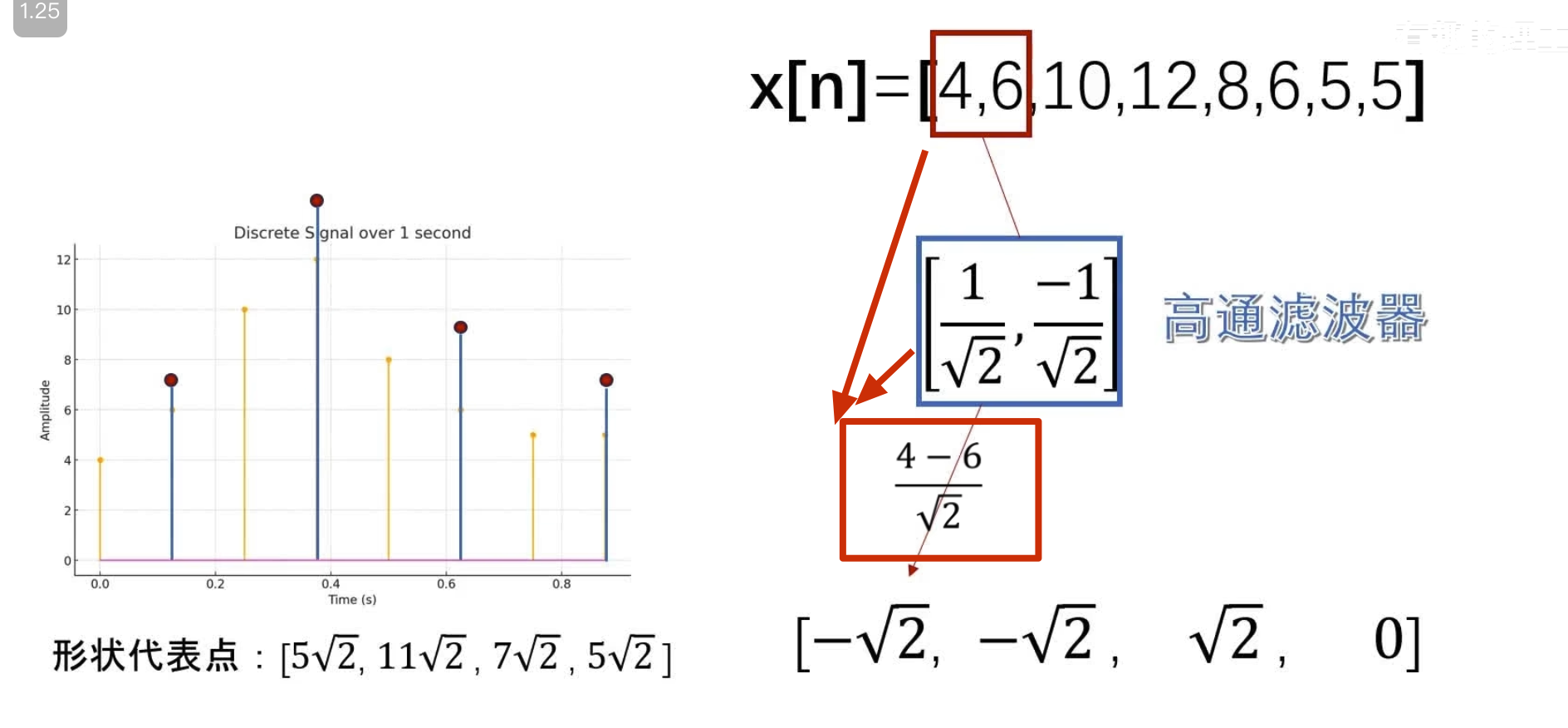
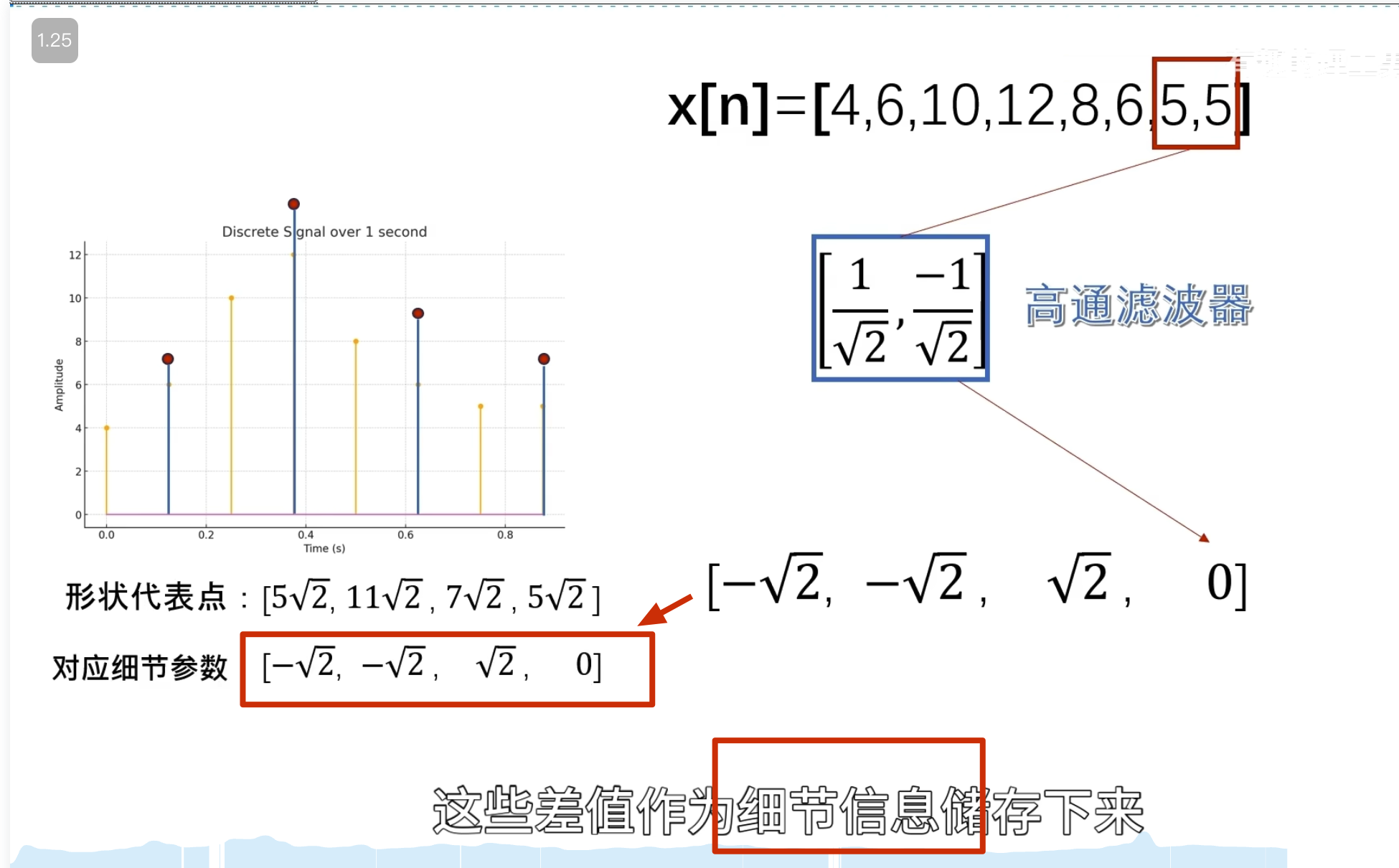
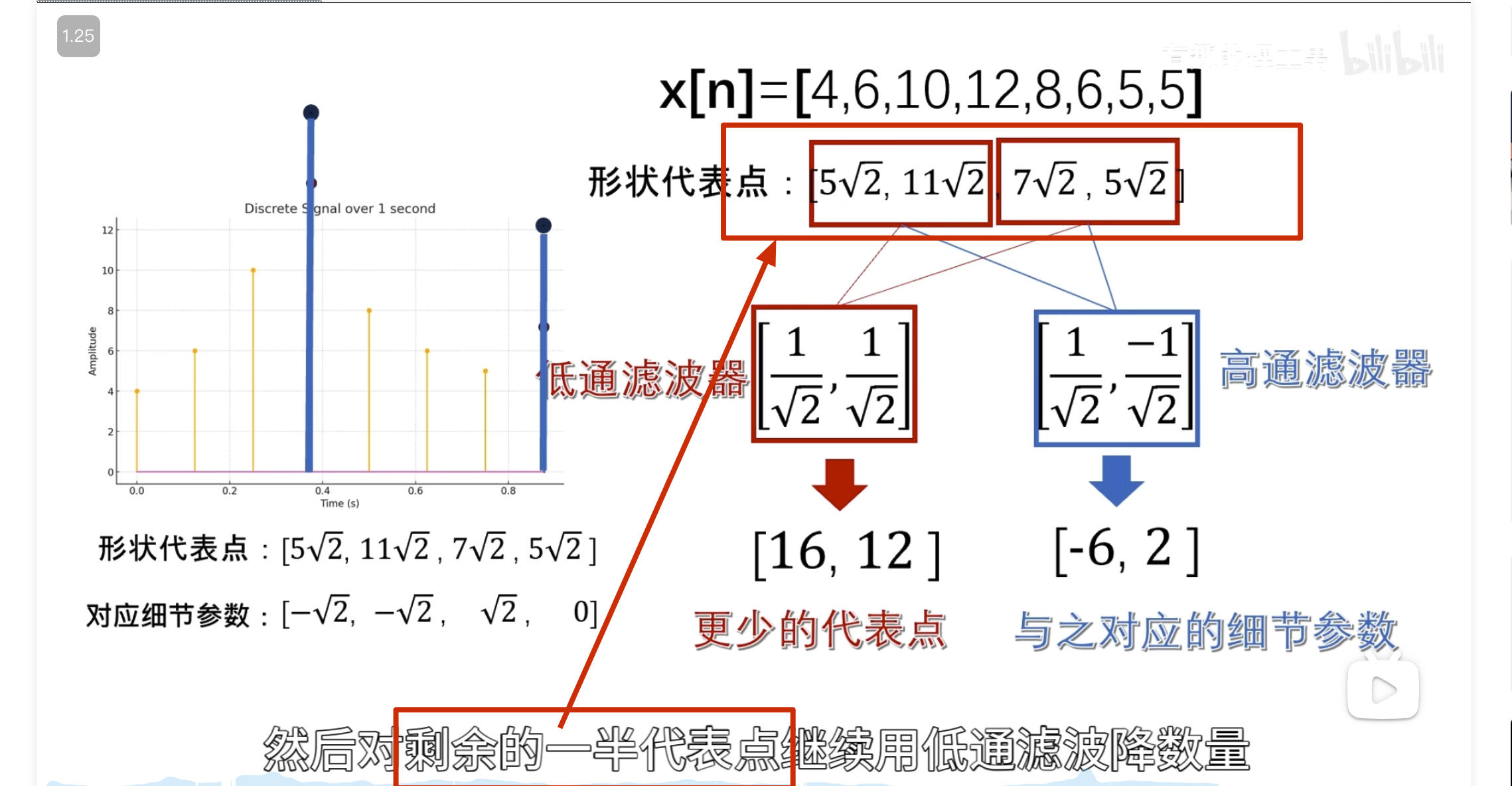
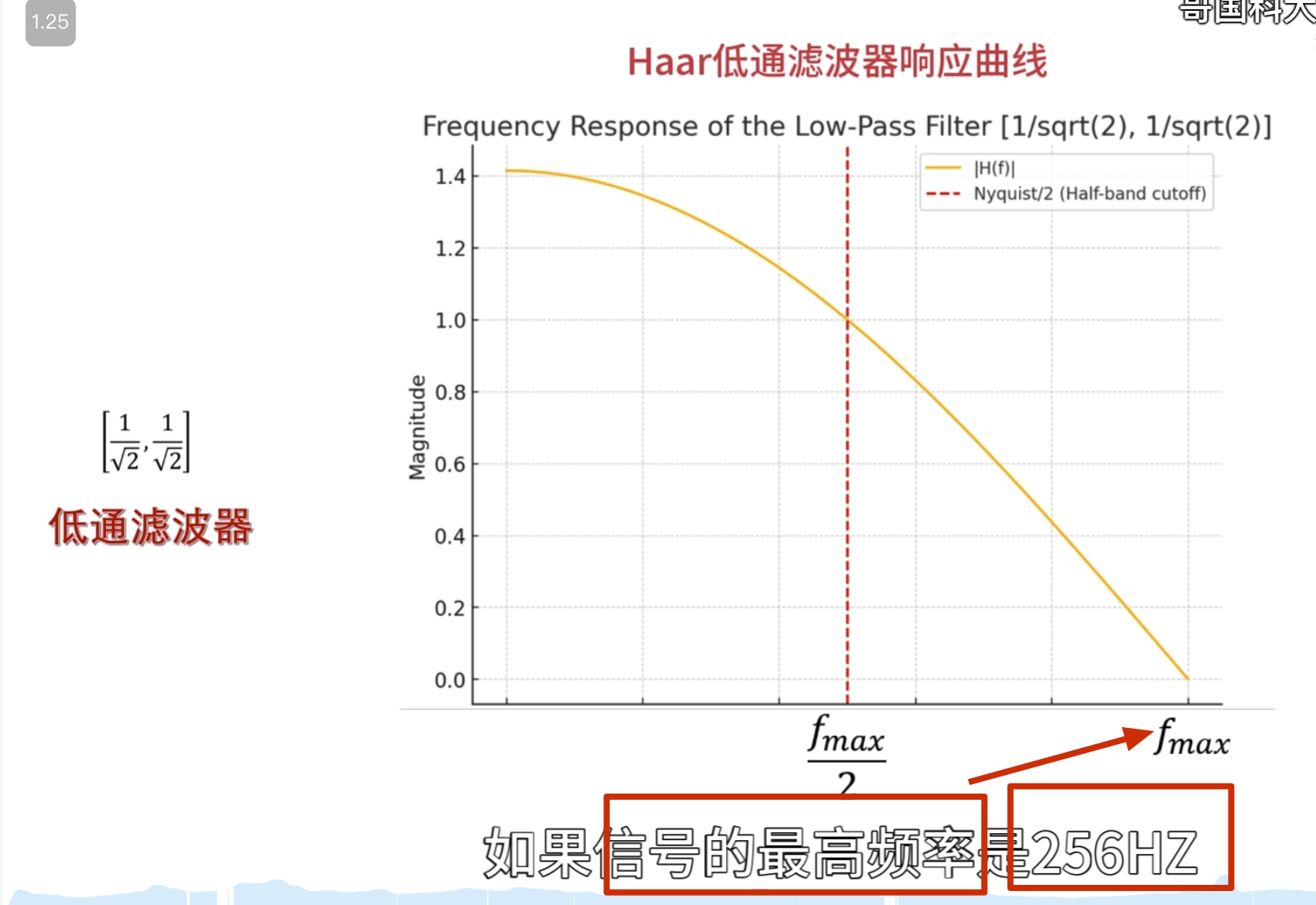
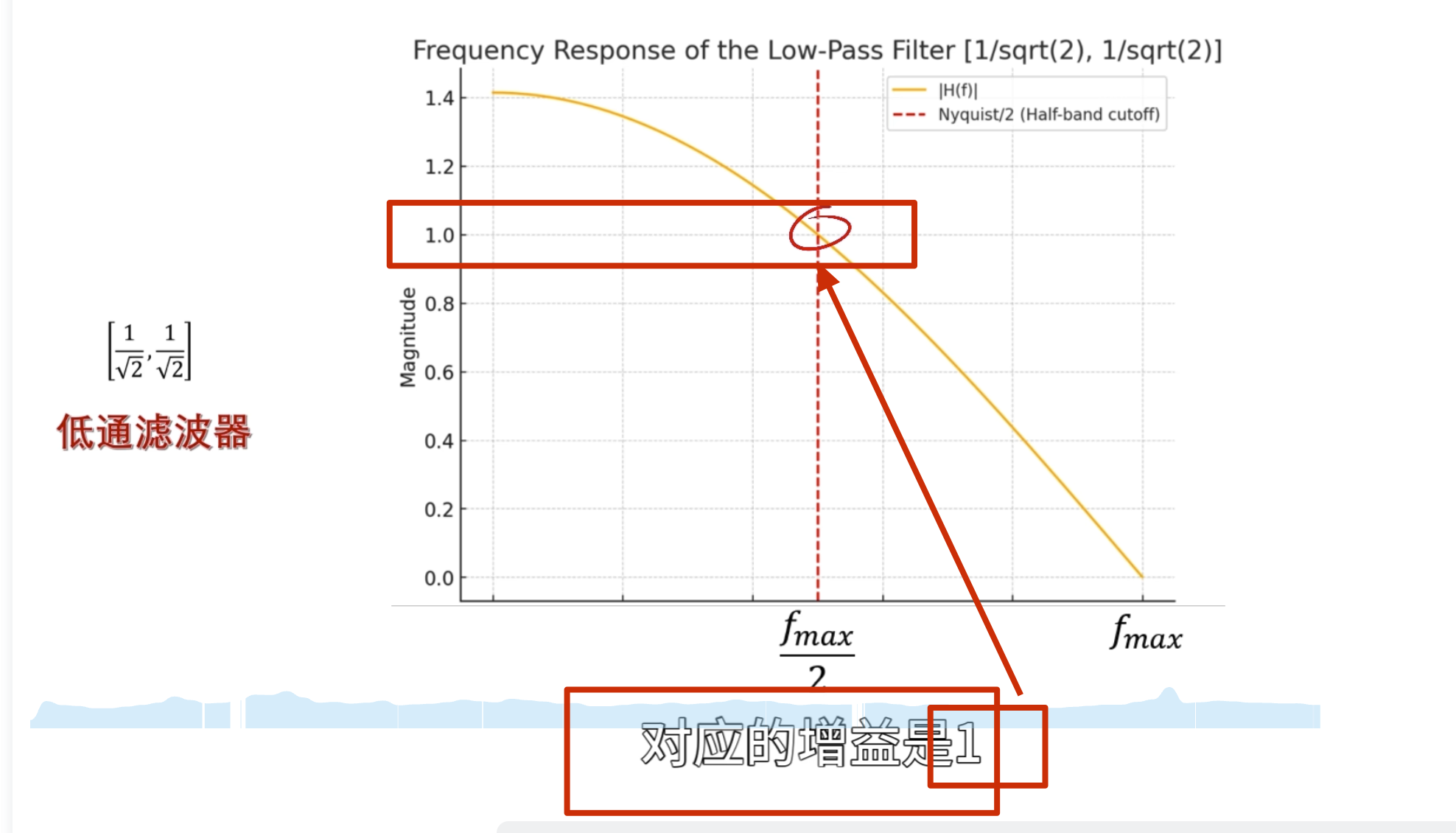
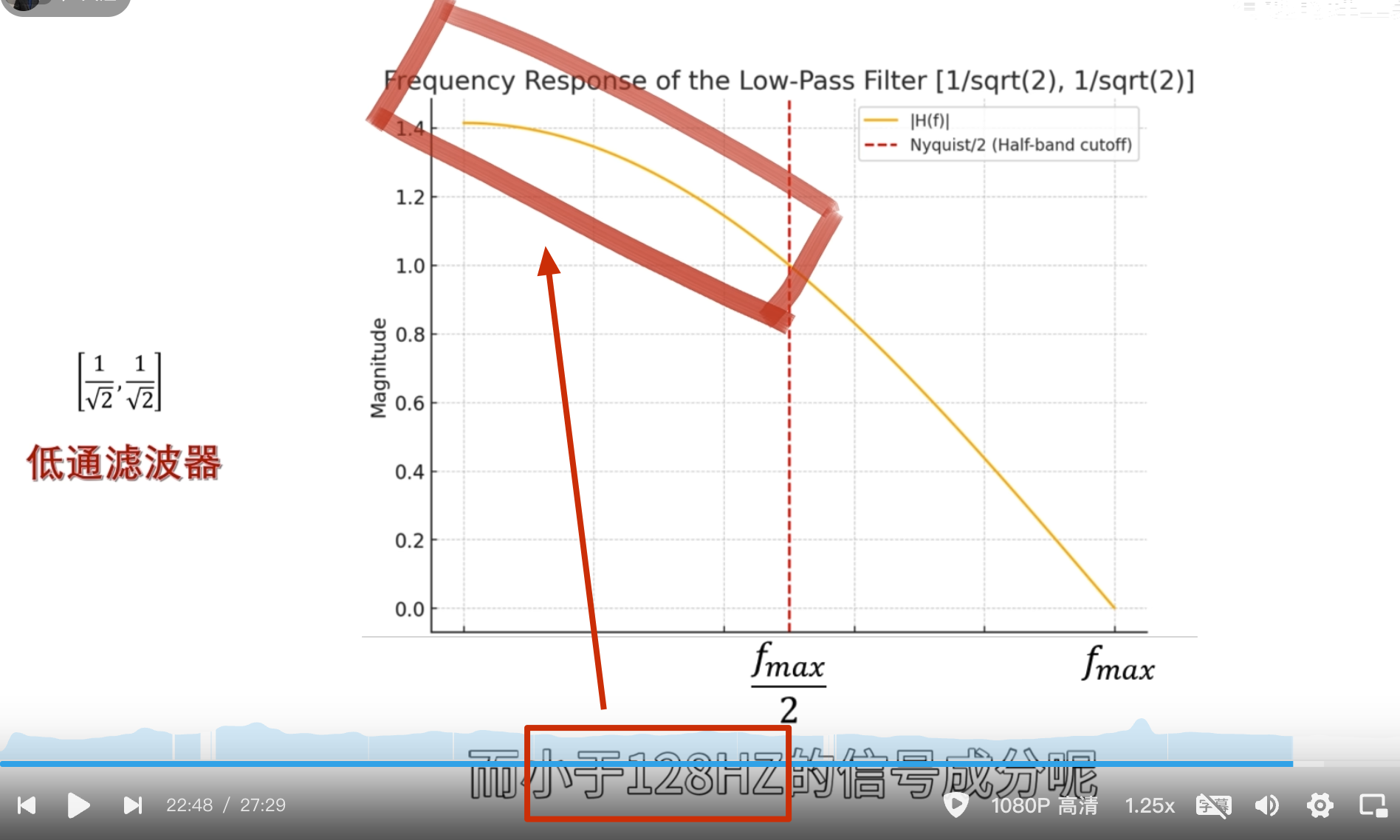
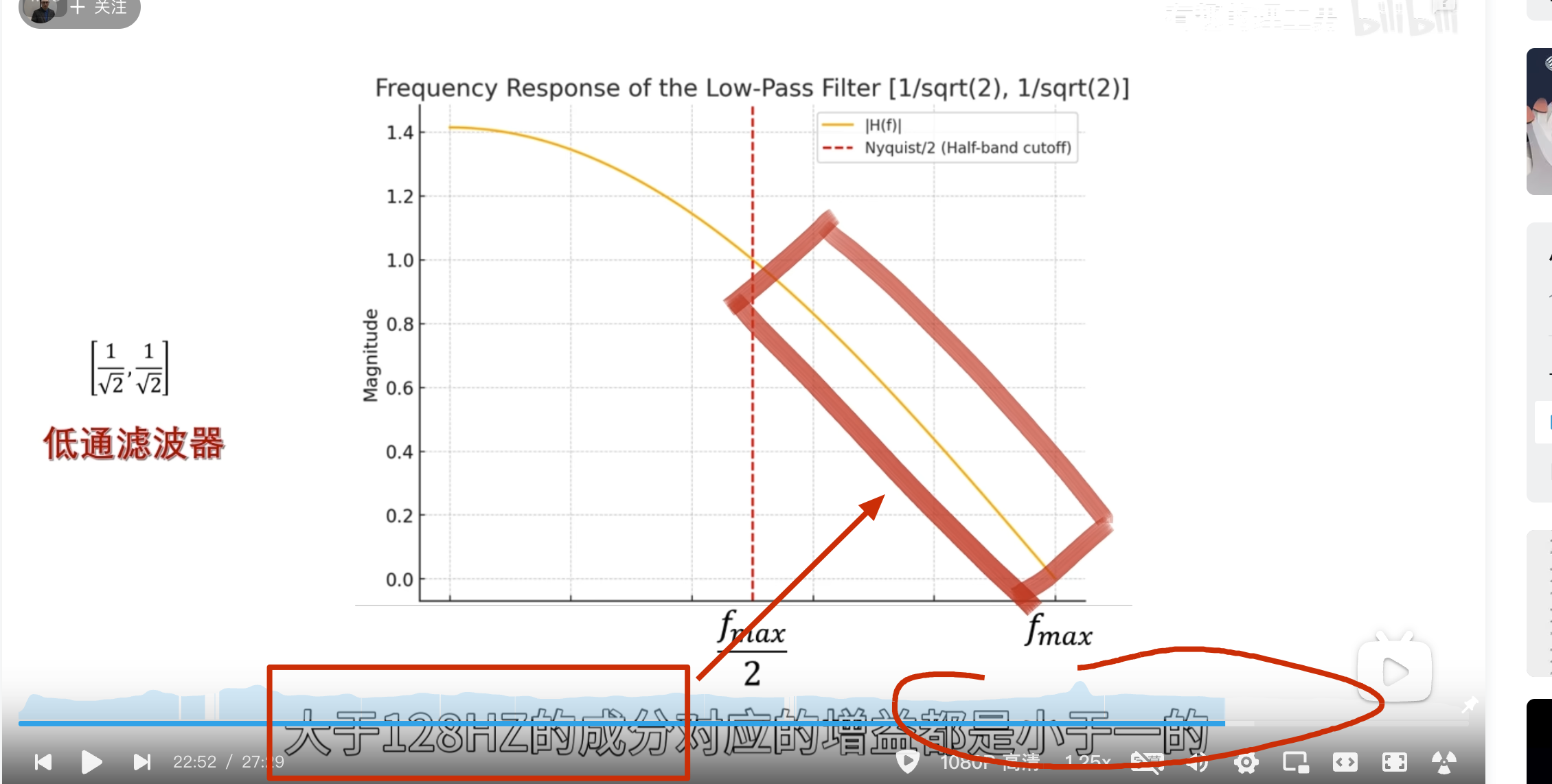
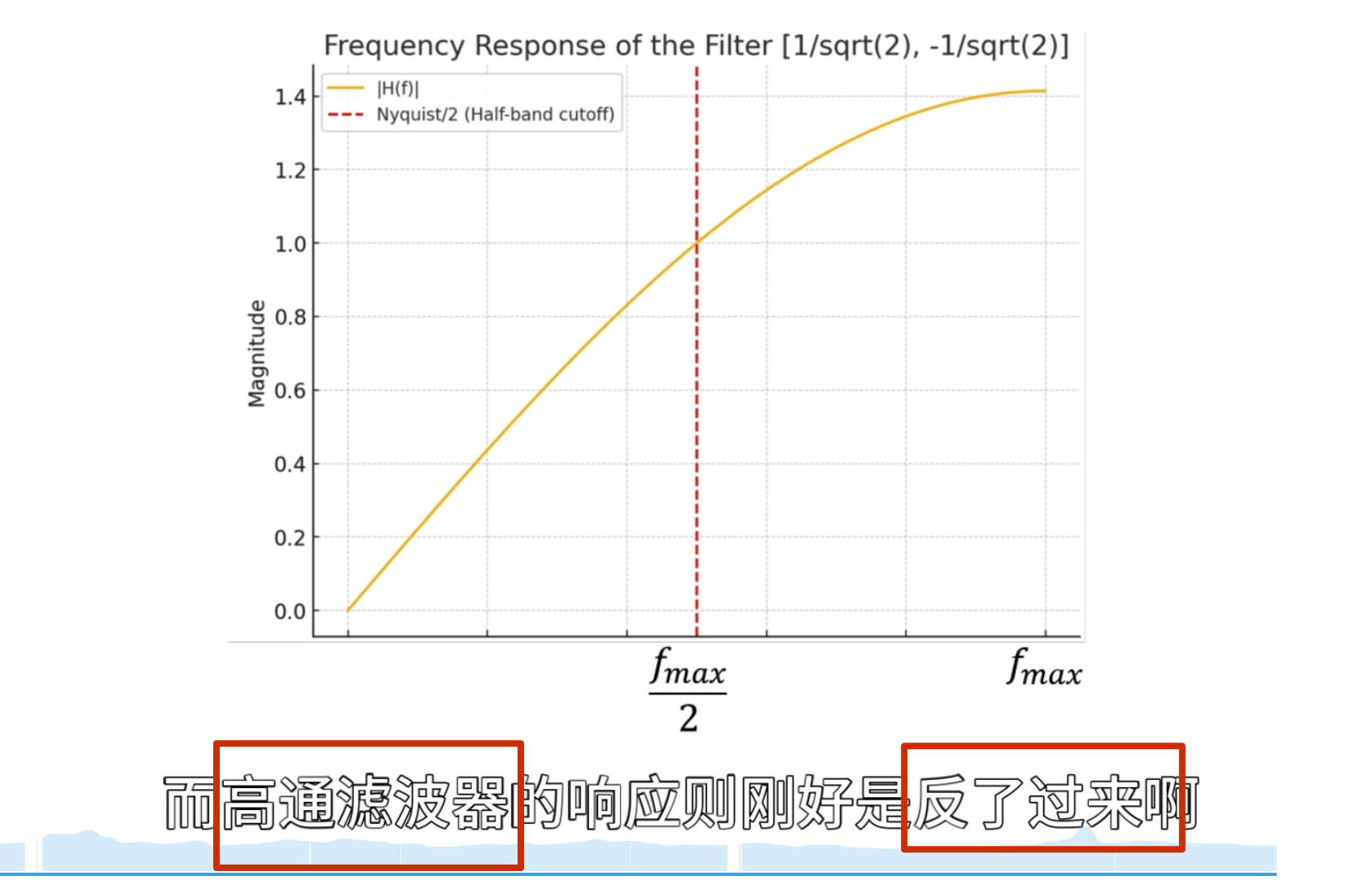
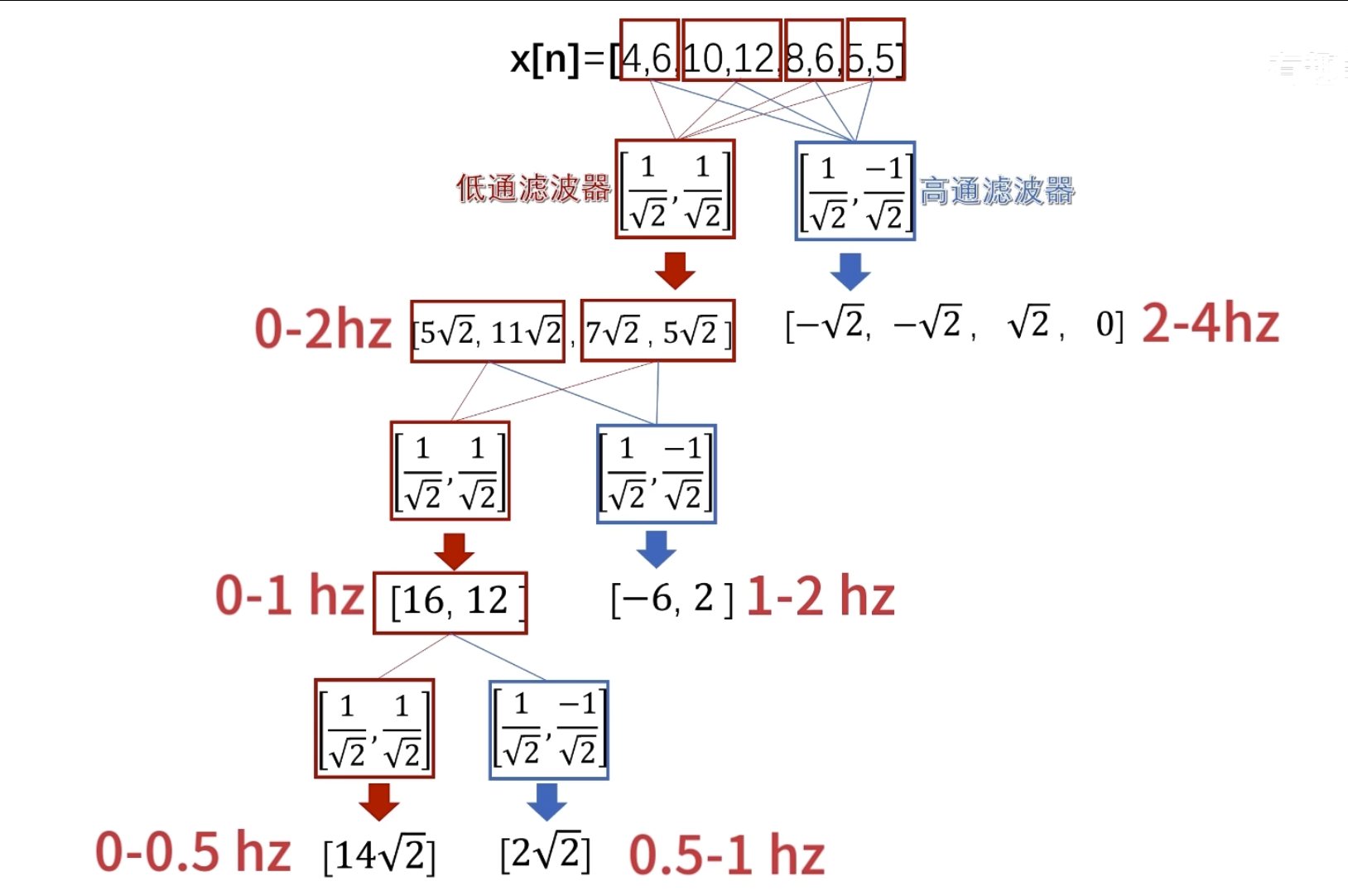
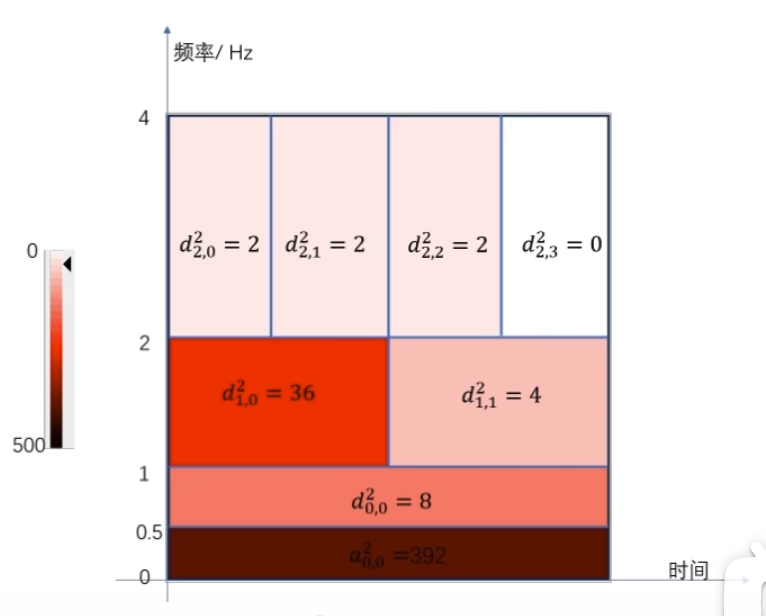
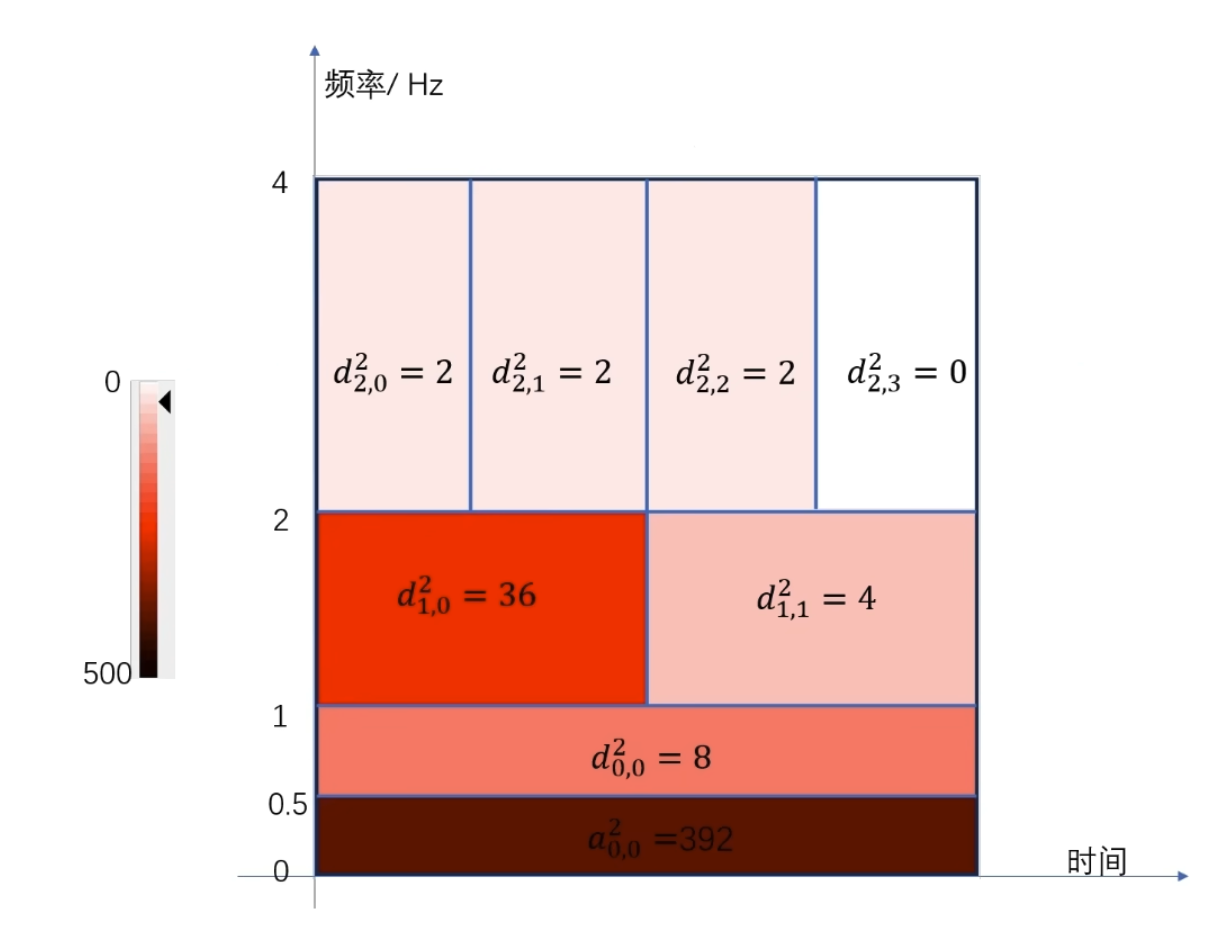
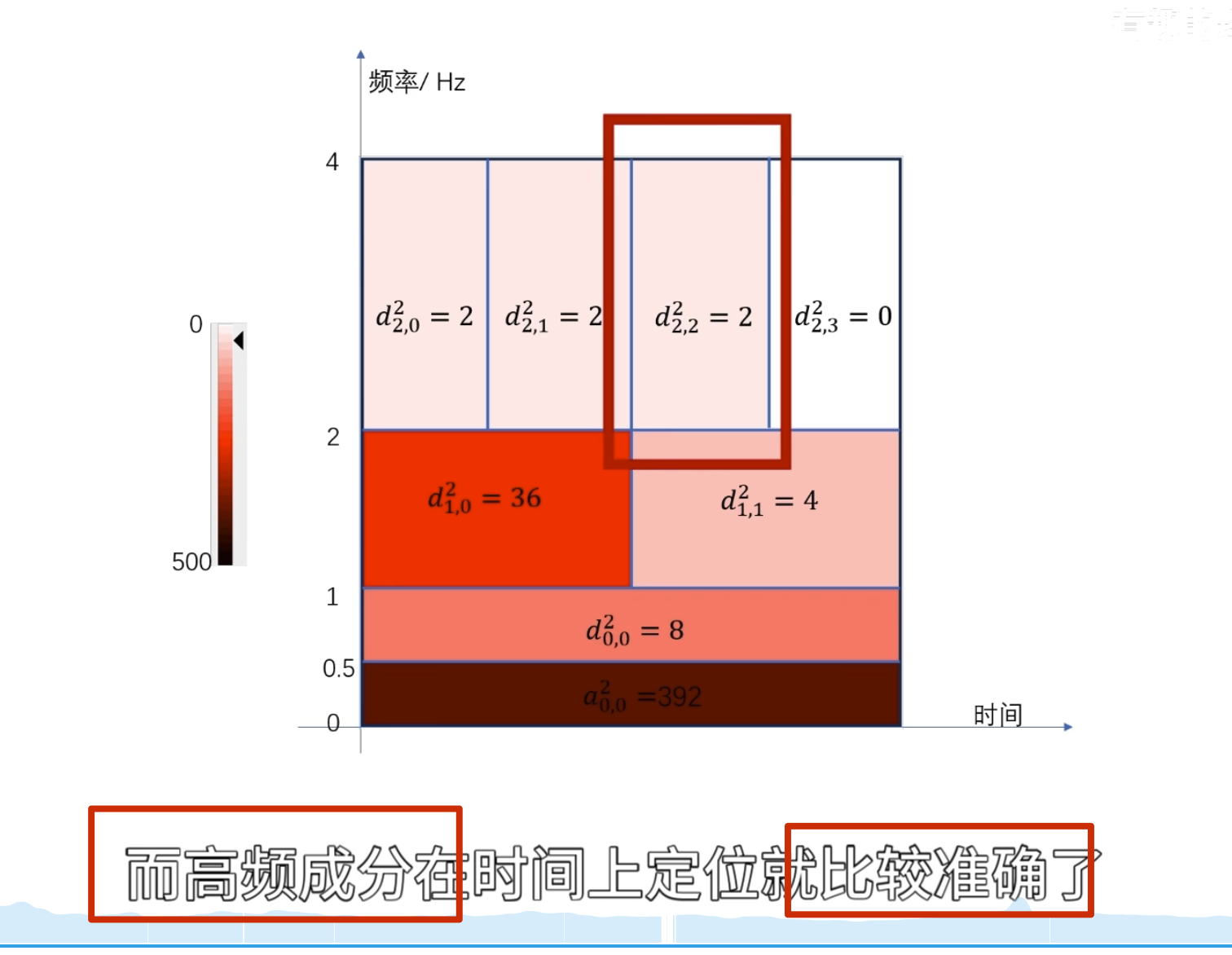
下面的没啥用,但是后面高低通滤波的时候要用到
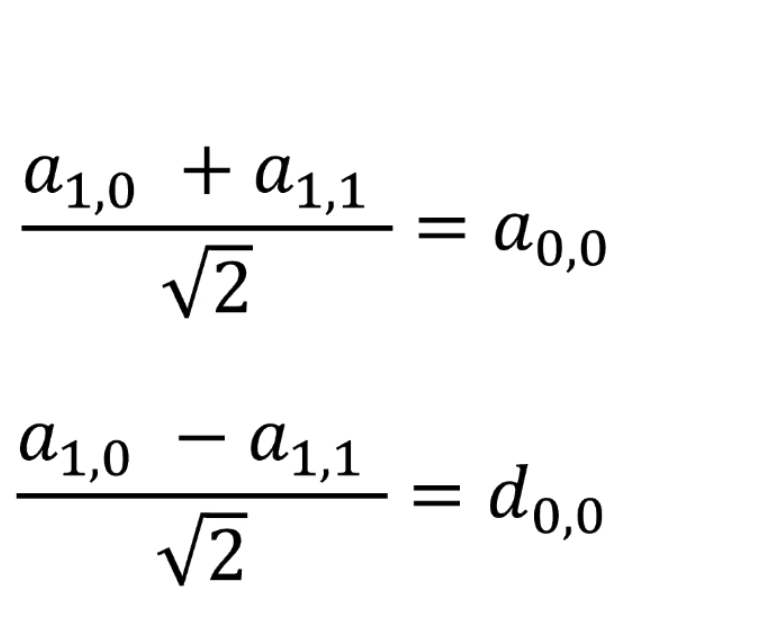


































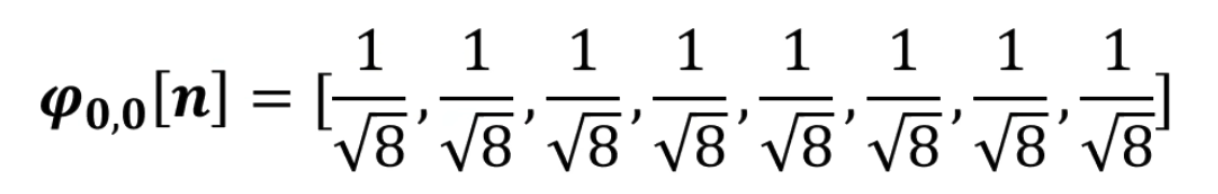

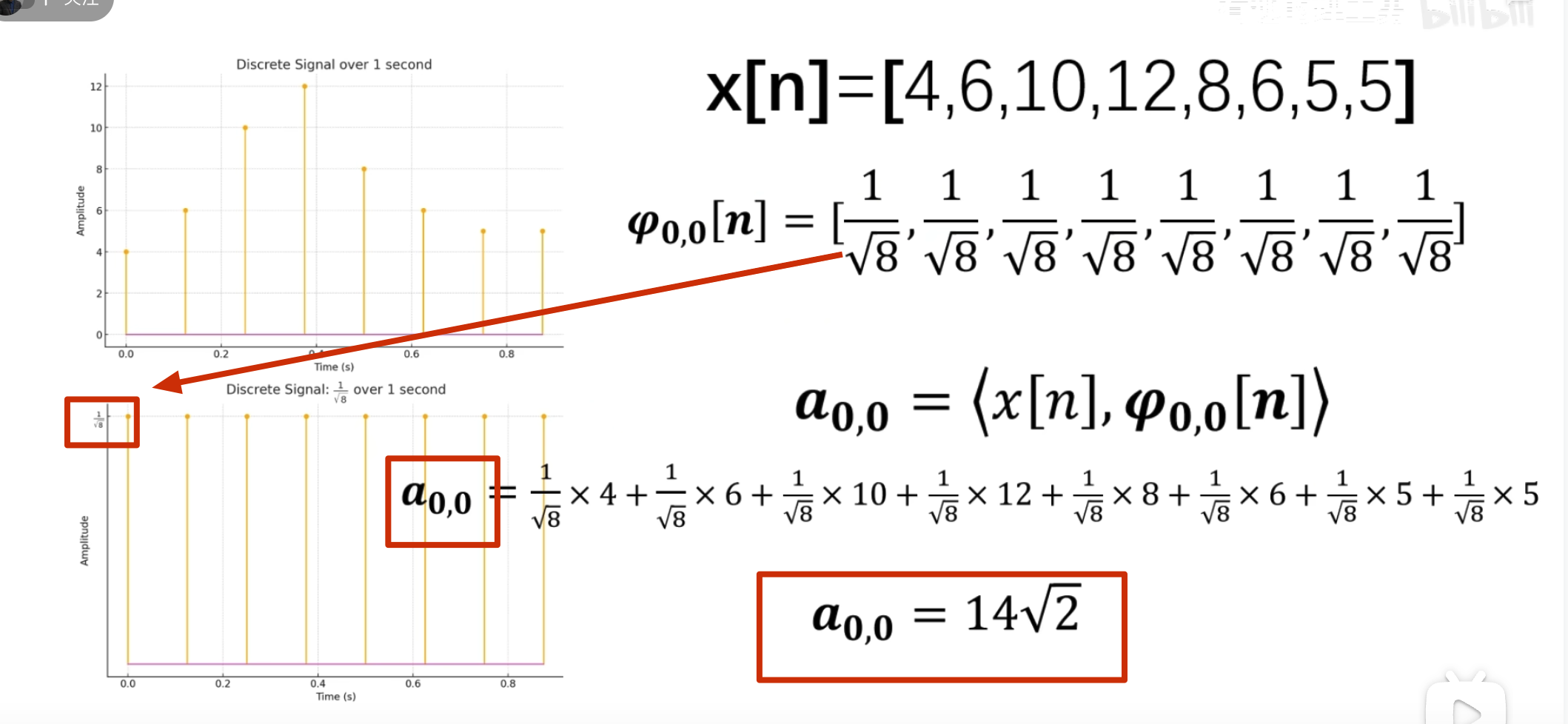
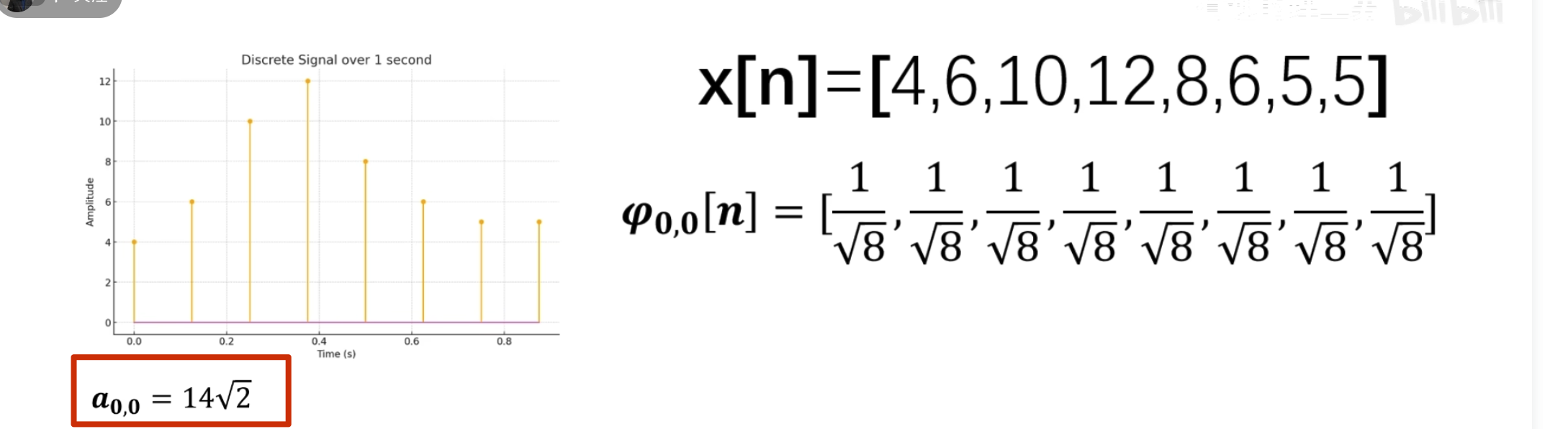

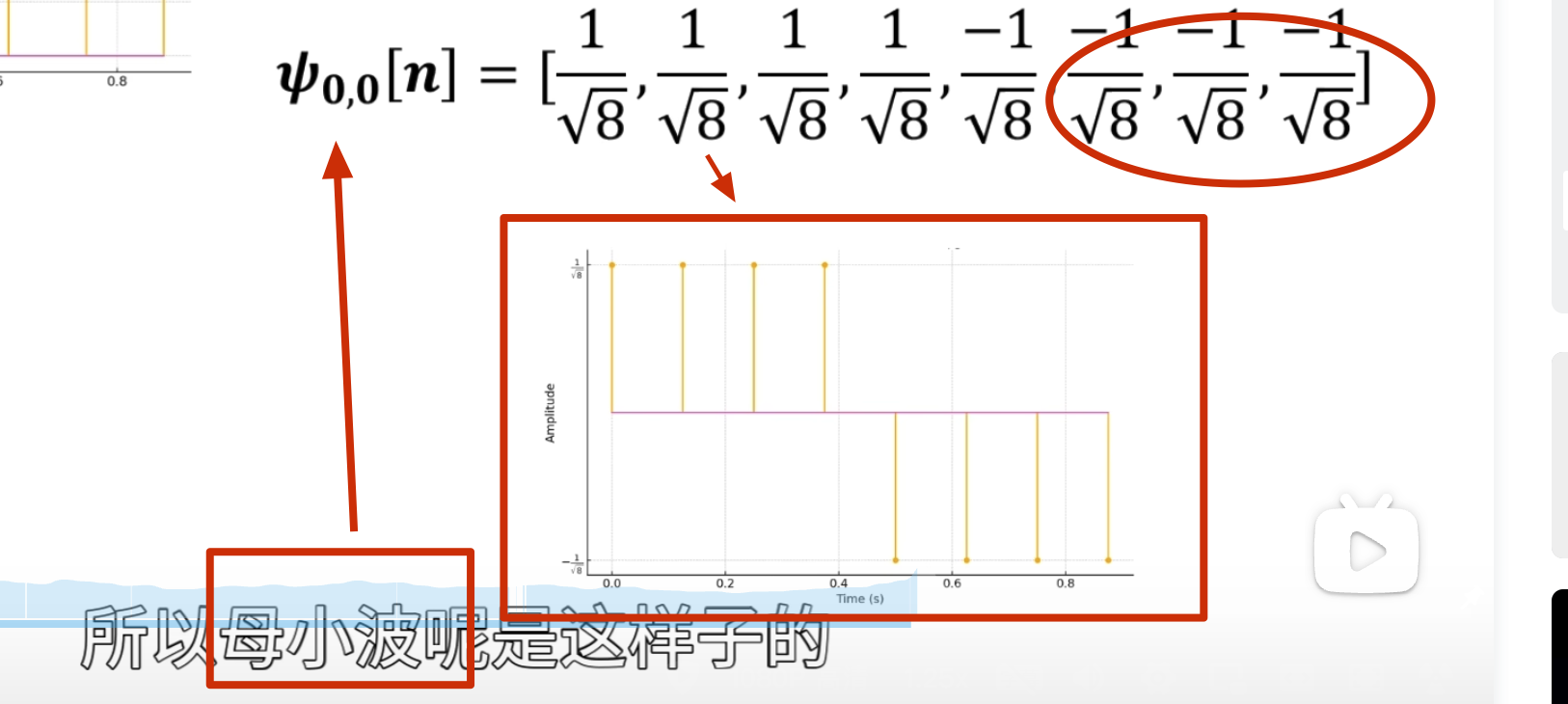
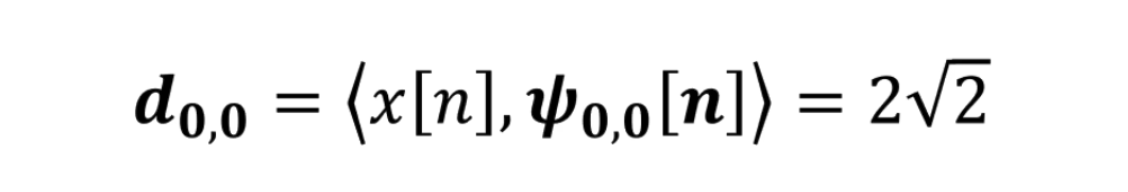


点乘结果
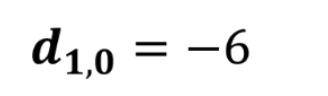
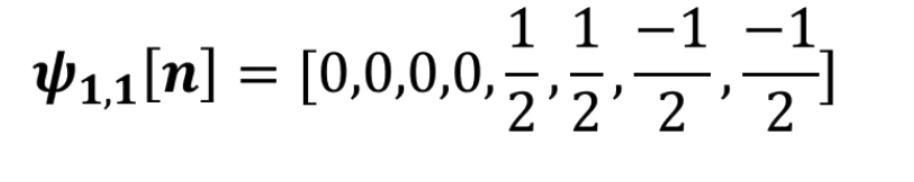
点乘结果
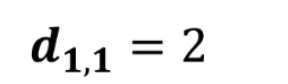
第二级母小波
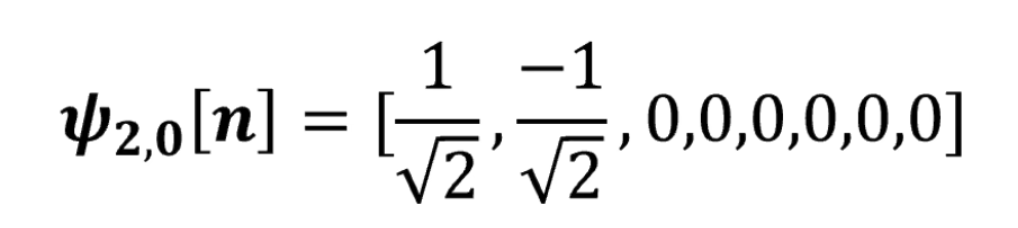

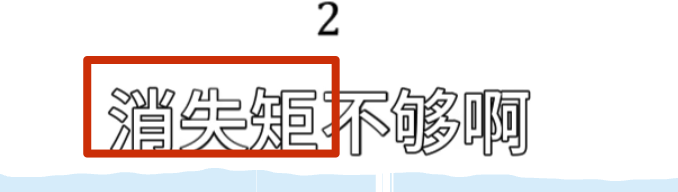
点乘结果
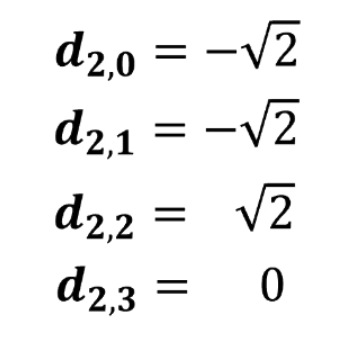
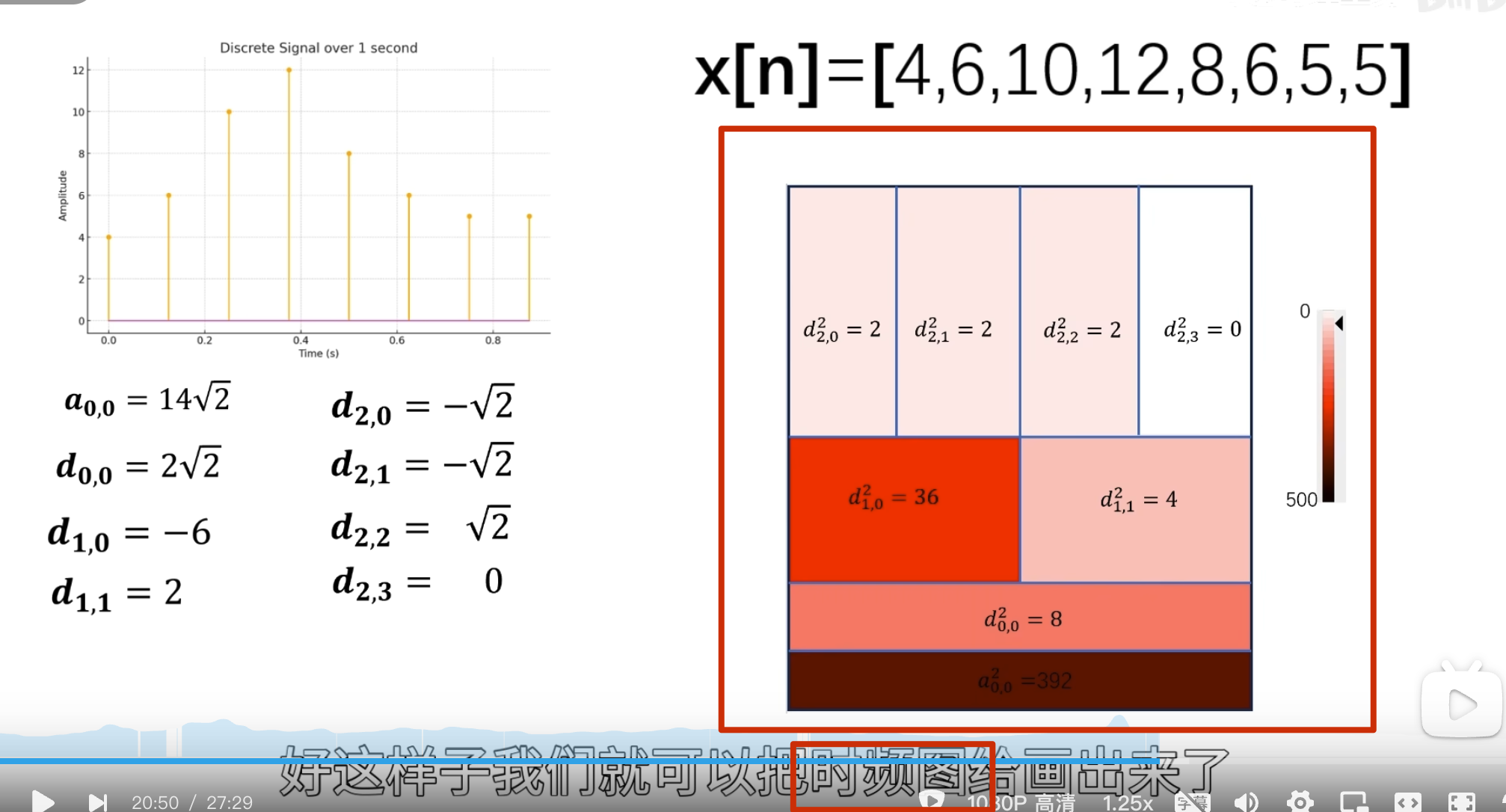


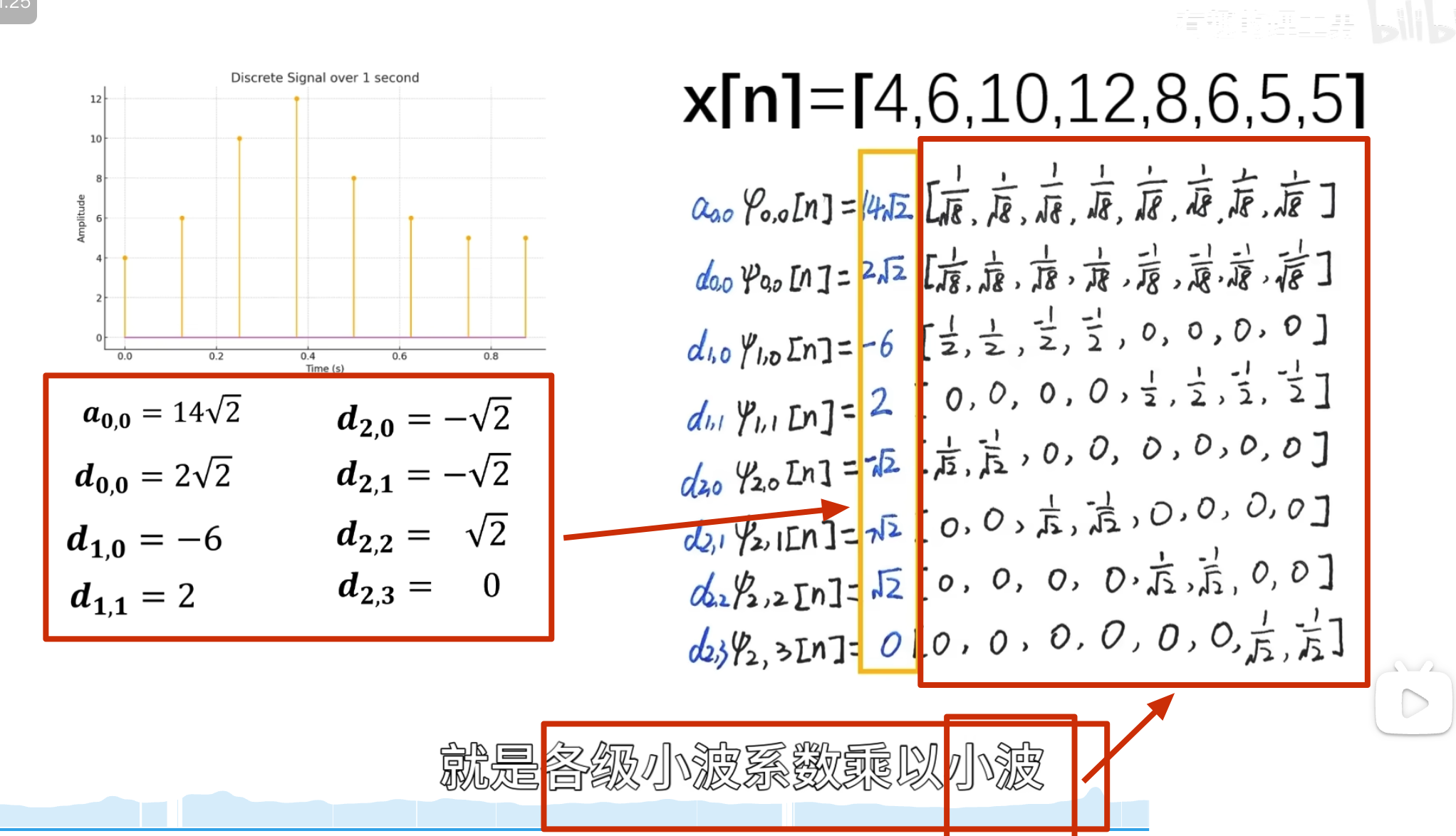

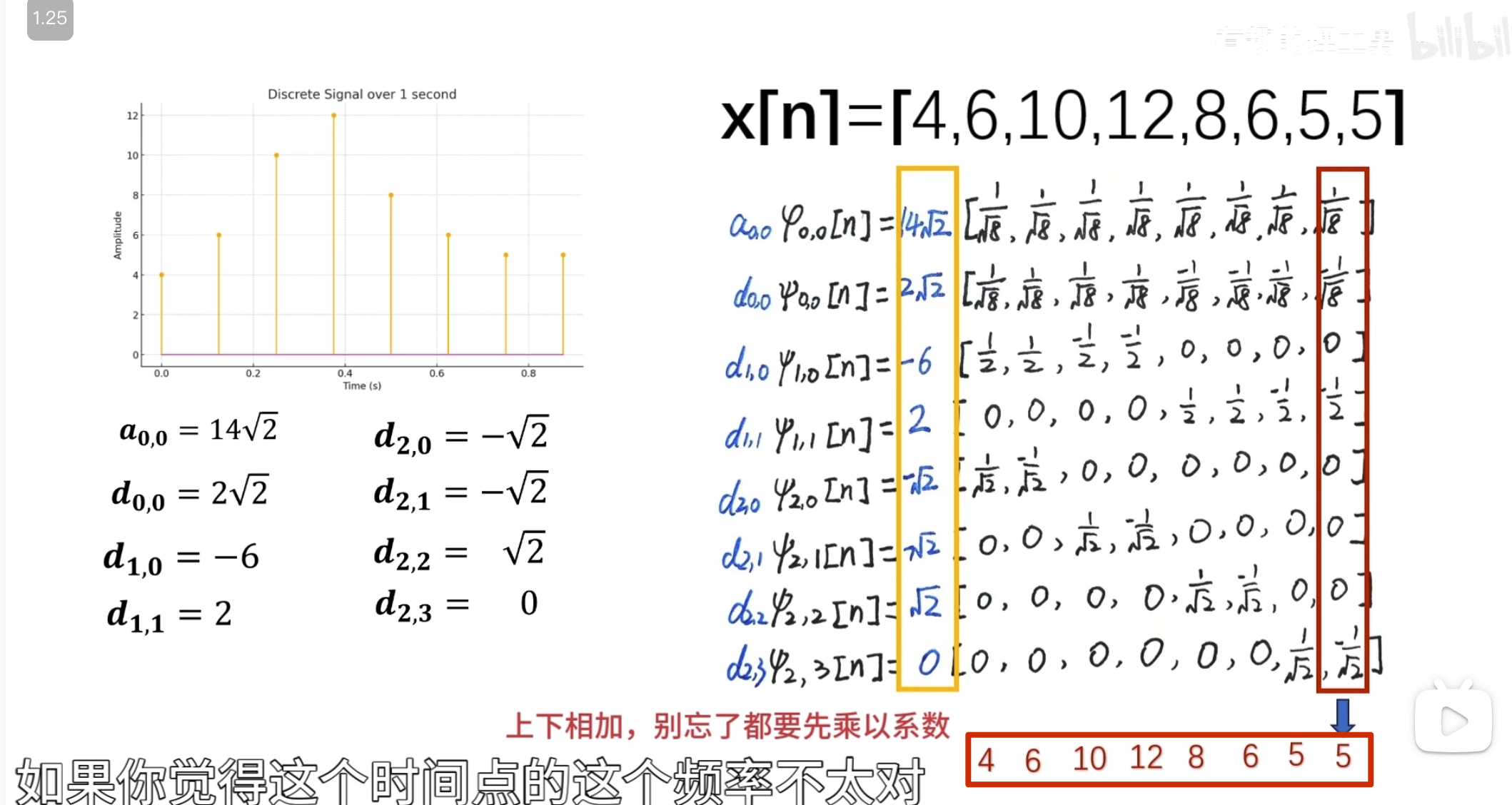
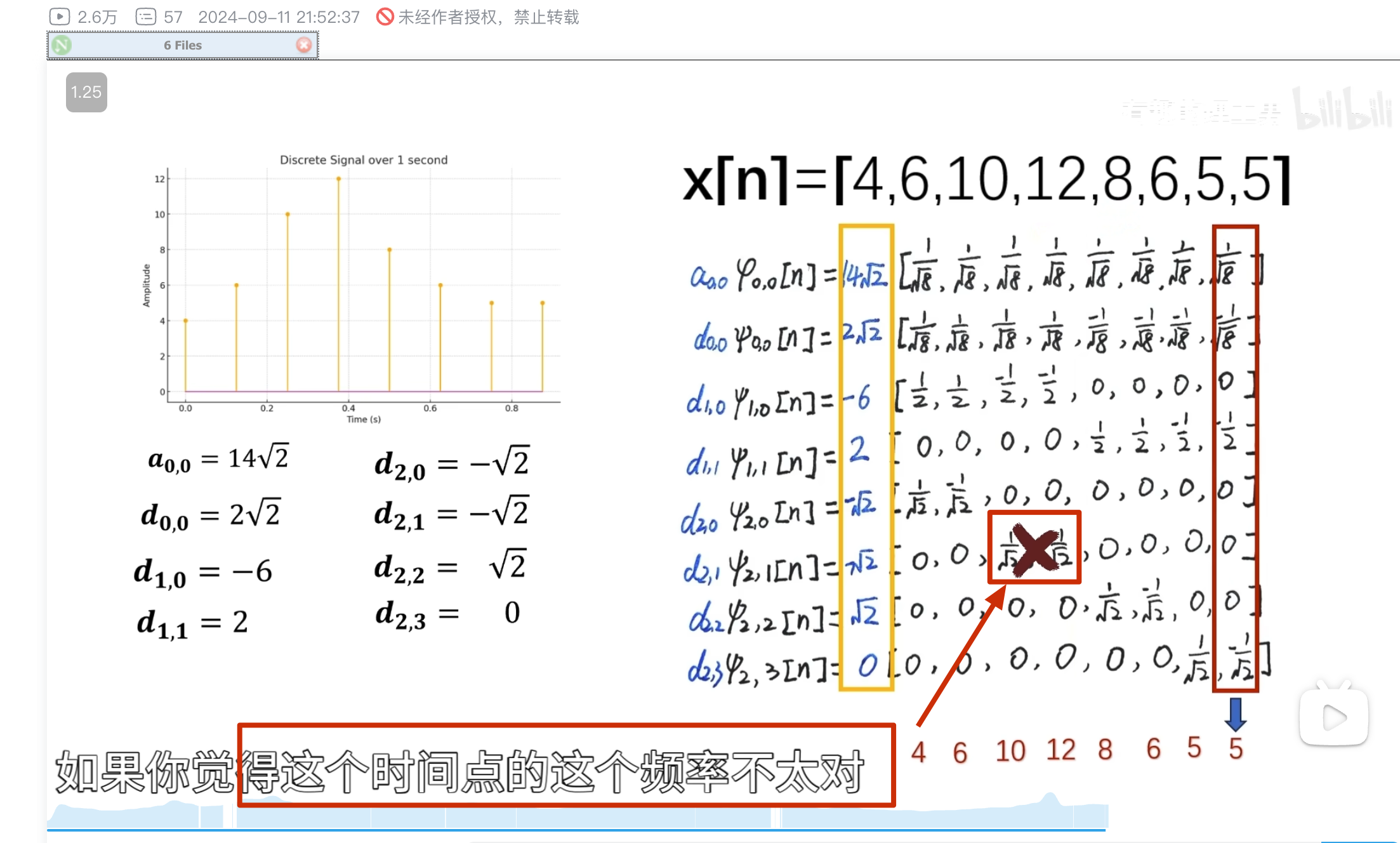
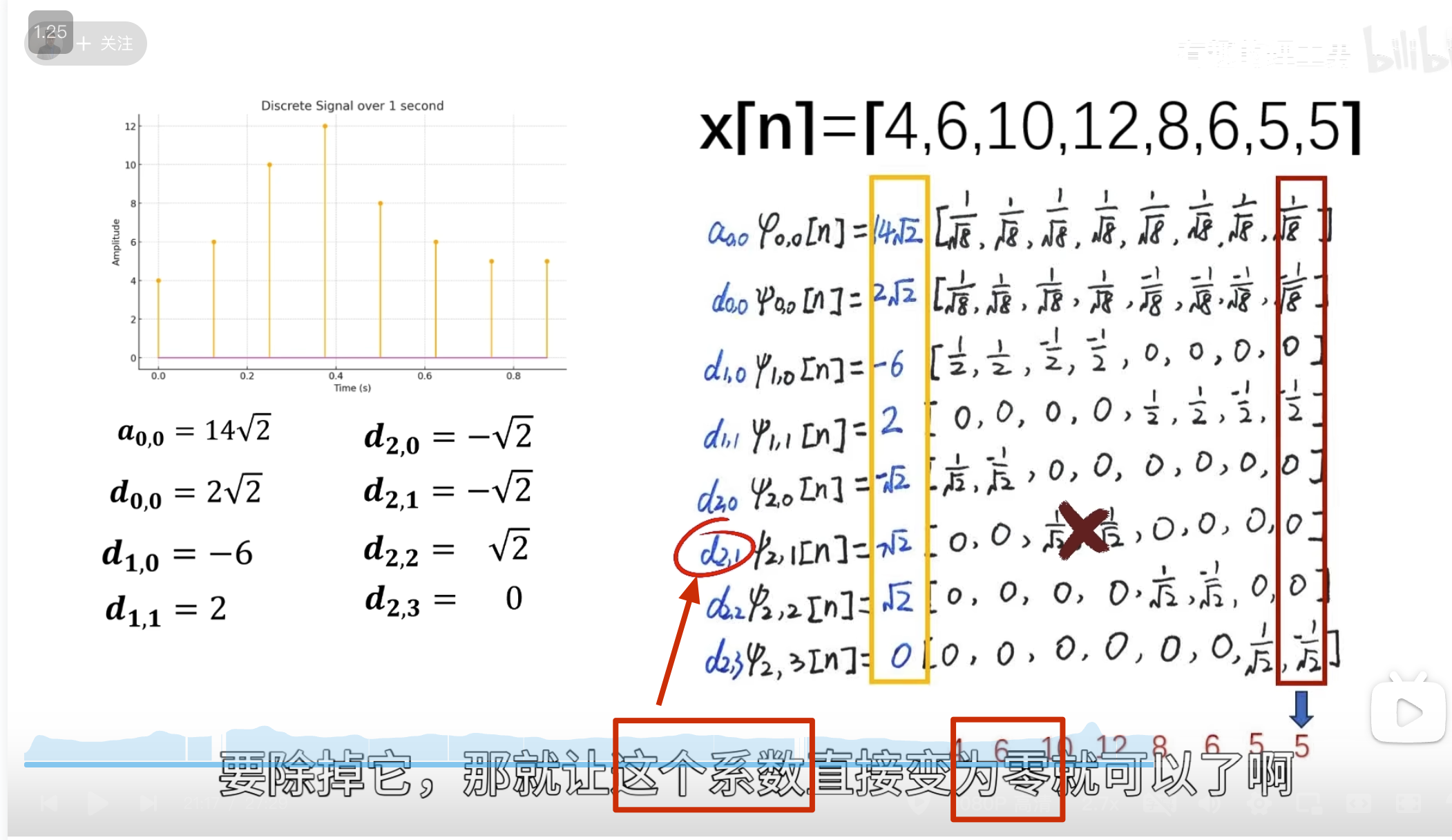























消失矩




























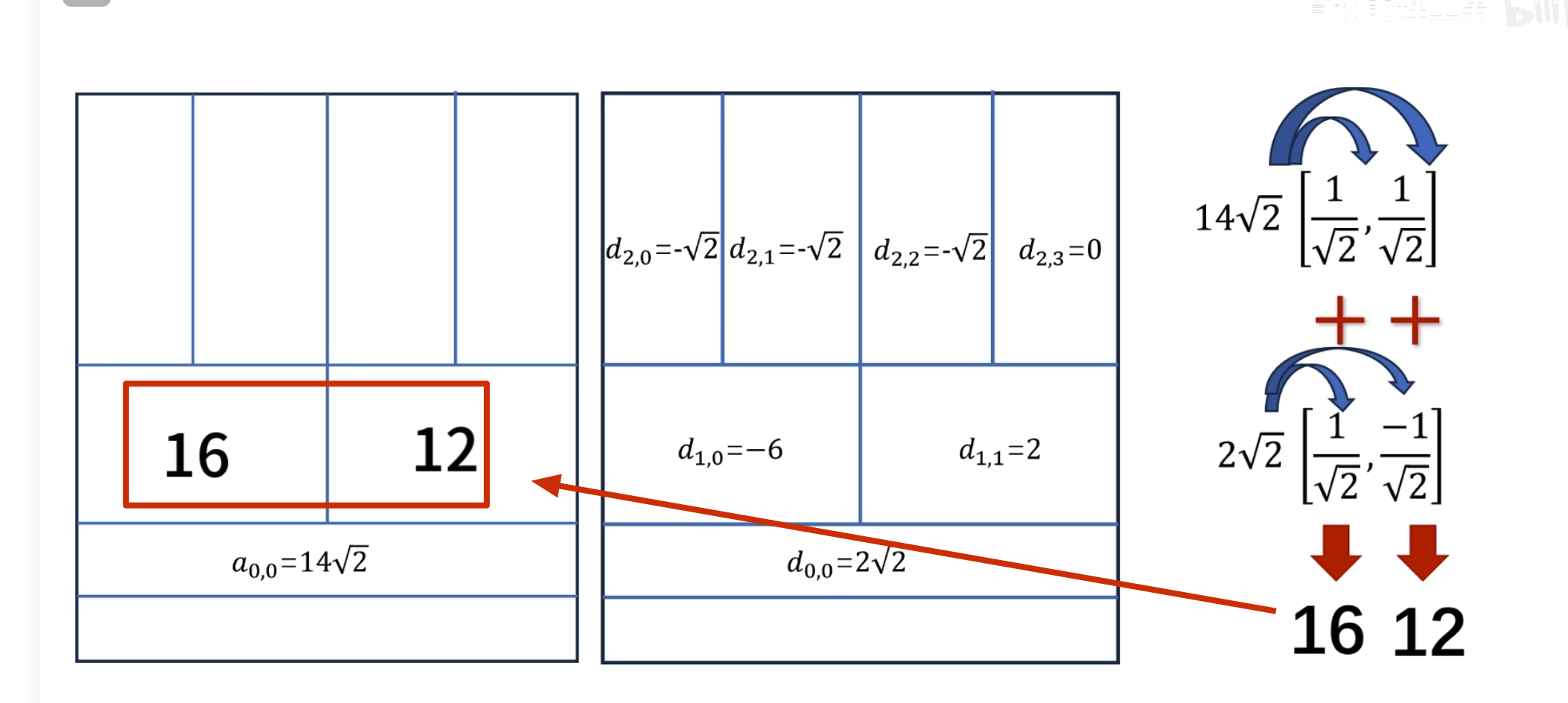
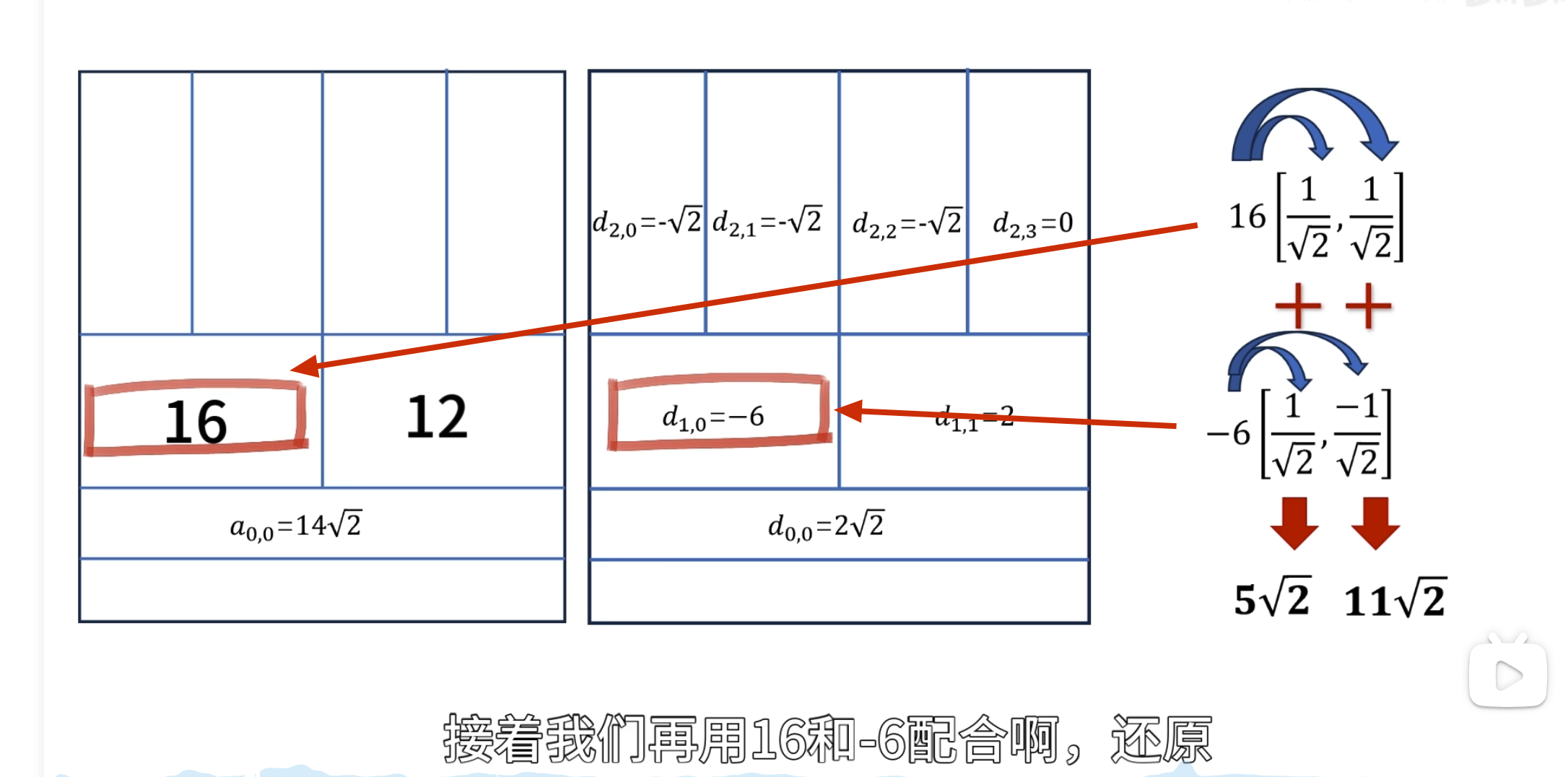
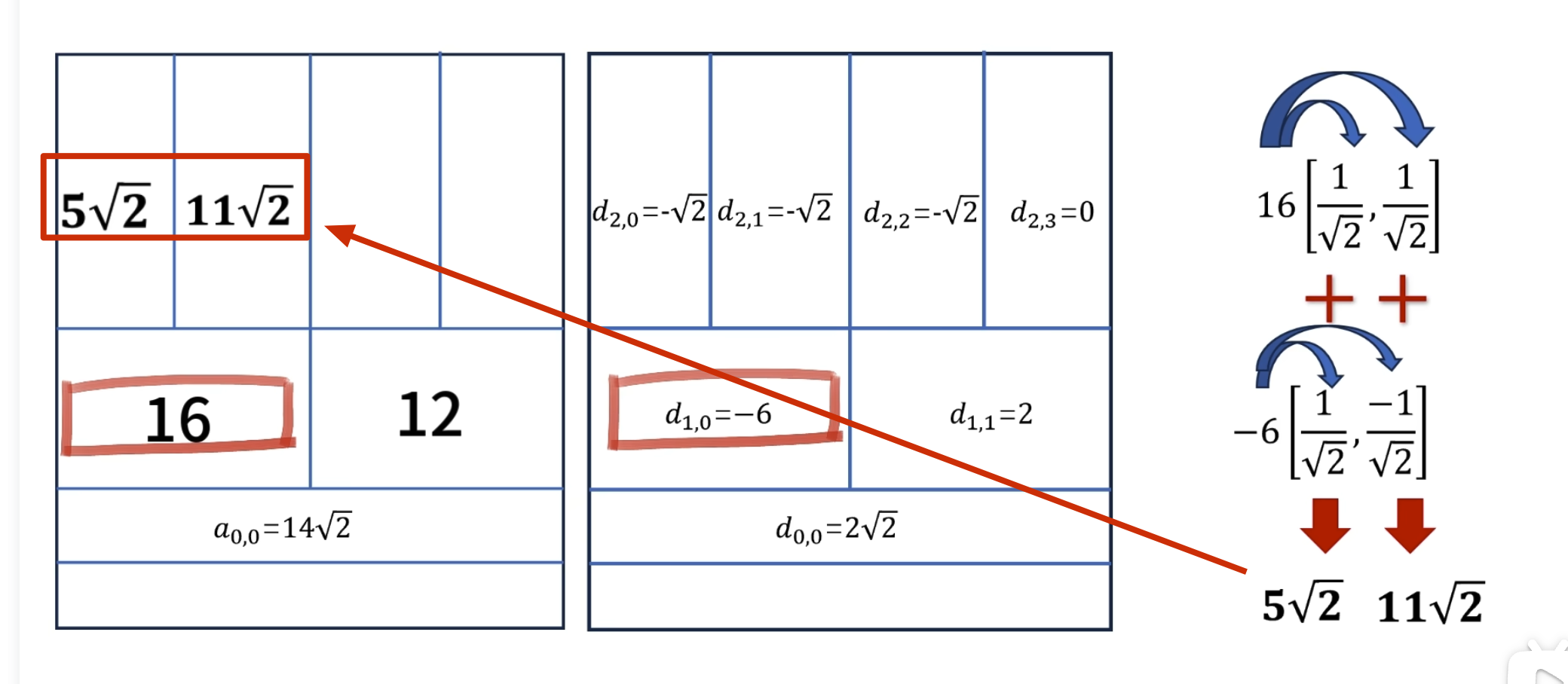

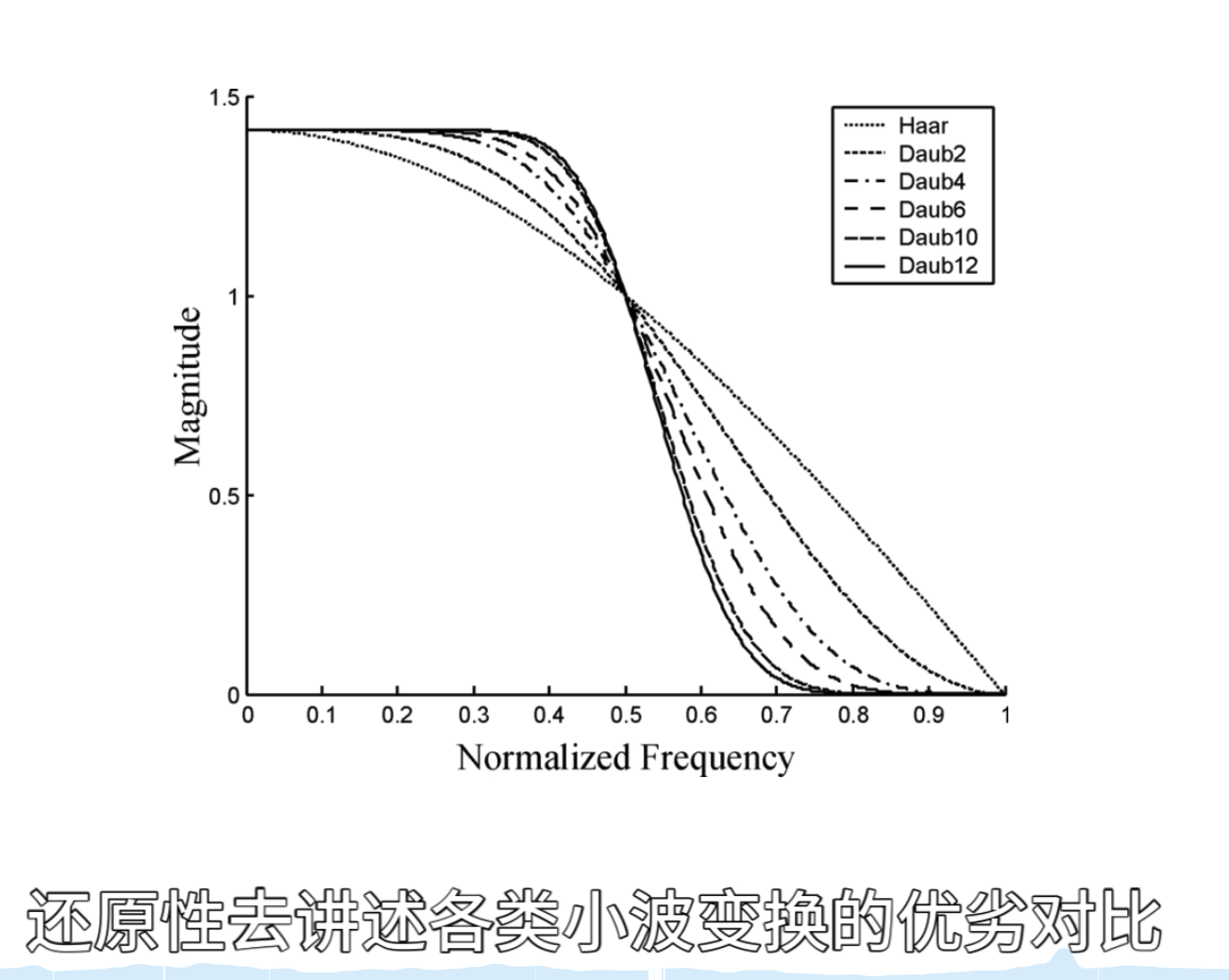



如何自己构造离散小波
一般滤波器的设计思路
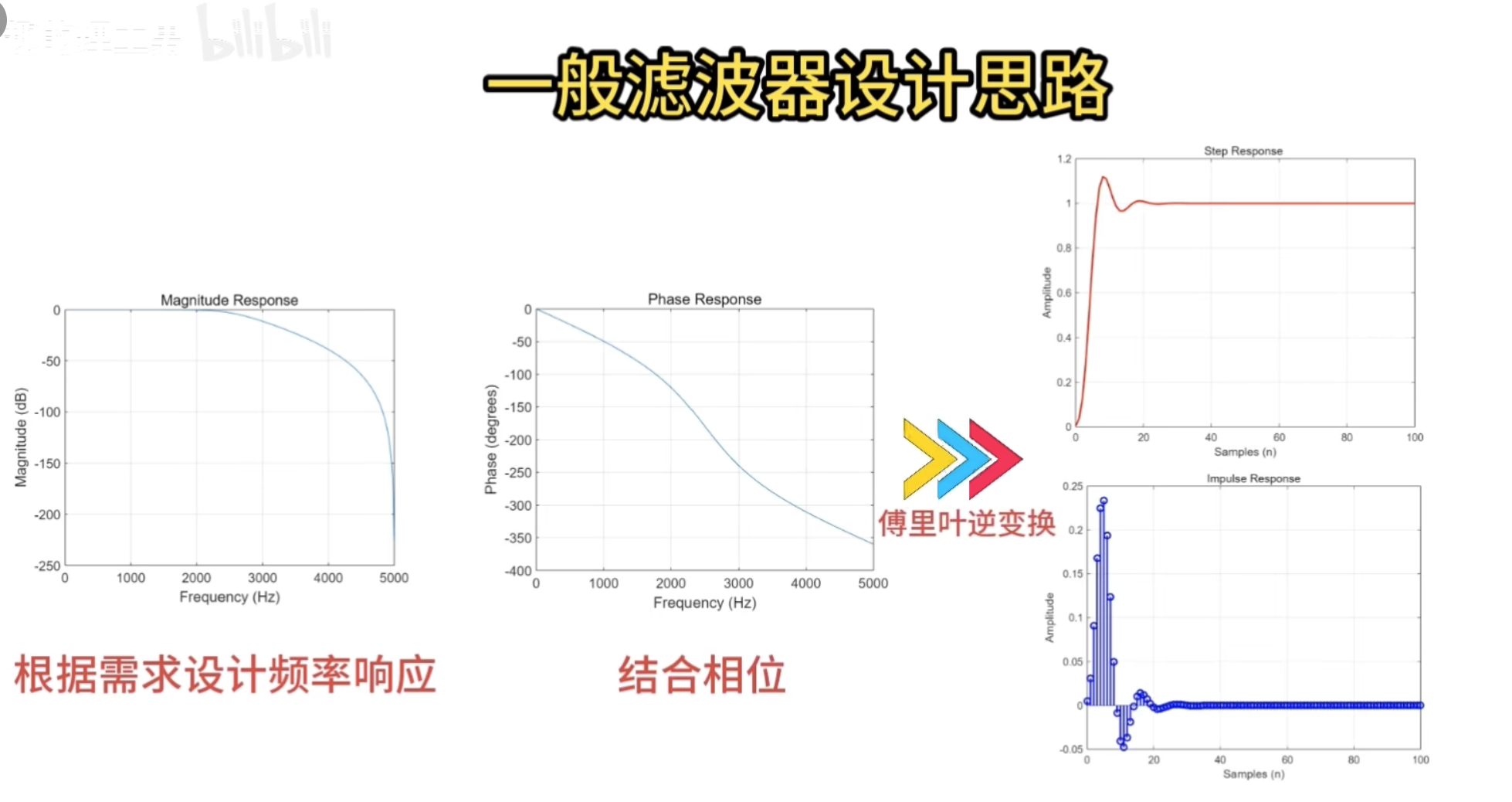
离散小波滤波器

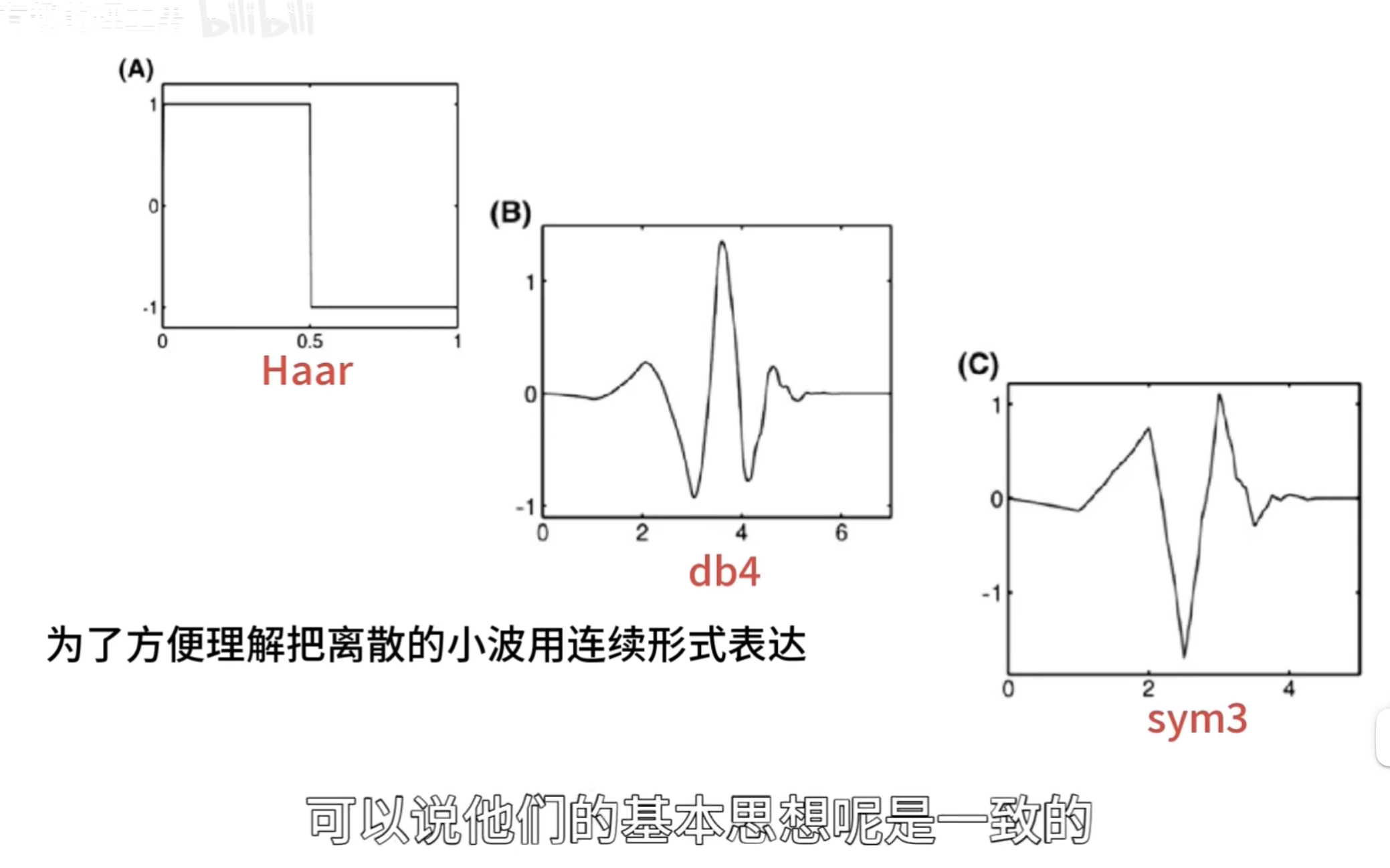
紧支撑性
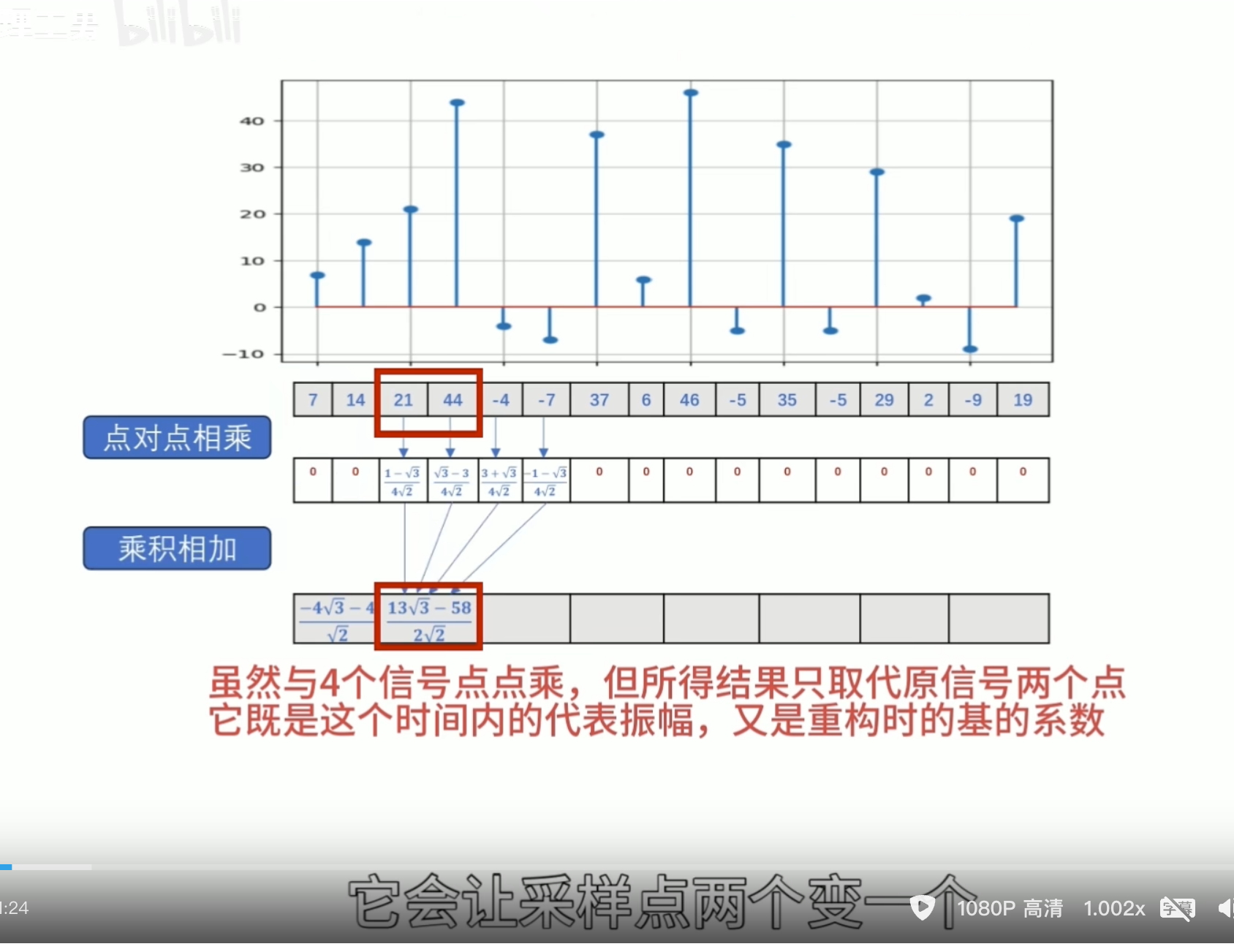
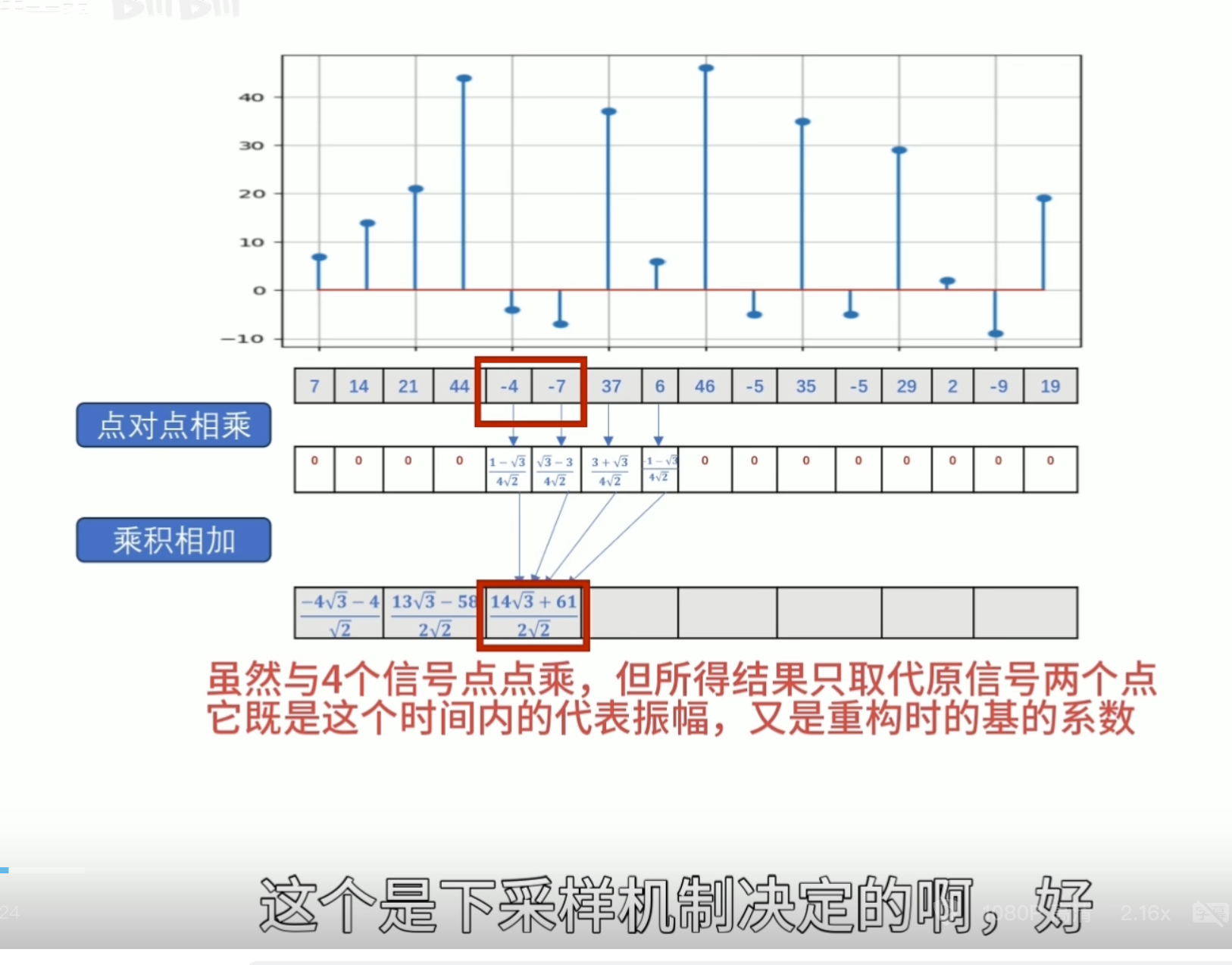
正交性
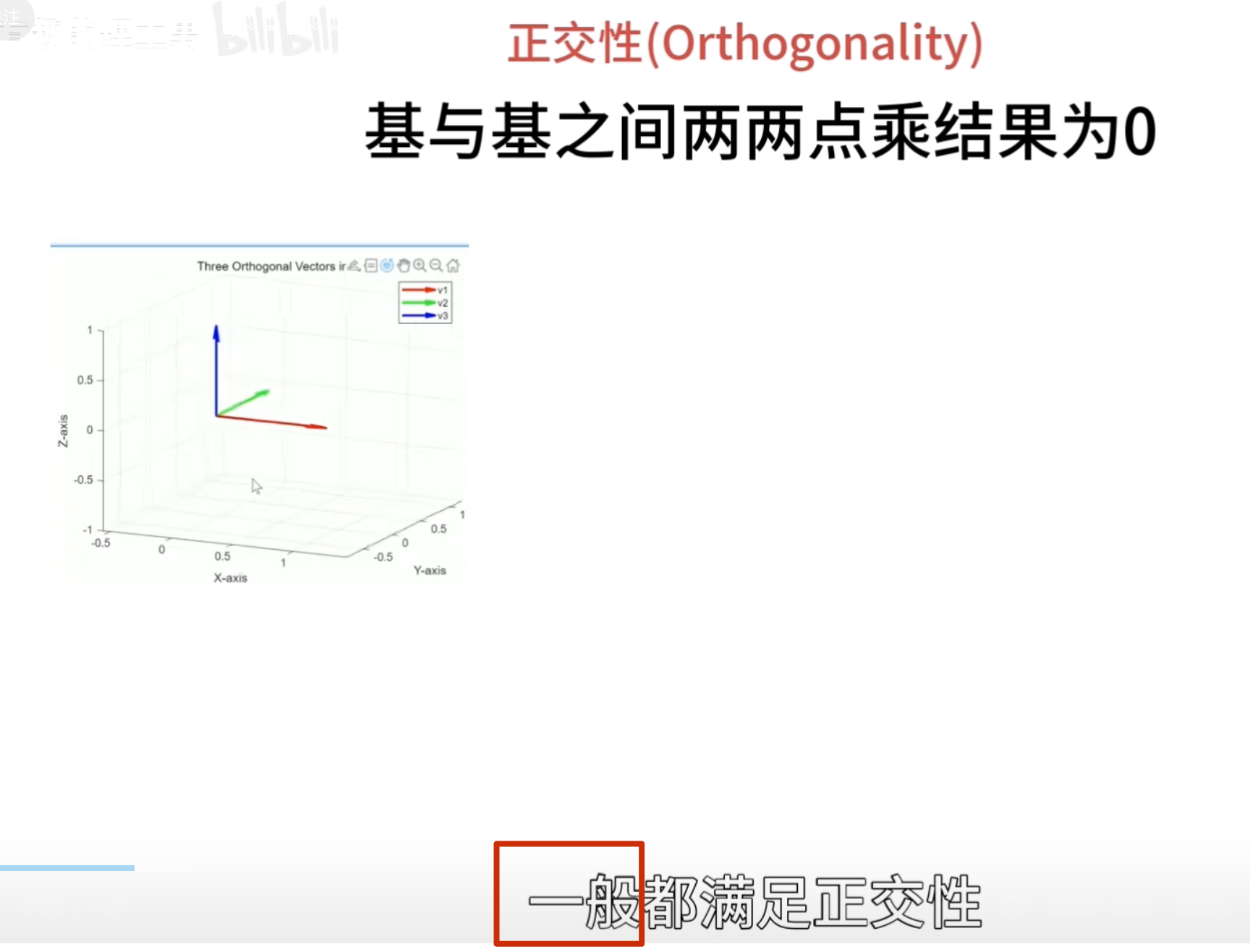







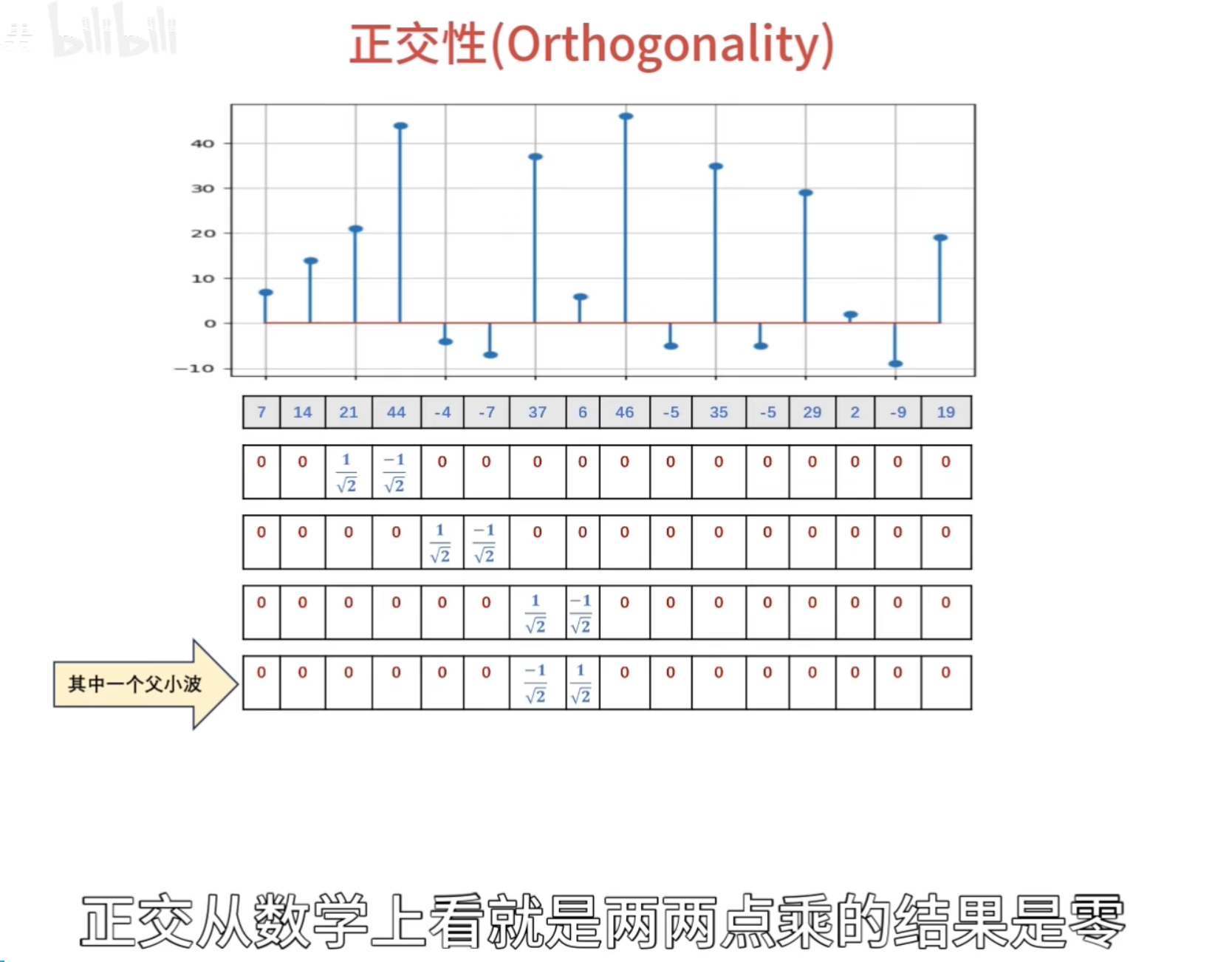
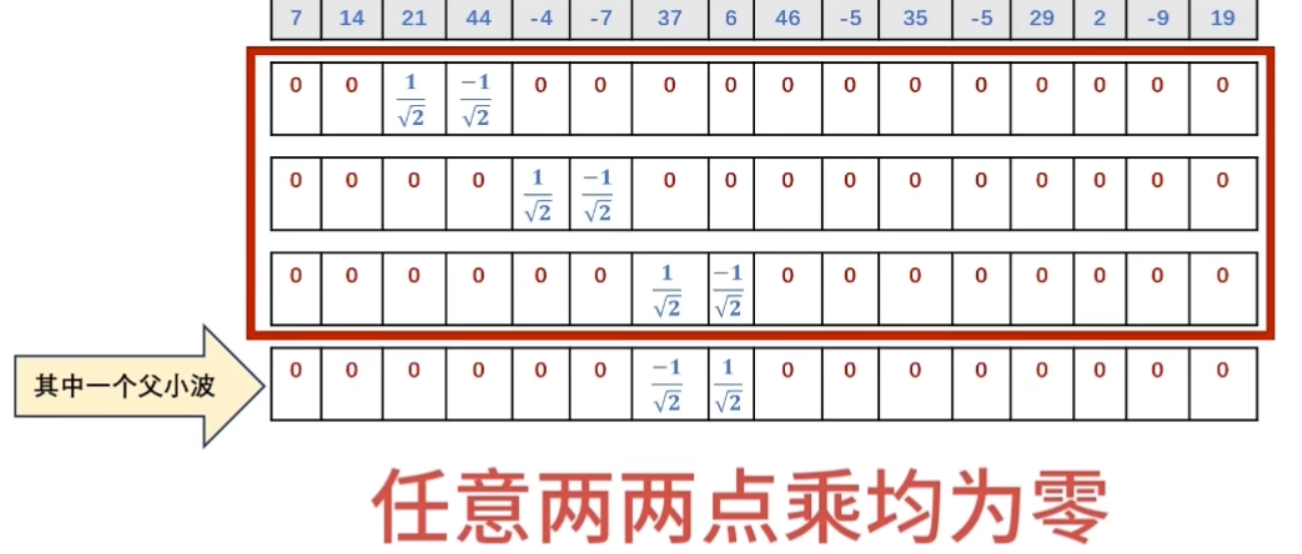



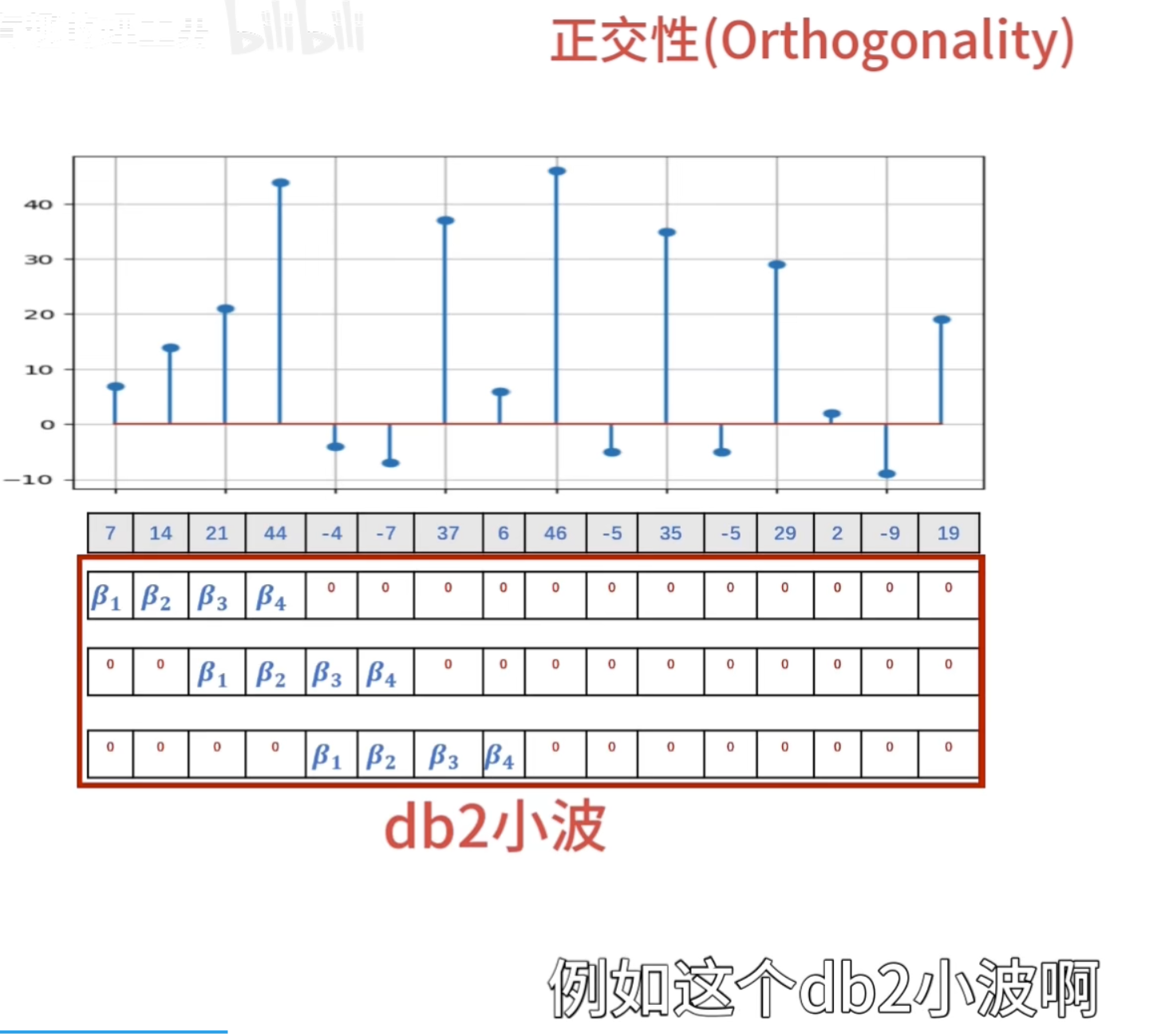








归一化
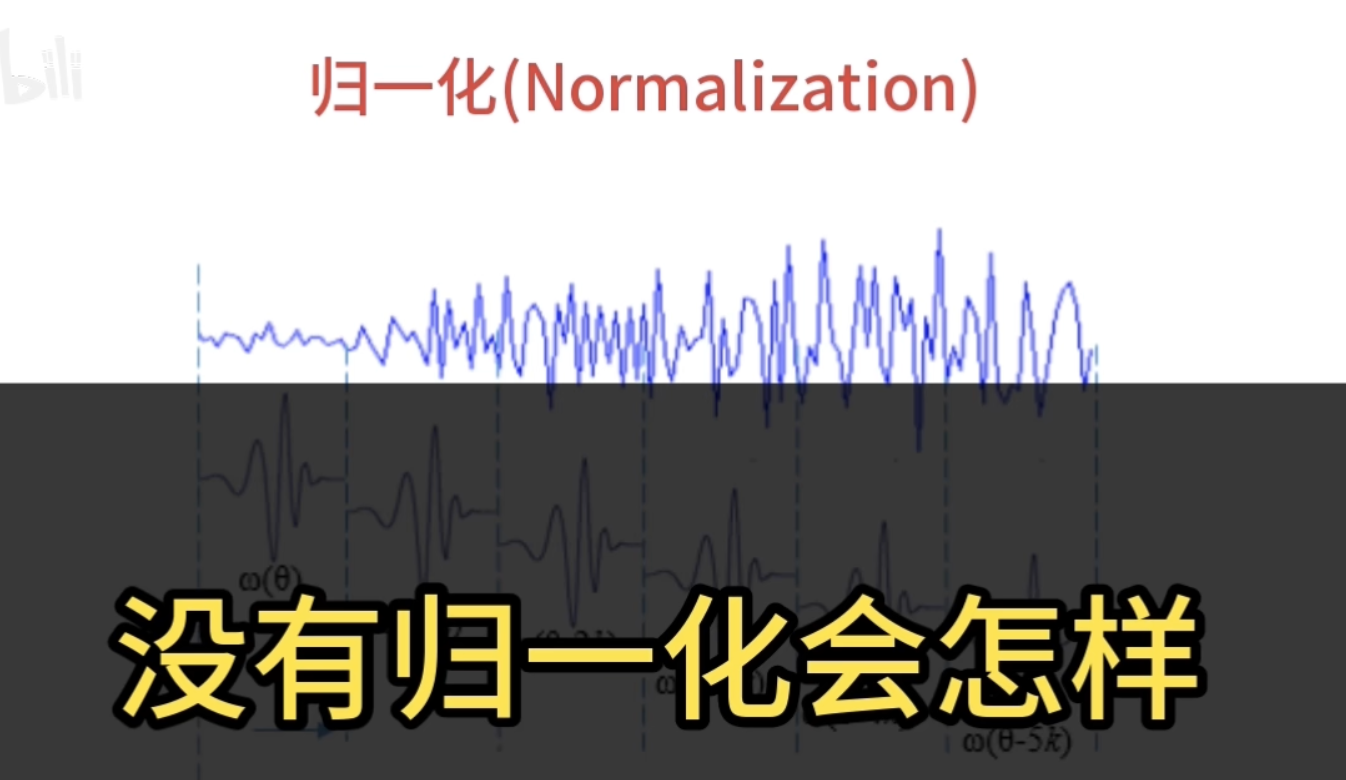

还原的结果是错的
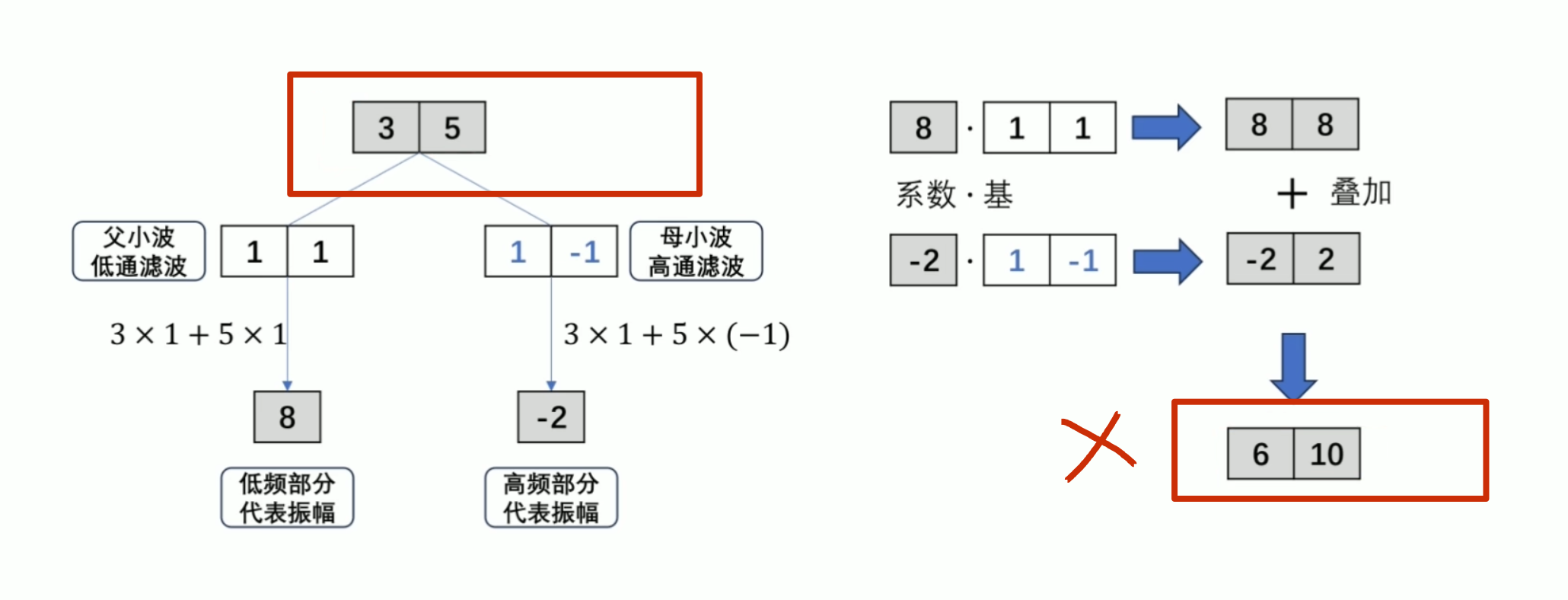
有归一化的结果
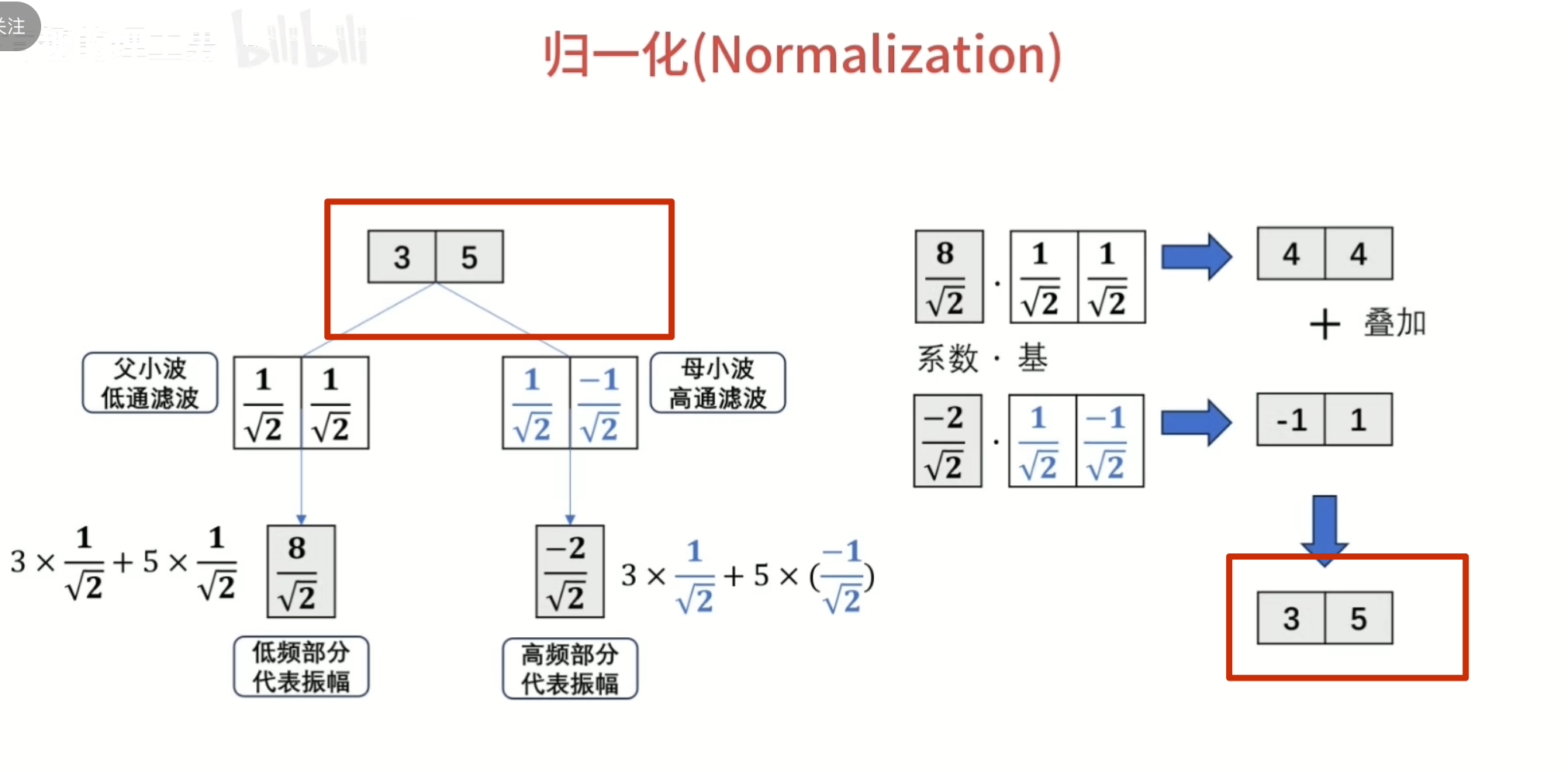
怎么归一化?
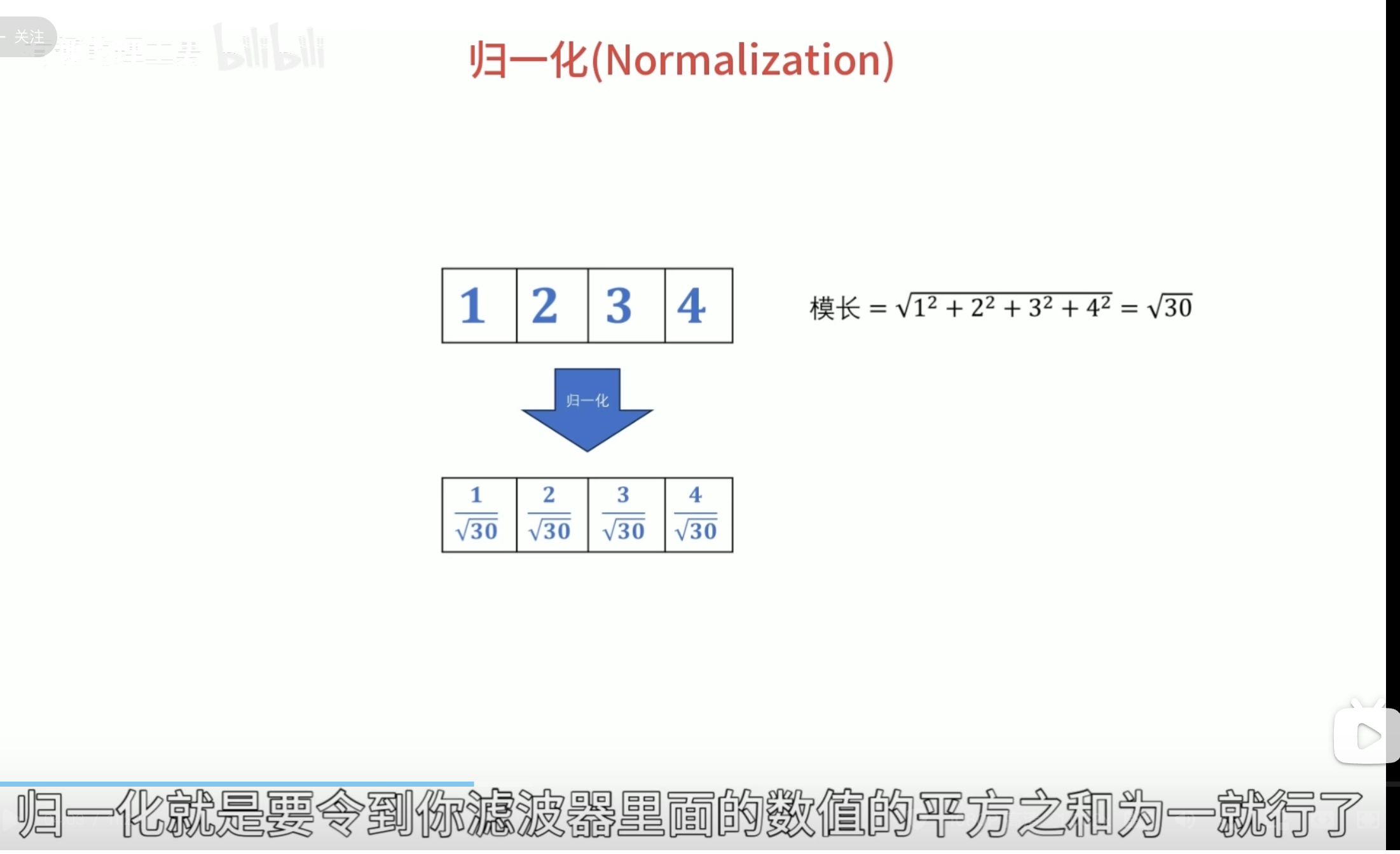
零均值(Zero Mean)
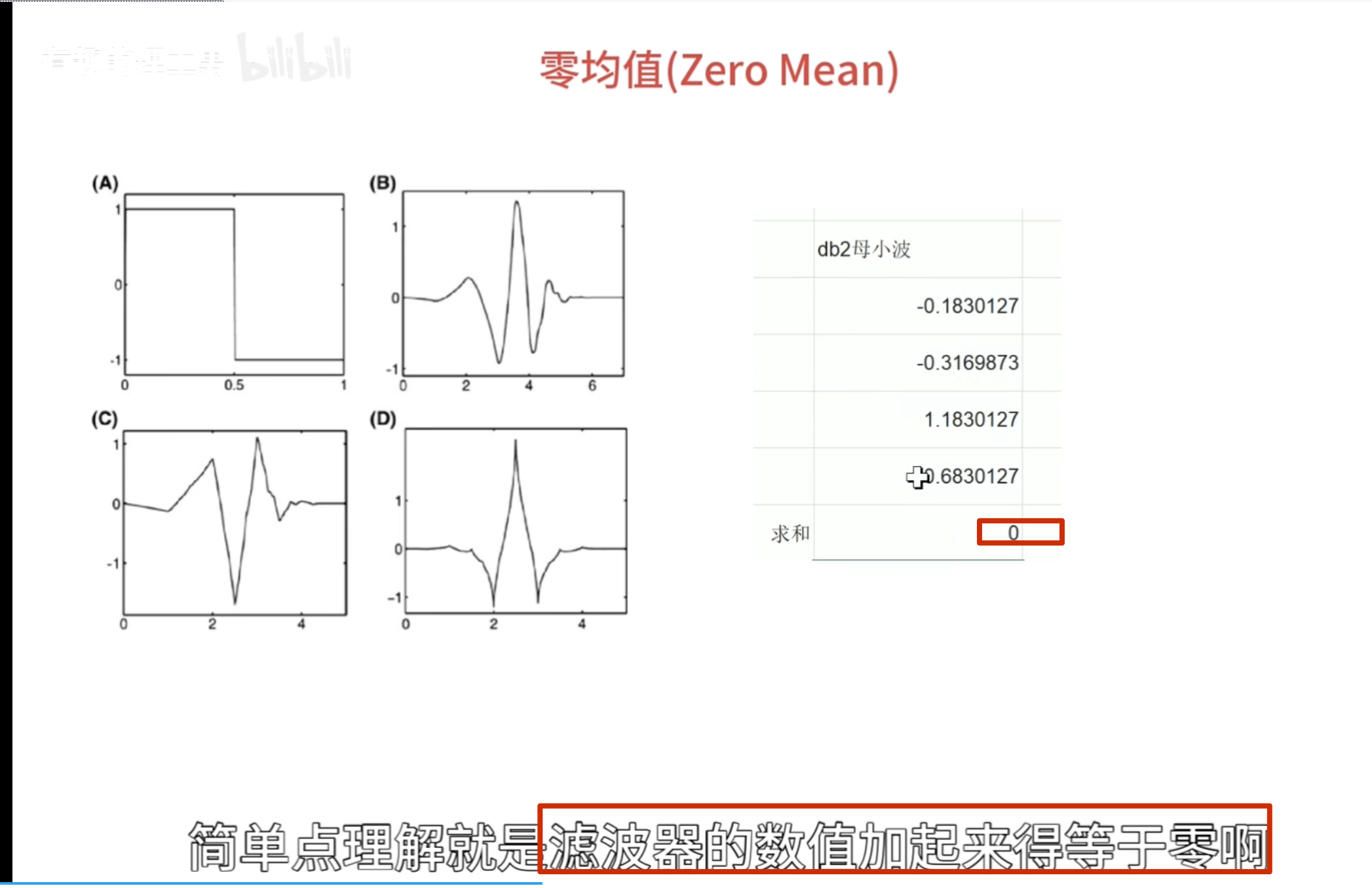



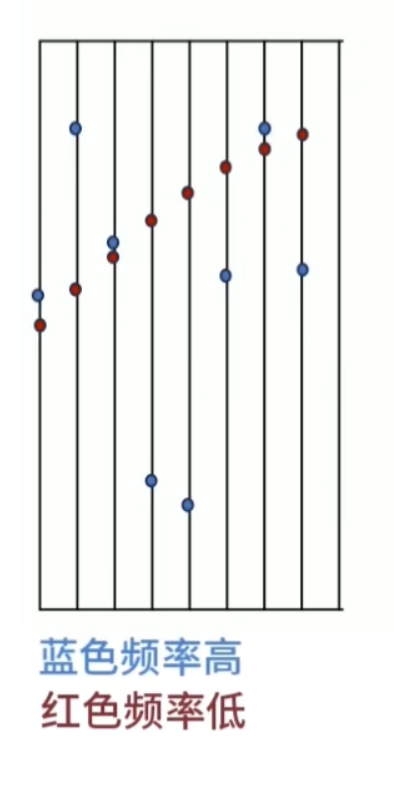







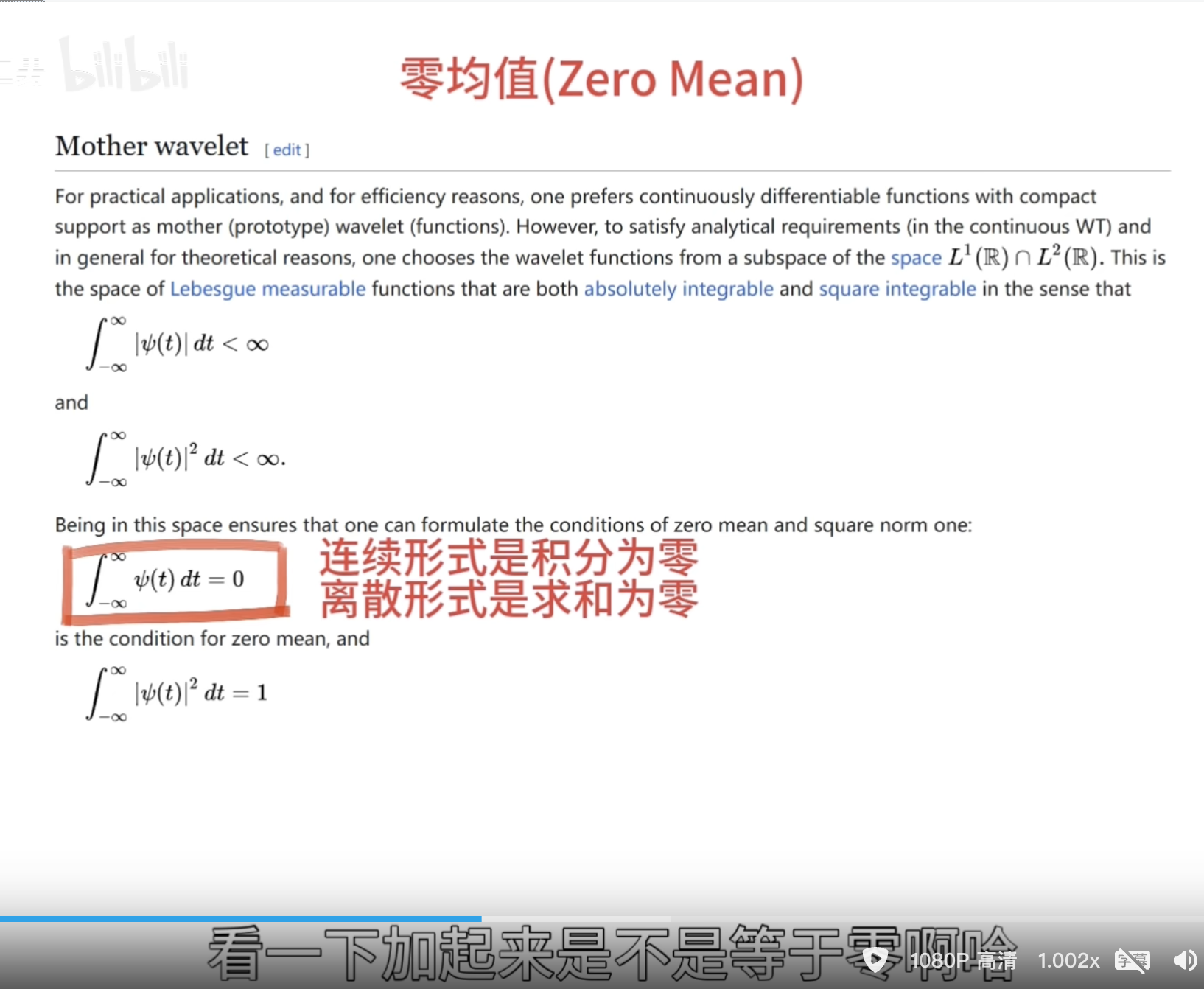
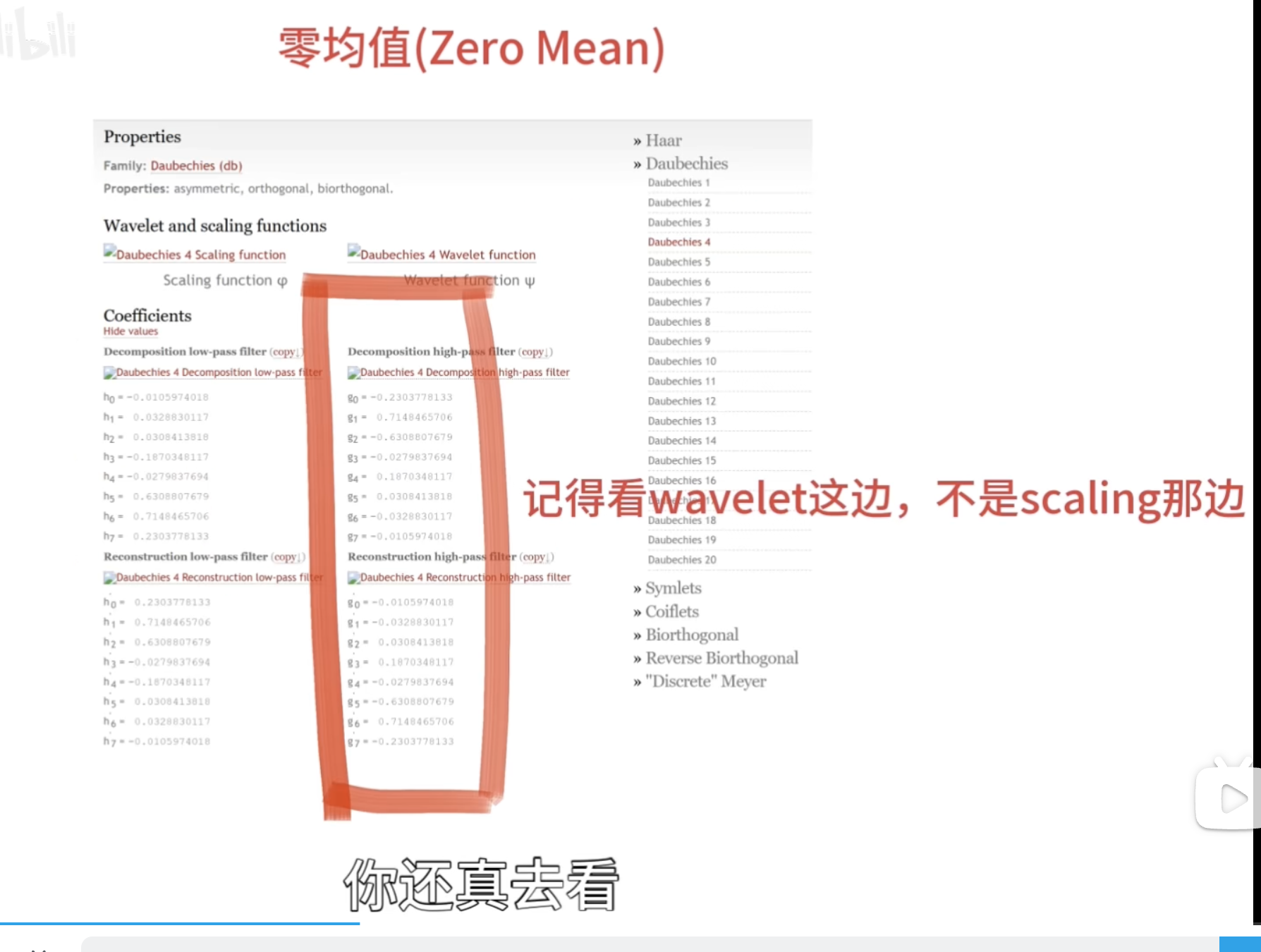
消失矩(vanishing moments)

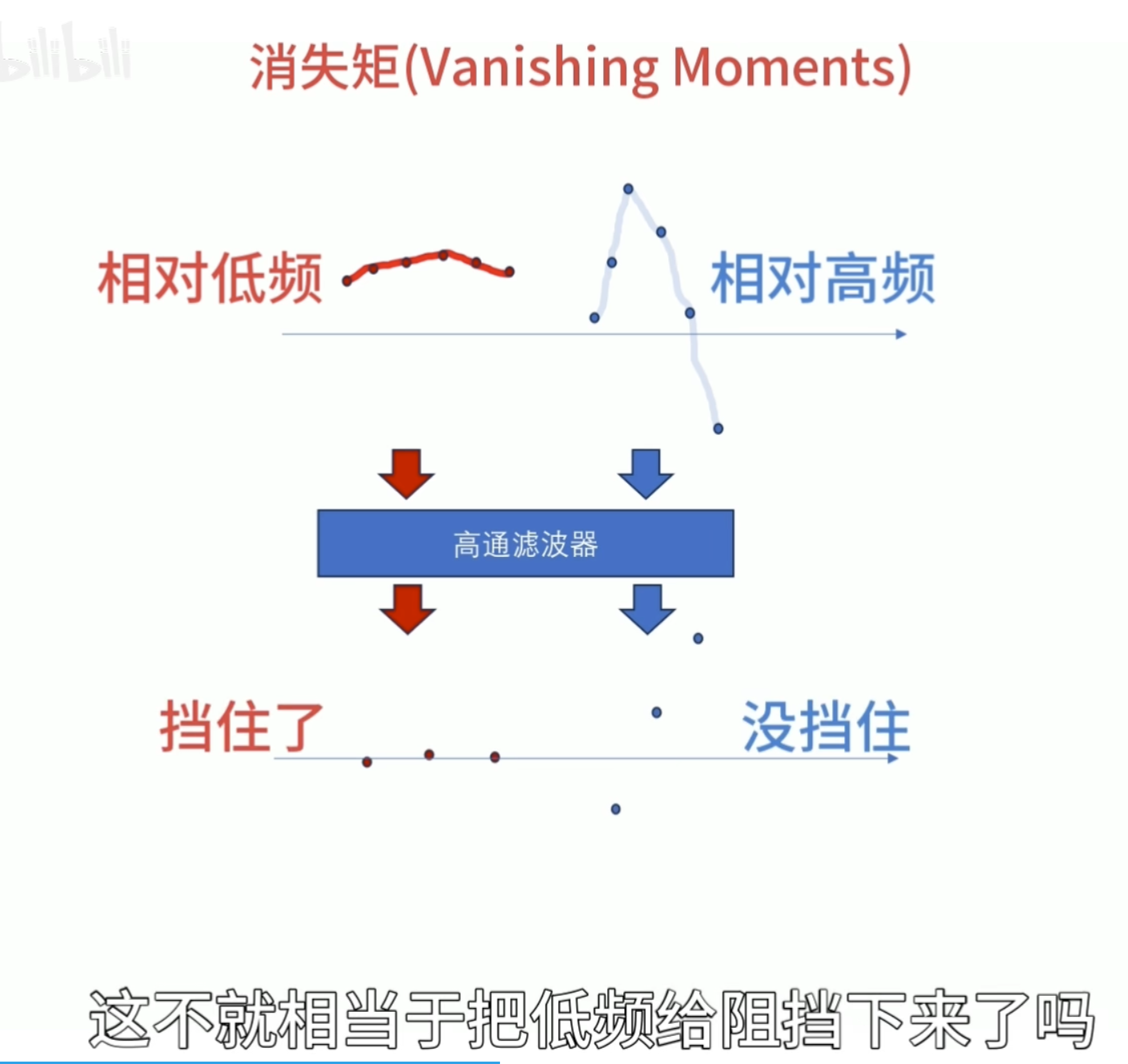


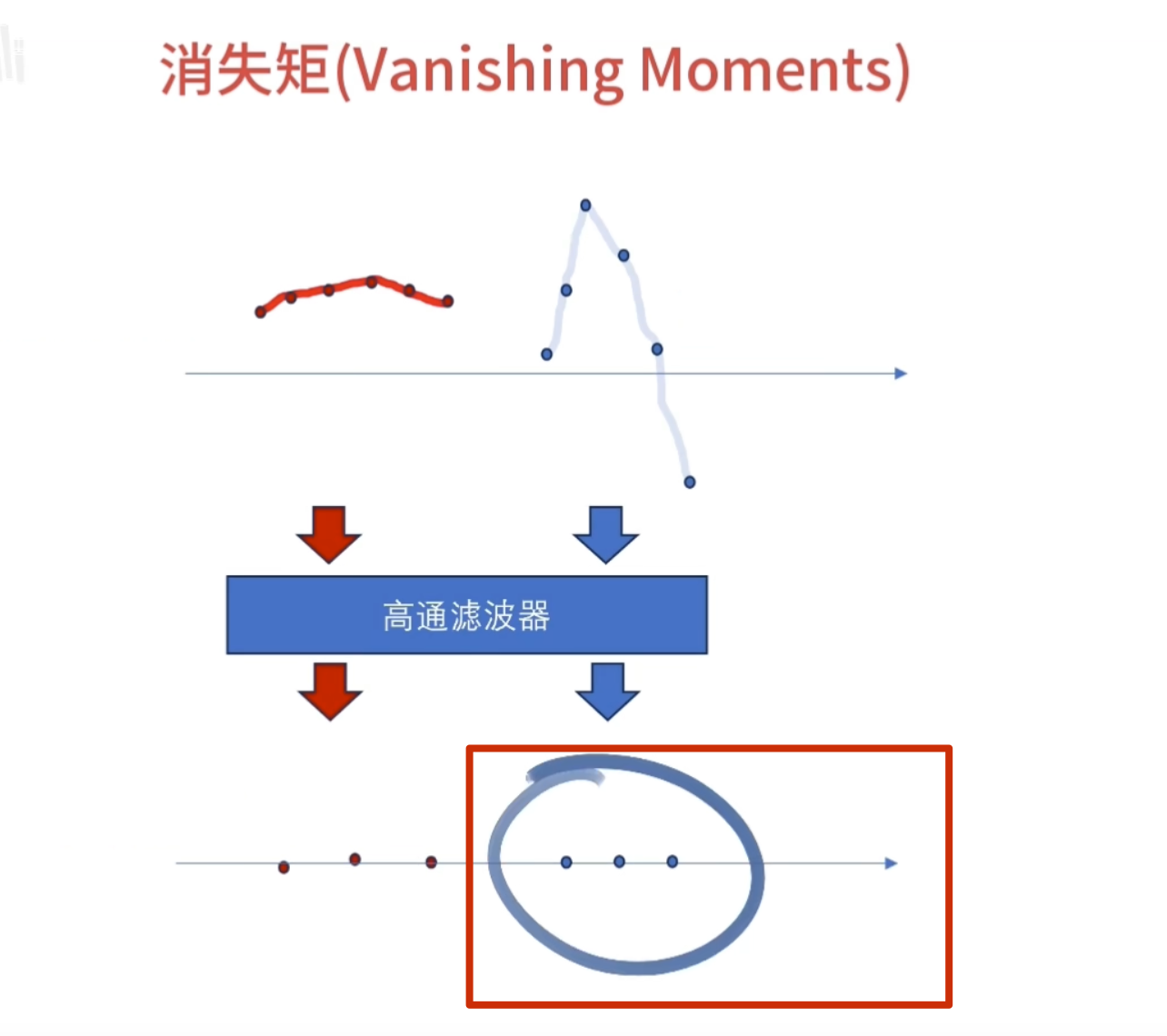





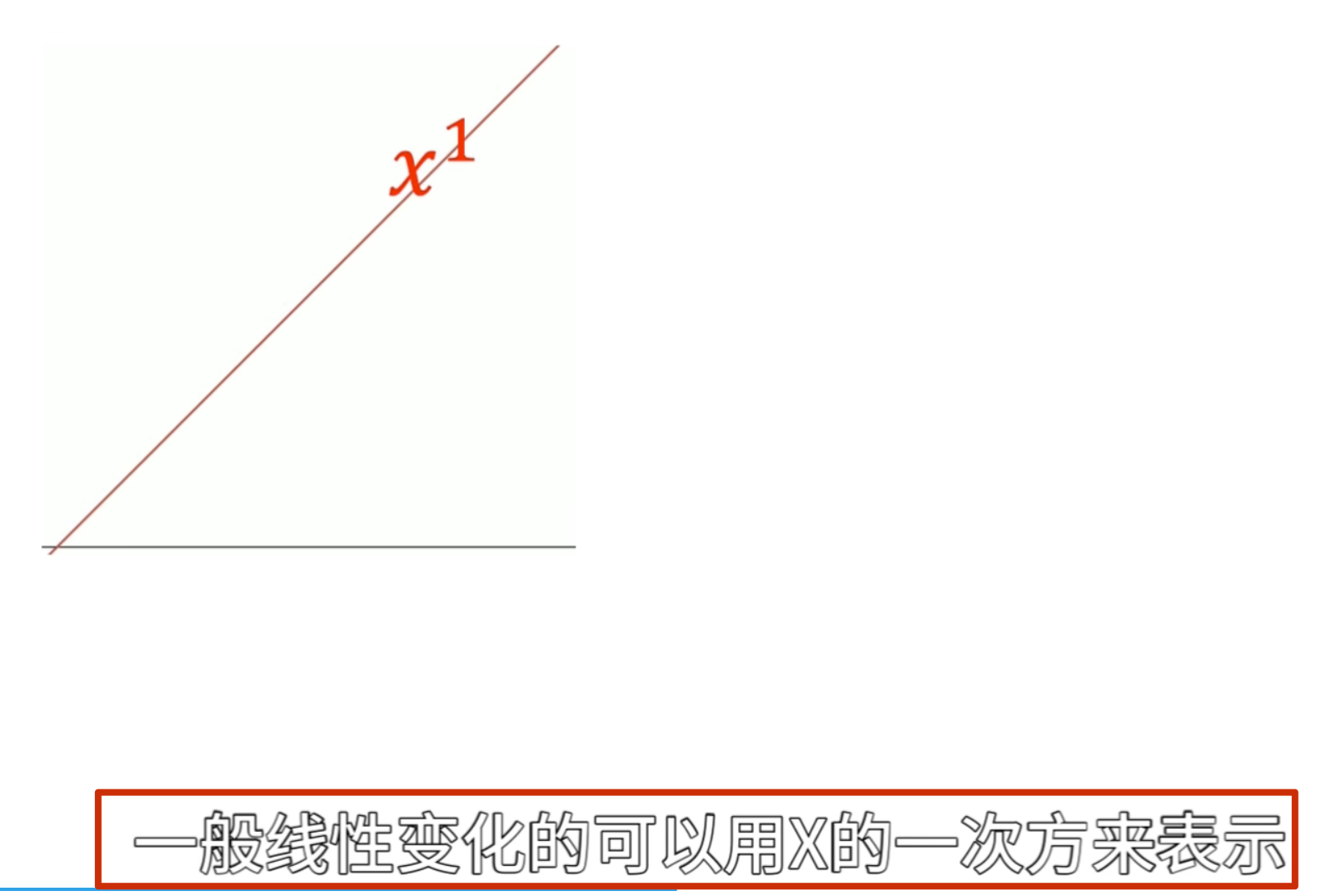


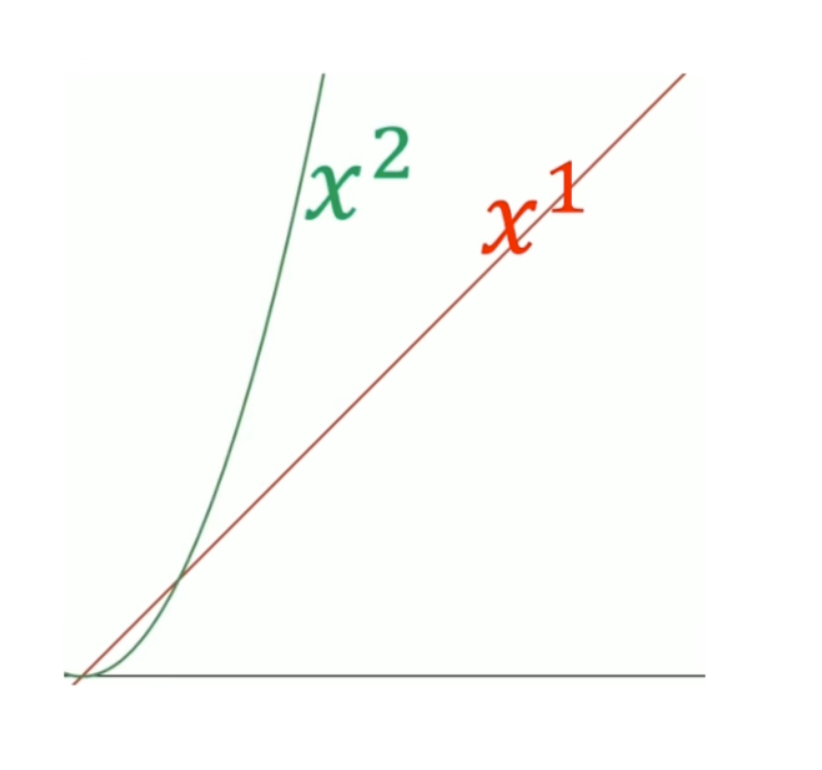



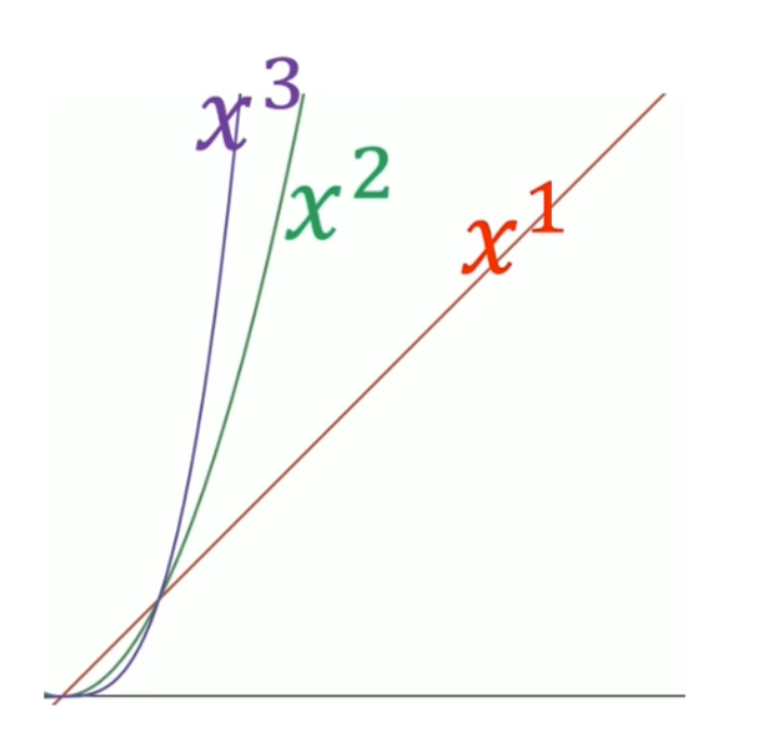


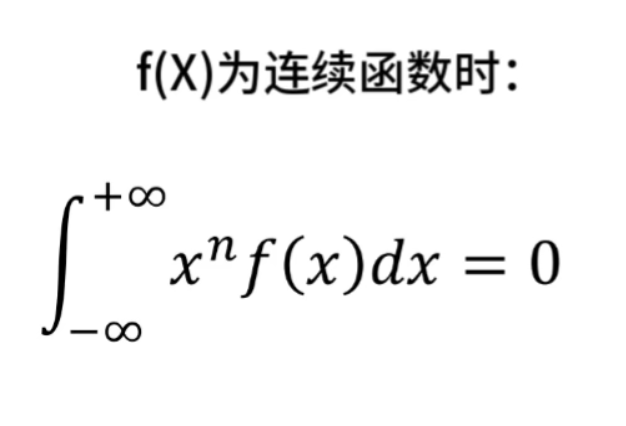





离散滤波器的消失矩

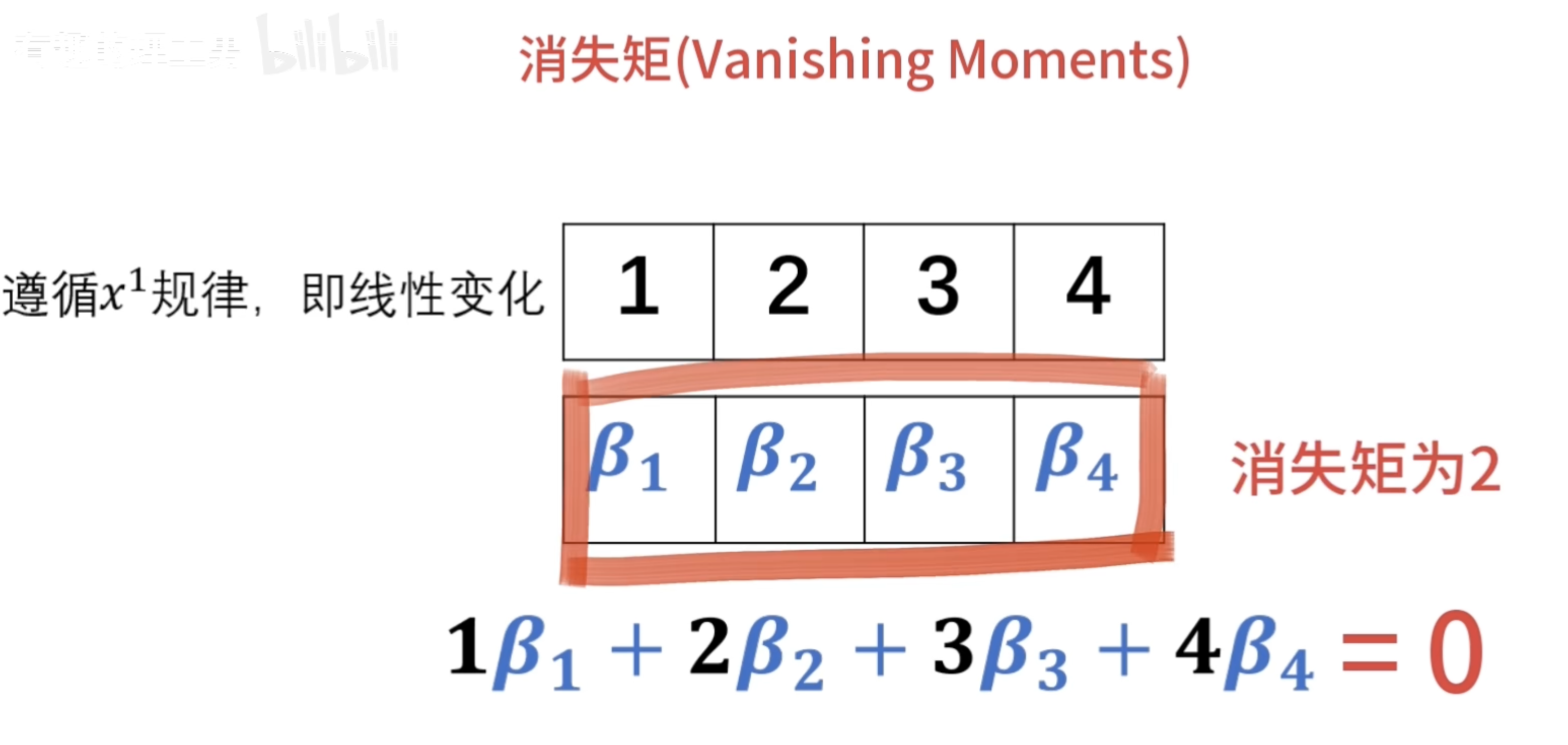

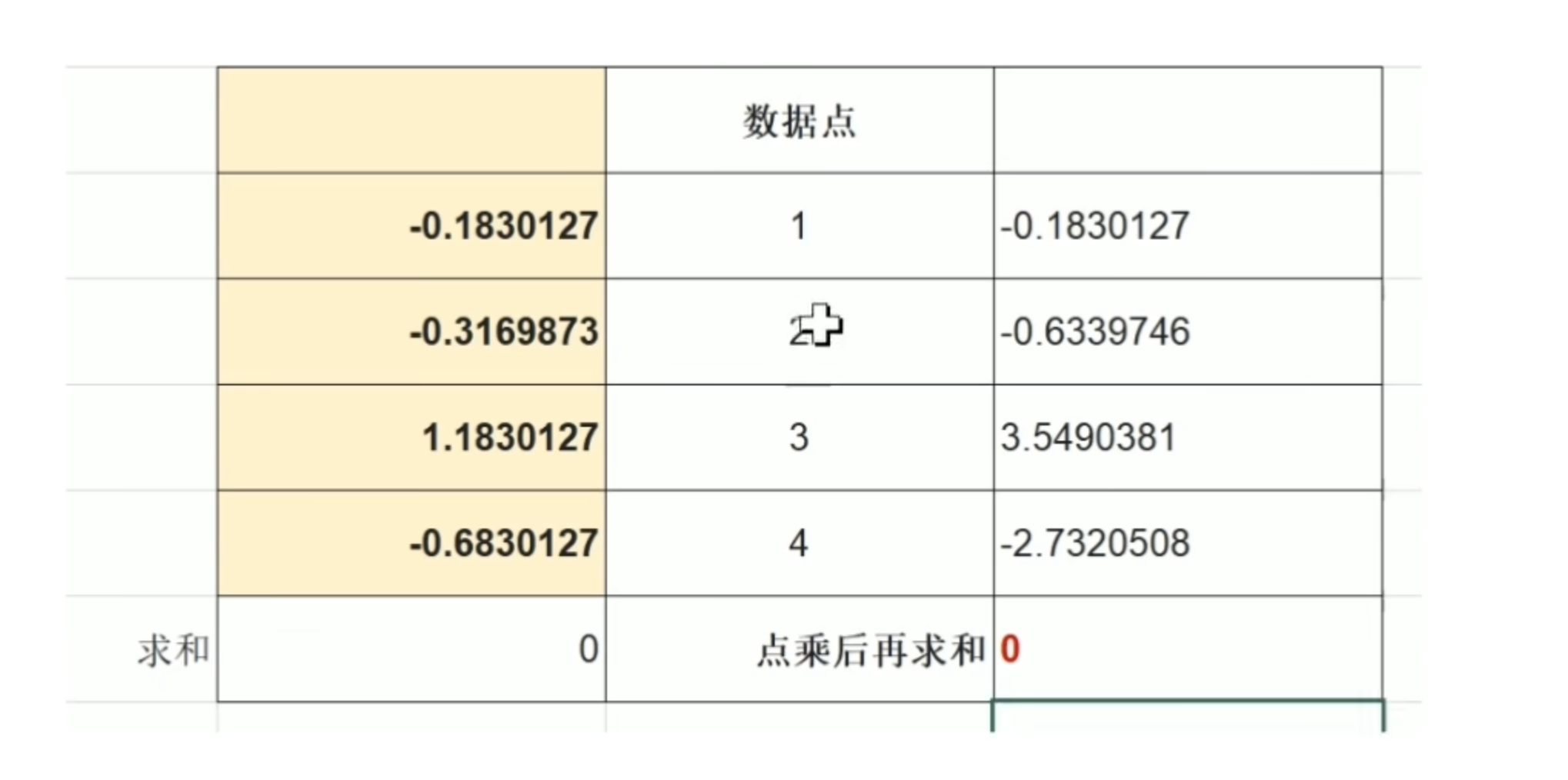


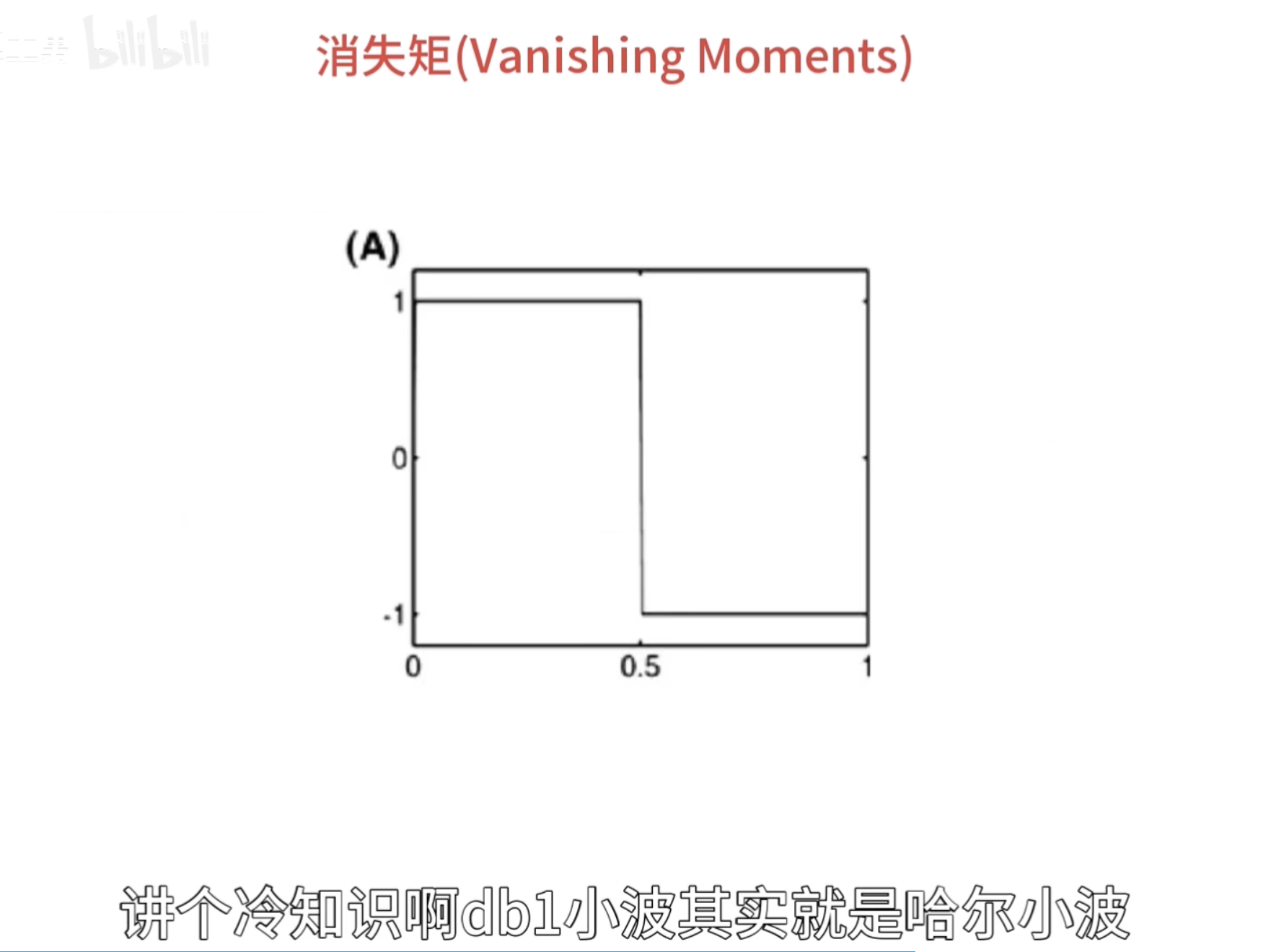
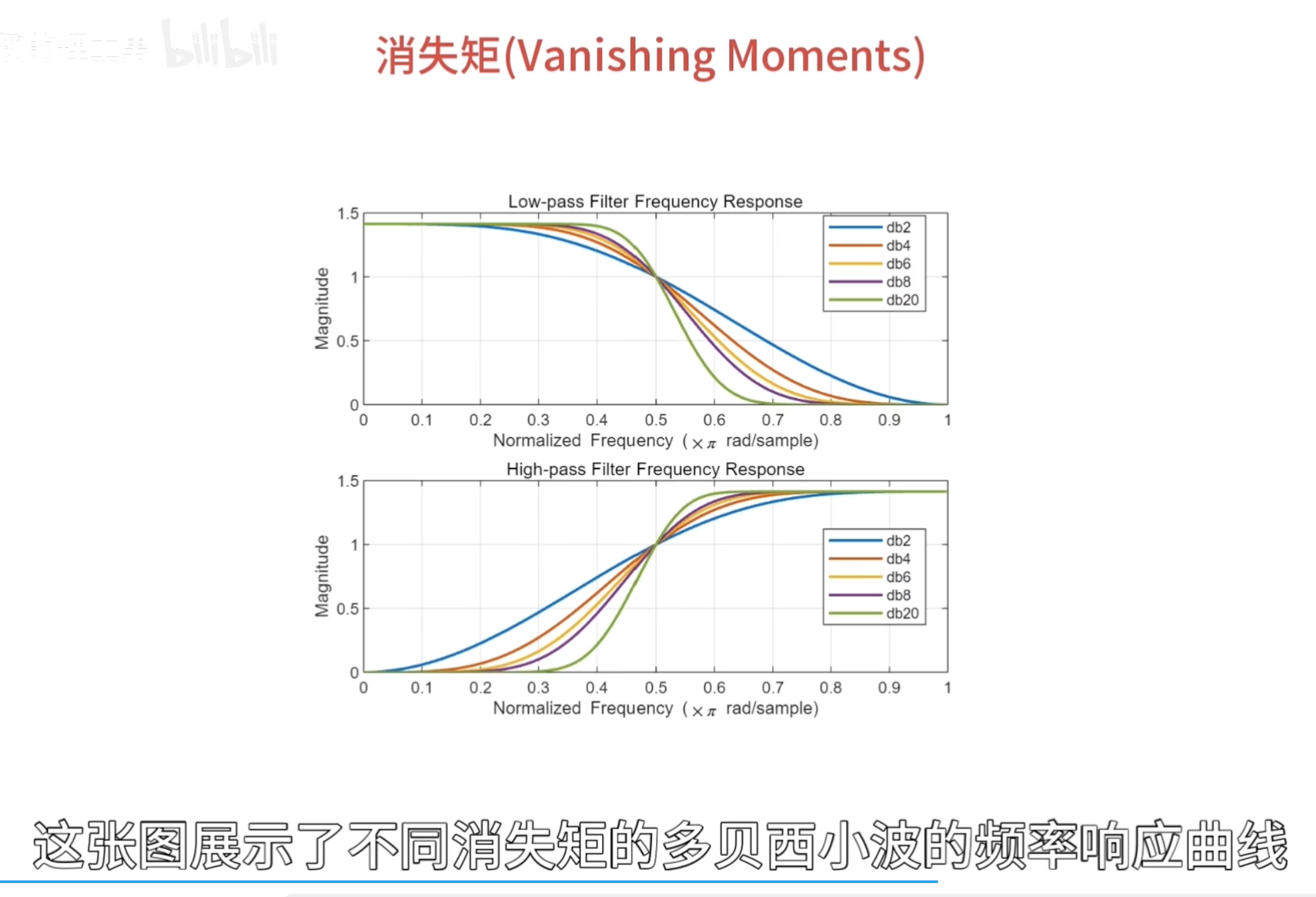




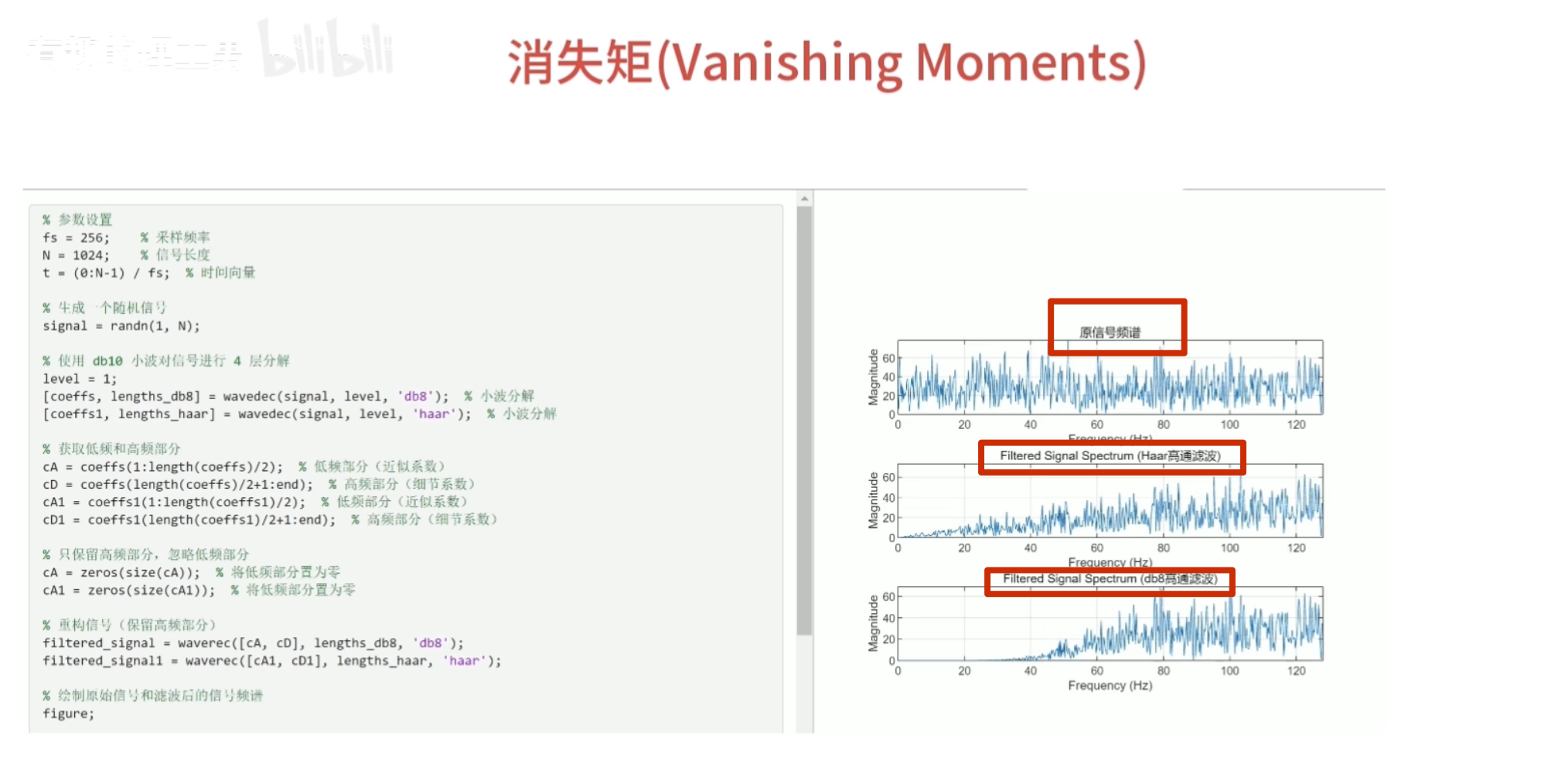


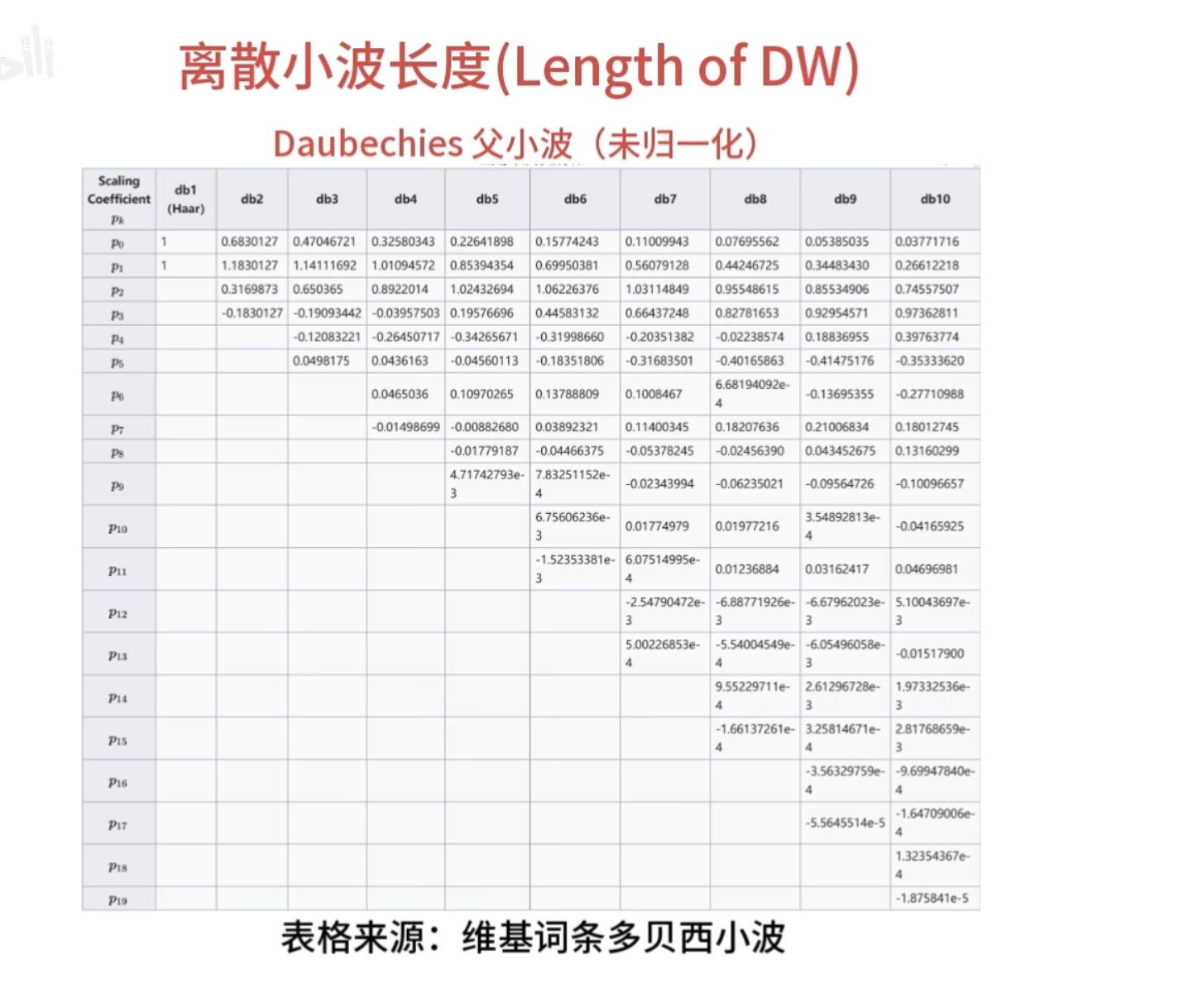
必须为偶数,否则无法正交













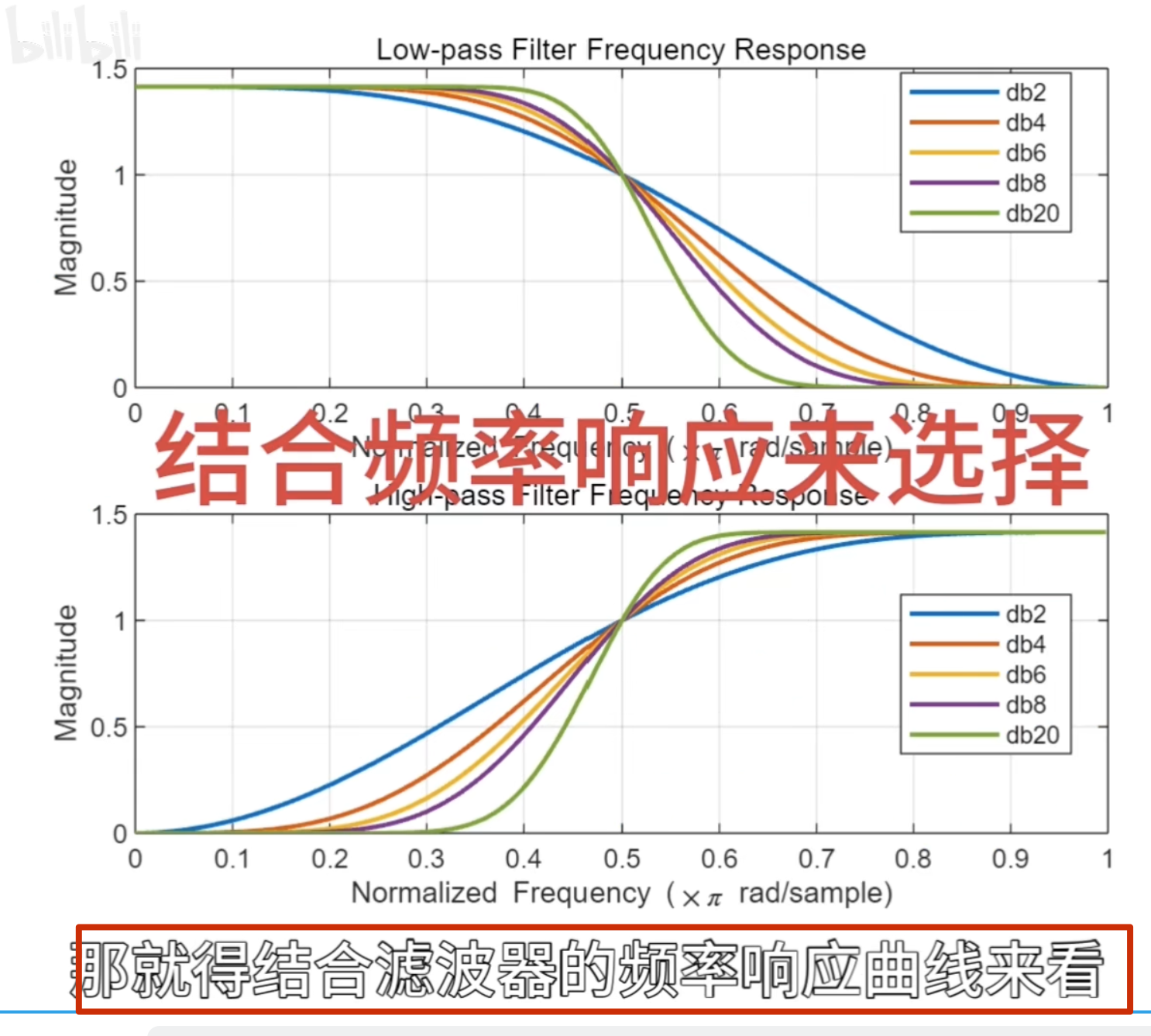



所以

训练集、验证集和测试集
在机器学习中,训练集、验证集和测试集都有着重要的作用。
一、训练集(Training Set)
定义:训练集是用来训练模型的数据集合。它包含输入数据和对应的目标输出(标签),模型通过学习这些数据中的模式和规律来调整自身的参数,以最小化预测误差。
作用:
- 模型学习:训练集是模型学习的基础,通过在训练集上进行迭代训练,模型逐渐提高对数据的拟合能力,学习到数据中的特征和规律。
- 参数调整:利用训练集上的误差反馈,通过优化算法(如梯度下降)不断调整模型的参数,使模型能够更好地适应数据的分布。
二、验证集(Validation Set)
定义:验证集是在模型训练过程中用于评估模型性能和调整超参数的数据集合。它独立于训练集,通常从原始数据中划分出来。
作用:
- 性能评估:在模型训练的不同阶段,使用验证集来评估模型的性能,如准确率、损失值等指标。通过观察模型在验证集上的表现,可以了解模型是否过拟合或欠拟合。
- 超参数调整:验证集用于调整模型的超参数,如学习率、层数、节点数等。通过在验证集上进行实验,选择性能最佳的超参数组合。
- 早停法(Early Stopping):当模型在验证集上的性能不再提升时,可以停止训练,防止过拟合。
三、测试集(Test Set)
定义:测试集是用于最终评估模型性能的数据集合。它与训练集和验证集完全独立,在模型训练过程中不被使用。
作用:
- 最终性能评估:测试集提供了一个客观的评估标准,用于衡量模型在未知数据上的泛化能力。通过在测试集上的表现,可以确定模型的实际性能。
- 模型比较:当有多个模型时,可以使用测试集来比较它们的性能,选择性能最佳的模型。
- 模型部署决策:测试集的结果可以帮助决定是否将模型部署到实际应用中。如果模型在测试集上的性能不理想,可能需要进一步改进模型或重新收集数据。
总之,训练集用于模型学习和参数调整,验证集用于性能评估和超参数调整,测试集用于最终评估模型的泛化能力和做出模型部署决策。合理划分和使用这三个数据集对于构建有效的机器学习模型至关重要。
自注意力机制(Self-Attention Mechanism)
自注意力机制(Self-Attention Mechanism)是一种在深度学习中广泛应用的技术,尤其在自然语言处理和计算机视觉等领域发挥了重要作用。
一、基本概念
自注意力机制主要是让模型能够根据输入数据的不同部分之间的关系,自动地为不同部分分配不同的注意力权重。它可以捕捉输入数据中的长距离依赖关系,而不需要依赖传统的顺序处理方式。
例如,在处理一个句子时,自注意力机制可以让模型根据句子中各个单词之间的关系,确定每个单词的重要程度,从而更好地理解句子的含义。
二、工作原理
计算相似度
- 对于给定的输入序列(如一个句子中的单词向量序列),首先计算每个元素(如单词向量)与其他元素之间的相似度。
- 常用的计算相似度的方法是点积(dot product)或缩放点积(scaled dot product)。
计算注意力权重
- 根据相似度计算结果,通过softmax函数将其转化为注意力权重。
- 注意力权重表示每个元素对其他元素的关注程度。
加权求和
- 最后,将每个元素与对应的注意力权重相乘,并进行求和,得到自注意力机制的输出。
- 输出结果是一个新的向量序列,其中每个向量都融合了输入序列中其他元素的信息,并且根据注意力权重进行了加权。
三、优势
并行计算
- 自注意力机制可以并行地计算每个元素的注意力权重,不像传统的循环神经网络(RNN)需要按顺序处理输入数据,因此可以大大提高计算效率。
长距离依赖捕捉
- 能够有效地捕捉输入数据中的长距离依赖关系,这对于处理长文本或复杂的图像等数据非常重要。
灵活性
- 可以很容易地与其他深度学习模型结合使用,如卷积神经网络(CNN)和循环神经网络,以提高模型的性能。
四、应用领域
自然语言处理
- 机器翻译:帮助模型更好地理解源语言和目标语言之间的关系,提高翻译质量。
- 文本分类:聚焦于文本中的关键信息,提高分类准确性。
- 阅读理解:分析文章中的不同部分,更准确地找到答案。
计算机视觉
- 图像分类:关注图像中的关键区域,提高分类准确性。
- 目标检测:确定图像中不同区域对于检测目标的重要性。
- 图像描述生成:根据图像的不同部分生成更准确的描述。
消融研究(Ablation Study)
消融研究(Ablation Study)是一种在科学研究,特别是在机器学习和计算机科学领域中常用的实验方法。
一、目的
其主要目的是为了理解一个复杂系统中各个组成部分的贡献和重要性。通过逐步去除或修改系统中的特定部分,观察系统性能的变化,从而确定每个部分对整体性能的影响。
二、具体做法
- 确定研究对象:首先明确要进行消融研究的复杂系统,例如一个深度学习模型、一个算法流程等。
- 选择要消融的部分:确定系统中的哪些组成部分将被逐个去除或修改。这些部分可以是模型的特定模块、算法的某个步骤、特定的特征等。
- 进行实验:分别对完整系统和去除特定部分后的系统进行实验。在机器学习中,通常使用相同的数据集和评估指标来比较性能变化。
- 分析结果:观察去除不同部分后系统性能的变化,例如准确率、召回率、F1 分数等指标的变化。通过分析这些结果,可以确定每个部分对整体性能的贡献程度。
三、举例
例如在一个图像分类的深度学习模型中,可能包括卷积层、池化层、全连接层等多个模块。为了研究每个模块的重要性,可以进行消融研究:
- 保留完整模型进行实验,得到基准性能。
- 去除卷积层,观察模型性能的变化,确定卷积层对图像特征提取的贡献。
- 去除池化层,观察性能变化,了解池化层在降低数据维度和提高模型鲁棒性方面的作用。
- 去除全连接层,分析其对最终分类结果的影响。
通过这样的消融研究,可以深入了解模型中各个模块的功能和重要性,为进一步改进和优化模型提供依据。
对比学习(Contrastive Learning)
对比学习(Contrastive Learning)是一种无监督学习方法,旨在通过学习数据的相似性和差异性来提取有效的特征表示。
一、基本原理
对比学习的核心思想是让模型学习如何区分相似的样本对和不相似的样本对。具体来说,它通过构建正负样本对,并让模型学习使得相似样本对之间的距离尽可能小,不相似样本对之间的距离尽可能大。
例如,对于图像数据,可以通过对同一图像进行不同的数据增强操作(如旋转、裁剪、颜色变换等)来生成正样本对,而不同的图像则构成负样本对。模型通过学习区分这些样本对,从而提取出能够反映图像本质特征的表示。
二、方法流程
- 数据准备
- 收集大量未标注的数据,并进行适当的数据增强操作以生成正样本对和负样本对。
- 构建损失函数
- 设计一个对比损失函数,该函数通常基于样本对之间的距离度量。常见的对比损失函数有InfoNCE损失、Triplet损失等。
- 模型训练
- 使用对比损失函数对模型进行训练。在训练过程中,模型不断调整参数以最小化损失函数,使得相似样本对的表示更加接近,不相似样本对的表示更加远离。
- 特征提取
- 训练完成后,可以使用模型提取数据的特征表示。这些特征表示通常具有较好的区分性和鲁棒性,可以用于后续的任务,如分类、聚类等。
三、优势
- 无需大量标注数据
- 对比学习是一种无监督学习方法,因此可以在没有大量标注数据的情况下进行训练,节省了标注数据的成本和时间。
- 学习到有效的特征表示
- 通过学习数据的相似性和差异性,对比学习可以提取出具有区分性和鲁棒性的特征表示,这些特征表示可以提高后续任务的性能。
- 可扩展性强
- 对比学习可以很容易地应用于不同类型的数据,如图像、文本、音频等,并且可以与其他深度学习方法结合使用,具有很强的可扩展性。
四、应用场景
- 计算机视觉
- 在图像分类、目标检测、图像检索等任务中,对比学习可以用于预训练模型,提取有效的图像特征,提高模型的性能。
- 自然语言处理
- 在文本分类、情感分析、机器翻译等任务中,对比学习可以用于学习词向量或句子向量的表示,提高模型的语言理解能力。
- 推荐系统
- 在推荐系统中,对比学习可以用于学习用户和物品的特征表示,提高推荐的准确性和个性化程度。
预训练
预训练是一种在特定任务之前对模型进行初步训练的方法。以下是关于预训练的详细介绍:
一、定义与目的
预训练是利用大规模数据对模型进行无监督或自监督学习,使模型学习到通用的特征表示和模式。其主要目的是为了让模型在后续特定任务的训练中能够更快地收敛,并且提高模型的性能和泛化能力。
二、预训练的方式
无监督预训练:
- 这种方式通常利用大量未标注的数据,让模型学习数据的内在结构和模式。例如,自编码器通过学习将输入数据重构为输出数据,从而提取数据的特征表示。
- 语言模型预训练也是一种常见的无监督预训练方法。通过预测句子中的下一个单词或掩码位置的单词,模型可以学习到语言的语法、语义和上下文信息。
自监督预训练:
- 自监督学习任务通常是通过从数据本身自动生成监督信号来进行训练。例如,在图像领域,可以通过对图像进行随机裁剪、旋转或颜色变换等操作,然后让模型预测原始图像的特征,从而进行自监督预训练。
三、预训练的优势
- 利用大规模数据:预训练可以利用大量的无标注数据,这些数据在现实中往往比较容易获取。相比之下,标注数据通常需要耗费大量的时间和人力成本。
- 通用特征表示:通过预训练,模型可以学习到通用的特征表示,这些特征可以在不同的任务中共享。这样可以减少在特定任务中对标注数据的需求,并且提高模型的泛化能力。
- 加速训练过程:由于预训练已经学习到了一些通用的特征和模式,在后续特定任务的训练中,模型可以更快地收敛,从而减少训练时间和计算资源的消耗。
四、预训练的应用领域
- 自然语言处理:在自然语言处理领域,预训练语言模型如 BERT、GPT 等已经取得了巨大的成功。这些模型在大规模文本数据上进行预训练,然后可以在各种自然语言处理任务中进行微调,如文本分类、命名实体识别、机器翻译等。
- 计算机视觉:在计算机视觉领域,预训练模型也被广泛应用。例如,在图像分类任务中,可以使用在大规模图像数据集上预训练的卷积神经网络模型,然后在特定的图像分类数据集上进行微调。
- 语音处理:预训练在语音处理领域也有应用。例如,可以使用在大规模语音数据集上预训练的声学模型和语言模型,然后在特定的语音识别或语音合成任务中进行微调。
总之,预训练是一种有效的模型训练方法,可以利用大规模数据学习通用的特征表示,提高模型的性能和泛化能力,并且加速训练过程。在各个领域中,预训练模型已经成为了一种重要的技术手段。
以下是一些预训练的例子:
一、自然语言处理领域
BERT(Bidirectional Encoder Representations from Transformers):
- BERT 由 Google 提出,在大规模文本语料库上进行无监督预训练。它通过掩码语言模型(Masked Language Model,MLM)和下一句预测(Next Sentence Prediction,NSP)两个任务进行预训练。
- 掩码语言模型随机掩盖输入文本中的一些单词,然后让模型预测被掩盖的单词。下一句预测任务则判断两个句子在原文中是否连续出现。
- BERT 在预训练后,可以在各种自然语言处理任务上进行微调,如文本分类、命名实体识别、问答系统等,取得了非常好的效果。
GPT(Generative Pretrained Transformer)系列:
- OpenAI 推出的 GPT 系列模型,包括 GPT、GPT-2、GPT-3 等。这些模型采用无监督的语言模型预训练方法,即通过预测下一个单词来学习语言的统计规律和语义信息。
- GPT-3 是目前最大的语言模型之一,拥有 1750 亿个参数。它在大量的文本数据上进行预训练,可以生成非常自然和流畅的文本,并且在各种自然语言处理任务上表现出色。
二、计算机视觉领域
ImageNet 预训练:
- 在计算机视觉领域,很多模型都是在 ImageNet 数据集上进行预训练。ImageNet 是一个大规模的图像分类数据集,包含超过 1400 万张图像和 2 万多个类别。
- 模型通常在 ImageNet 上进行有监督的预训练,即使用图像的类别标签进行训练。预训练后的模型可以作为特征提取器,在其他计算机视觉任务上进行微调,如目标检测、图像分割等。
自监督学习预训练:
- 近年来,自监督学习在计算机视觉领域也取得了很大的进展。例如,对比学习(Contrastive Learning)方法通过让模型学习区分正样本对和负样本对,从而学习到图像的特征表示。
- 一些著名的自监督学习方法包括 MoCo(Momentum Contrast)、SimCLR(Simple Framework for Contrastive Learning of Visual Representations)等。这些方法在大规模无标注图像数据集上进行预训练,可以学习到通用的图像特征表示,并且在下游任务上取得了很好的效果。
三、语音处理领域
wav2vec 系列:
- Facebook AI 提出的 wav2vec 系列模型采用自监督学习方法在大规模语音数据集上进行预训练。
- wav2vec 2.0 通过预测被掩盖的音频片段来学习语音的特征表示。预训练后的模型可以在语音识别、语音合成等任务上进行微调。
HuBERT(Hidden-Unit BERT):
- HuBERT 也是一种基于自监督学习的语音预训练模型。它通过对音频信号进行聚类,然后让模型预测音频片段所属的聚类类别来进行预训练。
- HuBERT 在语音处理任务上表现出了很高的性能,并且可以与其他语音处理技术相结合,提高语音处理系统的性能。
这些预训练模型在各自的领域中都取得了非常好的效果,并且为人工智能的发展做出了重要贡献。随着技术的不断进步,预训练方法也在不断发展和创新,未来将会有更多更强大的预训练模型出现。
以 BERT(Bidirectional Encoder Representations from Transformers)为例。
一、预训练数据
BERT 使用大规模的文本语料库进行预训练,例如维基百科、书籍等。这些文本数据涵盖了各种领域和主题,为模型提供了丰富的语言知识和模式。
二、预训练任务
掩码语言模型(Masked Language Model,MLM):
- 随机选择输入文本中的一些单词,将其替换为特殊的掩码标记 [MASK]。
- 模型的任务是根据上下文预测被掩码的单词。例如,对于句子“今天天气很[MASK]。”,模型需要预测出被掩码的单词“好”。
- 通过这种方式,模型学习到语言的上下文信息和语义表示。
下一句预测(Next Sentence Prediction,NSP):
- 给定两个句子 A 和 B,模型需要判断句子 B 是否是句子 A 的下一句。
- 例如,对于句子对“我喜欢吃苹果。”和“苹果是一种水果。”,模型应该判断出句子 B 是句子 A 的下一句;而对于句子对“我喜欢吃苹果。”和“我喜欢看电影。”,模型应该判断出句子 B 不是句子 A 的下一句。
- 这个任务帮助模型学习句子之间的关系和连贯性。
三、预训练过程
数据预处理:
- 对输入的文本进行清洗和预处理,包括去除特殊字符、转换为小写等。
- 将文本分割成单词或子词(subword),以便模型更好地处理不同长度的文本。
模型架构:
- BERT 使用 Transformer 架构,由多层编码器组成。
- 每个编码器层包含多头注意力机制(Multi-Head Attention)和前馈神经网络(Feed-Forward Neural Network)。
训练参数设置:
- 设置合适的学习率、批次大小、训练轮数等参数。
- 通常使用大规模的分布式训练,利用多块 GPU 或 TPU 加速训练过程。
优化算法:
- 使用优化算法如 Adam 来更新模型的参数,最小化预训练任务的损失函数。
持续训练:
- 模型在大规模数据上进行多轮训练,不断调整参数以提高在预训练任务上的性能。
- 监控训练过程中的损失值和评估指标,确保模型在训练过程中不断改进。
四、预训练结果
经过预训练后,BERT 学习到了通用的语言表示,可以在各种自然语言处理任务上进行微调。
例如,在文本分类任务中,只需要在预训练的 BERT 模型上添加一个分类层,并在特定的任务数据集上进行微调,就可以得到一个性能良好的文本分类模型。
(
这句话可以从以下几个方面来理解:
一、预训练模型的优势
- 通用语言表示:预训练的 BERT 模型在大规模文本数据上进行了无监督学习,已经学习到了通用的语言表示,包括语法、语义、上下文信息等。这种通用的语言表示可以为各种自然语言处理任务提供一个良好的起点。
- 特征提取能力:BERT 模型具有强大的特征提取能力,能够自动从文本中提取出有用的特征。这些特征可以帮助模型更好地理解文本的含义,从而提高文本分类的准确性。
二、添加分类层
- 特定任务适应:在预训练的 BERT 模型上添加一个分类层,是为了使模型能够适应特定的文本分类任务。分类层通常是一个全连接层,它将 BERT 模型提取的特征映射到不同的类别上。
- 学习任务相关信息:通过添加分类层,模型可以学习到与特定任务相关的信息,例如不同类别的特征、类别之间的关系等。这样可以使模型更加专注于特定的任务,提高分类的准确性。
三、微调过程
- 利用特定任务数据集:在特定的任务数据集上进行微调,是为了让模型进一步适应特定的任务和数据分布。特定任务数据集通常是标注好的文本数据,其中每个文本都被分配了一个类别标签。
- 调整模型参数:微调过程中,模型会根据特定任务数据集的损失函数来调整自身的参数。这个过程类似于在预训练模型的基础上进行有监督学习,使模型能够更好地拟合特定任务的数据。
- 提高性能:通过微调,模型可以利用预训练模型的通用语言表示和特征提取能力,同时学习到特定任务的相关信息,从而提高文本分类的性能。
四、总结
在文本分类任务中,使用预训练的 BERT 模型并添加分类层进行微调,可以充分利用预训练模型的优势,快速构建一个性能良好的文本分类模型。这种方法不仅可以节省大量的训练时间和计算资源,还可以提高模型的泛化能力和准确性。
)
总之,BERT 的预训练过程通过利用大规模文本数据和精心设计的预训练任务,使模型学习到丰富的语言知识和模式,为后续的特定任务应用提供了强大的基础。
Flash Attention
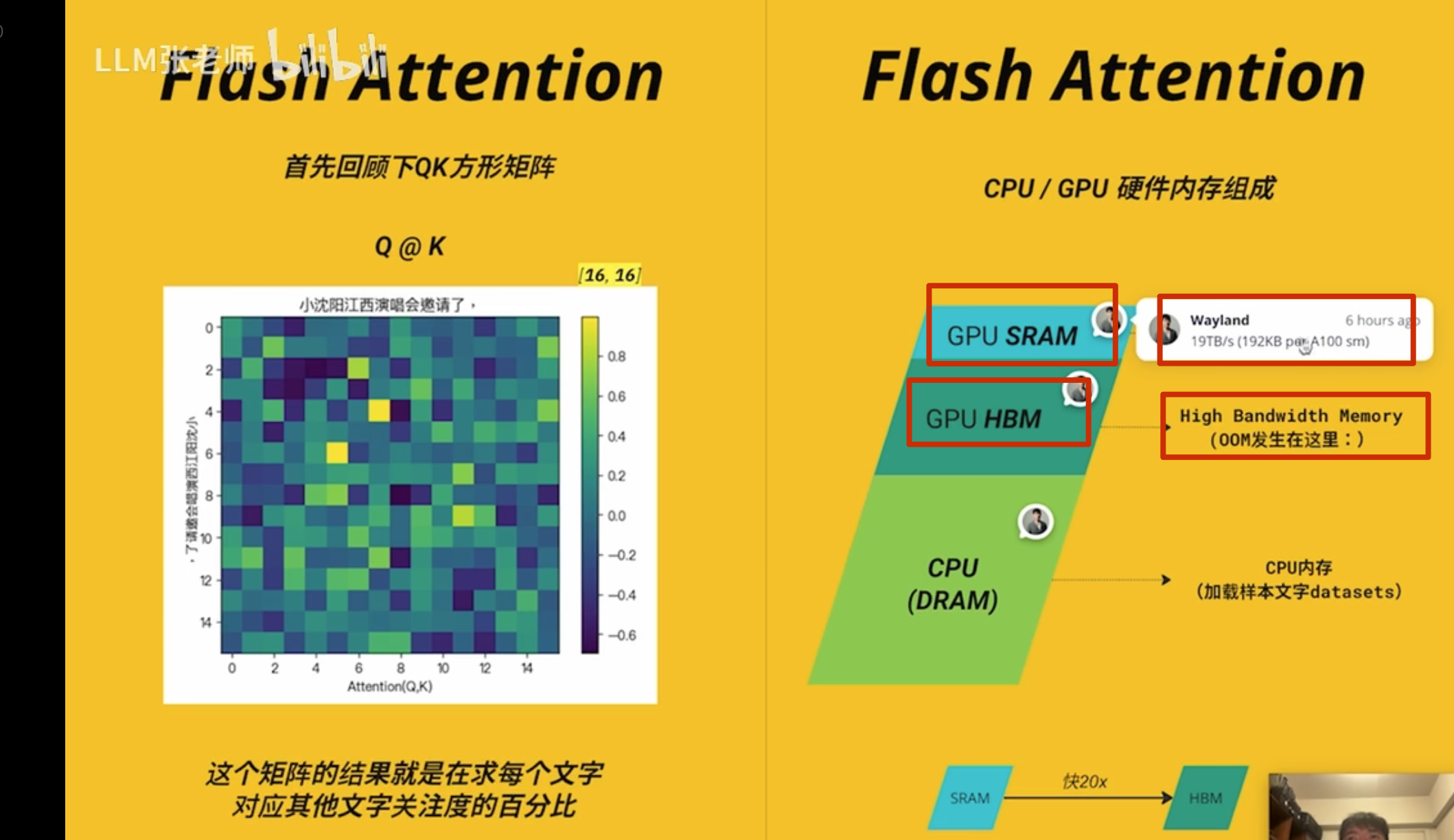
耗时分析
耗时的反而不是矩阵相乘
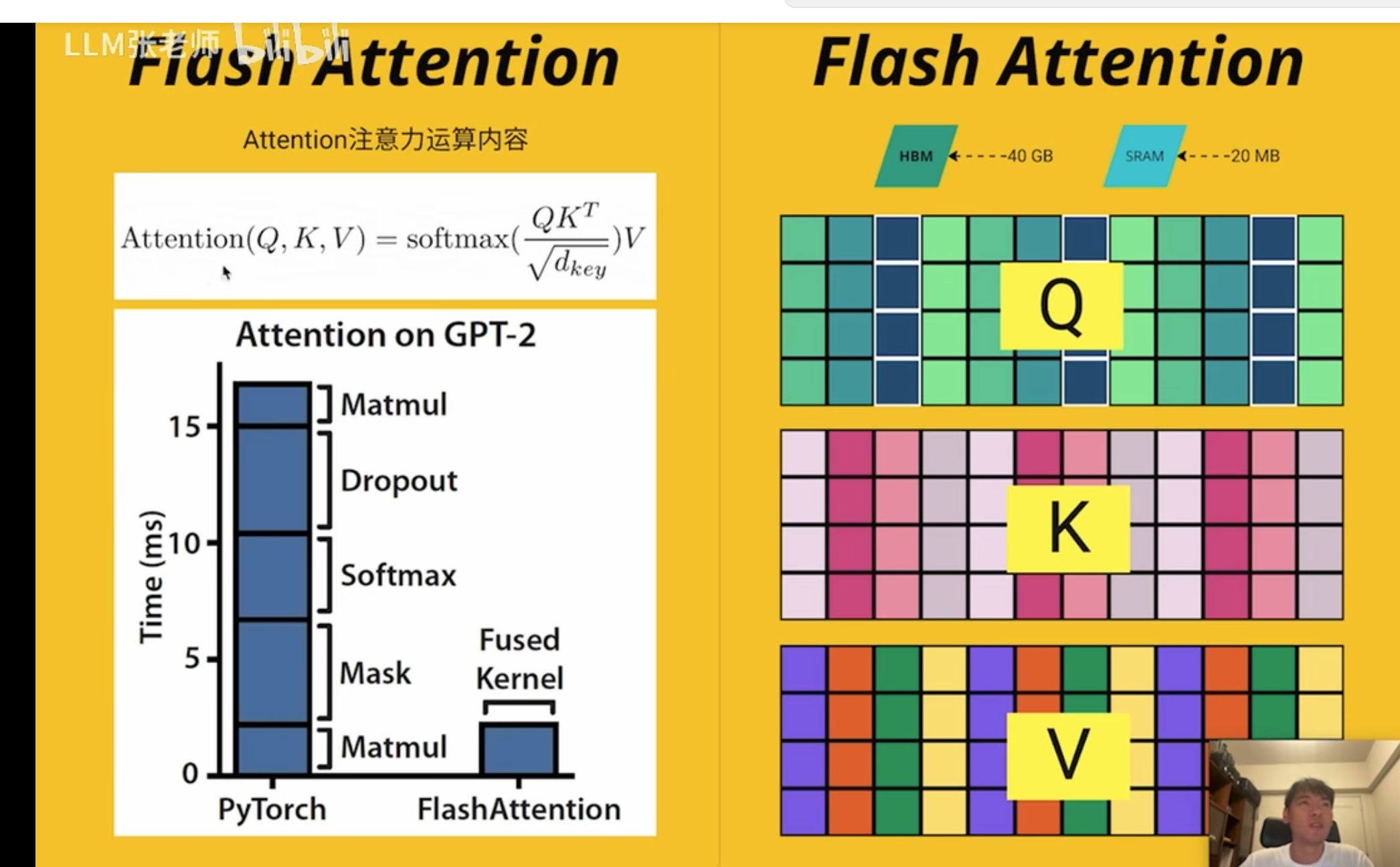
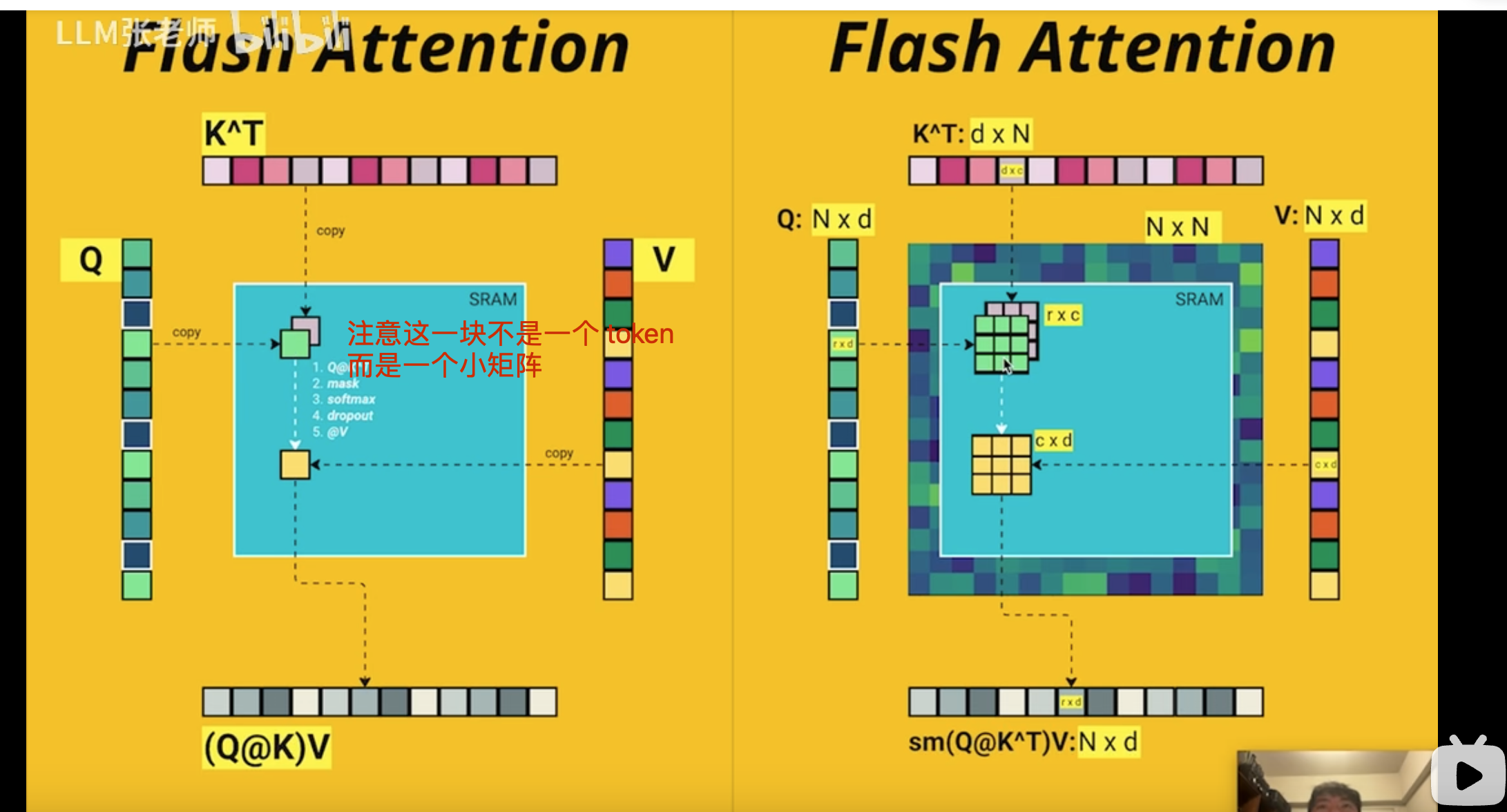
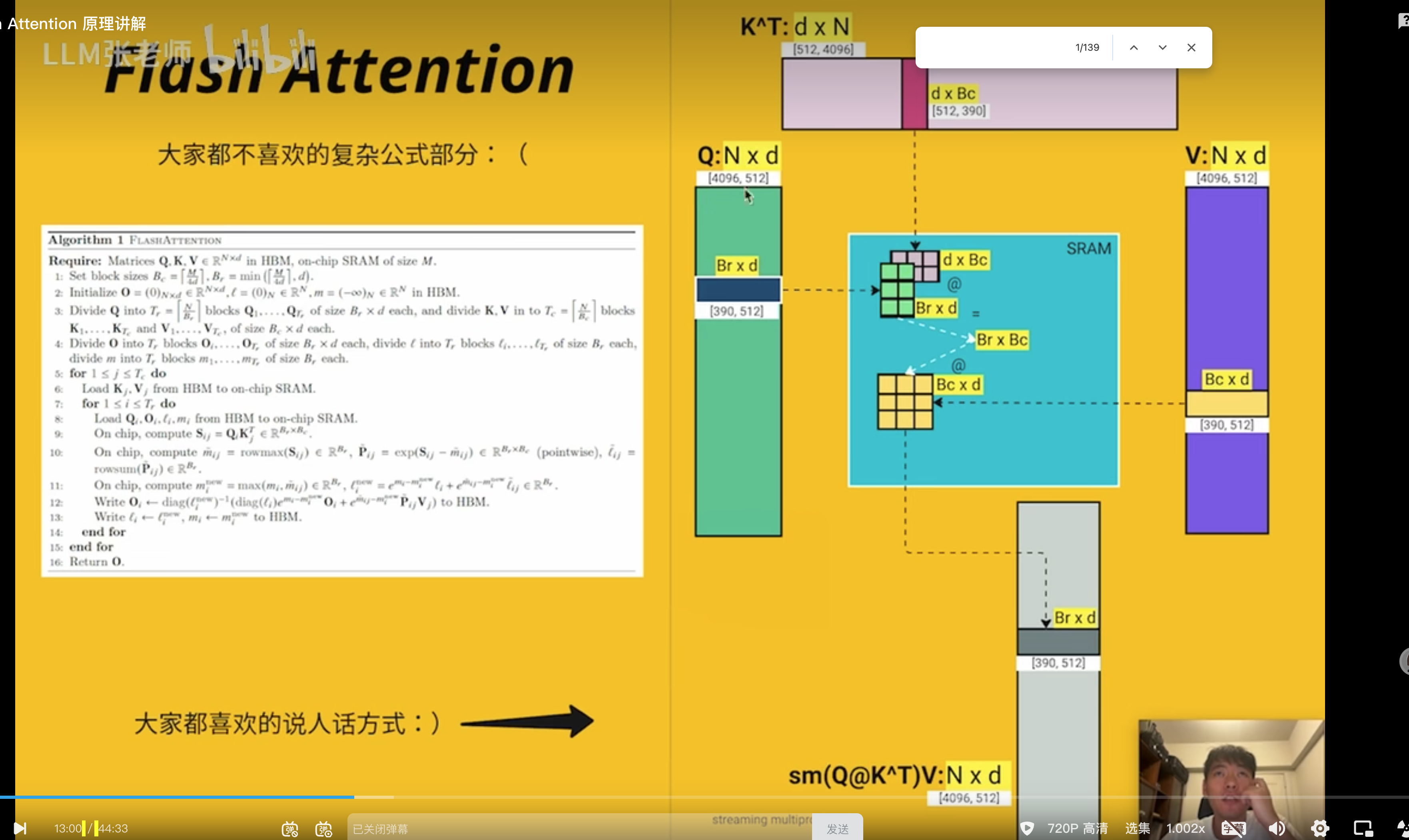
实际是多头和多批次的
A100 有 108 个

最难的是 softmax 运算这部分
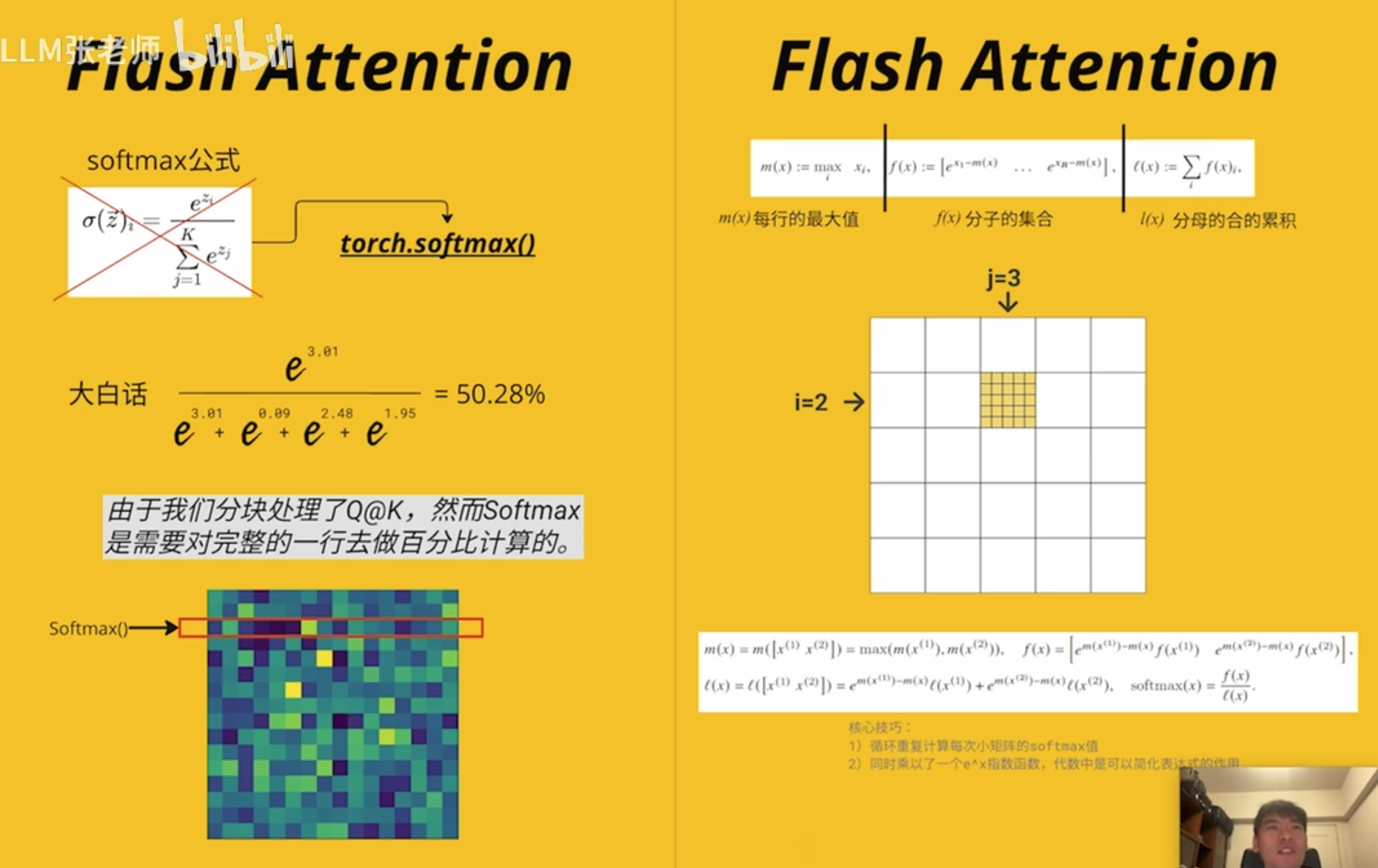

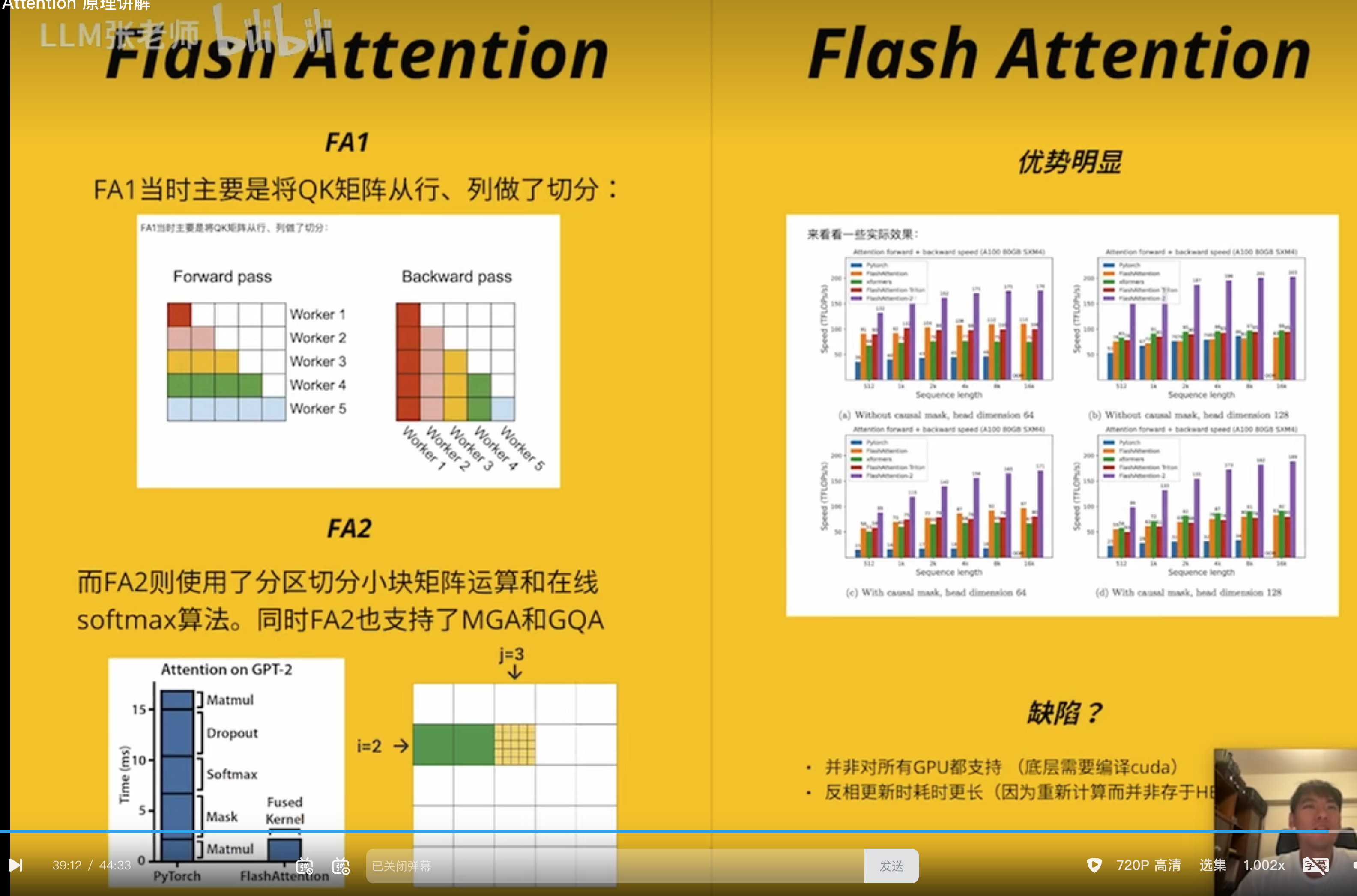

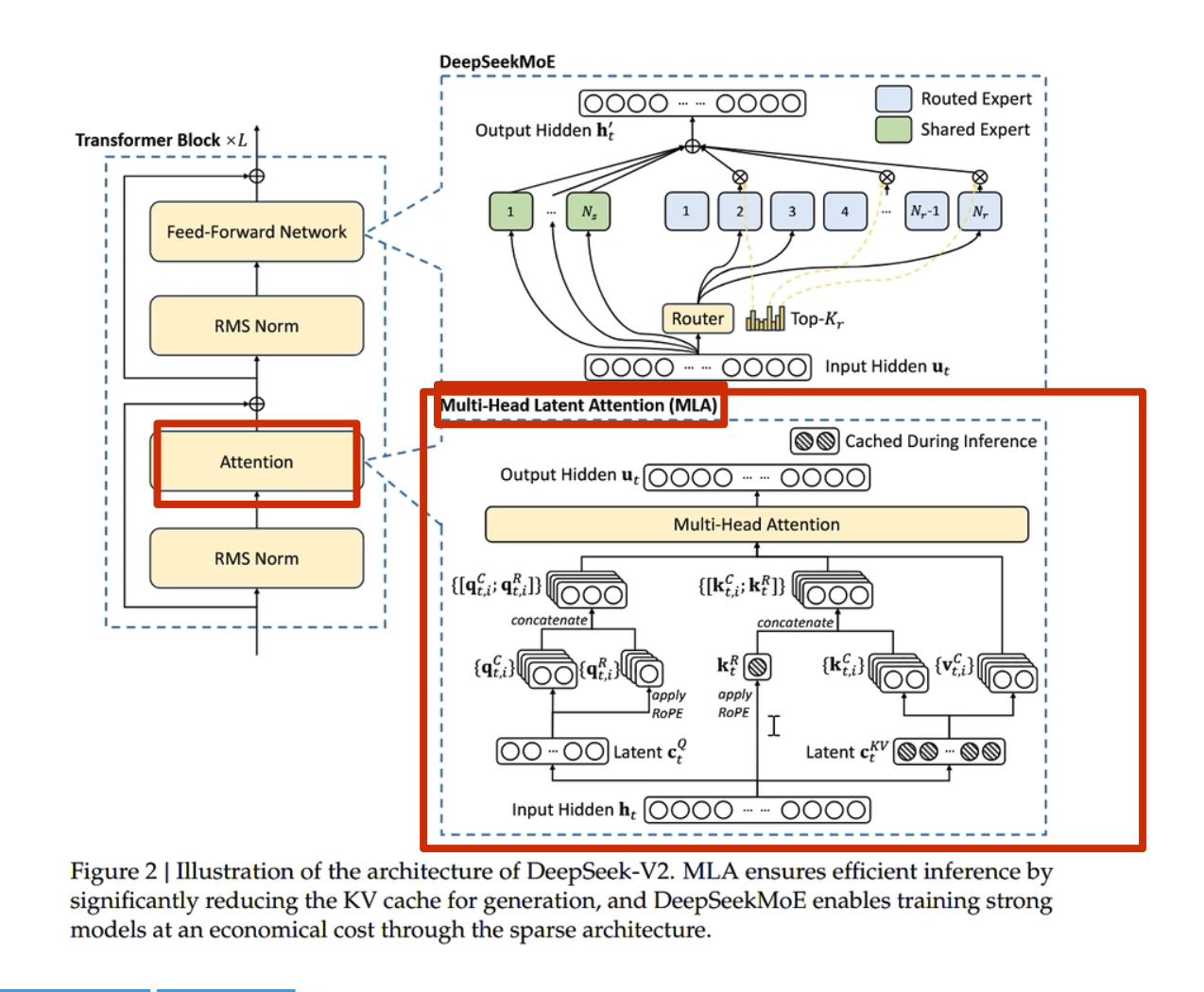
缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA

前几天,幻方发布的DeepSeek-V2引起了大家的热烈讨论。首先,最让人哗然的是1块钱100万token的价格,普遍比现有的各种竞品API便宜了两个数量级,以至于有人调侃“这个价格哪怕它输出乱码,我也会认为这个乱码是一种艺术”;其次,从模型的技术报告看,如此便宜的价格背后的关键技术之一是它新提出的MLA(Multi-head Latent Attention),这是对GQA的改进,据说能比GQA更省更好,也引起了读者的广泛关注。
接下来,本文将跟大家一起梳理一下从MHA、MQA、GQA到MLA的演变历程,并着重介绍一下MLA的设计思路。
MHA#

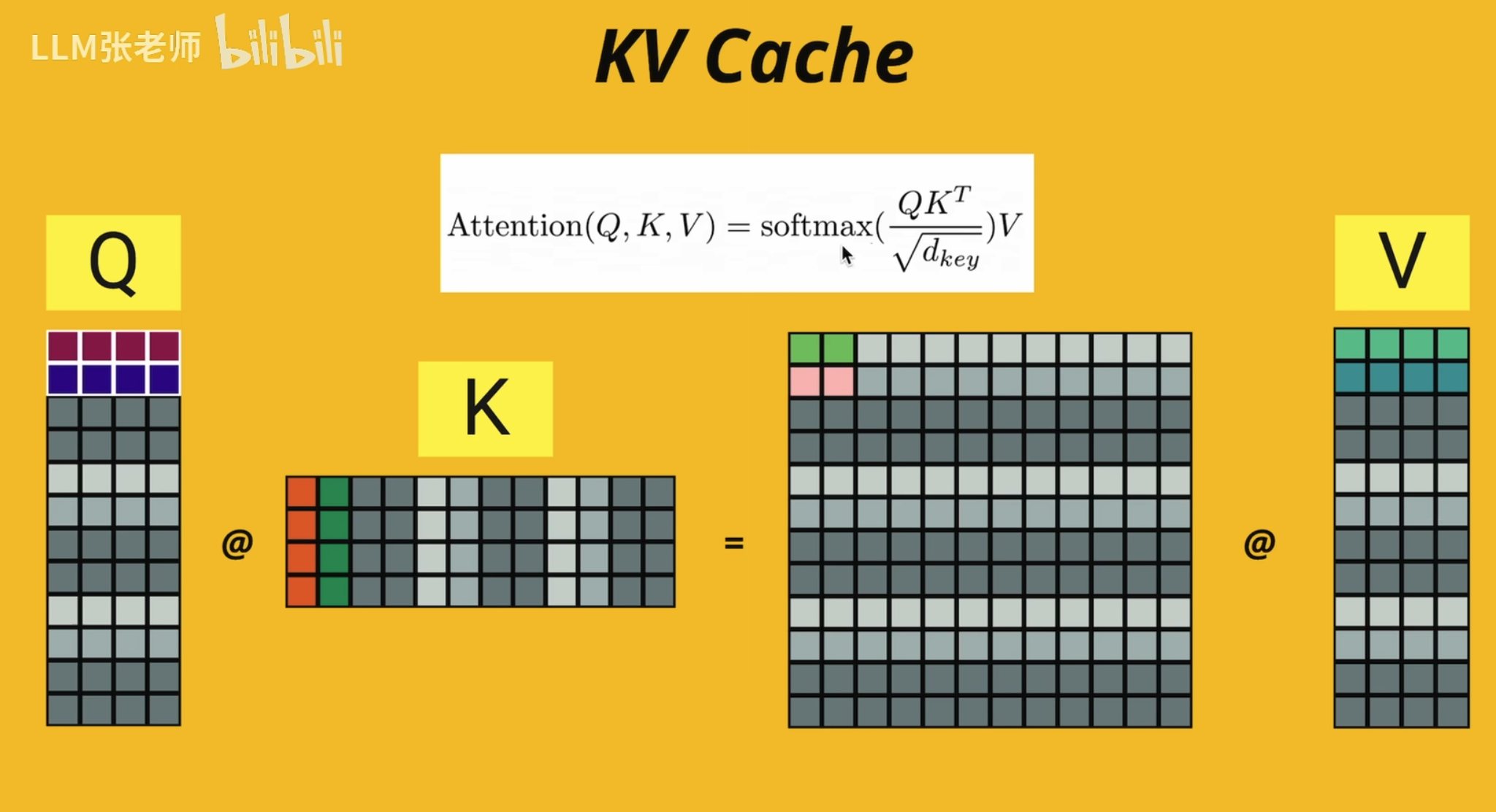
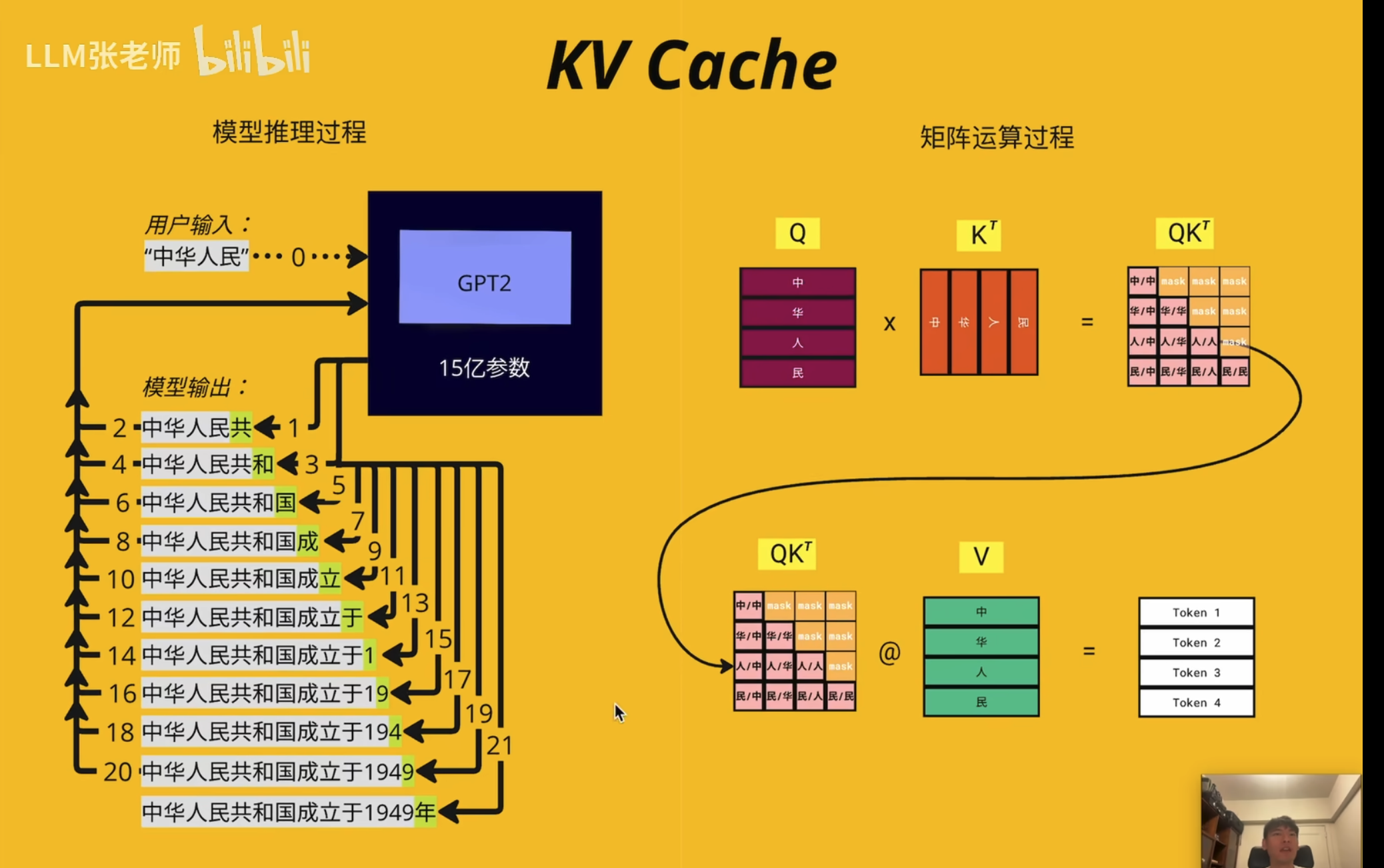
KV Cache(K-V Cache)

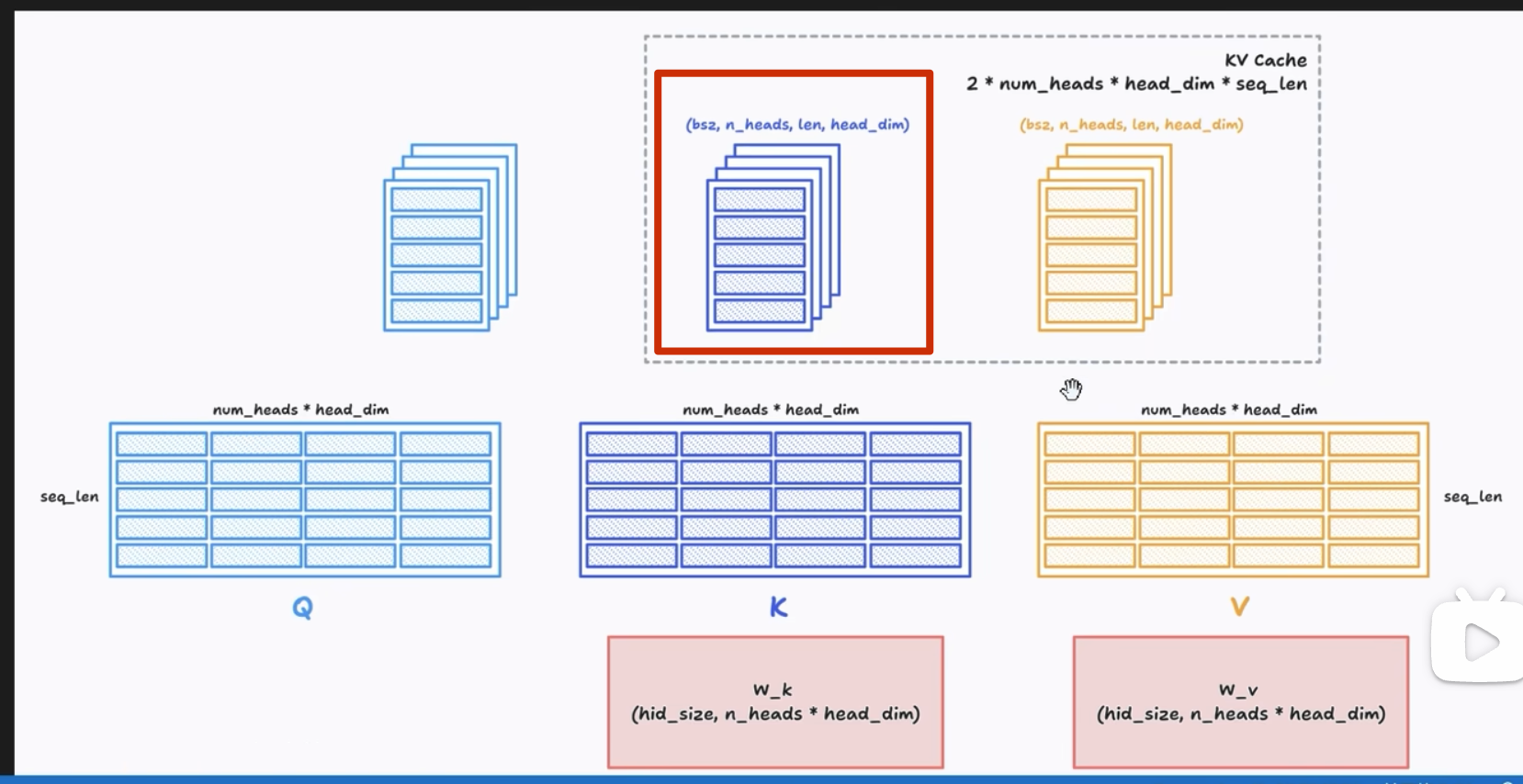
瓶颈

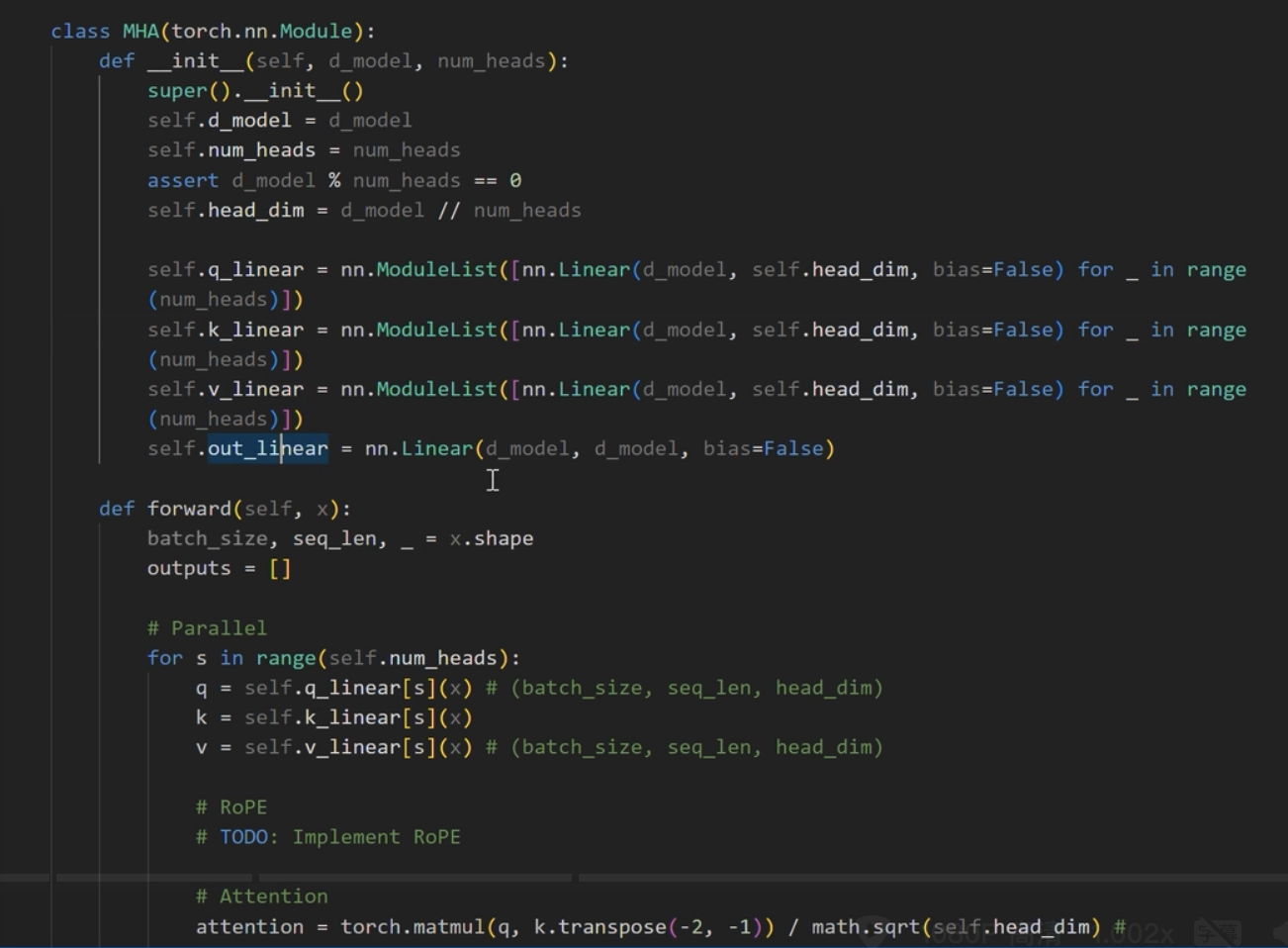
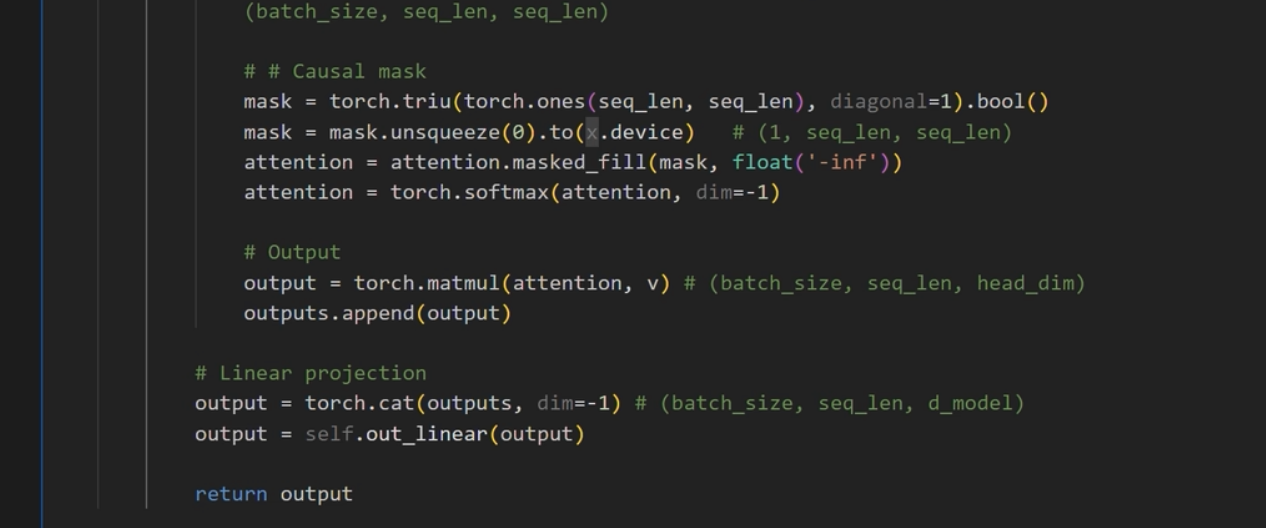
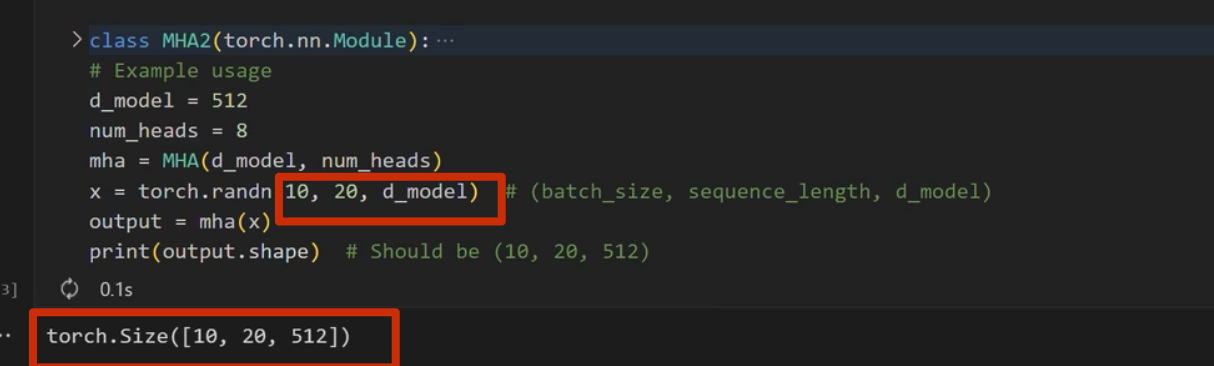
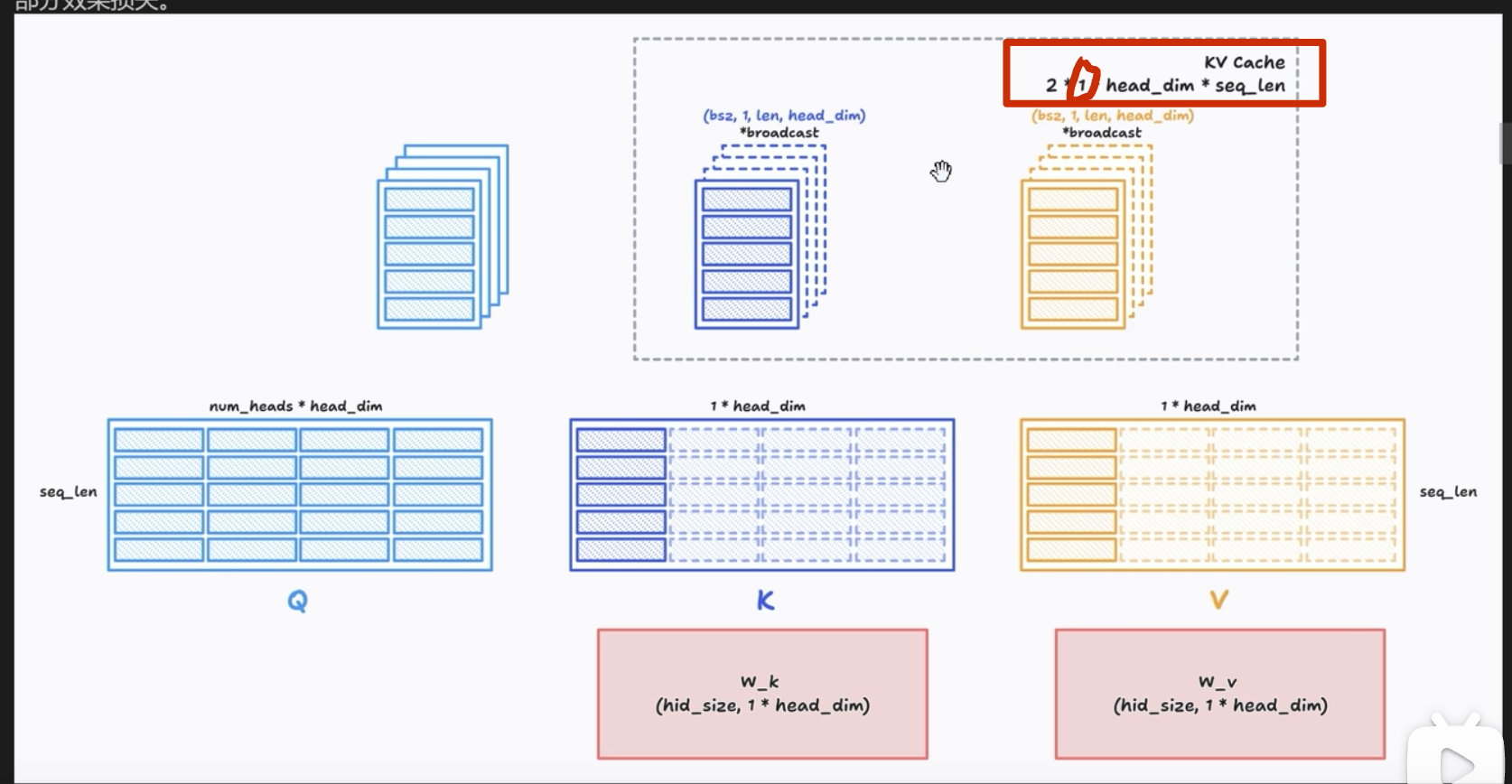
注意这里 d_model = head_dim* n_head

MQA

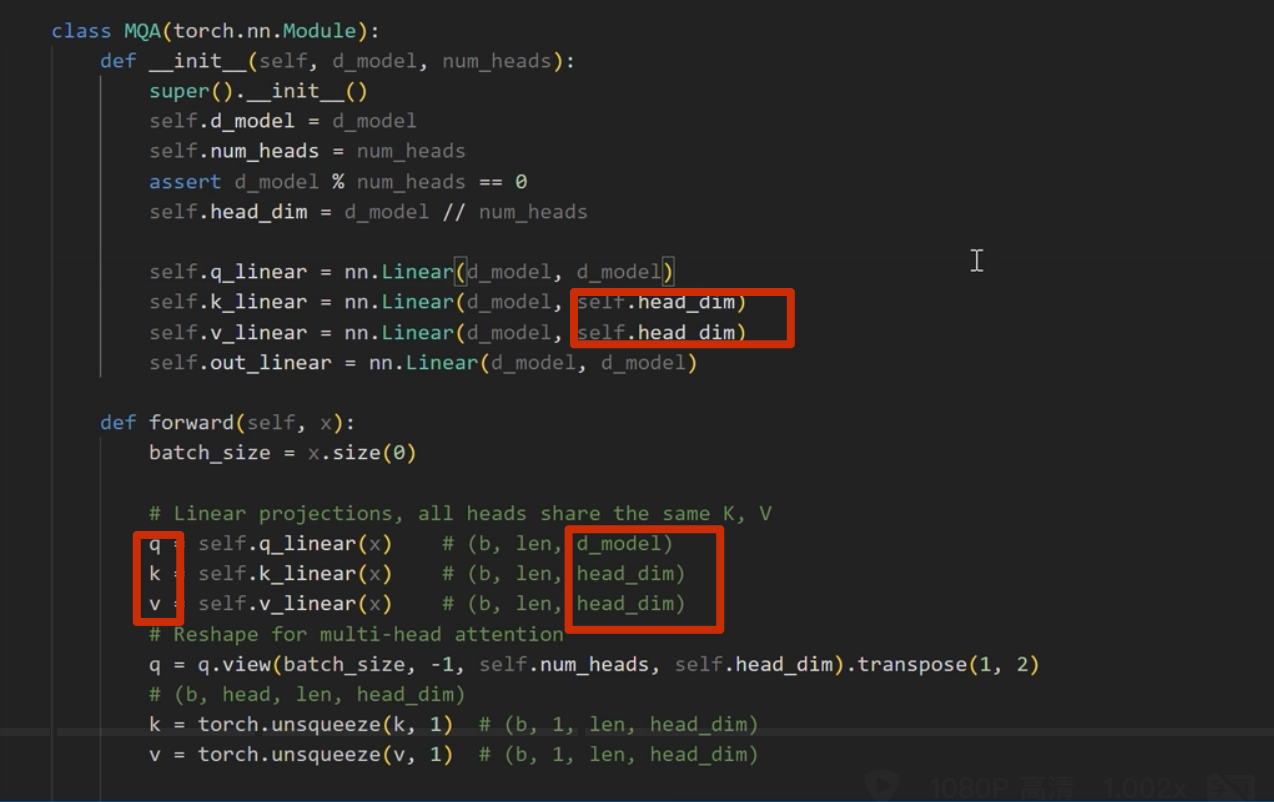
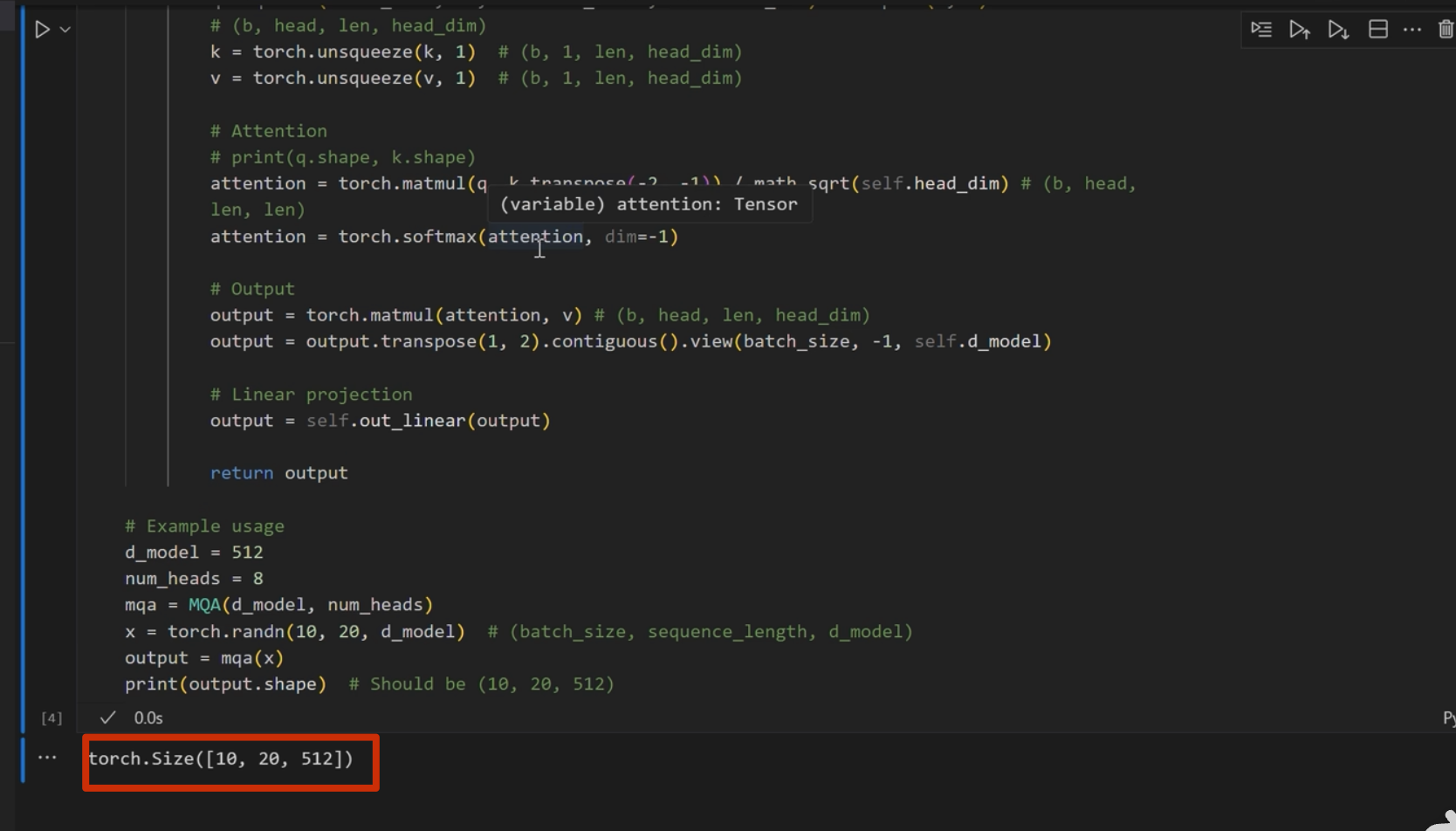
GQA

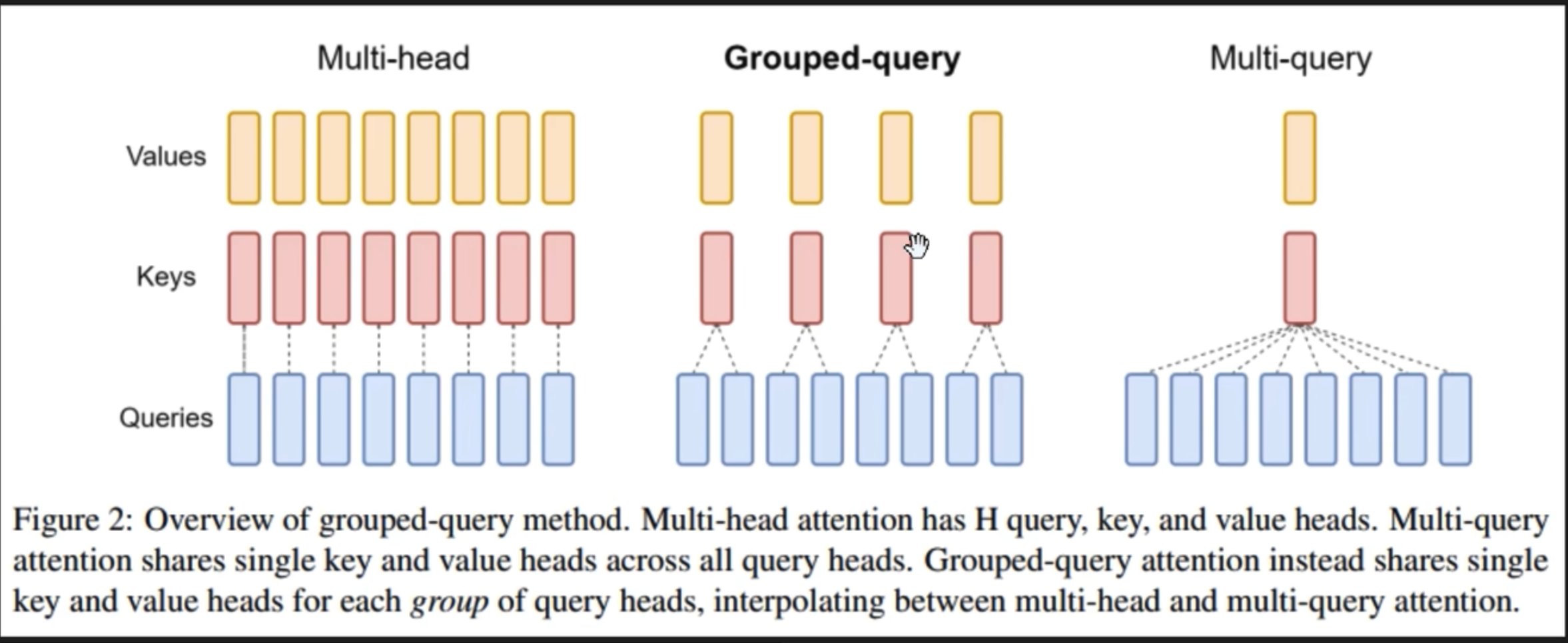
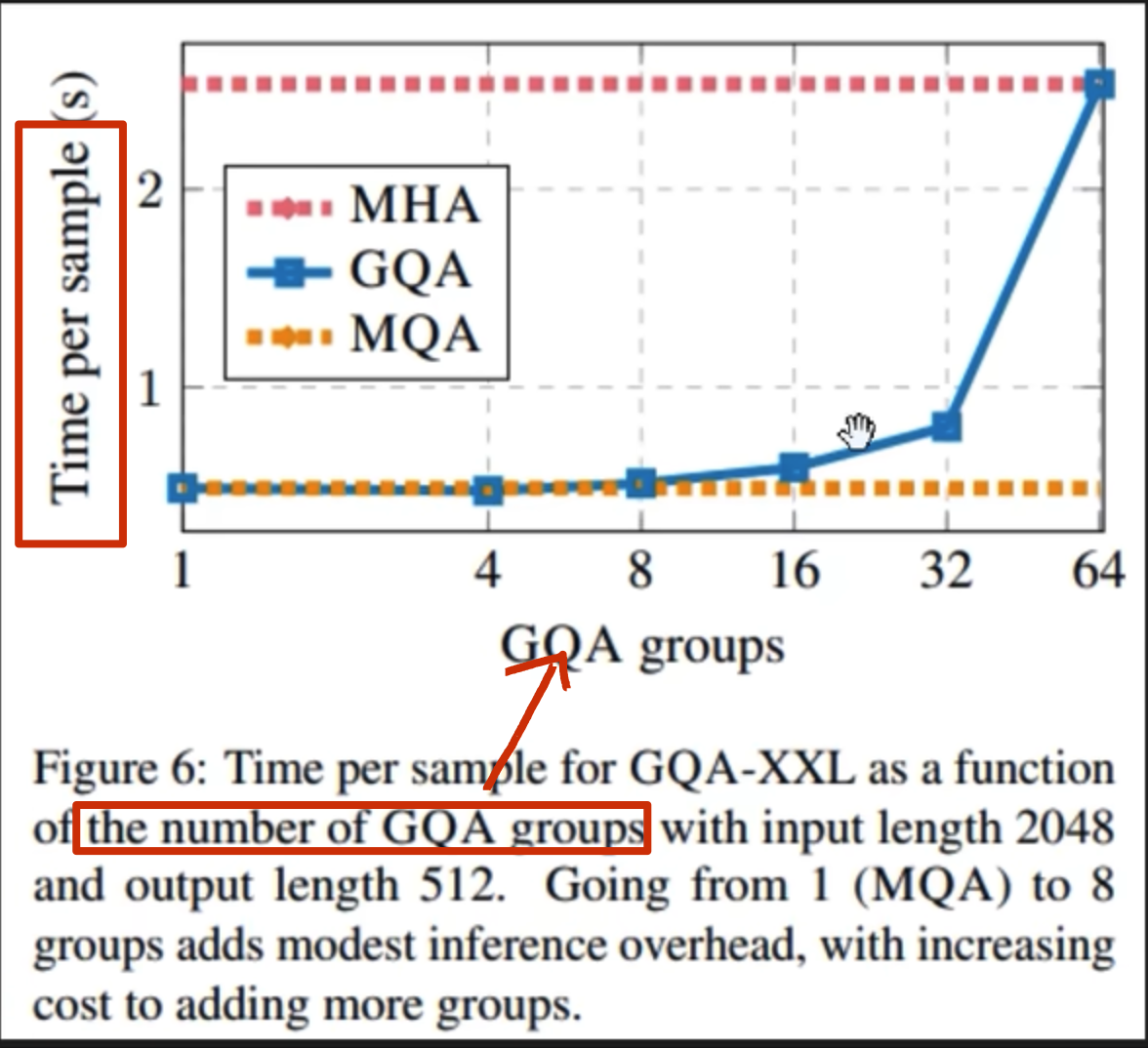
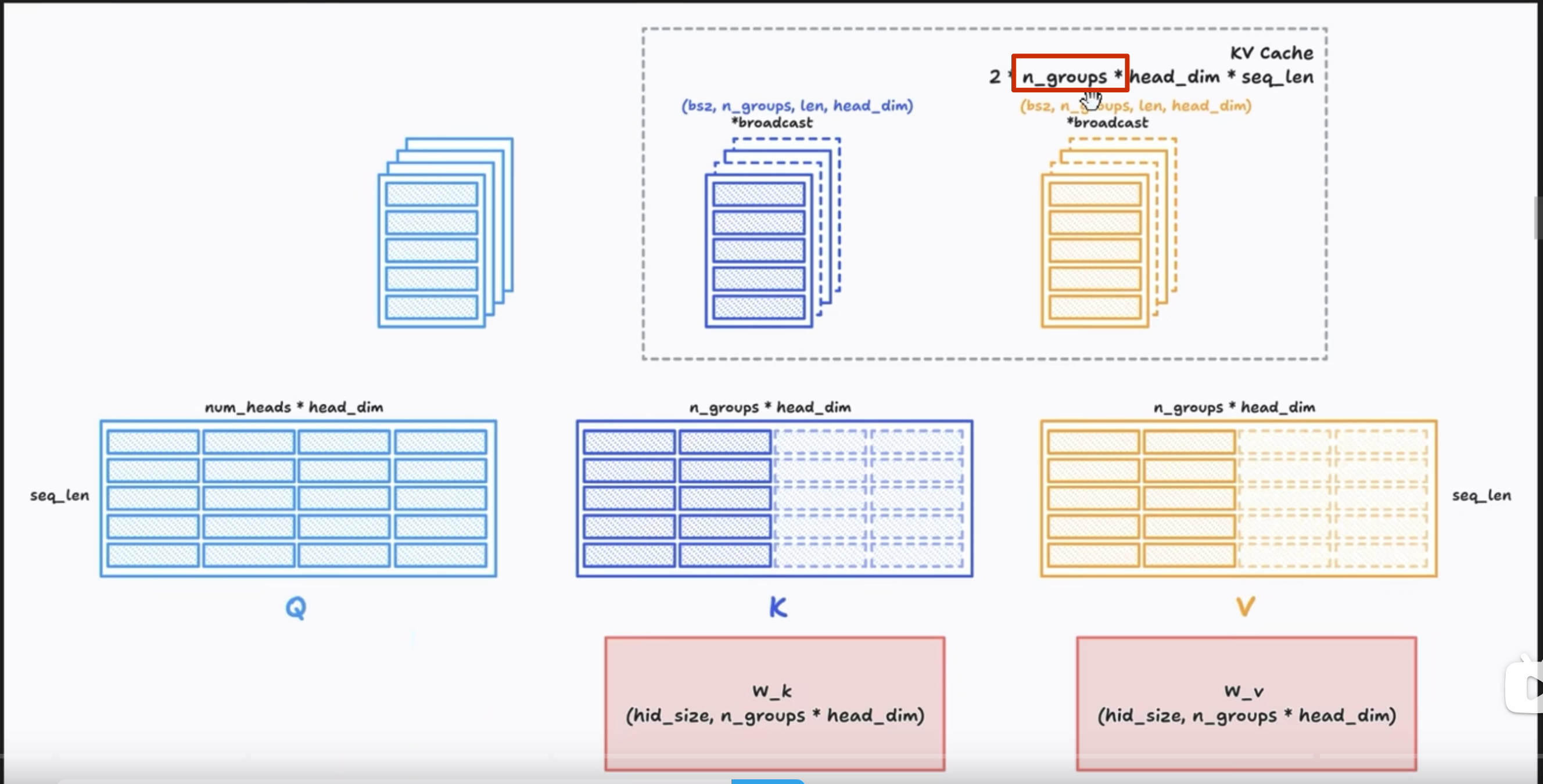
llama 代码如下:
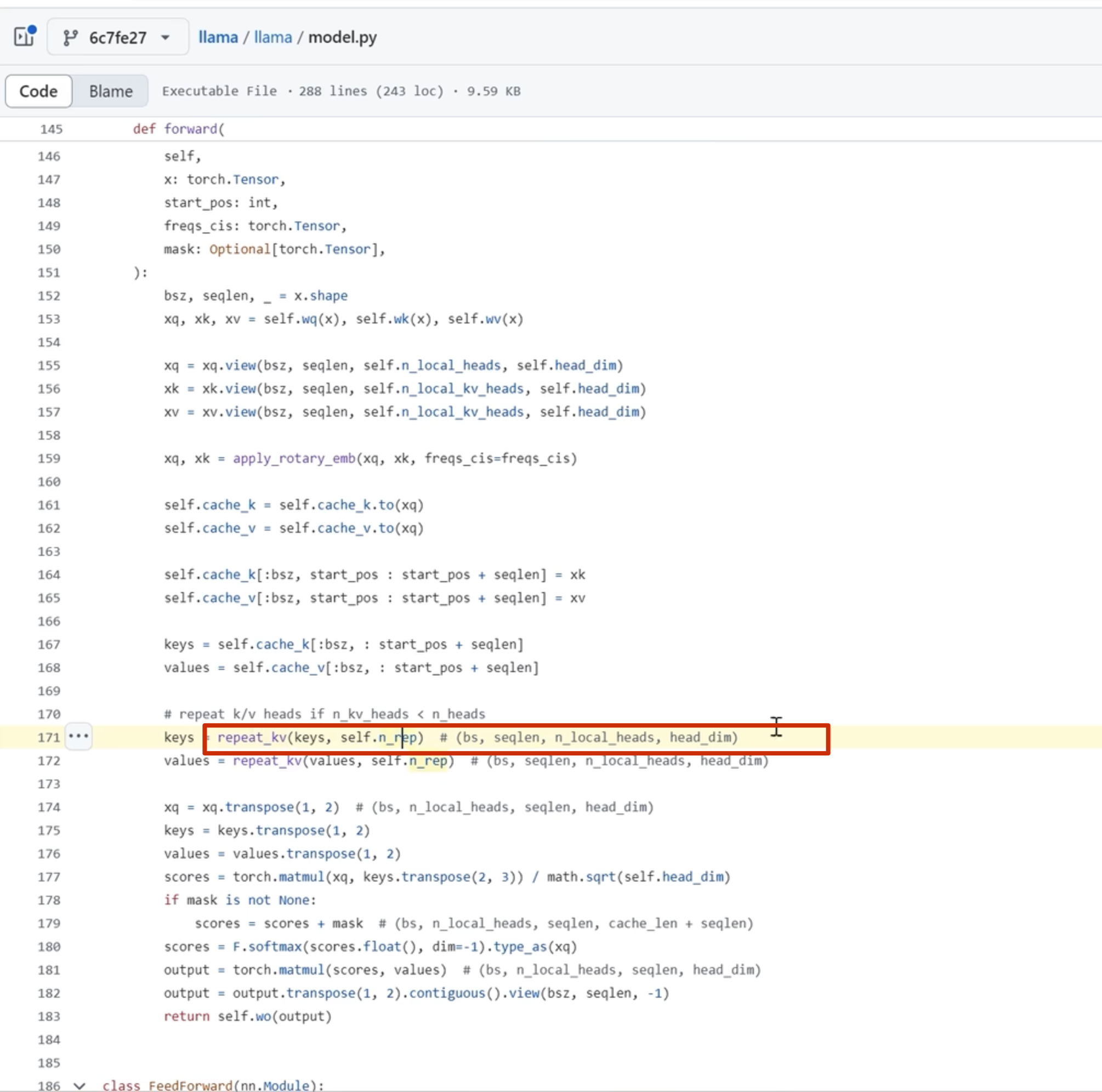
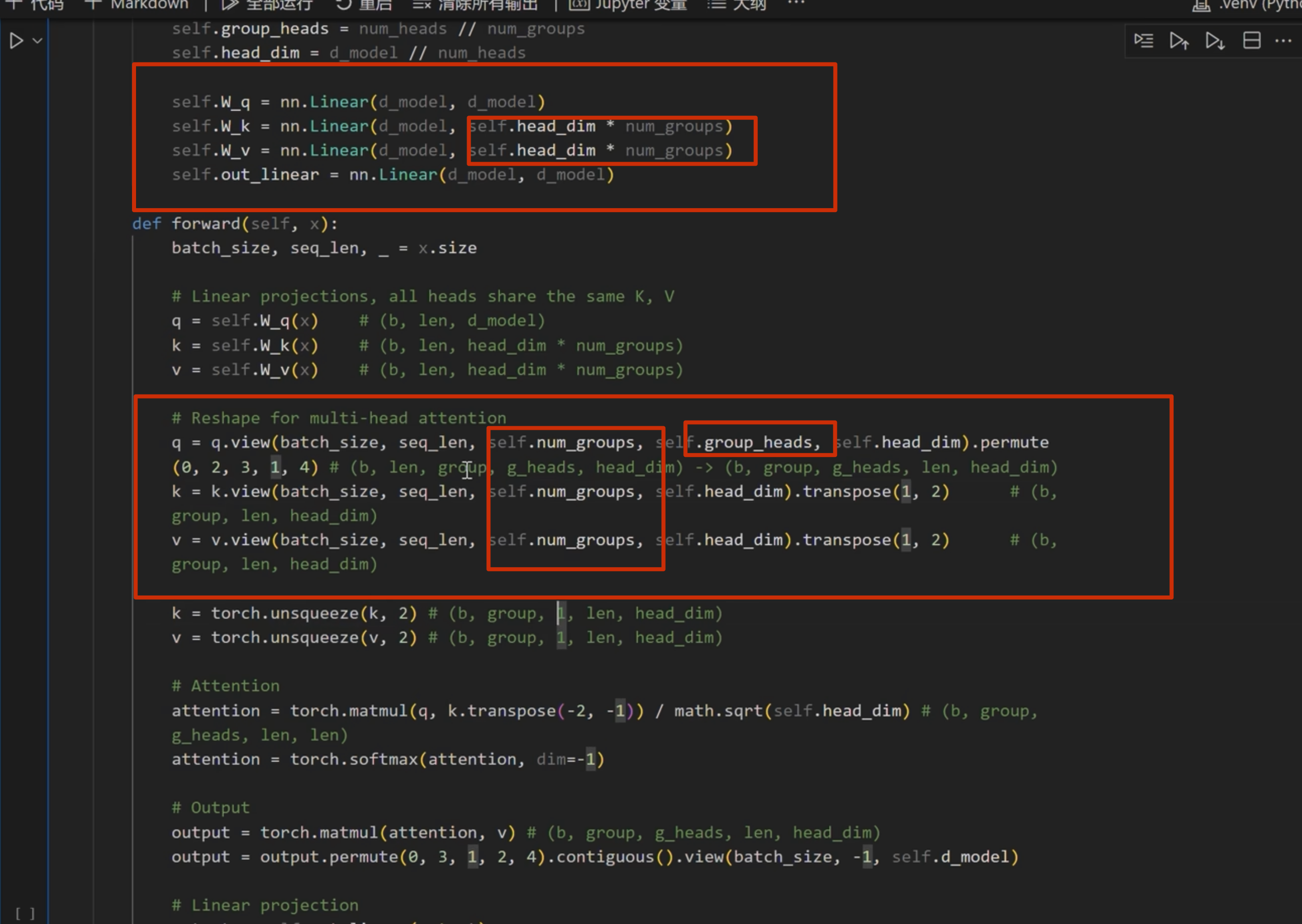
MLA
先看后面 Part1,2,3

(不理解,下面的当我乱说的,没看懂 g 是什么)
g= n_groups(下面说每一份被均分为 g 份),所以\(k_i\) =\([k_i^{(1)},k_i^{(2)}, ....,k_i^{(g)}]\),(\(k_i\)形状为1n_groups) 所以 c_i 为 1x (n_groups x head_dim x 2*)
x_i为 1xd, Wc为d x n_groups x 2 x head_dim
想说n_groups x 2 x head_dim一般小于 d??不一定吧,嘶 不应该相等吗?
Part1
投影后 对半分->复制(分割、复制)

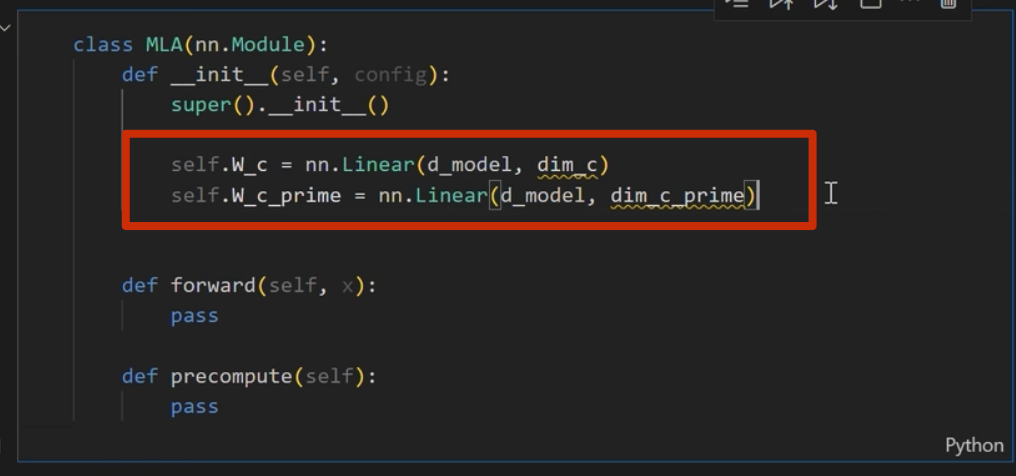
所以要求出上面圈出来的两个矩阵是关键



问题:

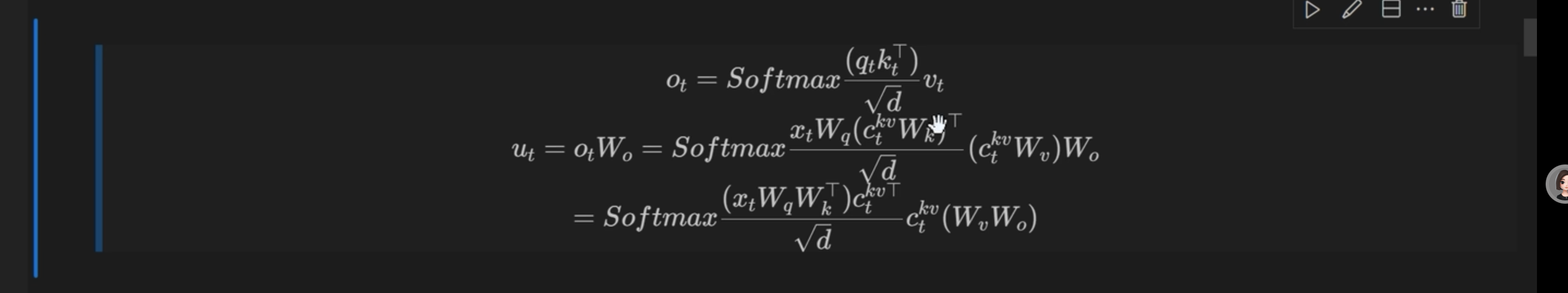

Part2(新问题,不兼容 RoPE(旋转位置编码 ,就是那个位置编码))






最后兼容 RoPE 的方案

Part3



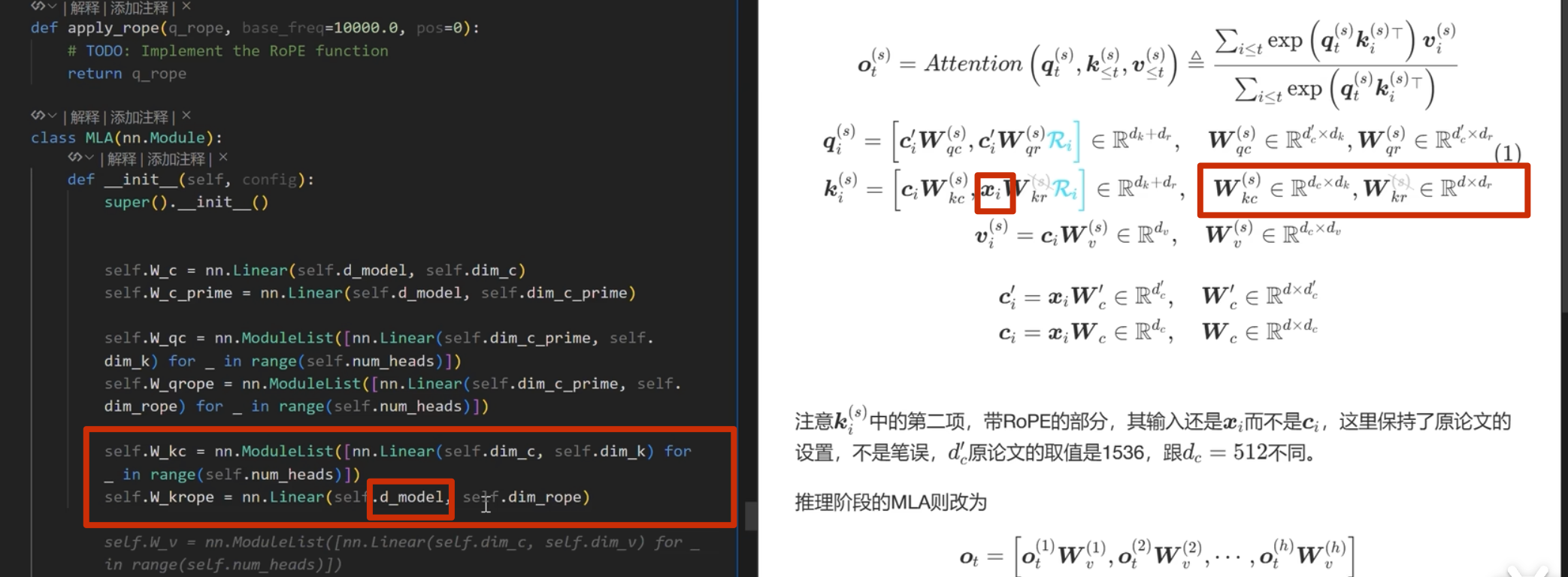
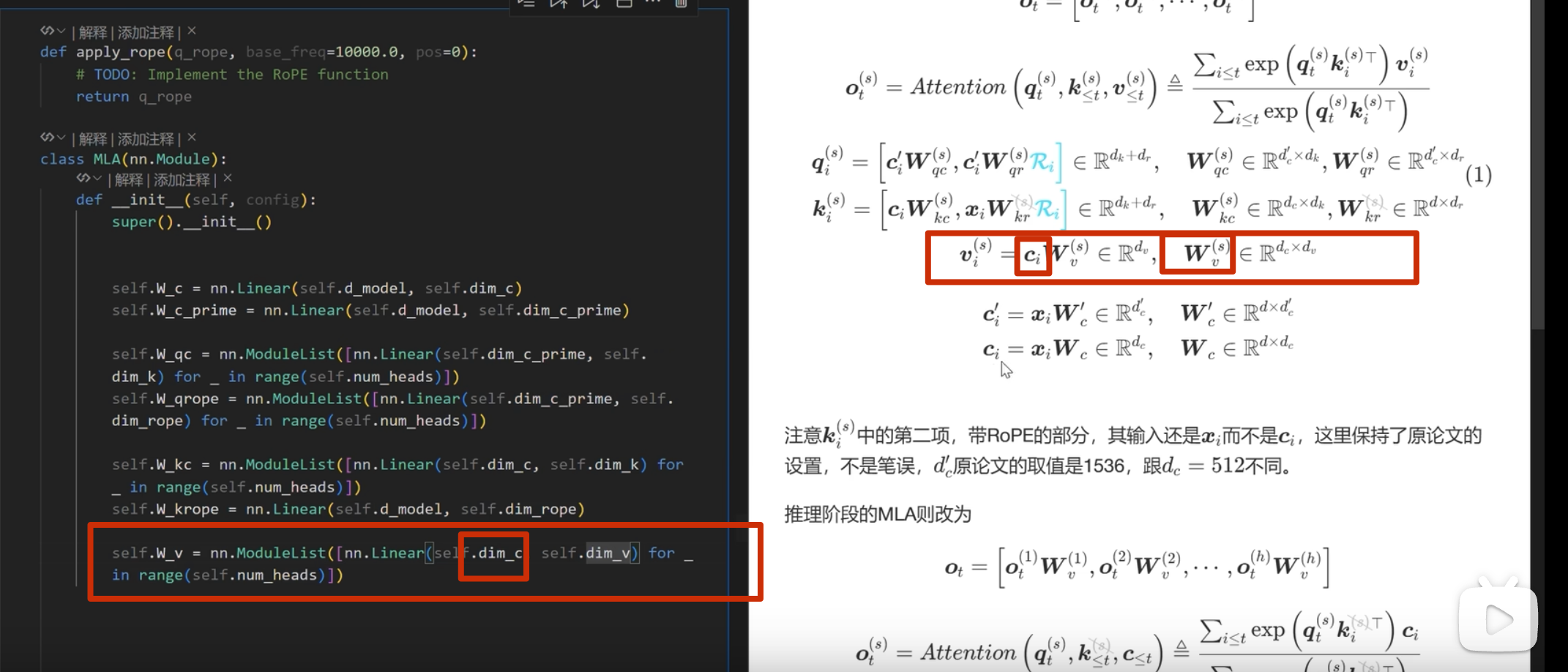
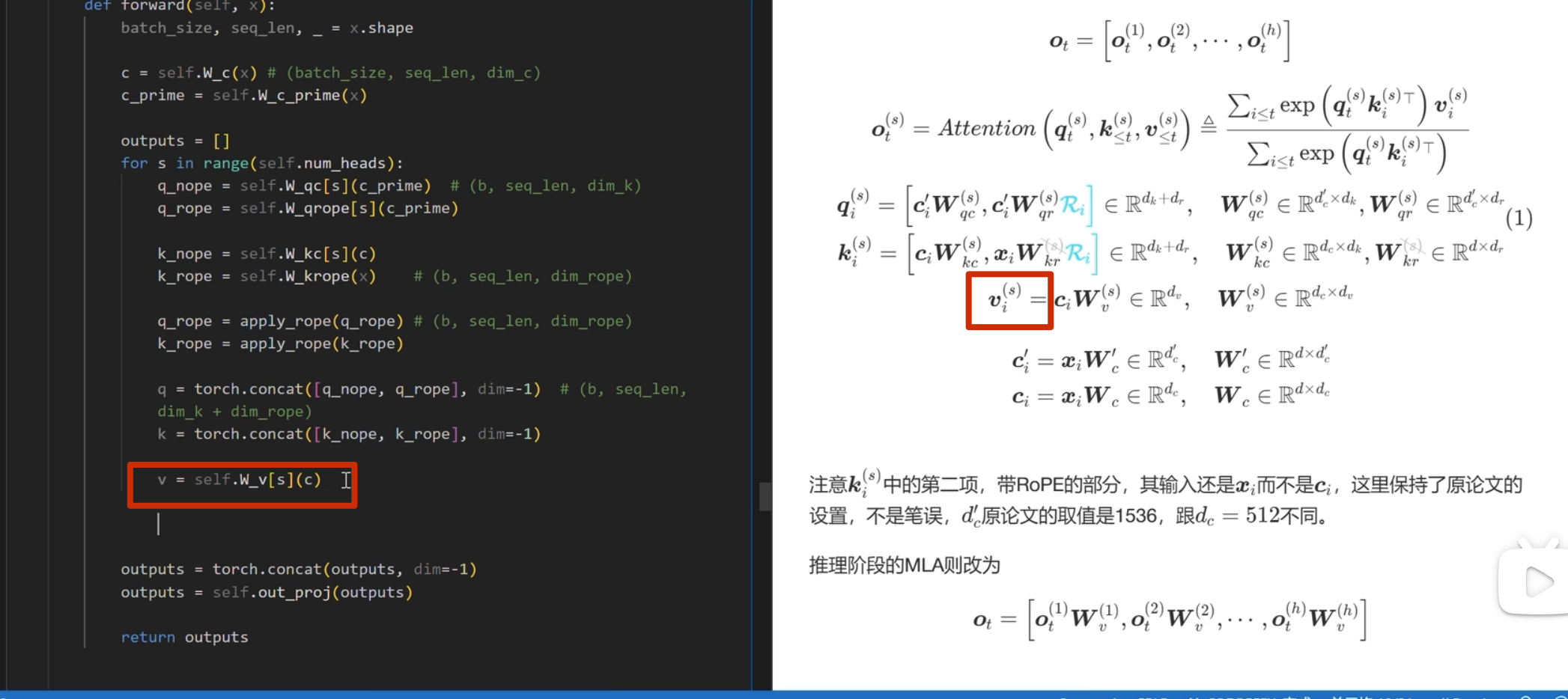
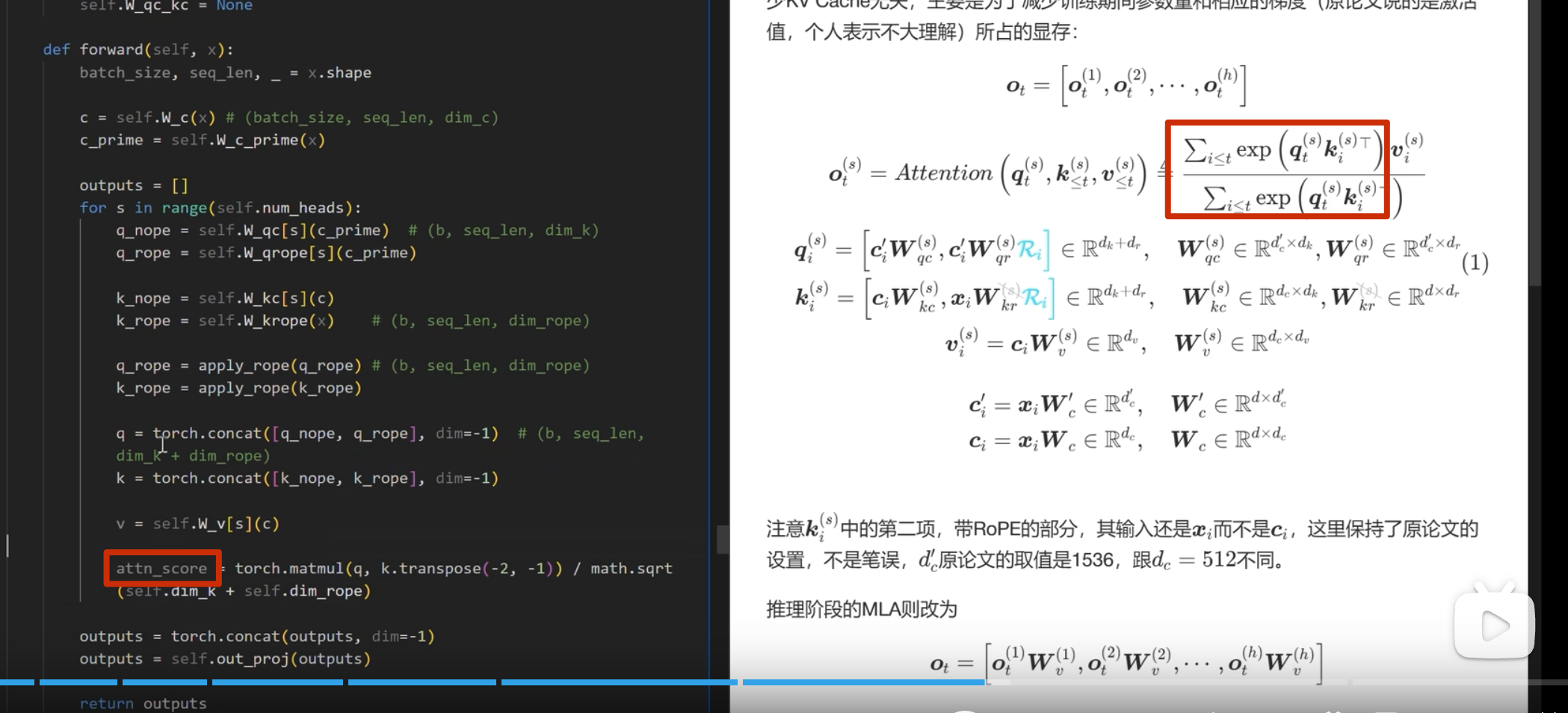
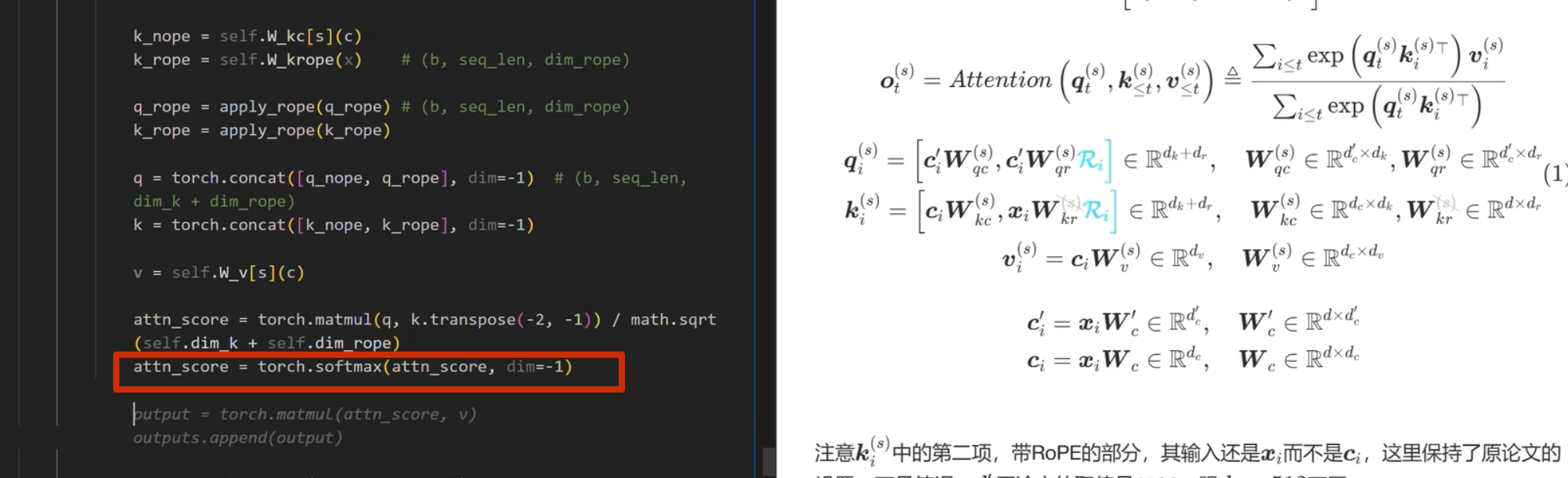
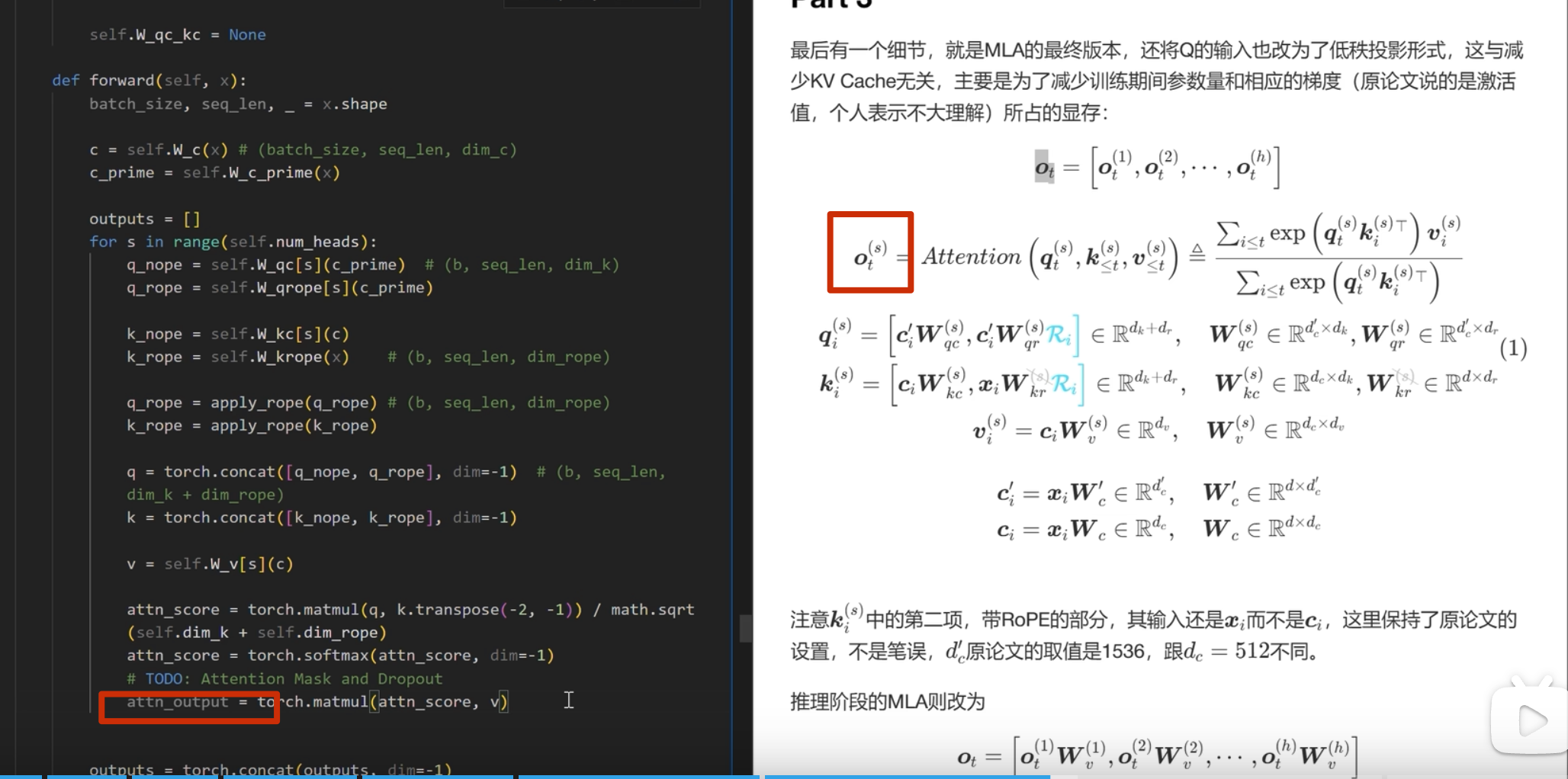
最终代码实现
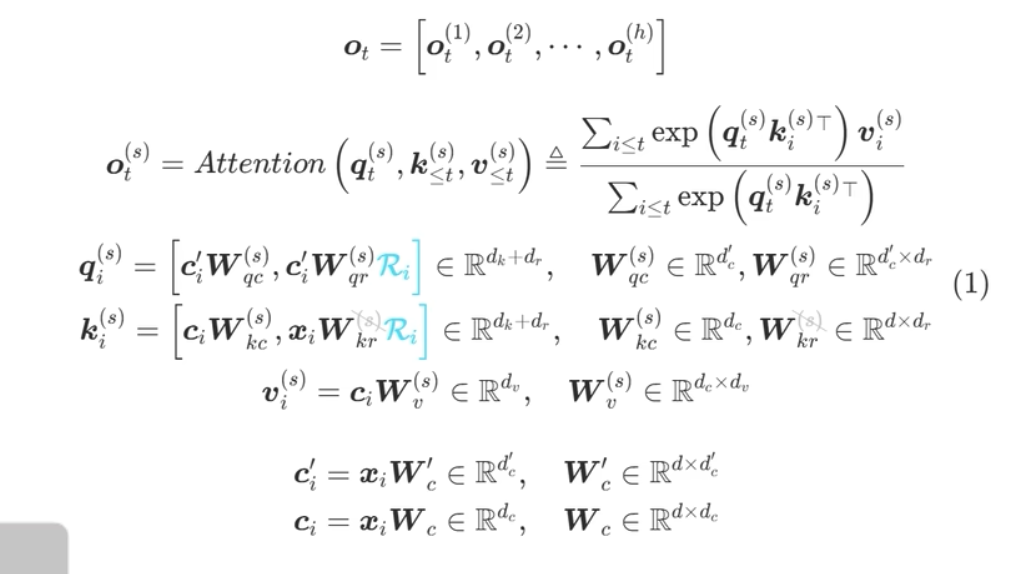
首先实现下面的
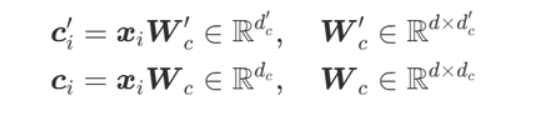
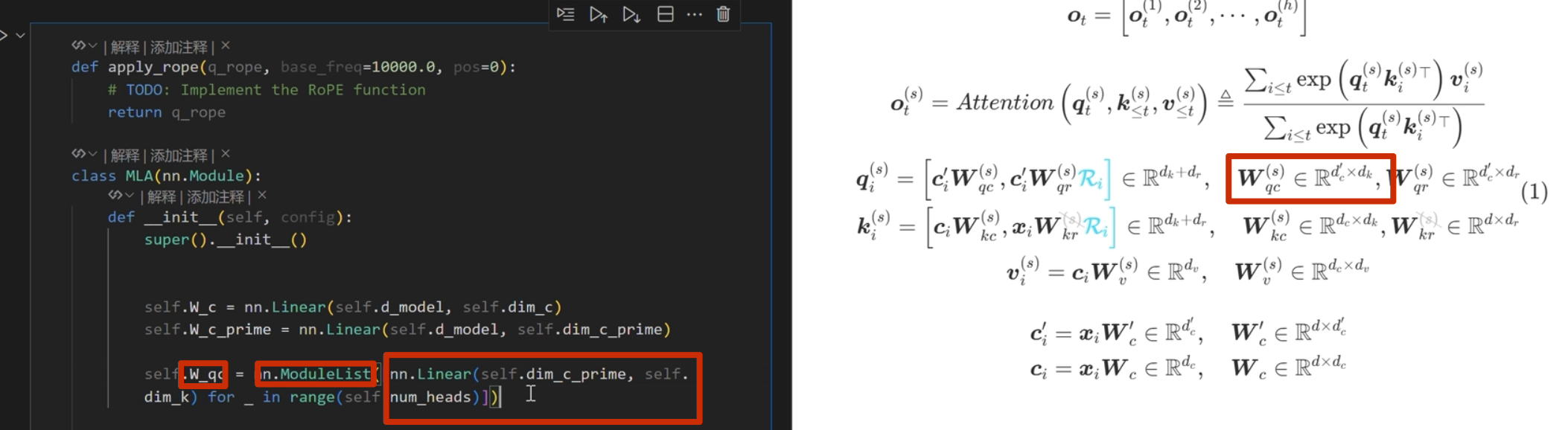
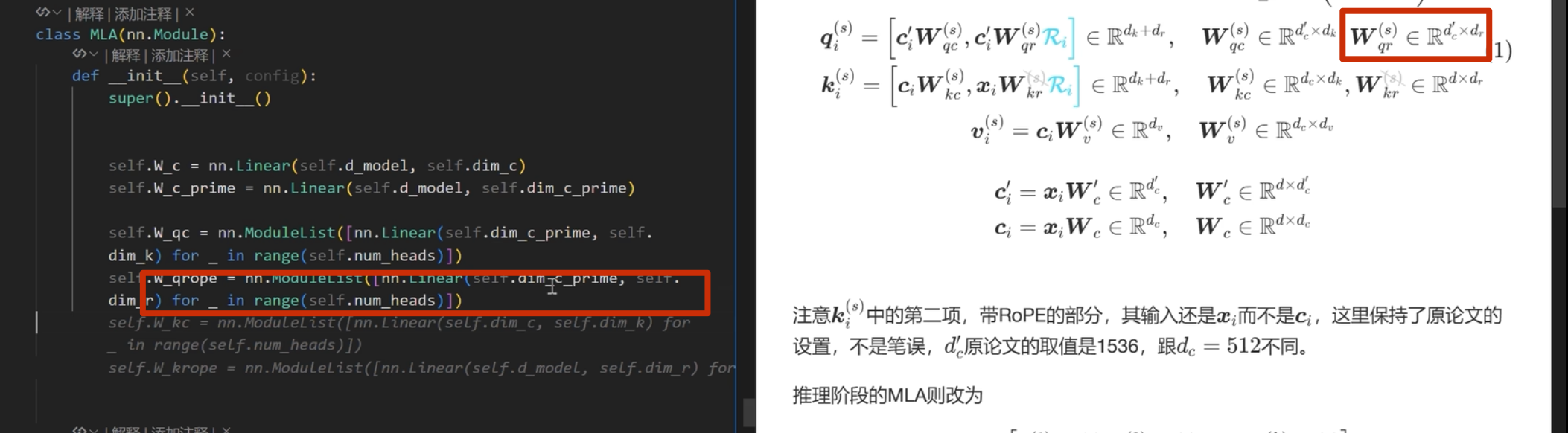
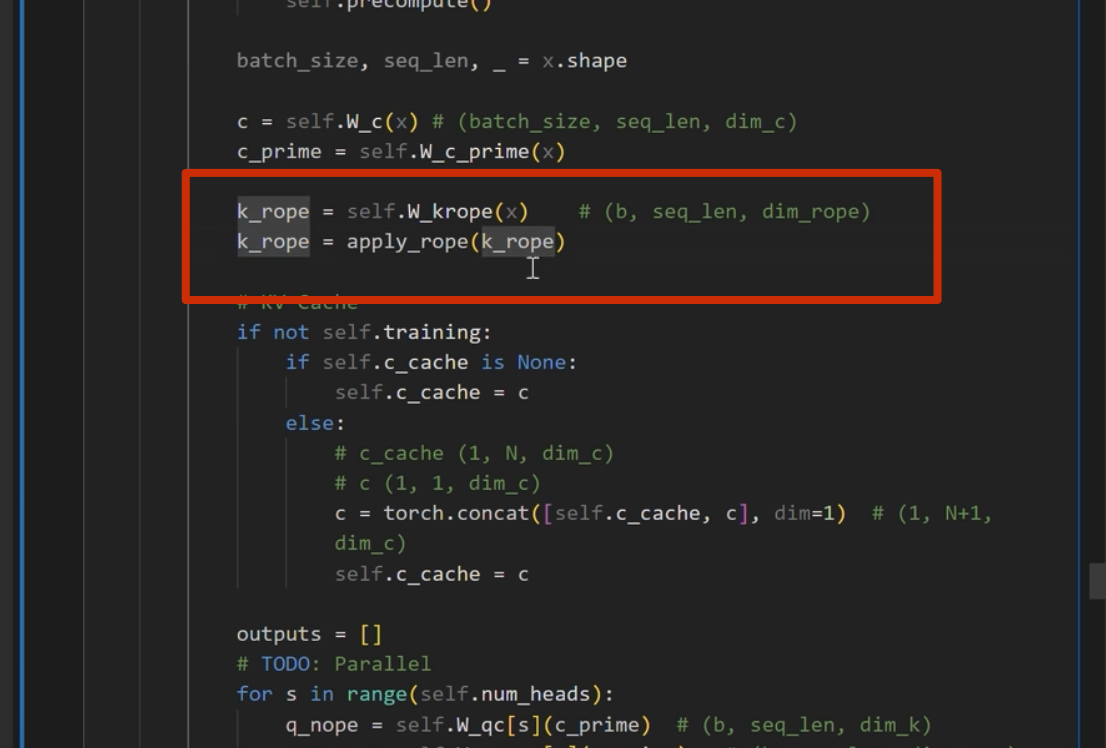
注意这里 k 是直接从 c_i和 xi 进行投影,而 不是像 q 一样从 c_i_prime投影(论文也是这么写的)
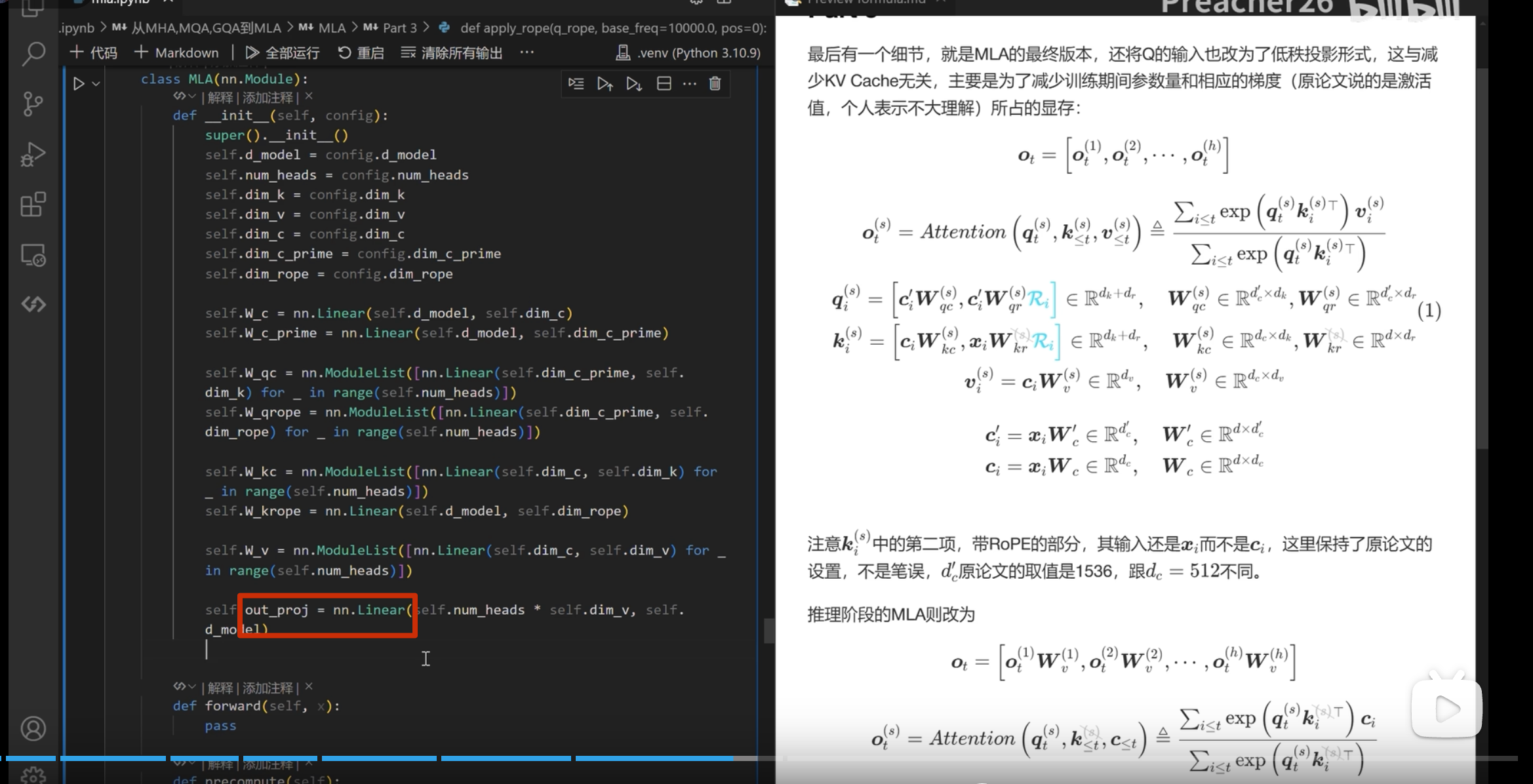
推理部分

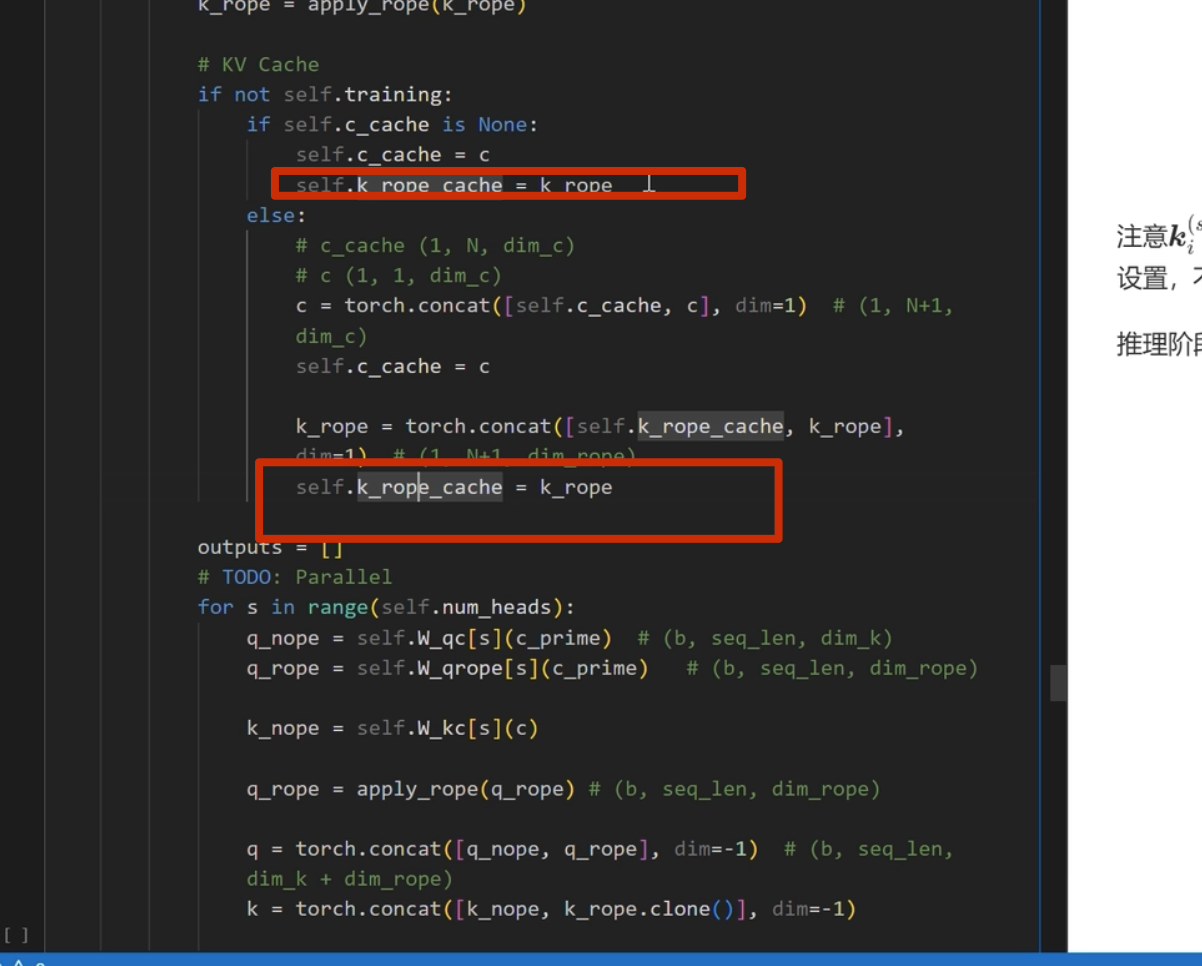
kv-cache
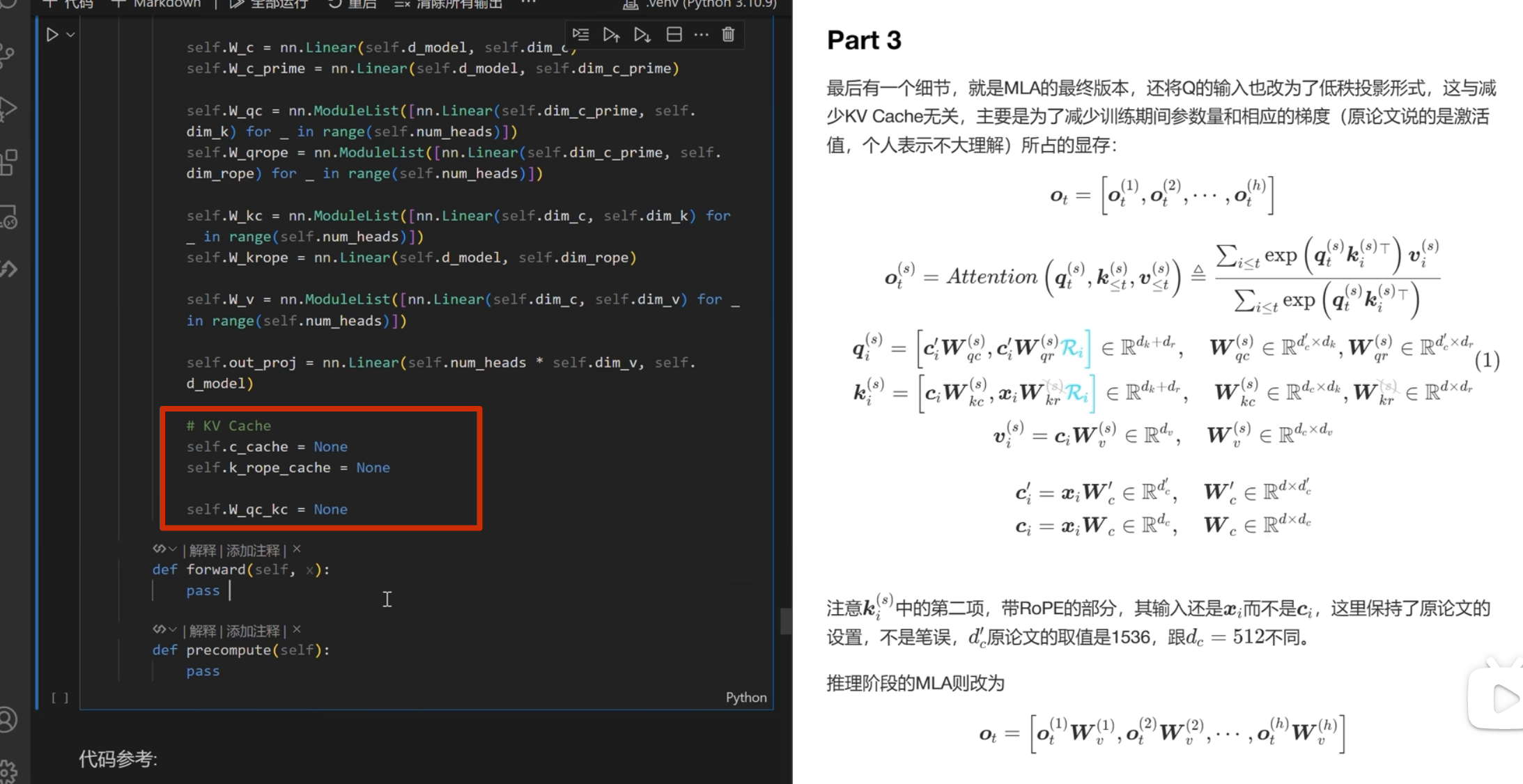
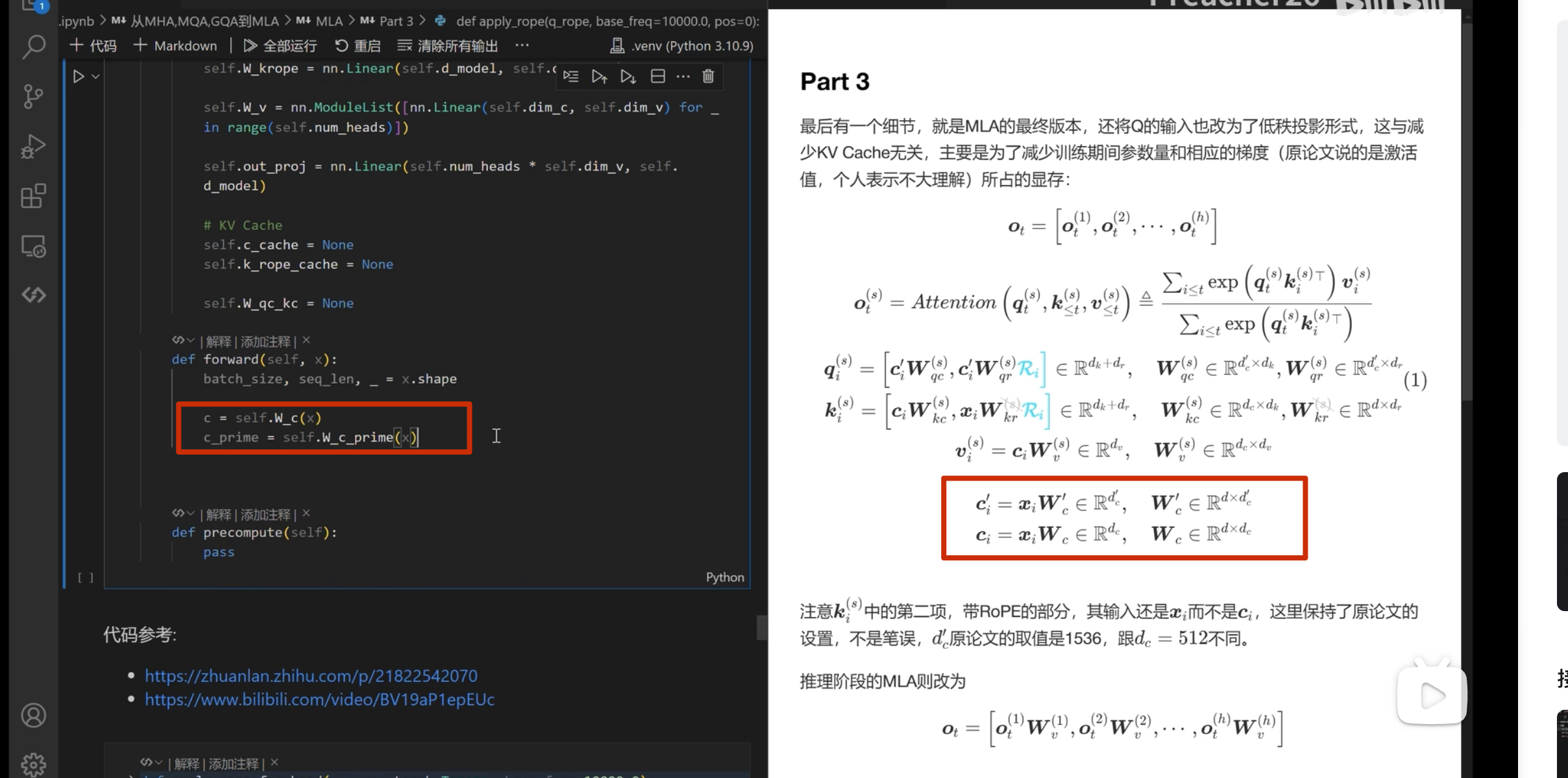

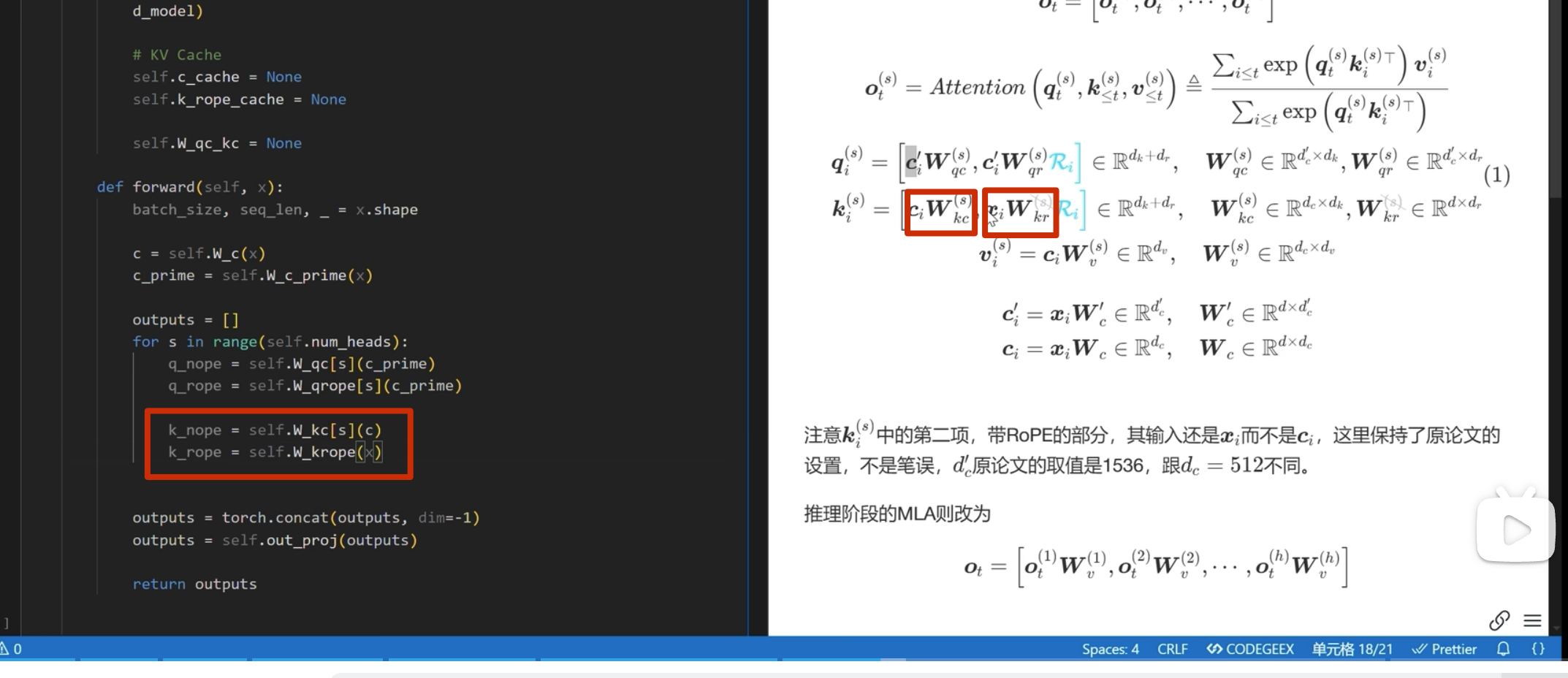
apply_rope是加入位置编码
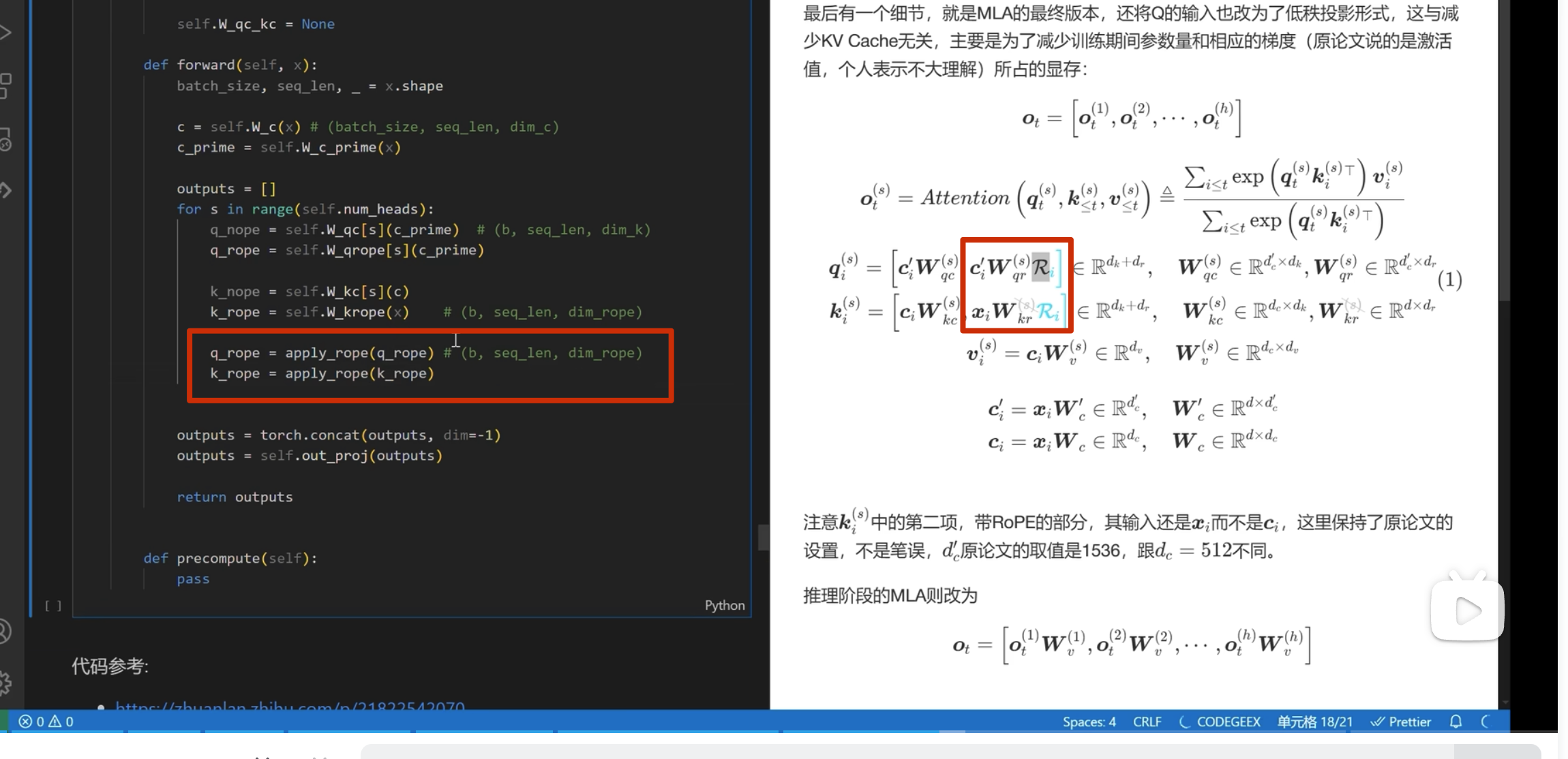
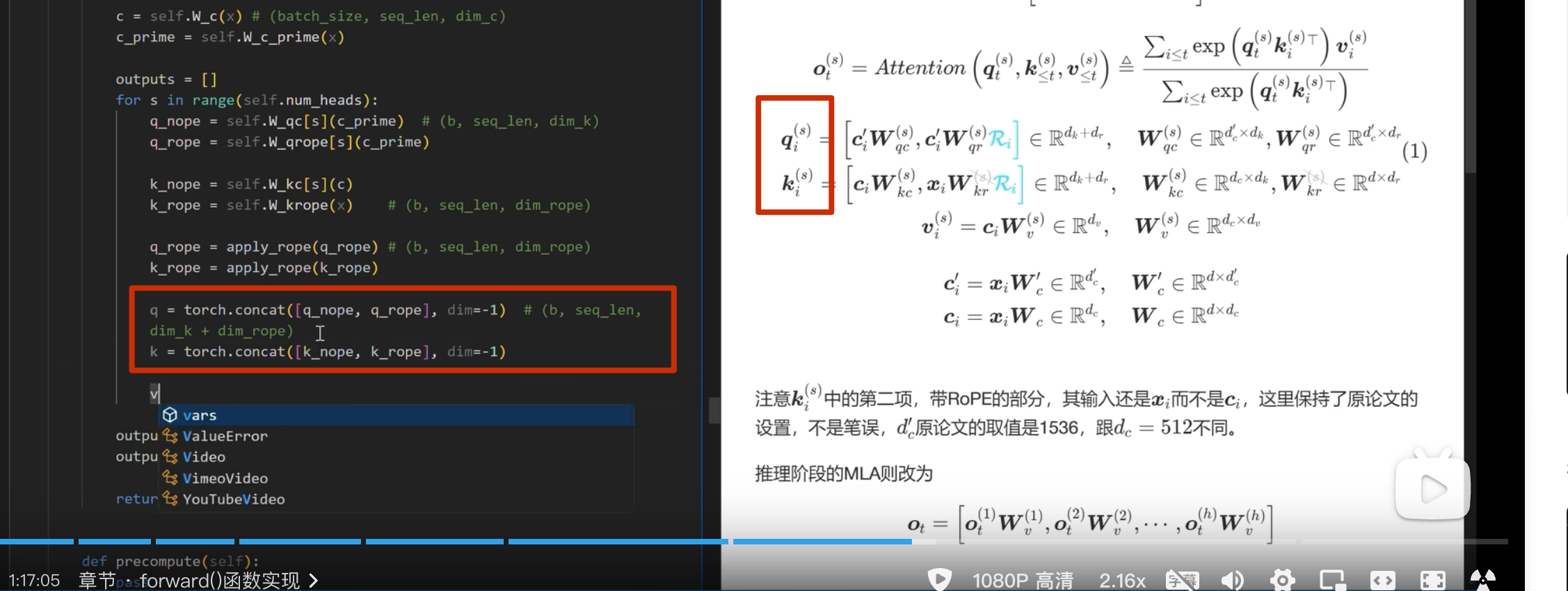

kv-cache 的计算
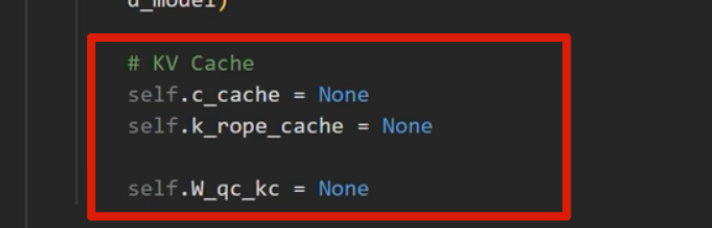
在每一次推理前调用

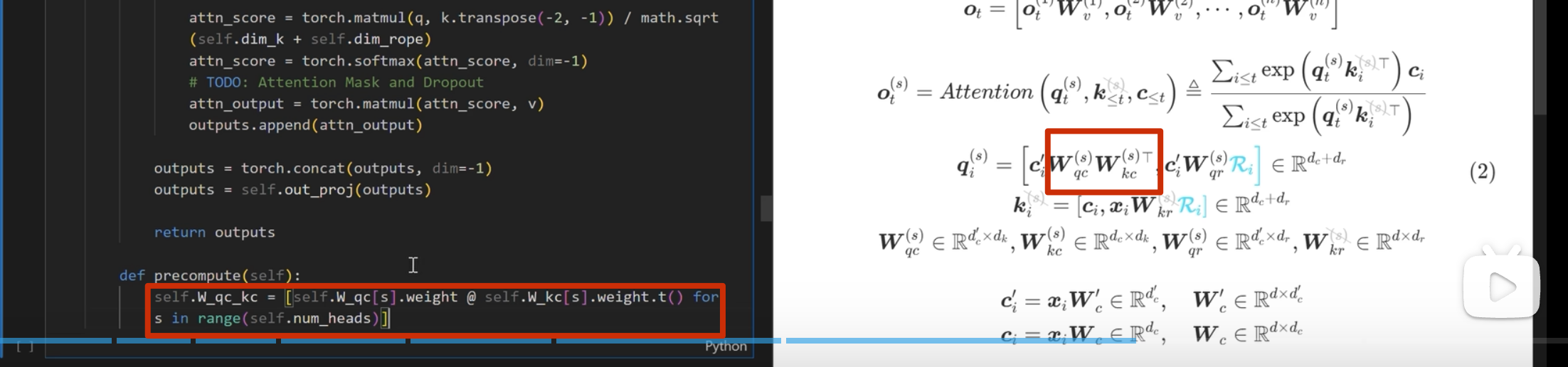
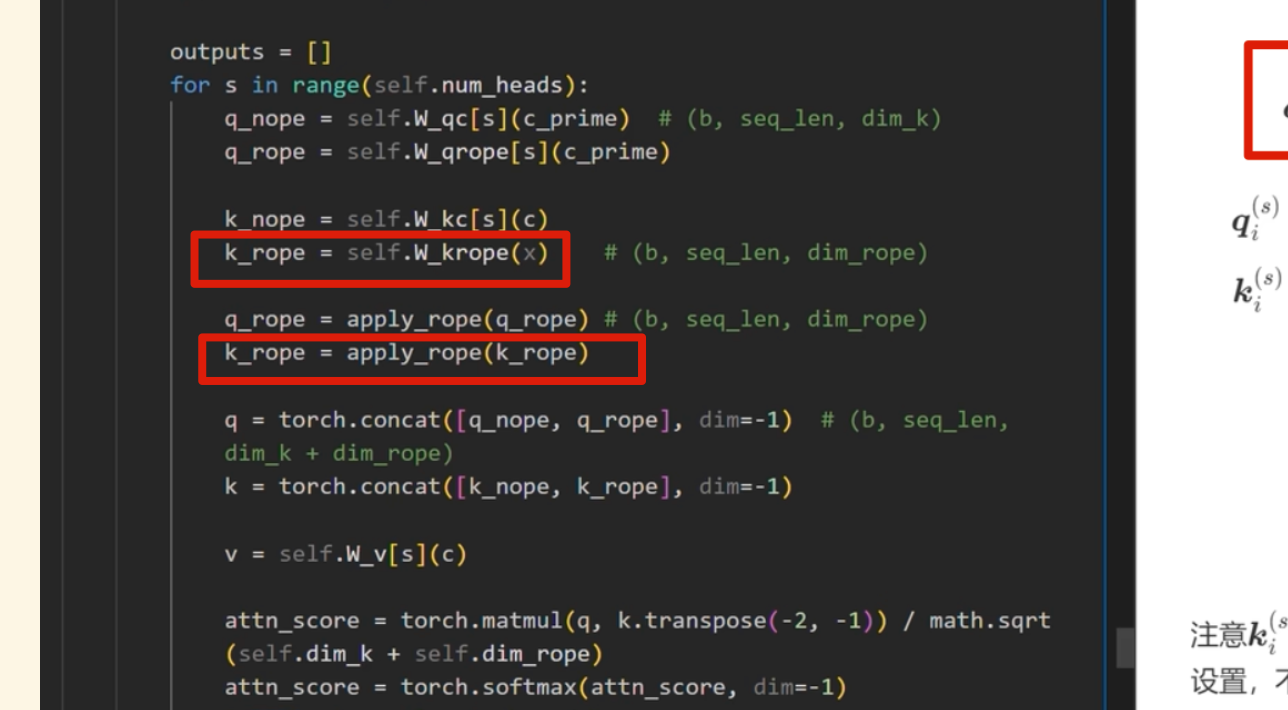
之前 k_rope是在 for 循环里面的,可以移到外面
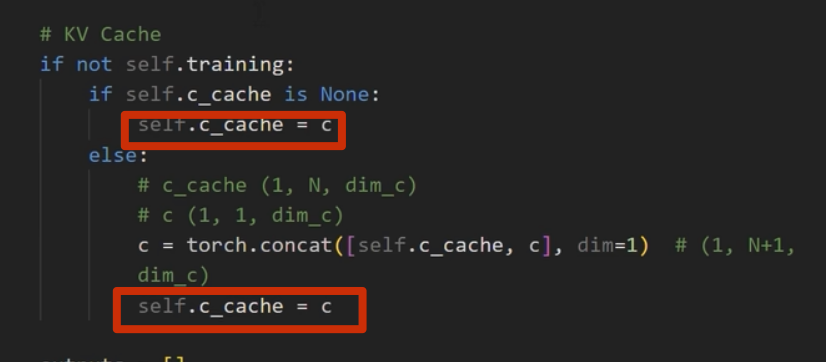
KV Cache

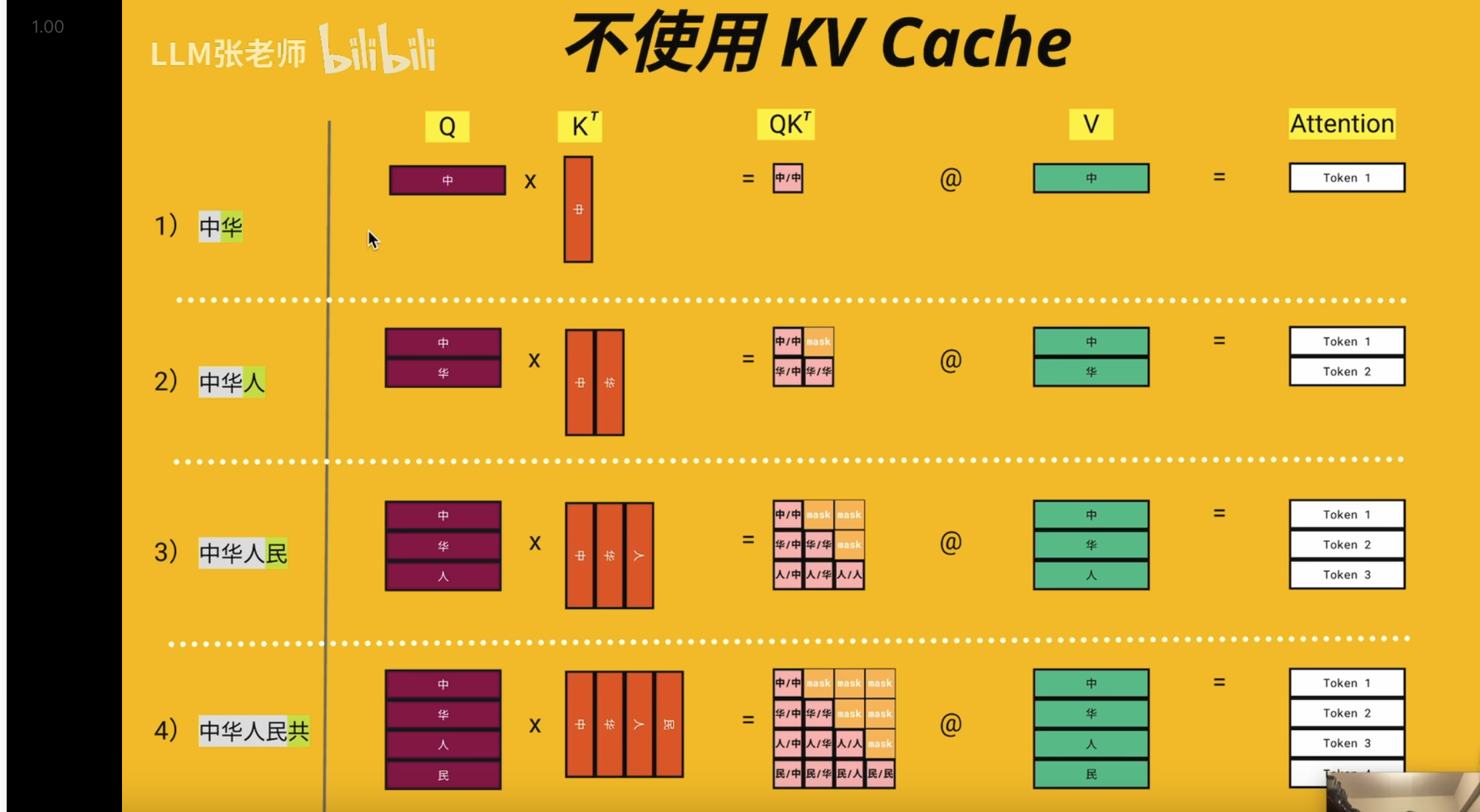
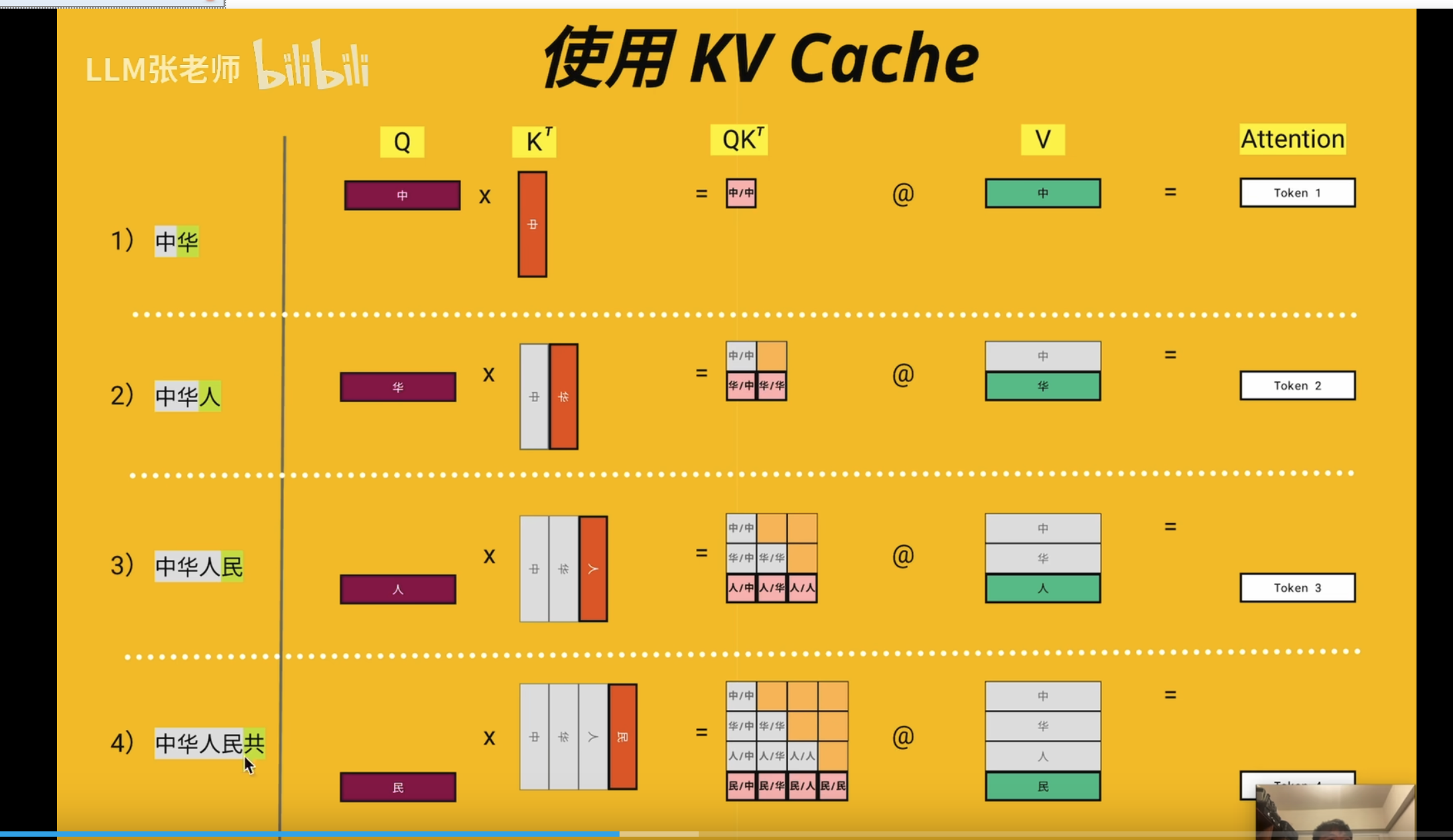
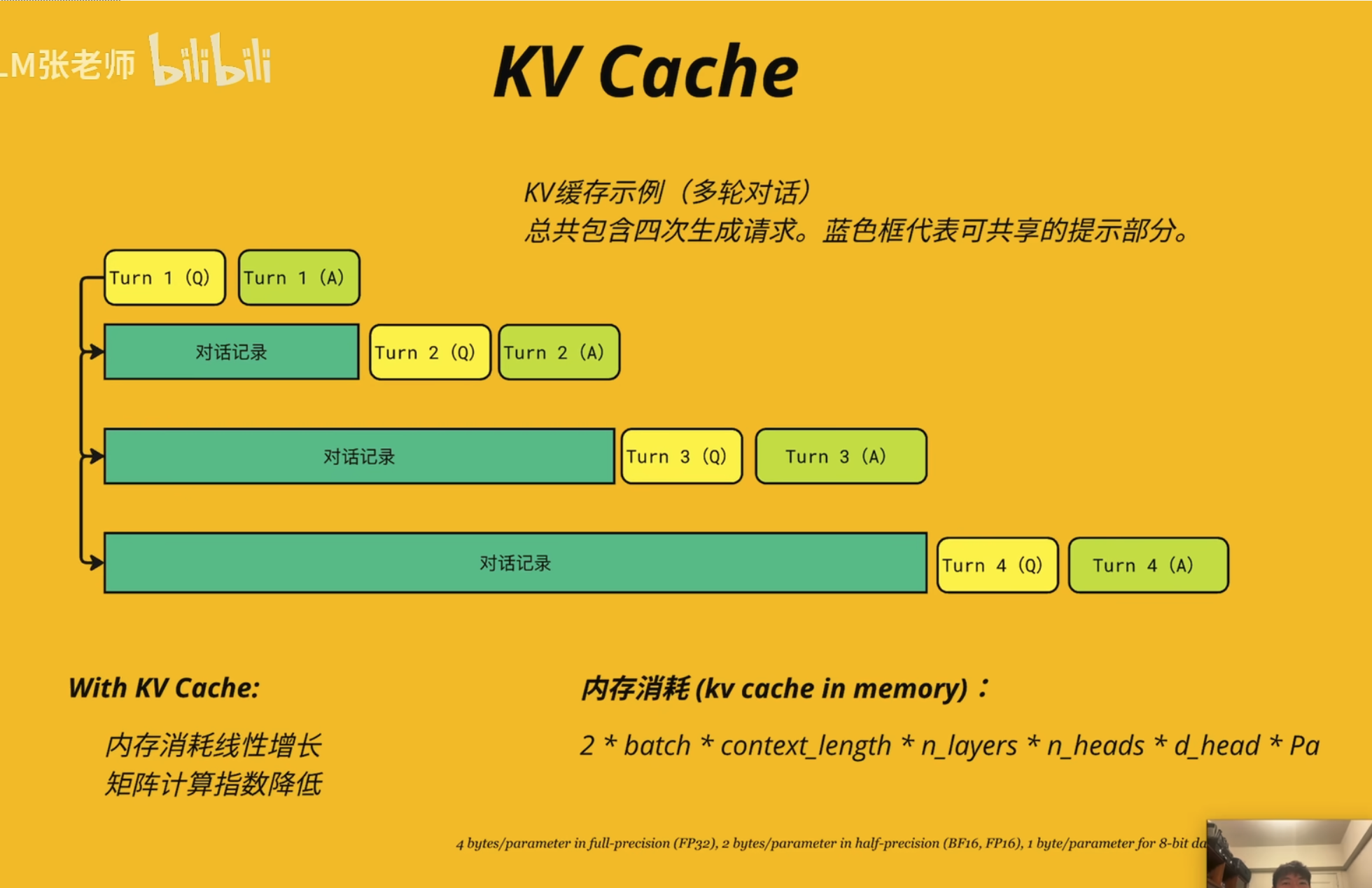


位置编码
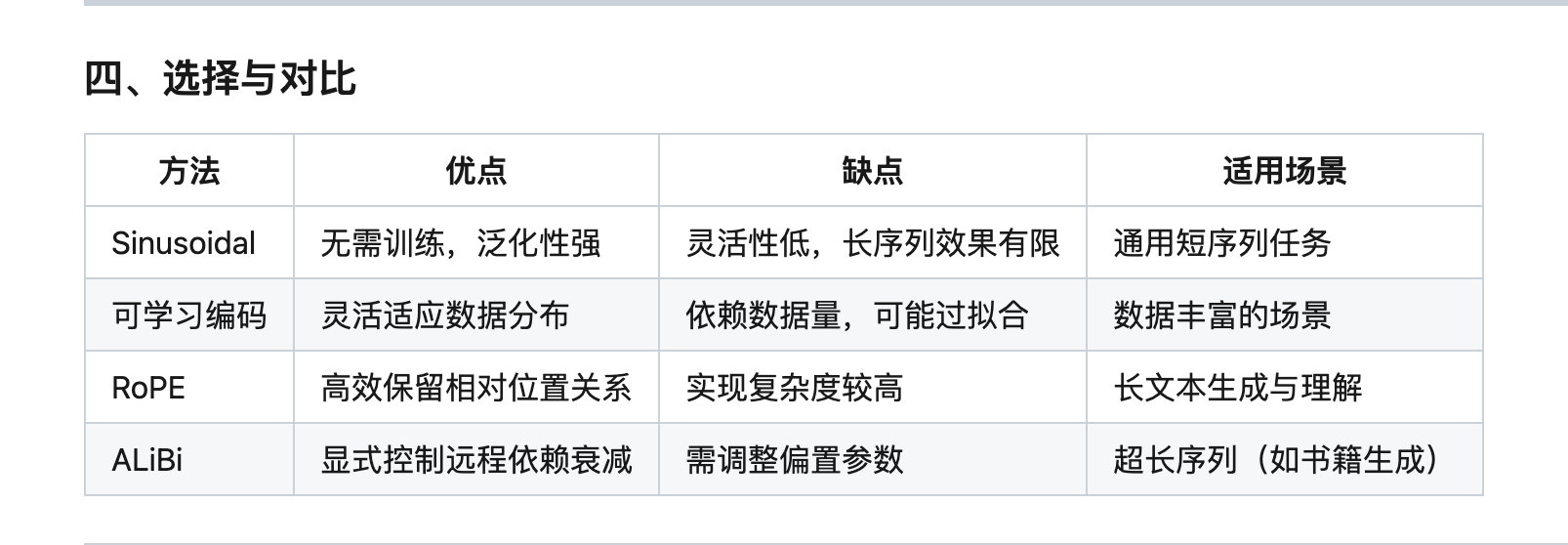


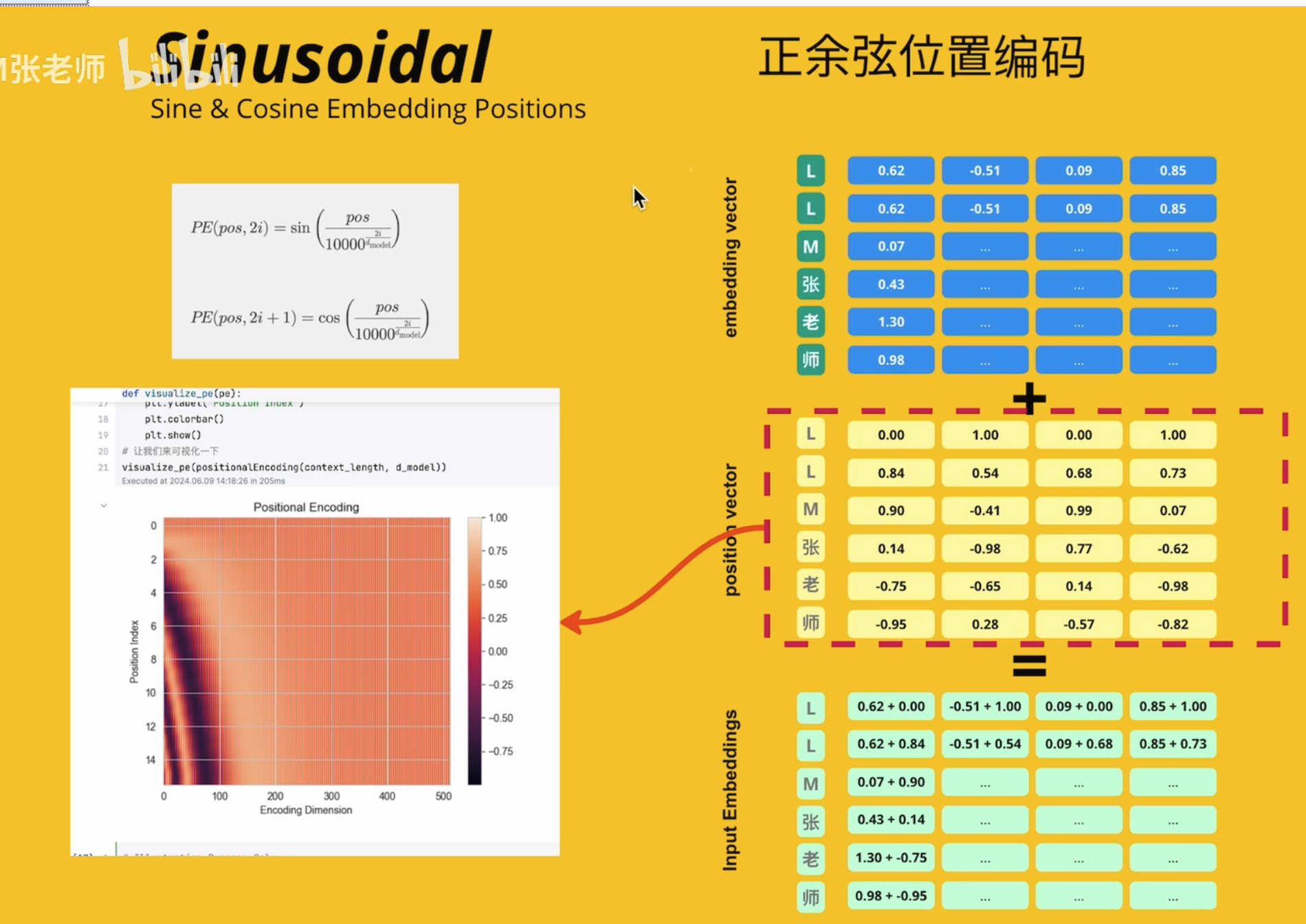

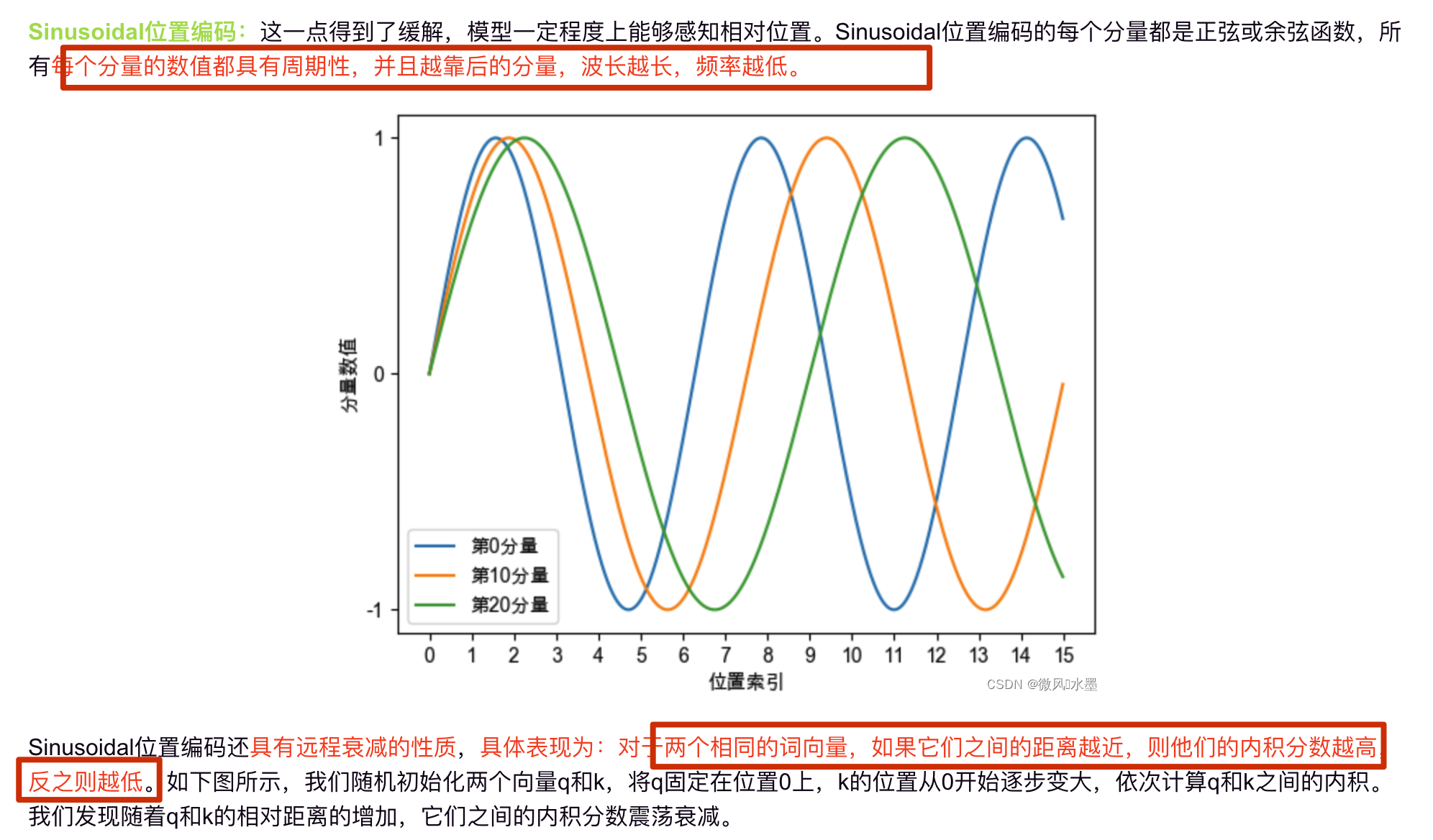
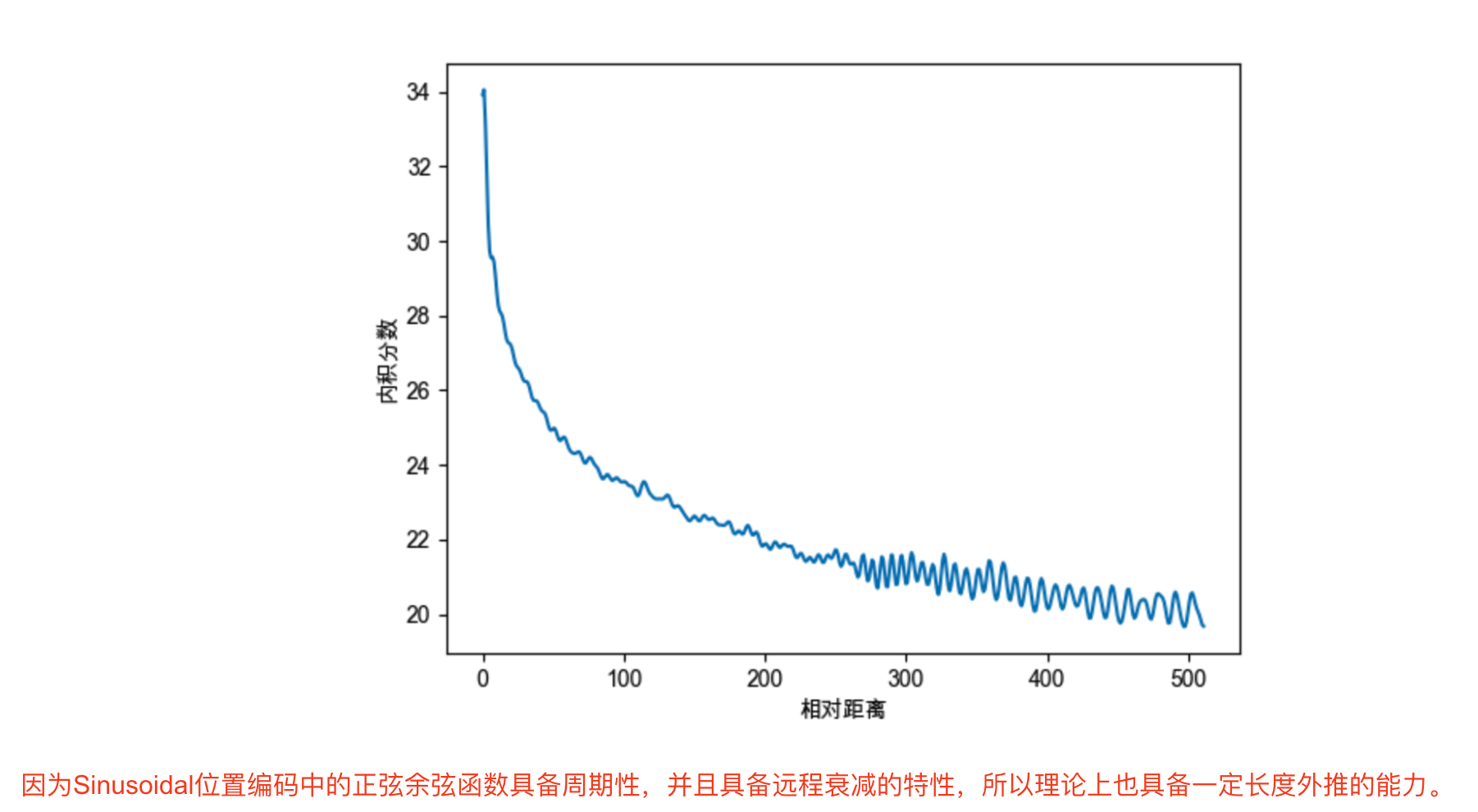

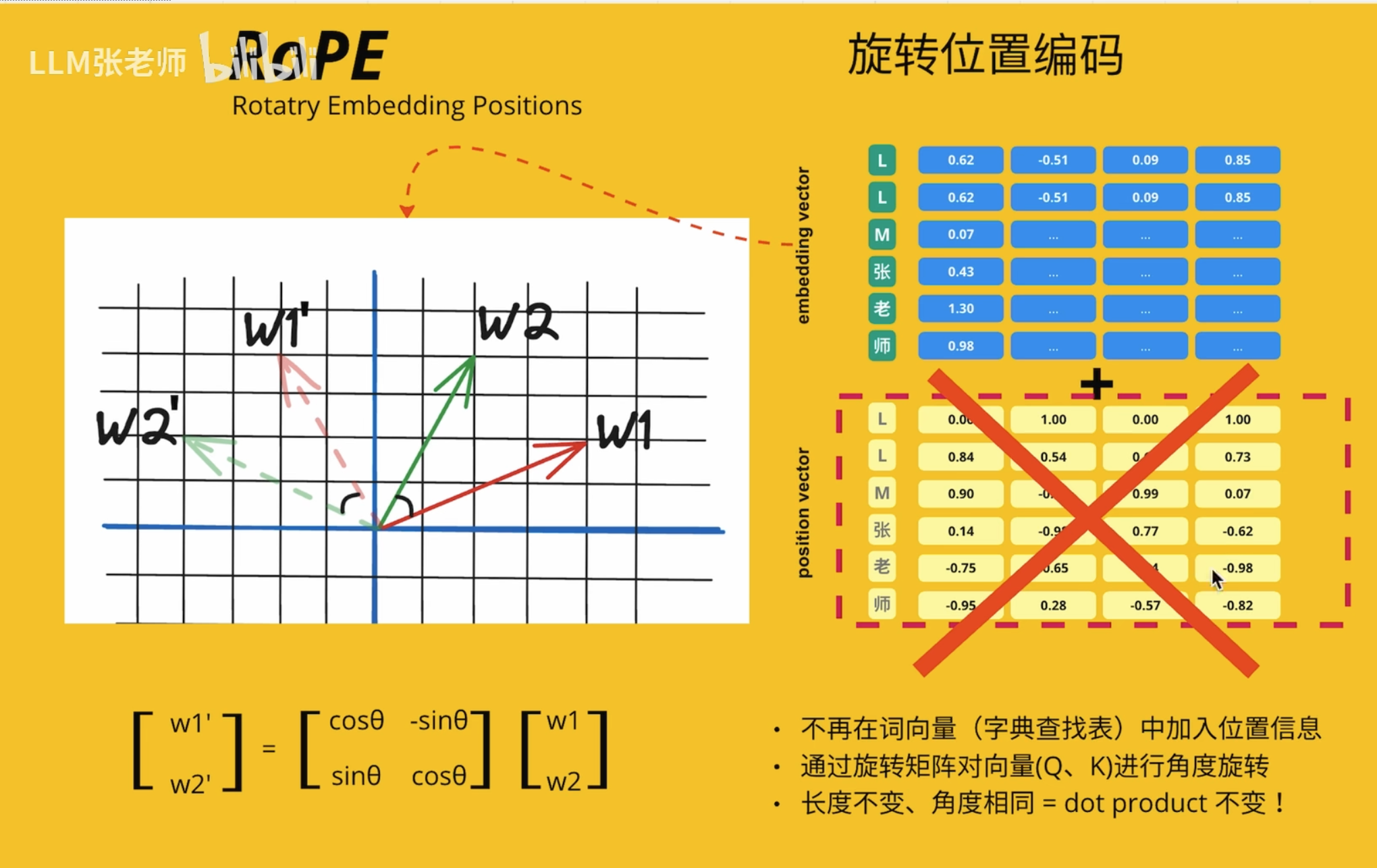
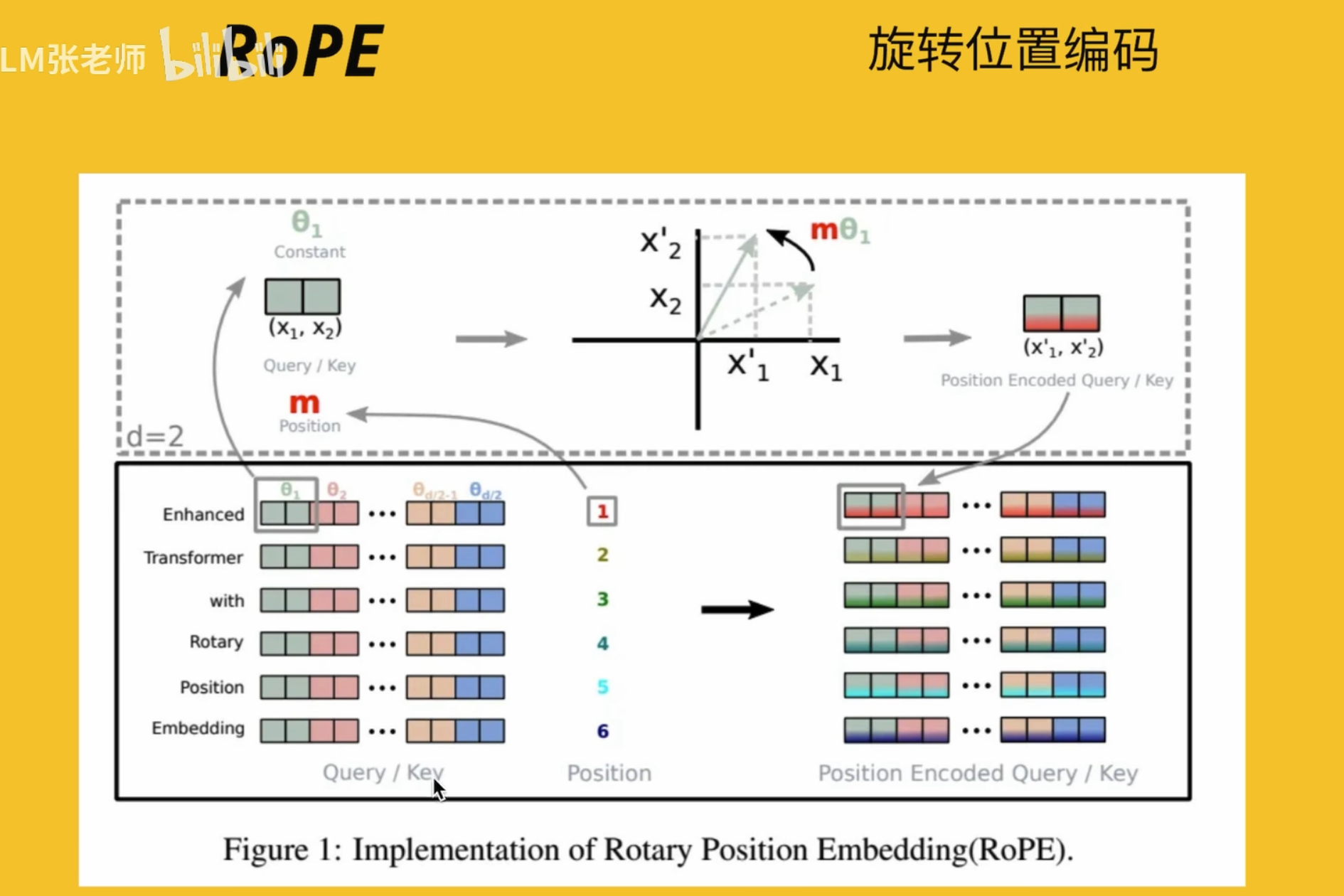
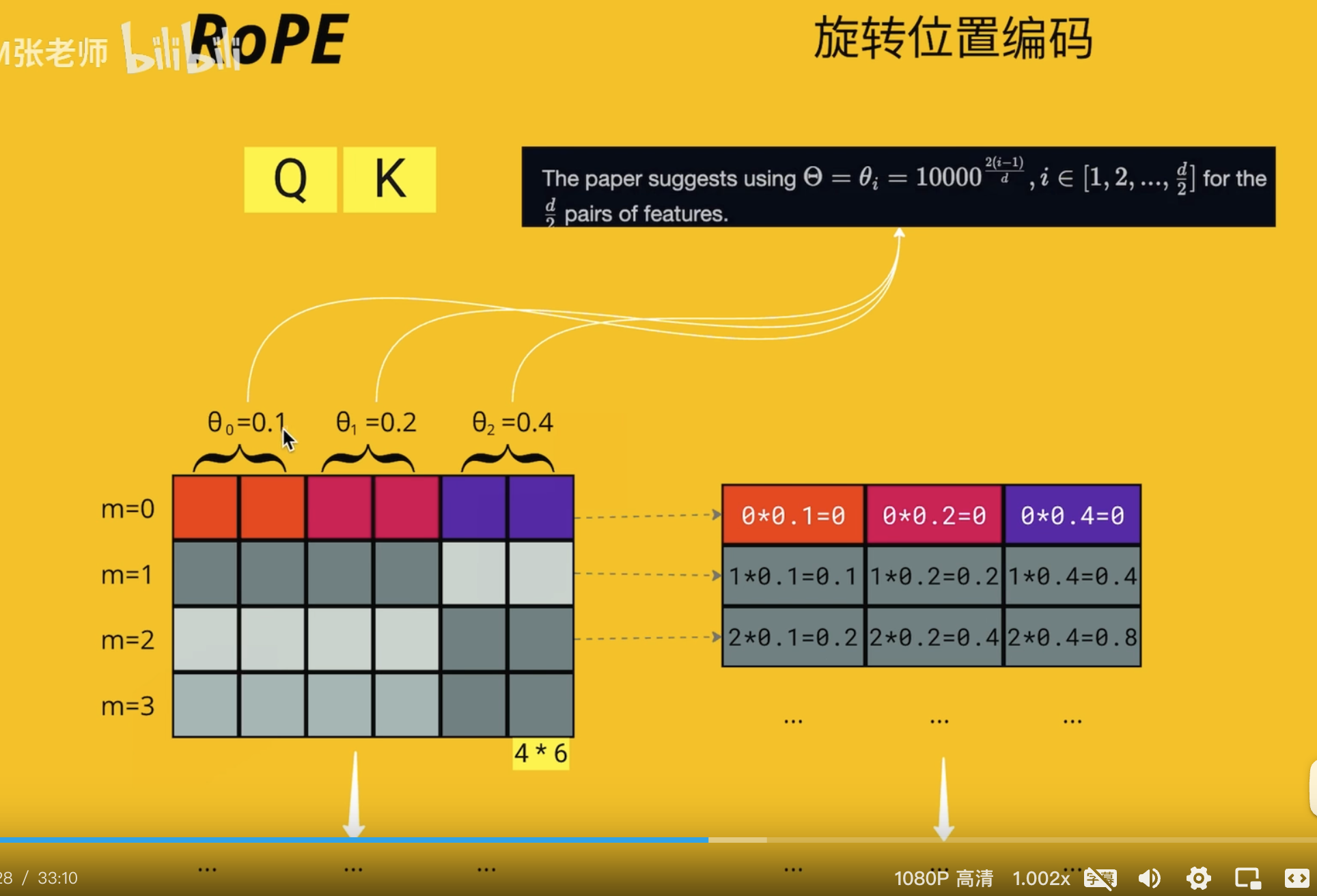
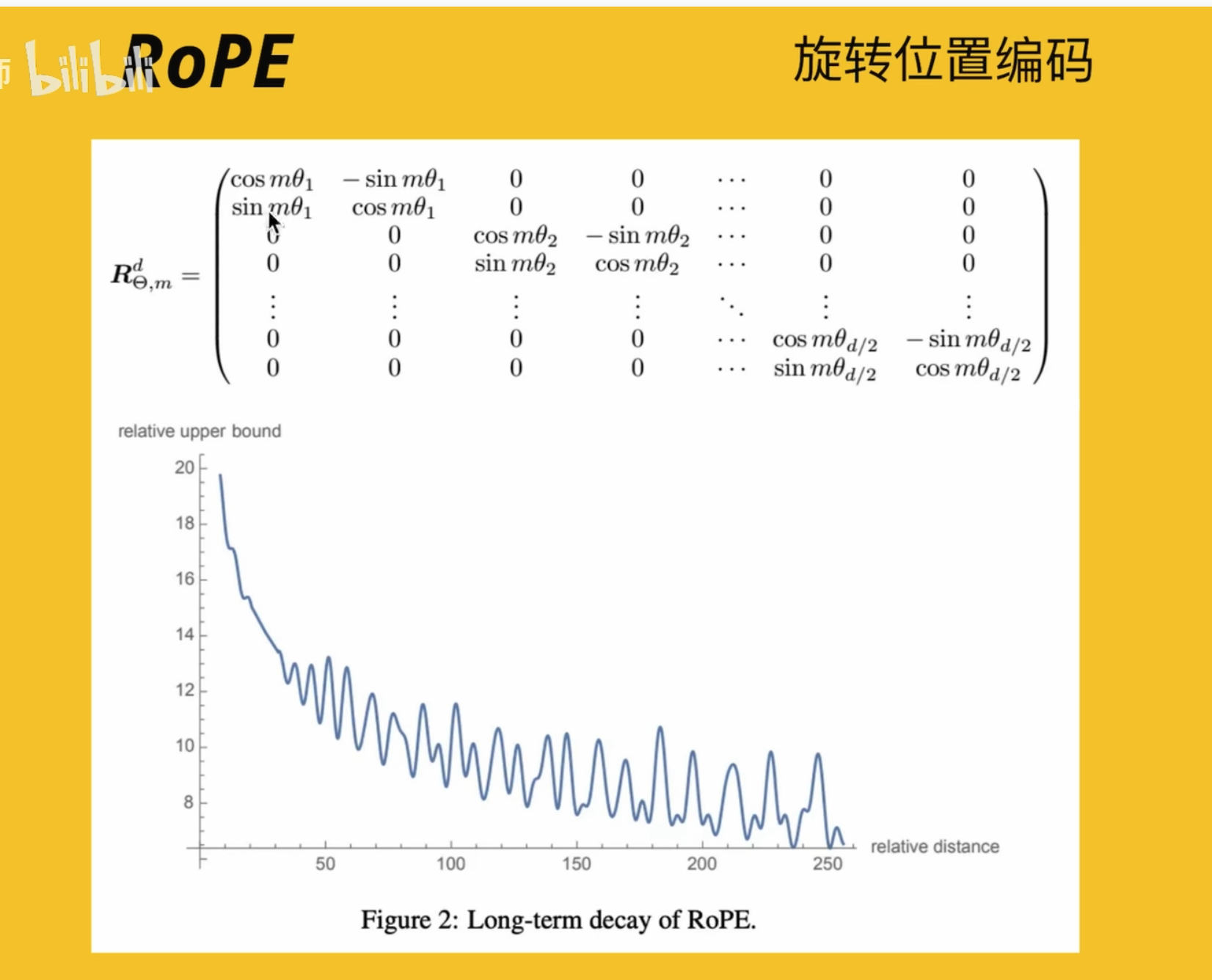
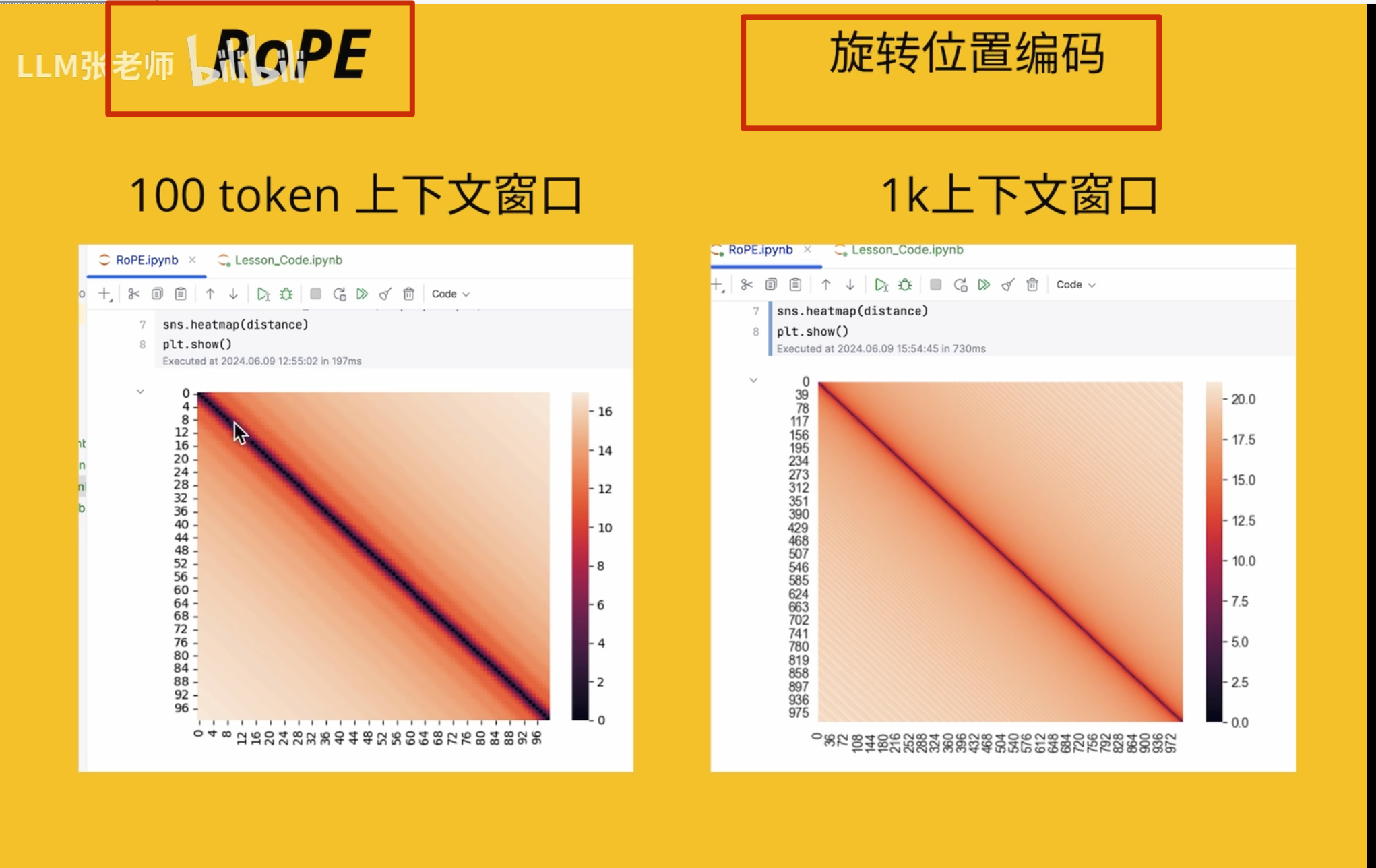

基于 Rope 发展来的,但是很复杂
(针对一些中间变量变化特别大的情况做优化)

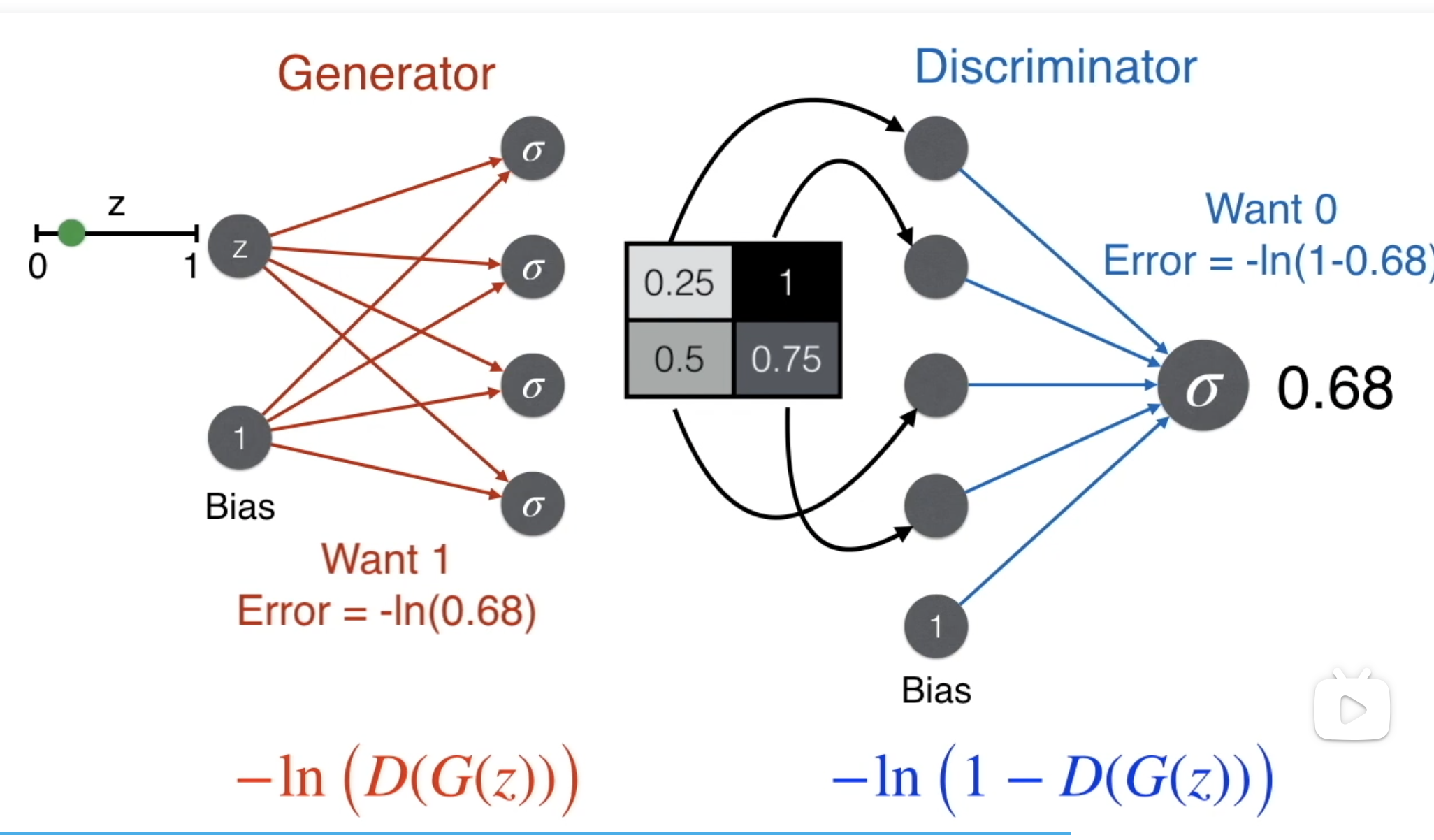
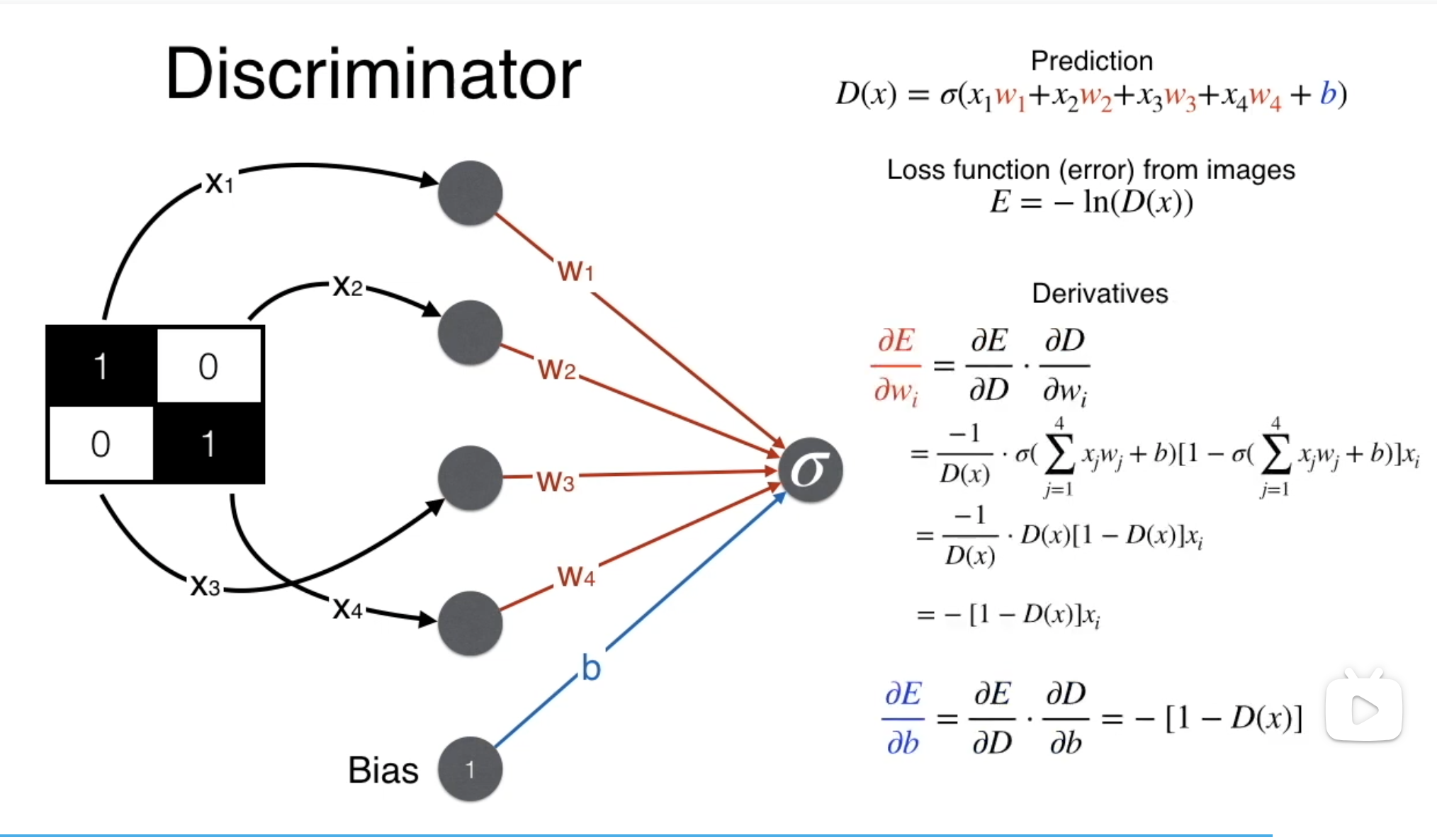
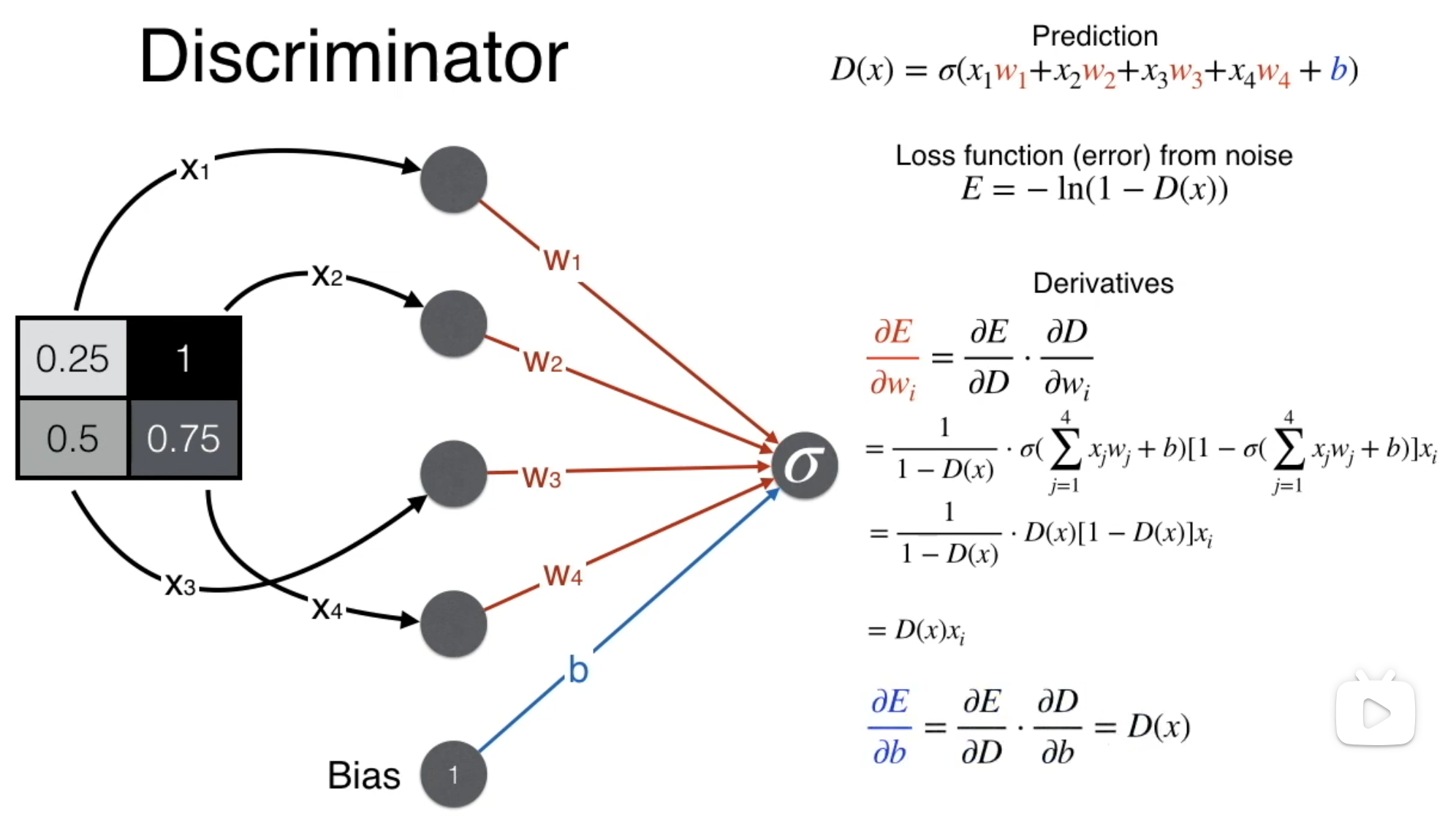
GAN
自监督学习
参考https://www.cnblogs.com/polly333/p/17791786.html
1、背景
为什么自监督火了?
- 大模型火了,数据需求量大
- 数据需求量大,导致标注成本提升
- 人工标准有一定误差
另一个层面来讲:
Yann Lecun在AAAI 2020的演讲中,指出目前深度学习遇到的挑战:
- 监督学习:深度模型有海量参数,需要大量的label数据,标注成本高、扩展性差,难以应用到无标记或标记数据少的场景。
- 强化学习:agent需要和环境大量的交互尝试,很多实际场景(例如互联网搜索推荐、无人驾驶)中交互成本大、代价高,很难应用。
而人类和动物学习快速的原因:最重要的是观察世界,而不是靠大量的监督、强化学习。自监督学习的思想就是 通过构造任务来提升预训练模型预测能力 ,即Predicting everything from everything else。具体方法是假装输入中的一部分不存在,然后基于其余的部分用模型预测这个部分,从而学习得到一个能很好地建模输入语义信息的表示学习模型
基于以上的问题,我们可以通过自监督的方法一定程度上进行解决。当然,自监督的方法也不是完全正确的,但是可以提高标注和训练的速度,减少人为因素的干扰
2、自监督学习理论
Self-Supervised Learning 的目的一般是使用大量的无 label 的资料去Pre-train一个模型,这么做的原因是无 label 的资料获取比较容易,且数量一般相当庞大,我们希望先用这些廉价的资料获得一个预训练的模型,接着根据下游任务的不同在不同的有 label 数据集上进行 Fine-tune 即可
2.1 什么是自监督学习
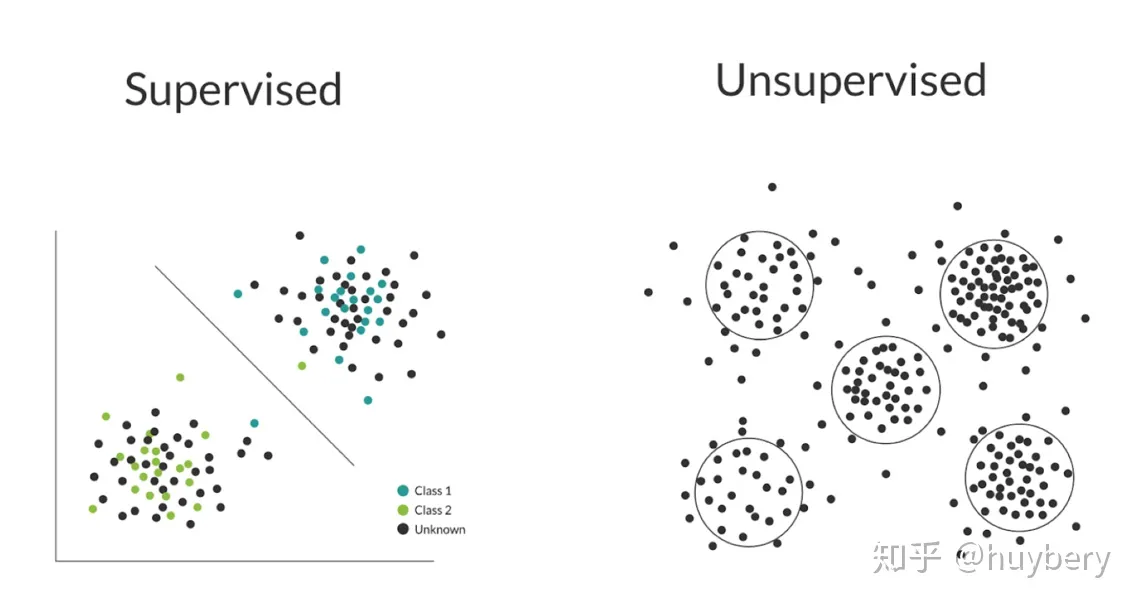
监督学习利用大量的标注数据来训练模型,无监督学习不依赖任何标签值,通过对数据内在特征的挖掘,找到样本间的关系,比如聚类相关的任务。有监督和无监督最主要的区别在于模型在训练时是否需要人工标注的标签信息。
自监督从无监督的概念中分离出来,成为一个独立的概念,通常为定义一个Pretext task (辅助任务),即从无监督的数据中,通过巧妙地设计自动构造出有监督(伪标签)数据,学习一个预训练模型。
具体来说自监督可以定义为:
从部分无标签数据自身出发通过设计半自动预训练任务进行处理学习具有监督性质的表征信息。
通过这部分学习到特征的数据去预测其他无标签的数据,实现标签的泛化
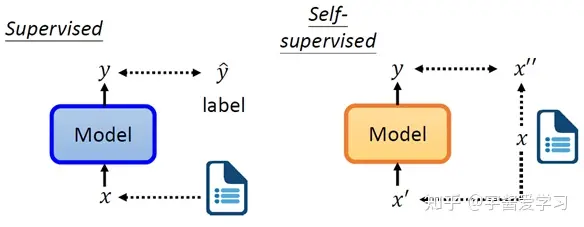
下面是 BERT这种预训练模型为例子(BERT,基于transformer的双向编码表示,它是一个预训练模型,模型训练时的两个任务是预测句子中被掩盖的词以及判断输入的两个句子是不是上下句。在预训练好的BERT模型后面根据特定任务加上相应的网络,可以完成NLP的下游任务,比如文本分类、机器翻译等。https://arxiv.org/abs/1810.04805)
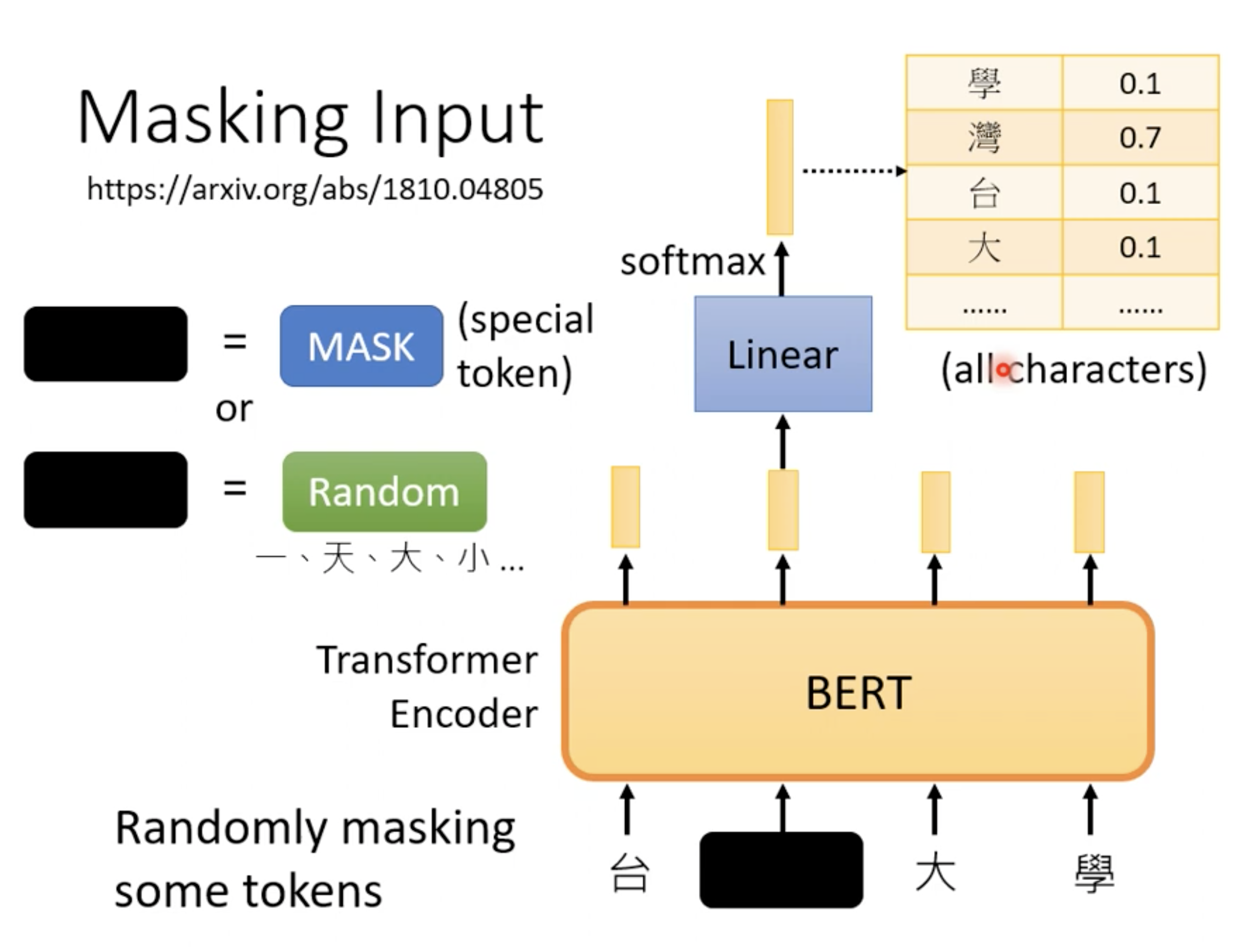
BERT预训练目标-——这里是最小化交叉熵
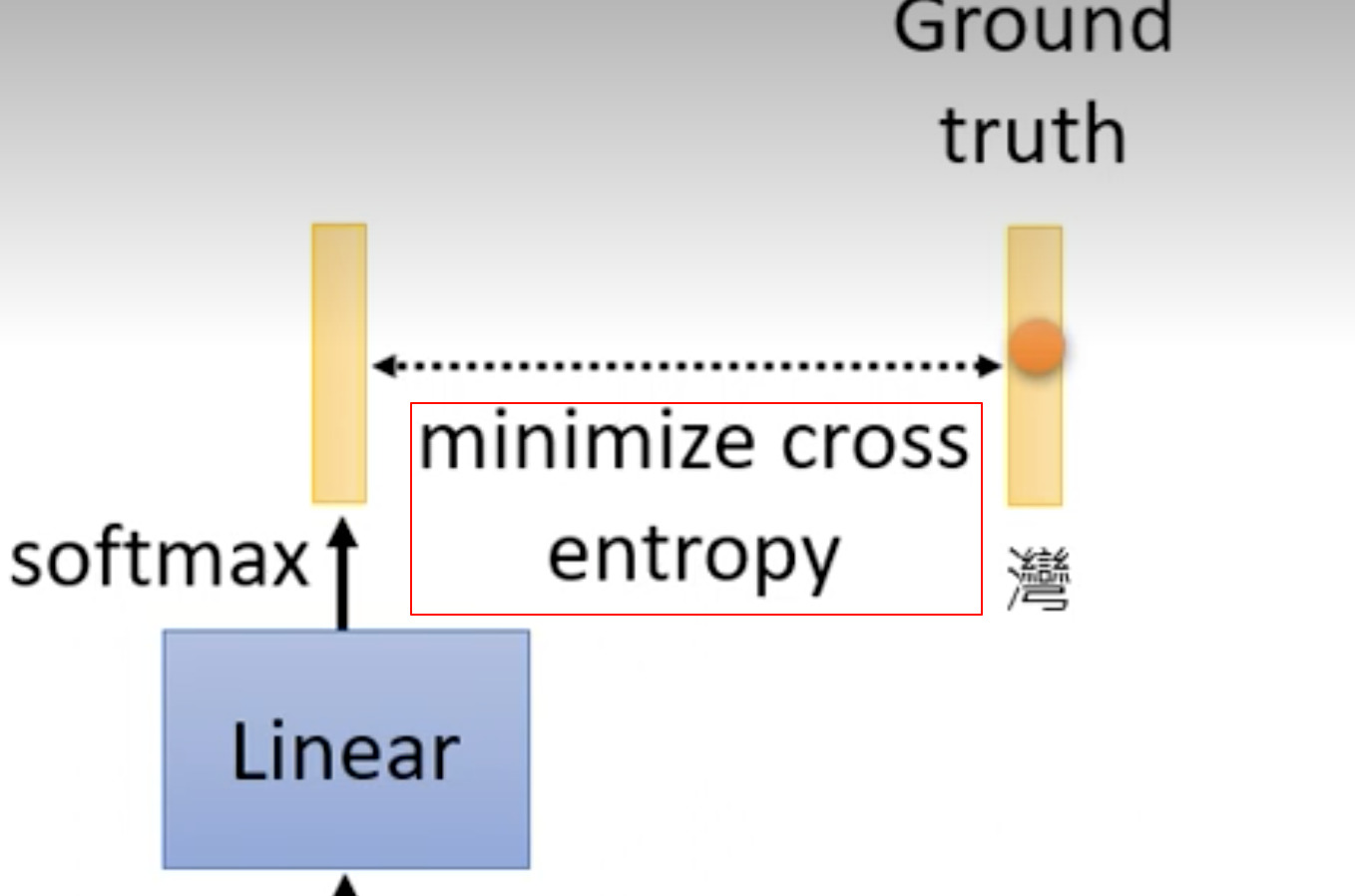
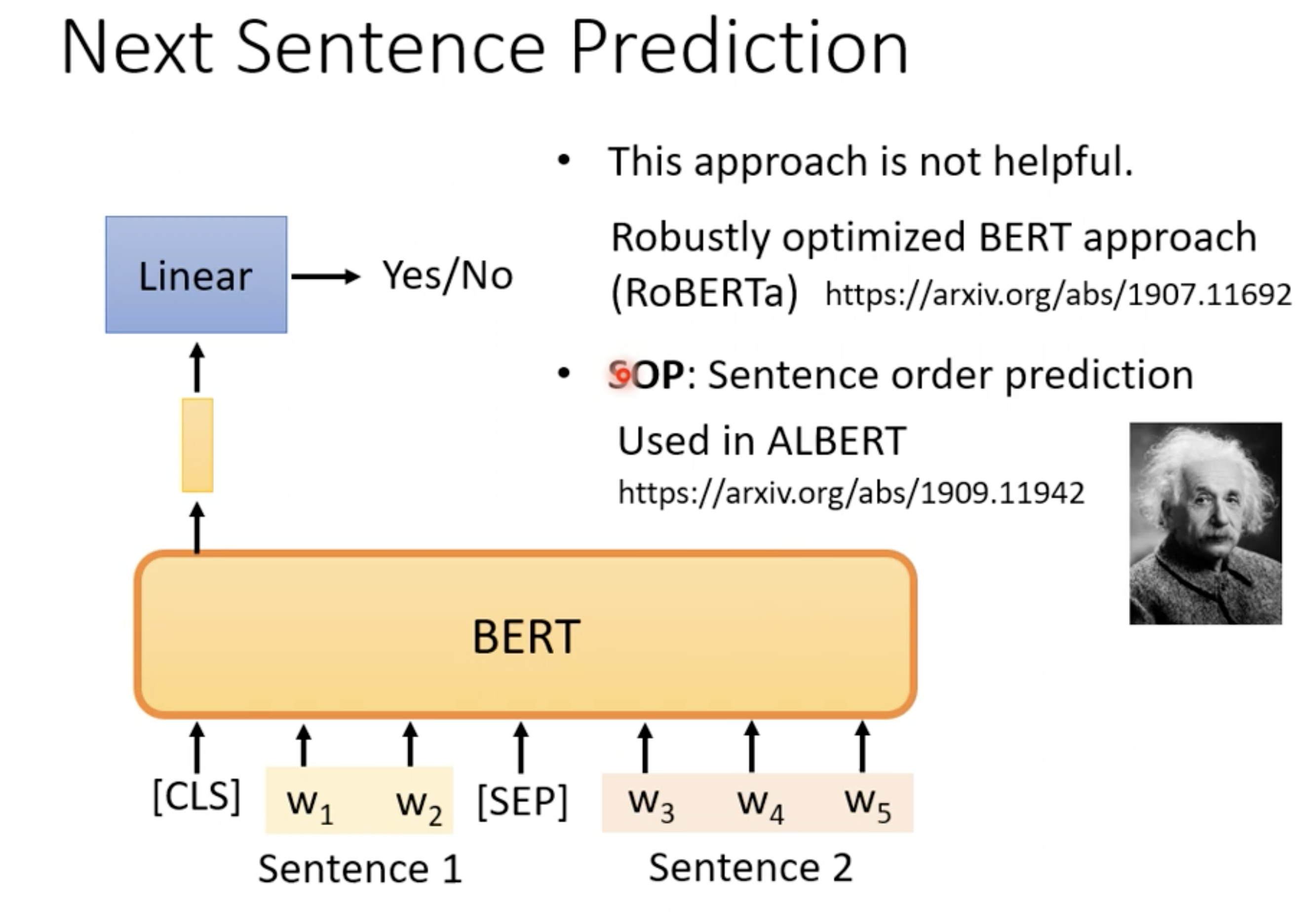
如果学习的预训练模型能准确预测缺失部分的数据,说明它的表示学习能力很强,能够学习到输入中的高级语义信息、泛化能力比较强
Self-Supervised Learning 是无监督学习里面的一种,主要是希望能够学习到一种通用的特征表达用于 下游任务 (Downstream Tasks) 。预训练阶段使用 无标签的数据集 (unlabeled data) ,想先把参数从 一张白纸 训练到 初步成型 ,再从 初步成型 训练到 完全成型 。注意这是2个阶段。这个 训练到初步成型的东西 ,我们把它叫做 Visual Representation 。预训练模型的时候,就是模型参数从 一张白纸 到 初步成型 的这个过程,还是用无标签数据集。等我把模型参数训练个八九不离十,这时候再根据你 下游任务 (Downstream Tasks) 的不同去用带标签的数据集把参数训练到 完全成型 ,那这时用的数据集量就不用太多了,因为参数经过了第1阶段就已经训练得差不多了
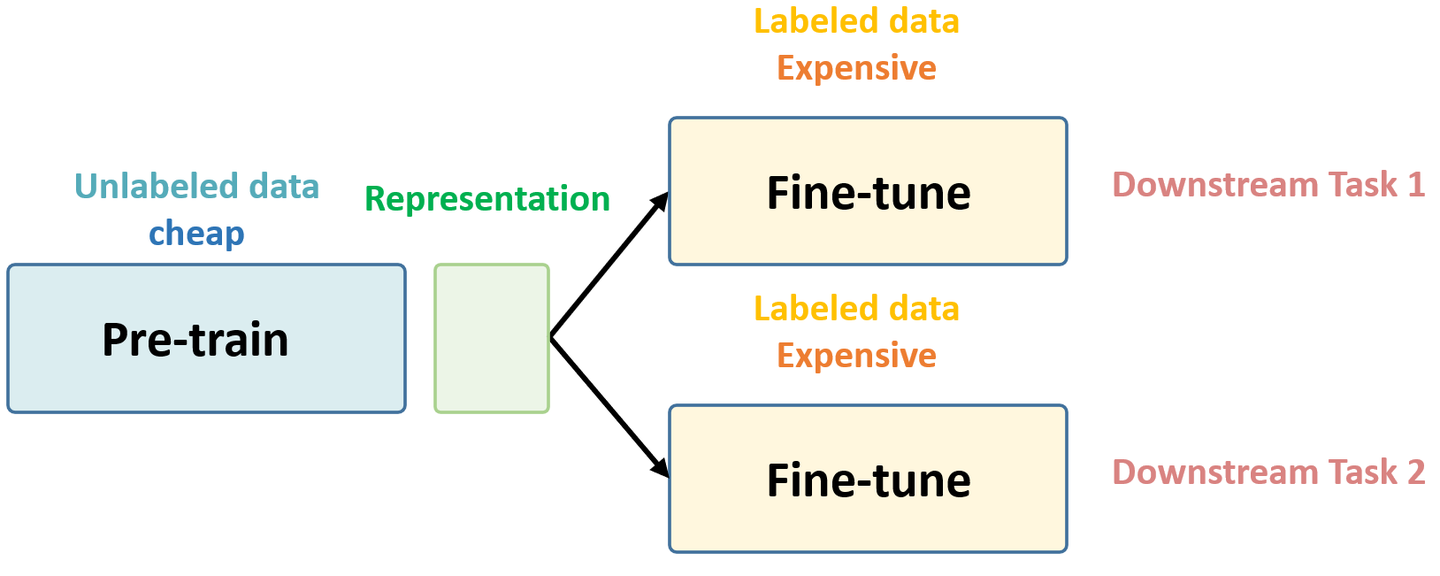
2.2 如何实现
在自监督学习中,最重要的问题是:如何定义Pretext任务、如何从Pretext任务学习预训练模型
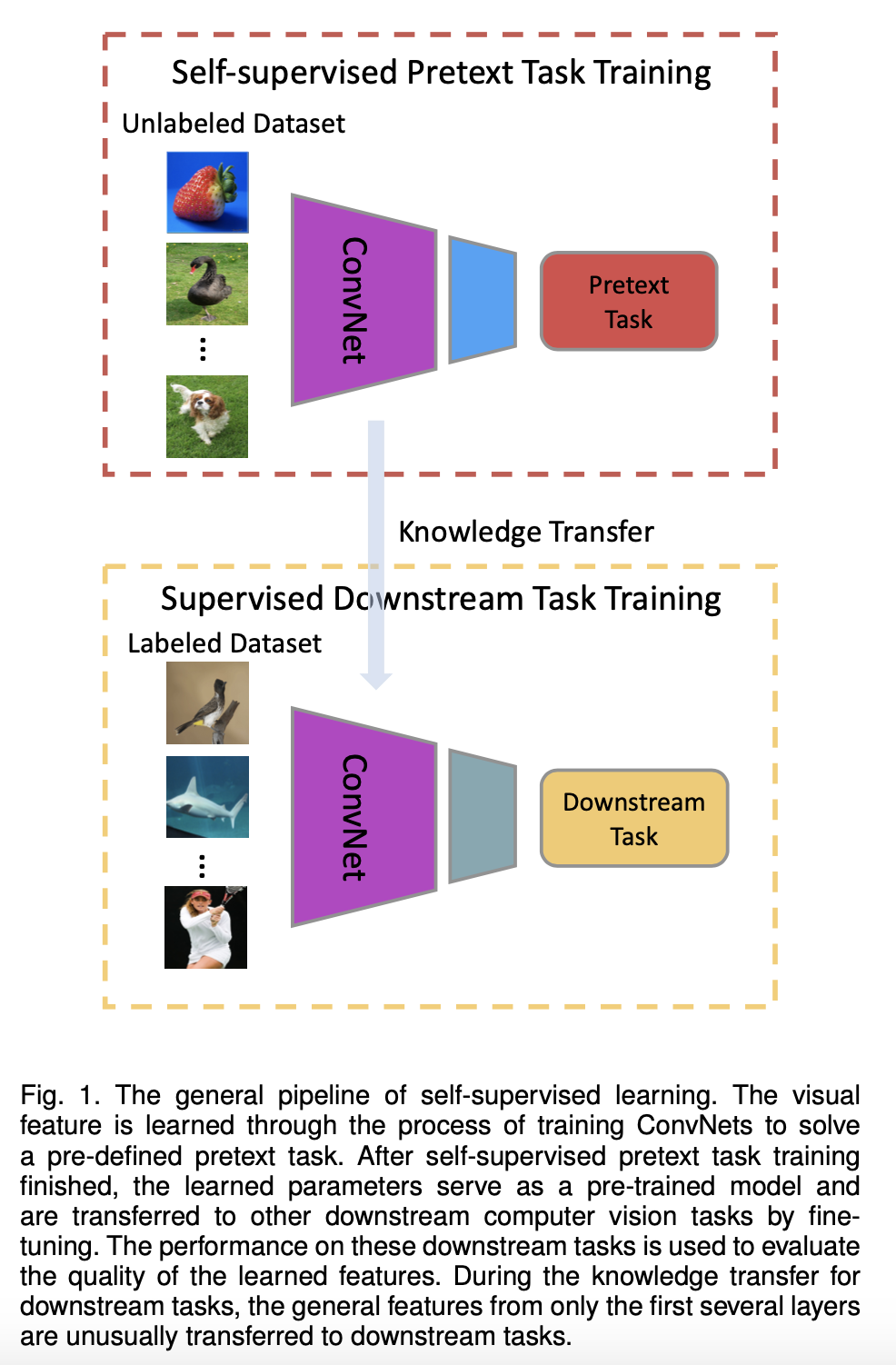
对于自监督学习来说,存在三个挑战:
- 对于大量的无标签数据,如何进行表征学习?
- 从数据的本身出发,如何设计有效的辅助任务 pretext?
- 对于自监督学习到的表征,如何来评测它的有效性?
评测自监督学习的能力,主要是 通过 Pretrain-Fintune 的模式 。
监督学习中的 Pretrain - Finetune 流程:我们首先从大量的有标签数据上进行训练,得到预训练的模型,然后对于新的下游任务(Downstream task),我们将学习到的参数进行迁移,在新的有标签任务上进行「微调」,从而得到一个能适应新任务的网络。
自监督的 Pretrain - Finetune 流程:
首先从大量的无标签数据中通过 pretext
来训练网络,得到预训练的模型,然后对于新的下游任务,和监督学习一样,迁移学习到的参数后微调即可。所以自监督学习的能力主要由下游任务的性能来体现
。 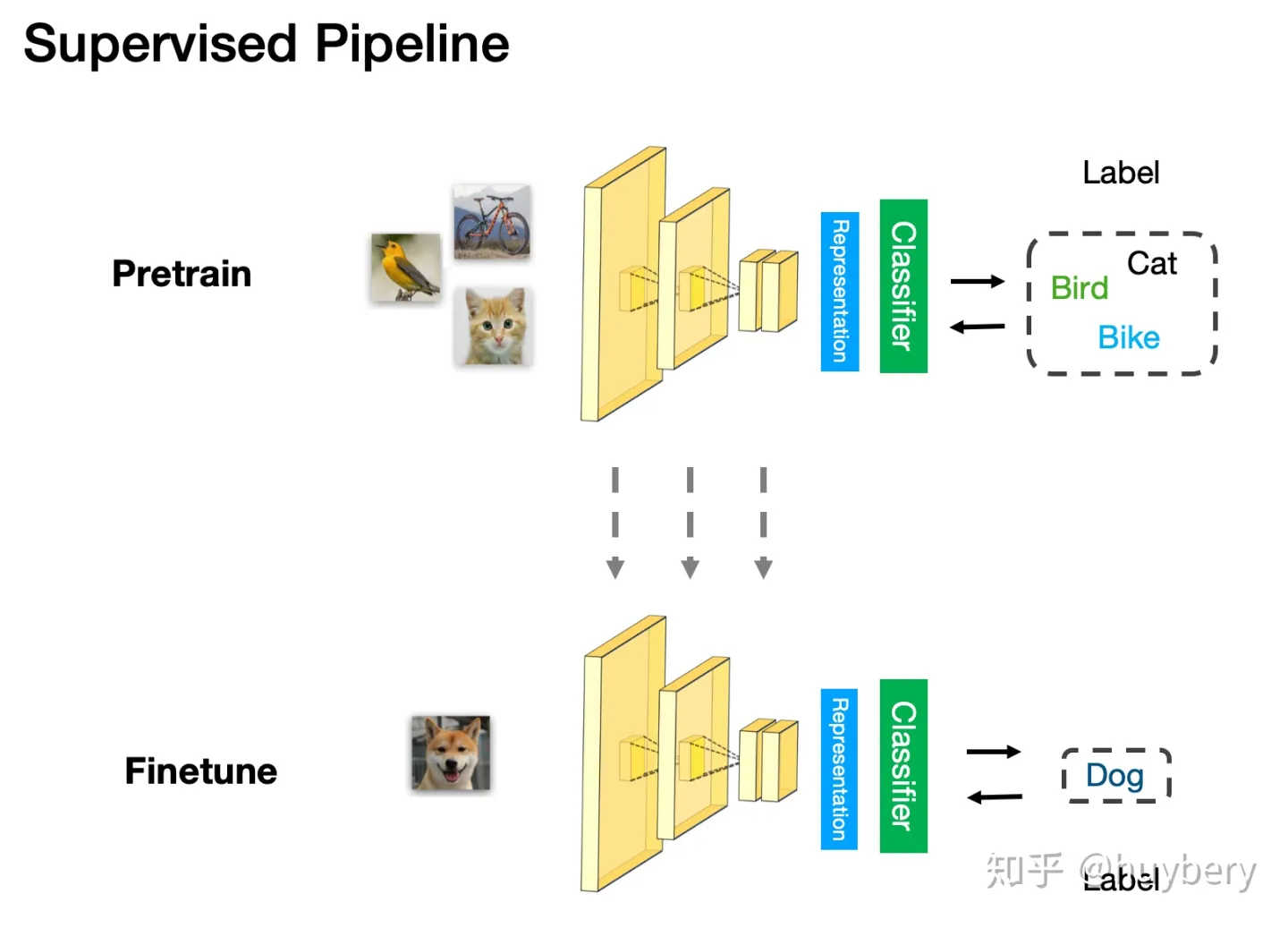
监督学习的 Pretrain-Finetune 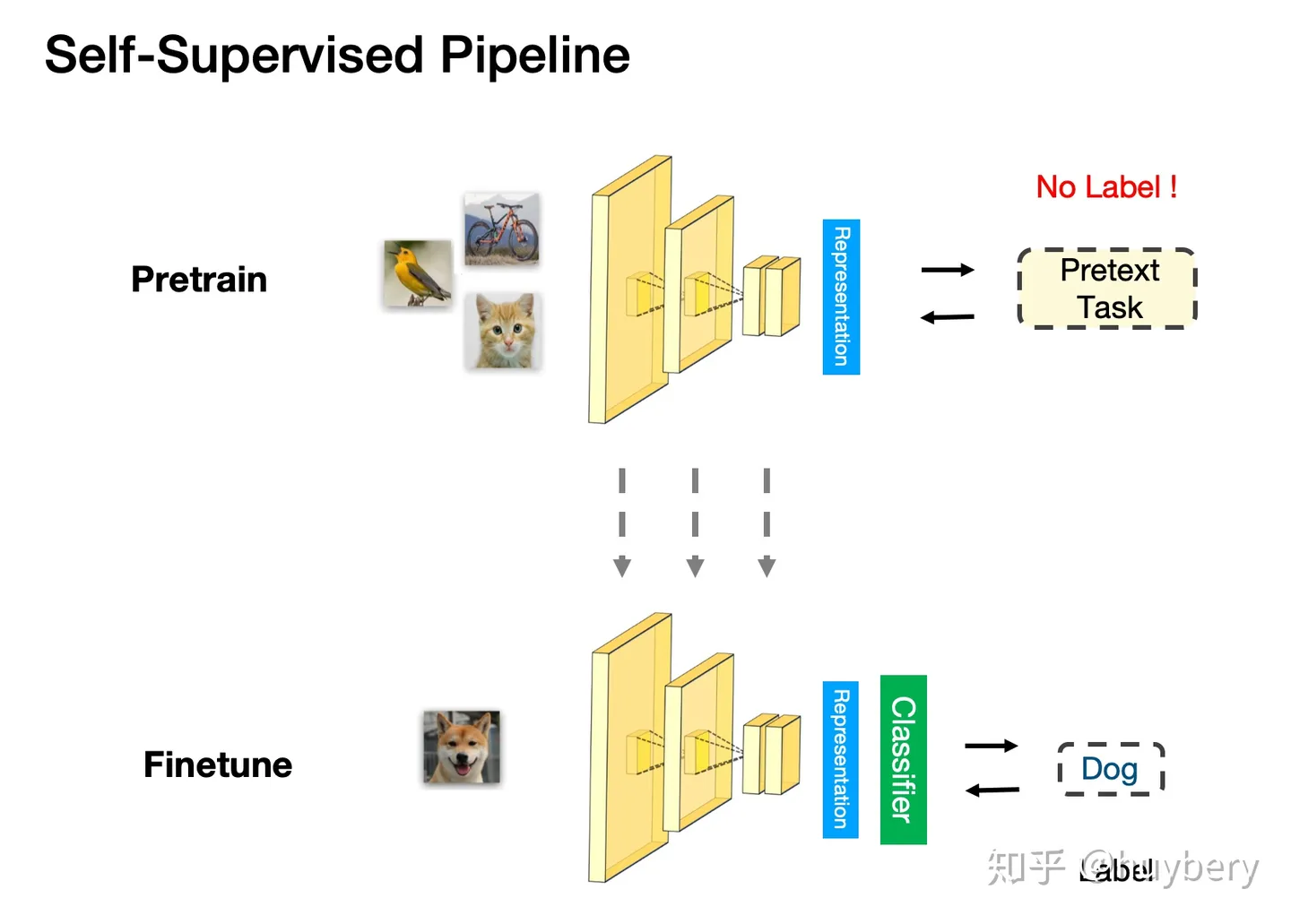
3 、自监督的学习方法
自监督学习的方法主要可以分为 3 类:1. 基于上下文(Context based) 2. 基于时序(Temporal Based)3. 基于对比(Contrastive Based)
3.1 基于上下文
context-based中文就是基于上下文的自监督学习。这也是早期自监督模型设计的主要思路方法。这部分内容将通过几篇极具代表性的文章进行讲解。
基于数据本身的上下文信息,我们其实可以构造很多任务,比如在 NLP 领域中最重要的算法 Word2vec 。 Word2vec 主要是利用语句的顺序,例如 CBOW 通过前后的词来预测中间的词,而 Skip-Gram 通过中间的词来预测前后的词。
本身是自然语言的处理方式,通过此思想引入到图像领域。
1. 拼图
[1] Carl Doersch, Abhinav Gupta, and Alexei A Efros. “Unsupervised visual representation learning by context prediction”. In: Proceedings of the IEEE international conference on computer vision. 2015, pp. 1422–1430.
首先是一篇发布于ICCV 2015[1]上利用图片色块(patch)相对位置预测进行预训练的自监督模型。具体的方法如下所示:
将一张图分成 9
个部分,然后通过预测这几个部分的相对位置来产生损失 ,比如我们
输入这张图中的小猫的眼睛和右耳朵,期待让模型学习到猫的右耳朵是在脸部的右上方的
,如果模型能很好的完成这个任务,那么我们就可以认为模型学习到的表征是具有语义信息的。
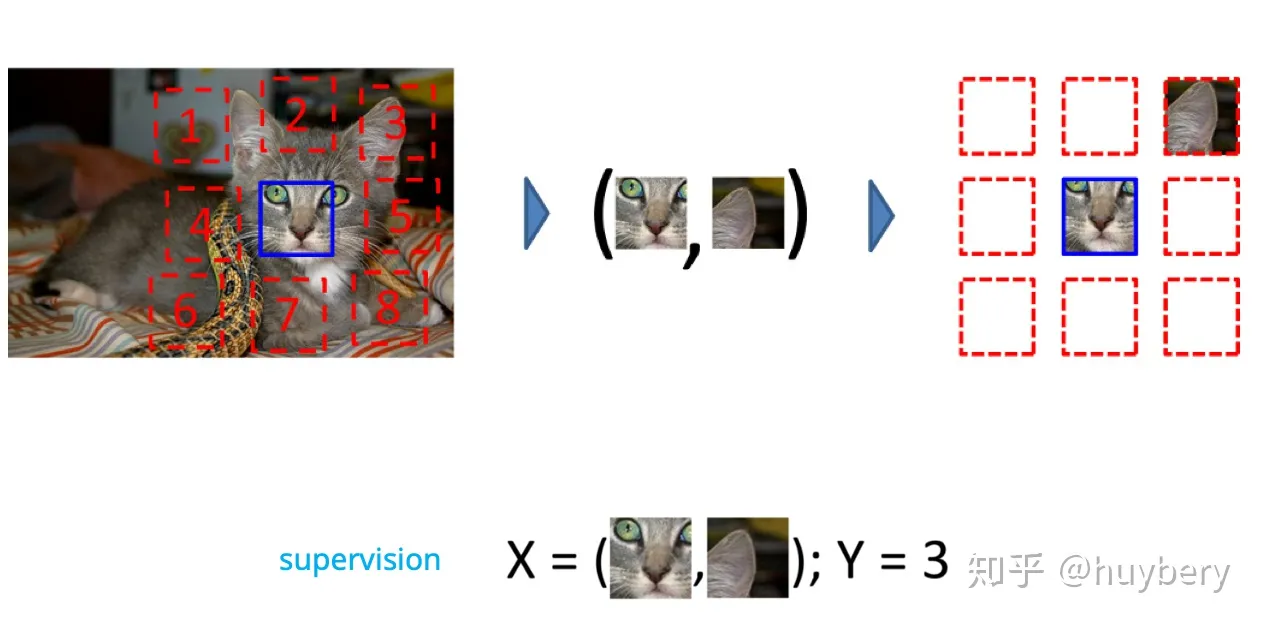
在给定一个色块后,为周围8个色块分别打上1-8的位置“伪标签”。预训练需要做的是预测随机选取的第二个色块所对应的数字。如例子所示,第二个色块选取了右边的猫耳,模型训练后给出了相对位置3。为了学习到高级的语义信息(物体层次的特征属性等,而不是颜色,质地,形状等低级语义),在进行色块选取的时候还采用了以下的操作:
- 色块与色块之间存在一定的距离,约为色块宽度的一半。这样做的目的是避免边缘信息提供相对位置之间的暗示。
- 随机抖动色块的位置使其偏移7个像素。从上图可以看出,每个色块并不是整齐排列的,他们或左或右,或上或下有些偏移。
- 对图片进行color dropping 或者添加高斯噪声防止色差的影响。
预训练的模型采用的是AlexNet为基础的架构,采用的是parallel的形式,具体如图:
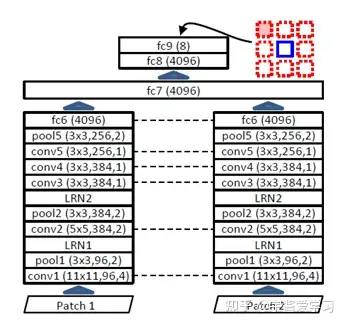
在第6个全连接层(fc)后将两个网络结合到一起变成一个更大的全连接层。之后的输出是一个8个单元的向量,进行位置判断。
在应用在下游任务前,作者还对这个网络学习到的表征和有监督学习和传统无监督学习进行了对比:

这个evaluation采用了nearest neighbors的方法,计算了每个图片的embedding,然后通过embedding的相似程度去寻找与输入最近的图片,进行聚类。通过这个方法,可以一定程度上衡量网络学习到的表征信息。从上图可以看出,三种方法中,随机初始化的效果最差,而自监督和有监督旗鼓相当,效果都不错。
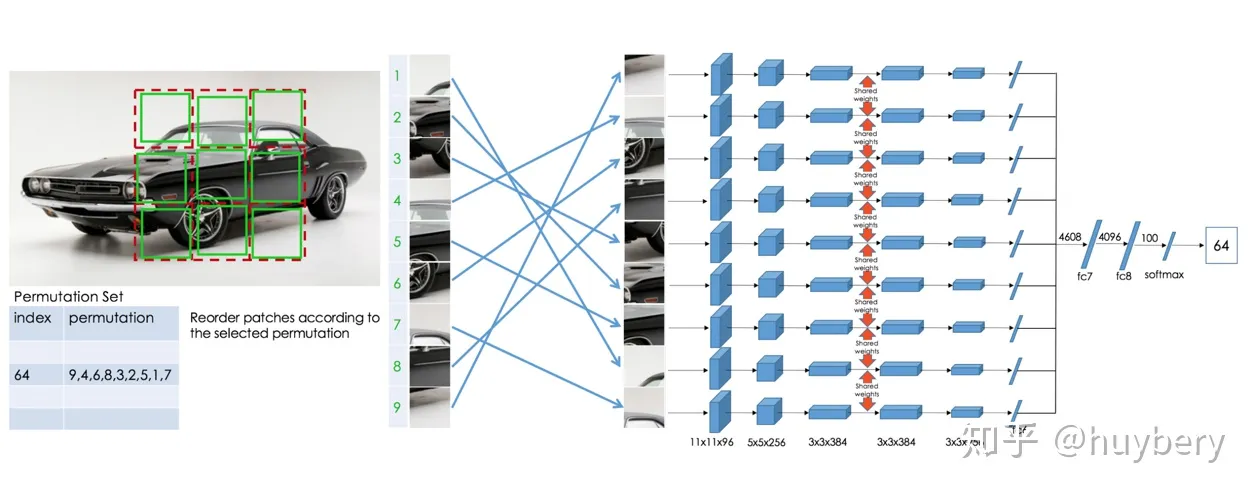
后续的工作[8]人们又拓展了这种拼图的方式,设计了更加复杂的,或者说更难的任务。
- 首先我们依然将图片分为 9 块,我们预先定义好 64 种排序方式。
- 模型输入任意一种被打乱的序列,期待能够学习到这种序列的顺序属于哪个类。
上个工作相比,这个模型需要学习到更多的相对位置信息。这个工作带来的启发就是使用更强的监督信息,或者说辅助任务越难,最后的性能越好。
2.抠图
Features learning by inpainting
[2] Deepak Pathak et al. “Context encoders: Feature learning by inpainting”. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2016, pp. 2536–2544.
随机的将图片中的一部分删掉,然后利用剩余的部分来预测扣掉的部分,只有模型真正读懂了这张图所代表的含义,才能有效的进行补全
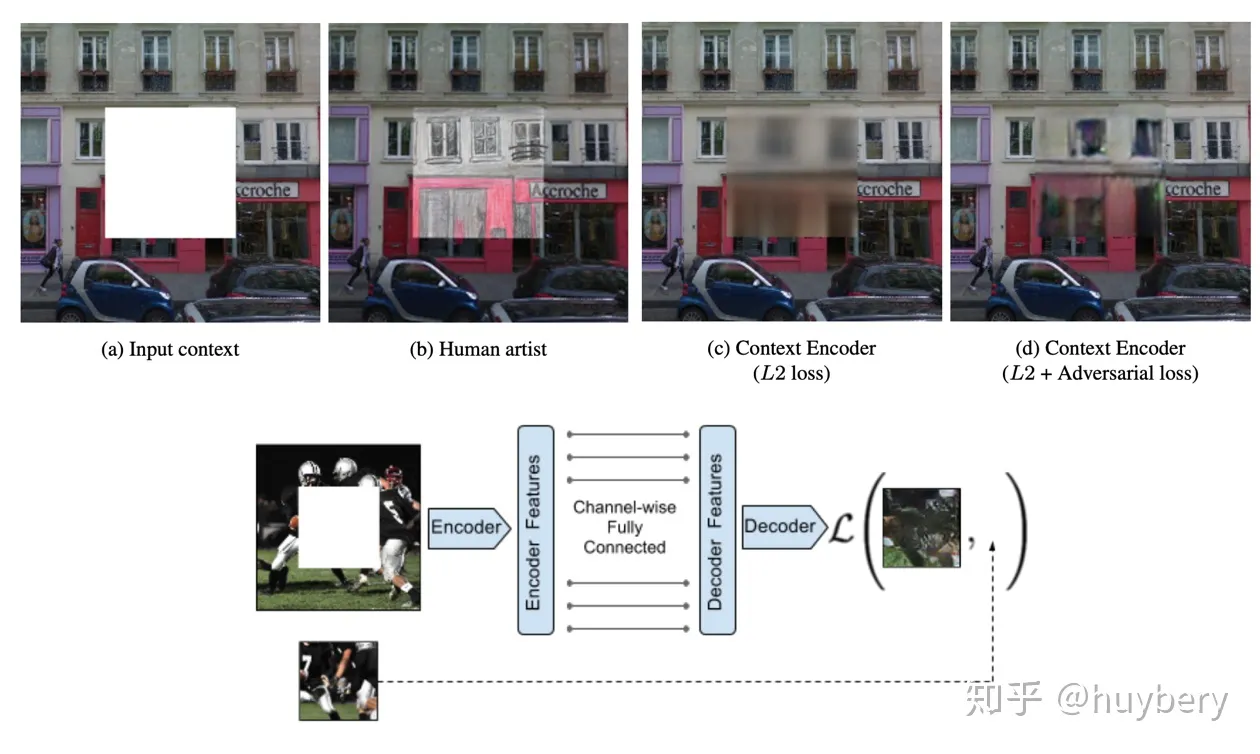
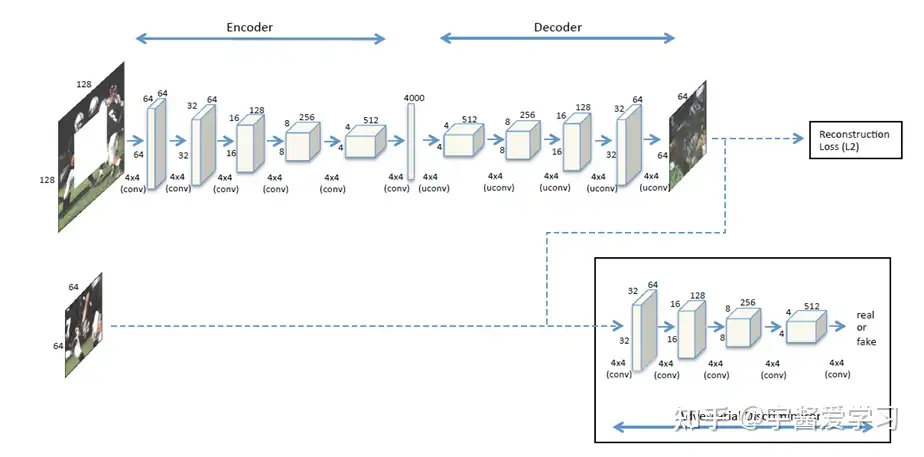
在这个网络架构中使用了两种函数,一个是重构损失L2,衡量了encoder-decoder阶段生成的图片与真实缺块间的距离。可以用下面的公式表示:

此外,辨别器(discriminator)需要判断生成的图片能否通过检测,因此需要一个对抗损失(adversarial
loss),在这里只提取了GAN损失函数中discriminator的部分: 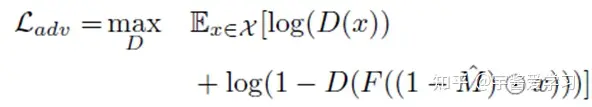
判别器的作用就是尽量分辨图片的来源:是真实的还是生成的?因此,要尽可能让两者间的差距大。接着将两个损失函数通过超参数结合在一起就是最终的损失:
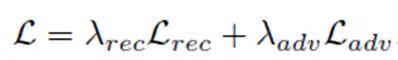
在实验中$ λ_{rec}=0.999,λ_{adv}=0.001$
此外,为了增加生成的困难度和提高模型的泛化能力,挖空的方式除了中心挖空外,还有以下几种情况:

同样,在文章中作者对encoder-decoder学习到的表征和其他算法进行了对比,结果如下:(看起来效果也不是很好啊)

可以看到,在只用了encoder-decoder而没用discriminator时,生成的缺块有点模糊;而反之只使用discriminator时生成的缺块与周围像素不匹配。因此将两者结合起来时,补全的图形与真实情况最为接近。
但是这个预训练任务也存在一些缺陷。在这篇文章[3]中指出了其中三个:
- 损失函数无法捕捉修复的质量。(Loss function may not capture inpainting quality)
- 由于下游任务的输入是完整的图片,因此在训练和测试时可能会产生domain gap的问题。(Cause a “domain gap” between training and test)
- 在预测生成缺块时主要利用的是周围的像素信息,包括颜色,形状,灰度值等,因此没有高级语义信息的应用。(Solved inpainting without high-level reasoning)
3.颜色信息
模型输入图像的灰度图,来预测图片的色彩 。只有模型可以理解图片中的语义信息才能得知哪些部分应该上怎样的颜色,比如天空是蓝色的,草地是绿色的,只有模型从海量的数据中学习到了这些语义概念,才能得知物体的具体颜色信息。同时这个模型在训练结束后就可以做这种图片上色的任务。
对于原始数据,首先分成两部分,然后通过一部分的信息来预测另一部分,最后再合成完成的数据。和传统编码器不同的是,这种预测的方式可以促使模型真正读懂数据的语义信息才能够实现,所以相当于间接地约束编码器不单单靠
pixel-wise 层面来训练,而要同时考虑更多的语义信息 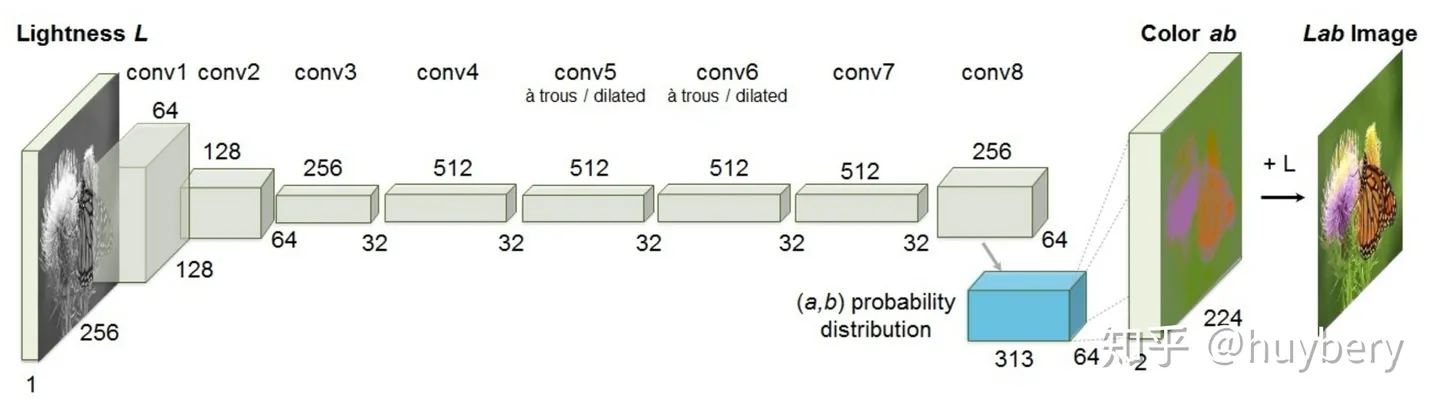
4.数据增广
给定一张输入的图片,我们对其进行不同角度的旋转,模型的目的是预测该图片的旋转角度 。
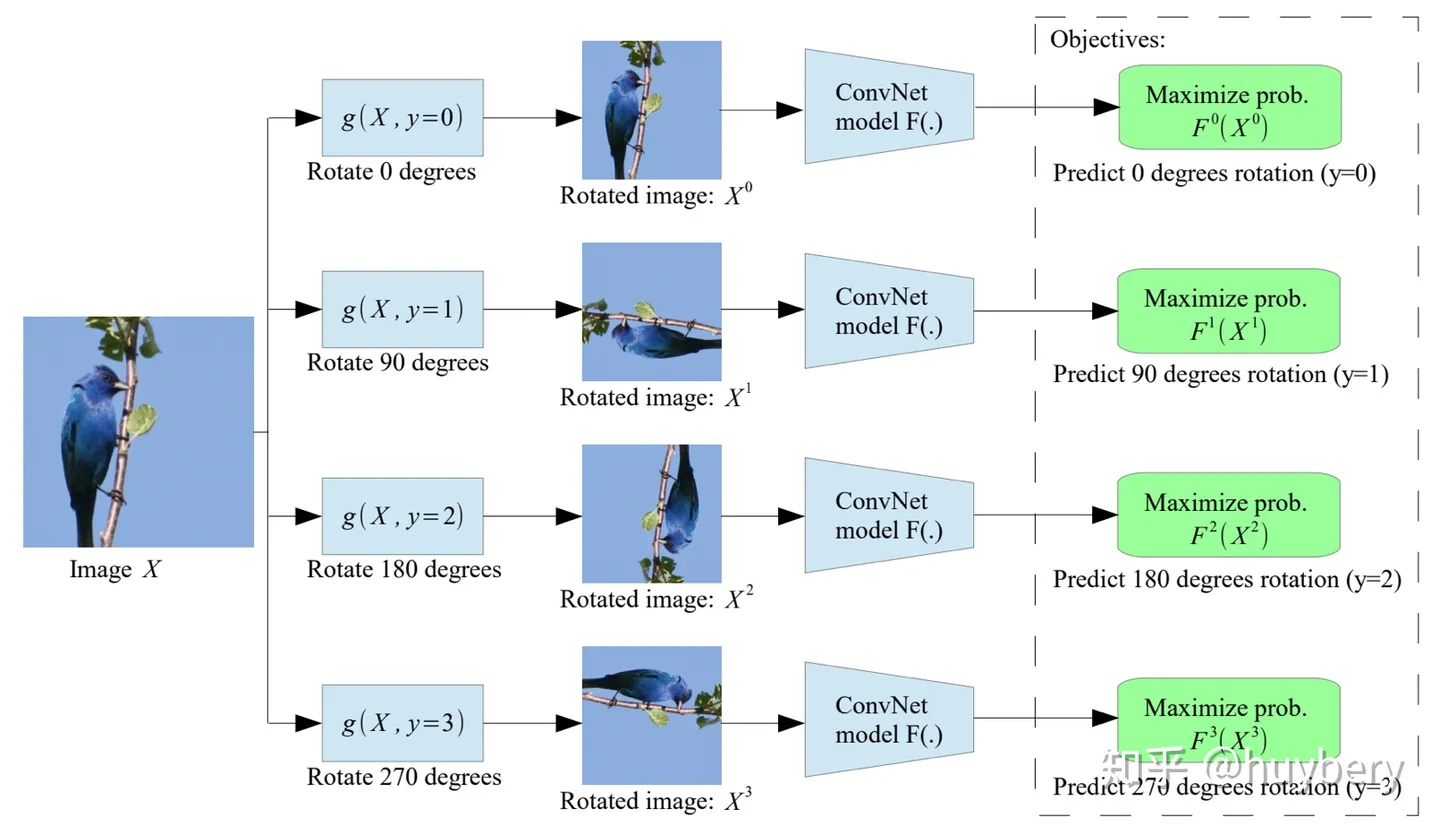
文章中还出现了自监督和有监督学习first layer filters的比较:

可以看到,自监督的结果主要是各种频率的定向边缘过滤器。并且,相比有有监督学习,自监督增加了旋转角度的预测,因此有更多的种类。
3.2.基于时序
之前介绍的方法大多是基于样本自身的信息,比如旋转、色彩、裁剪等。而样本间其实也是具有很多约束关系的,这里我们来介绍利用时序约束来进行自监督学习的方法。最能体现时序的数据类型就是视频了(video)。
1.相邻特征相似性
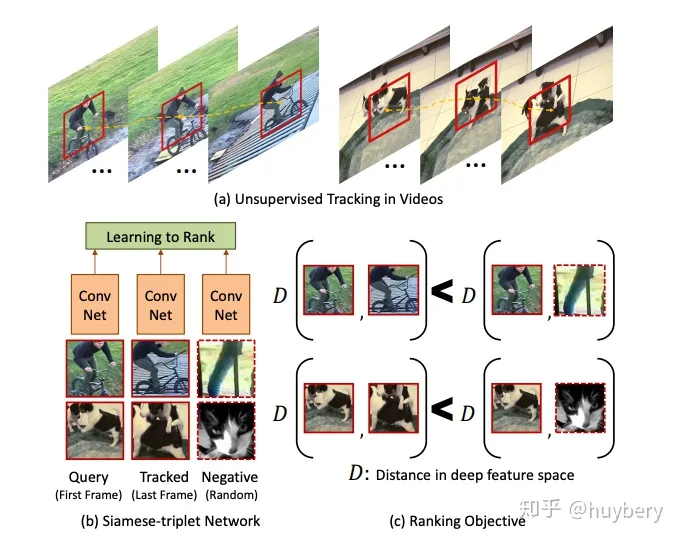
视频中的相邻帧特征是相似的,而相隔较远的视频帧是不相似的,通过构建这种相似(position)和不相似(negative)的样本来进行自监督约束
2.多视角相似性
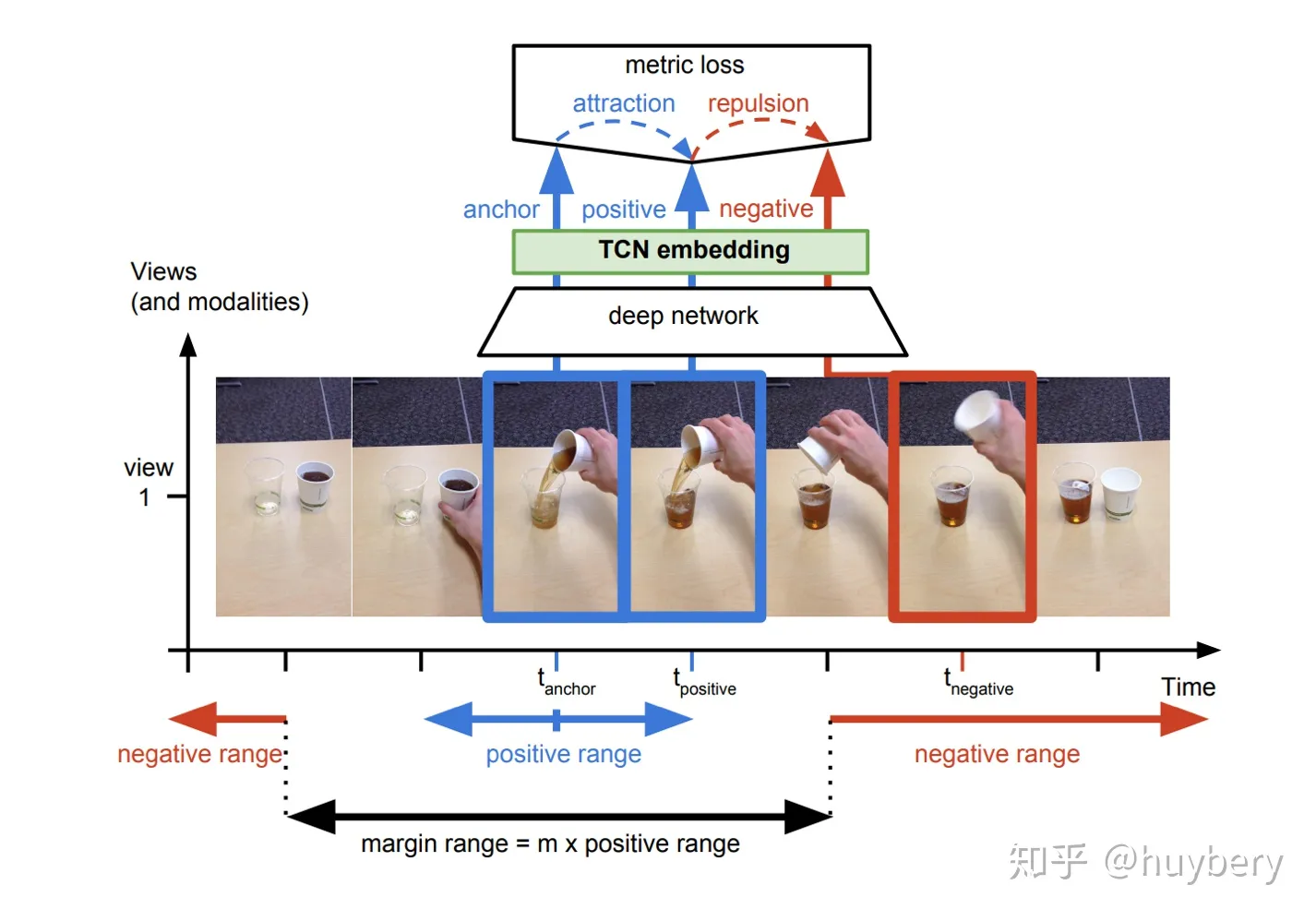
对于同一个物体的拍摄是可能存在多个视角(multi-view),对于多个视角中的同一帧,可以认为特征是相似的,对于不同帧可以认为是不相似的 。
基于顺序的约束还被应用了到了对话系统中,ACL 2019 [20] 提出的自监督对话学习就是基于这种思想。这篇文章主要是想解决对话系统中生成的话术连贯性的问题,期待机器生成的回复和人类交谈一样是符合之前说话的风格、习惯等等。从大量的历史预料中挖掘出顺序的序列(positive)和乱序的序列(negative),通过模型来预测是否符合正确的顺序来进行训练。训练完成后就拥有了一个可以判断连贯性的模型,从而可以嵌入到对话系统中,最后利用对抗训练的方式生成更加连贯的话术。
3.基于对比
介绍的基于时序的方法已经涉及到了这种基于对比的约束, 通过构建正样本(positive)和负样本(negative),然后度量正负样本的距离来实现自监督学习 。核心思想样本和正样本之间的相似度远远大于样本和负样本之间的相似度。
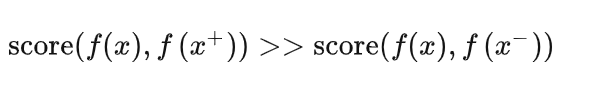
这里的 x 通常也称为 「anchor」数据,为了优化 anchor 数据和其正负样本的关系,我们可以使用点积的方式构造距离函数,然后构造一个 softmax 分类器,以正确分类正样本和负样本。
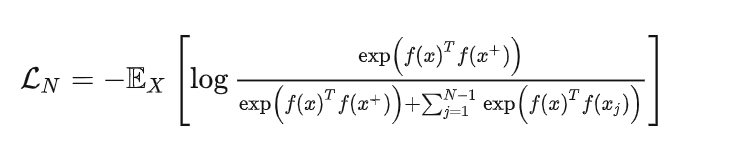
这个损失也被称为 InfoNCE,后面的所有工作也基本是围绕这个损失进行的。
对比学习和之前提到的生成学习有什么区别呢?

区别主要在两个方面:
- 损失计算的空间不同。生成或者预测类方法损失是在输出空间计算的;而对比方法的损失是在表征空间计算的。
- 对比方法有对相关性或复杂结构进行建模的能力,而不仅仅像生成方法一样基于像素进行特征学习。
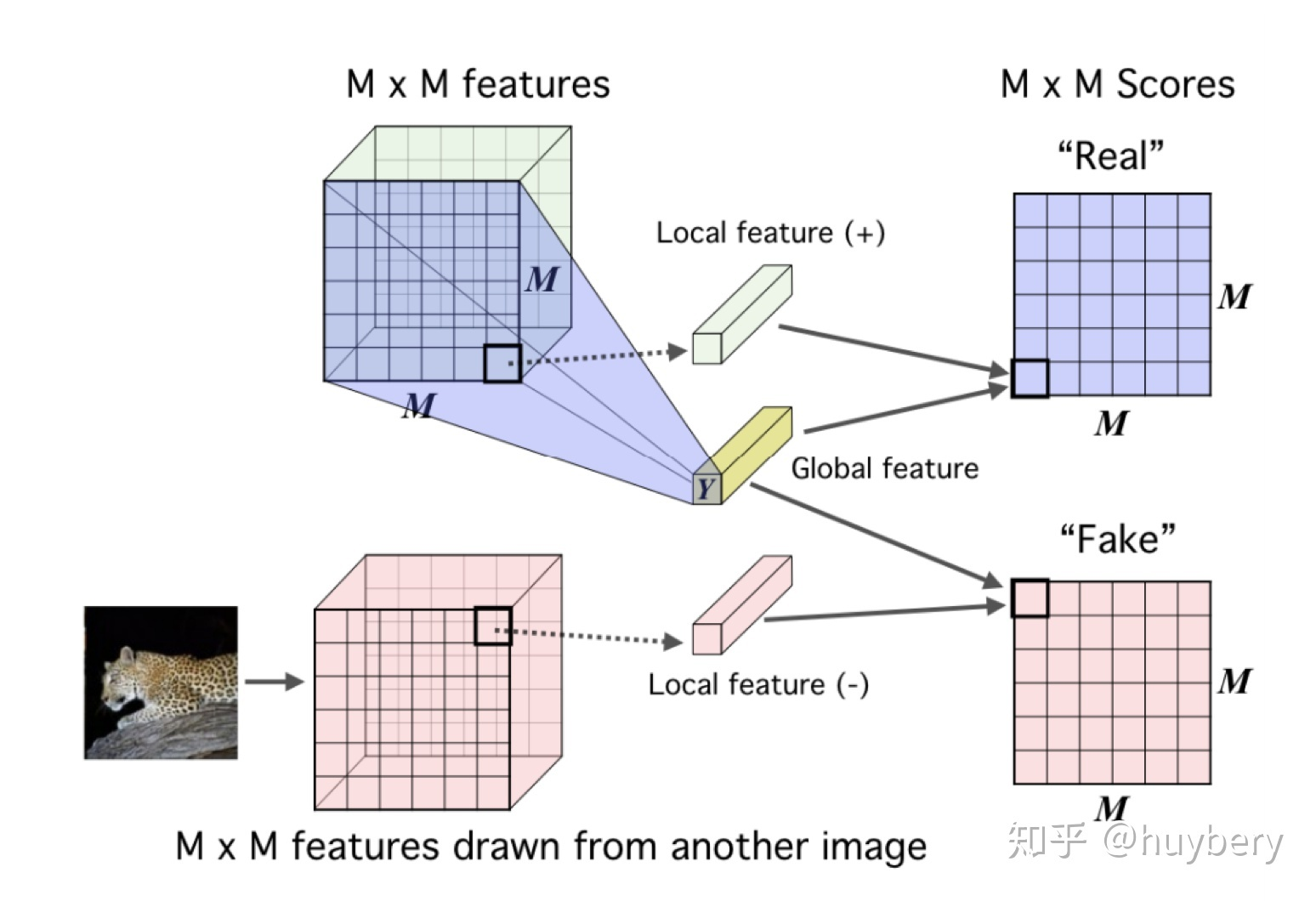
DIM
DIM 的具体思想是对于隐层的表达,对不同的图片用卷积encoder进行表征的提取,encoder最终的输出为全局的特征(global features);而中间层的输出为本地特征(local features), 模型需要分类全局特征和局部特征是否来自同一图像 。所以这里 x 是来自一幅图像的全局特征,正样本是该图像的局部特征,而负样本是其他图像的局部特征。
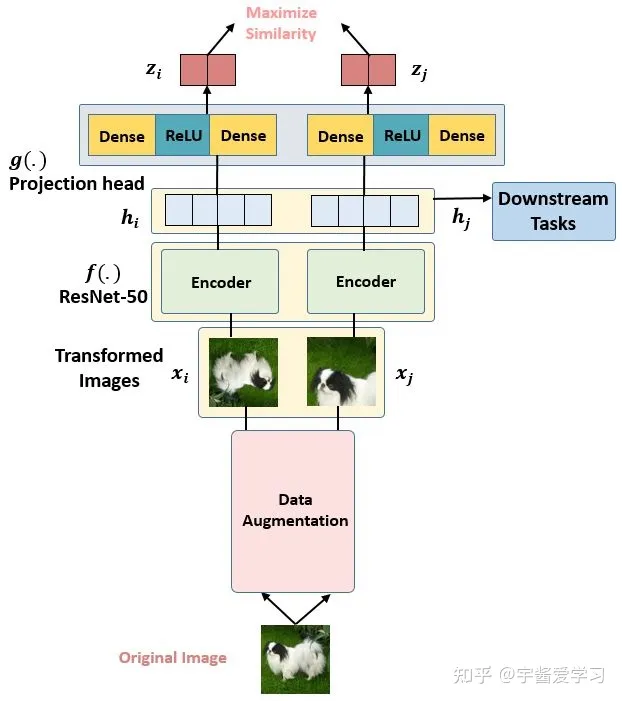
SimCLR
SimCLR
V1是Hitom团队在2020年时提出的一种针对视觉的对比自监督模型。后续文章会详细讲解
4、展望
自监督学习分类示意图 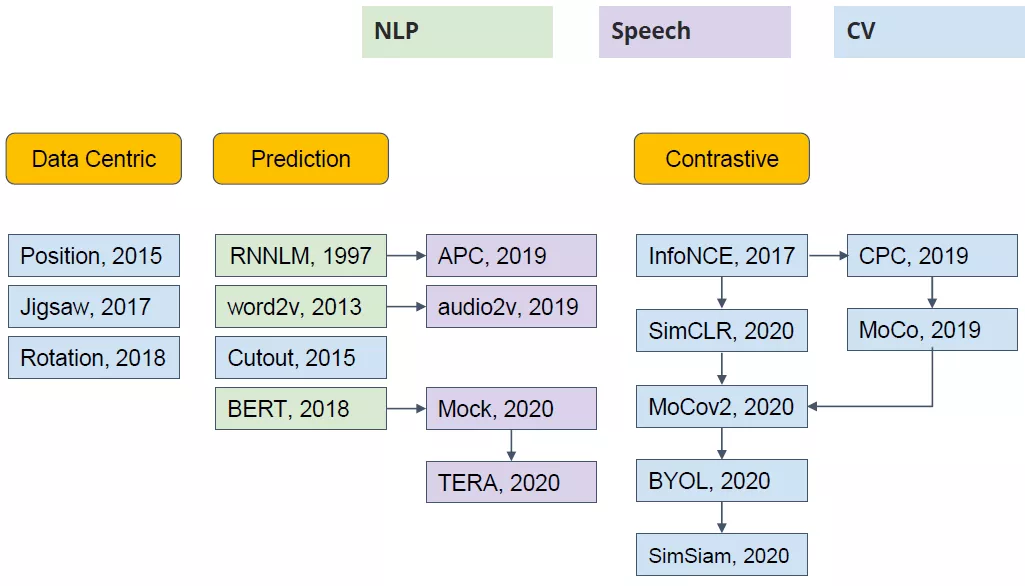
自监督学习在预训练模型中的成功让研究人员觉得非常兴奋,同时也激发了更多的灵感。越来越多的工作开始思考自监督学习和具体任务紧密结合的方法(Task
Related Self-Supervised Learning) 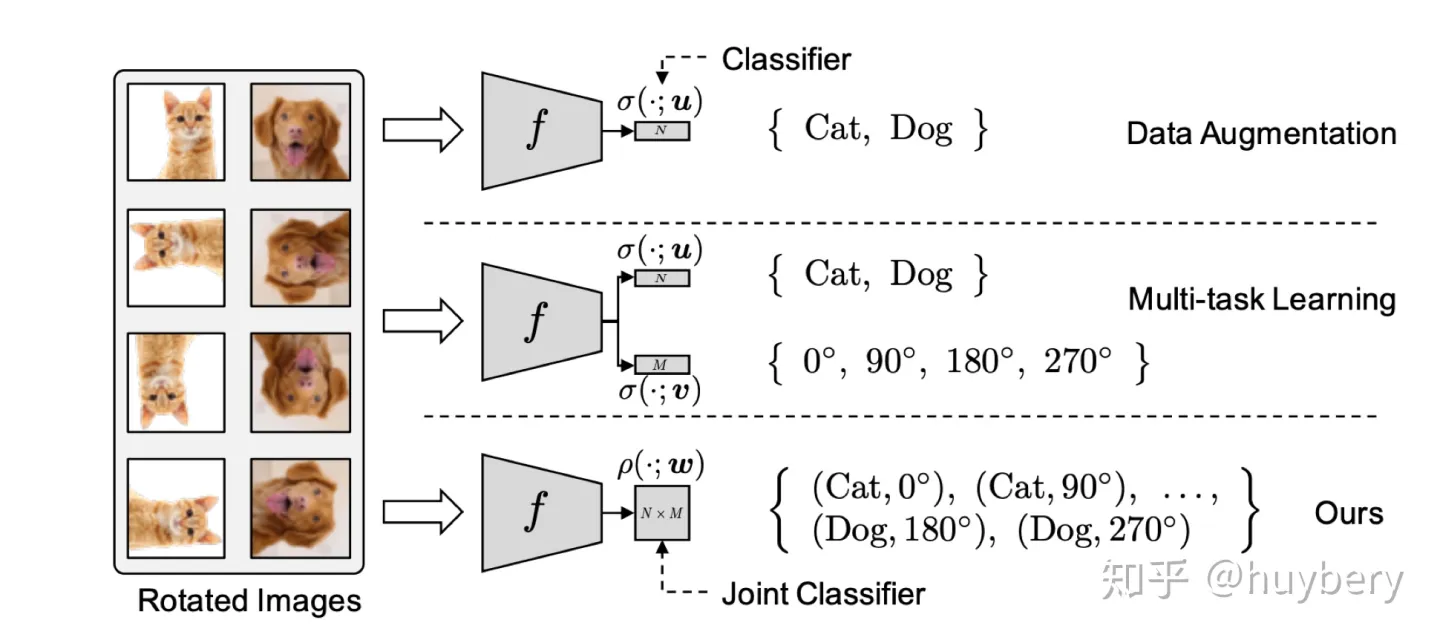
Lee, Hankook et al
[14]探索了在多任务学习中增加自监督学习的可能,他们将普通的分类任务中嵌入了旋转预测任务。除了简单的多任务学习,也可以设计联合学习策略,直接预测两种监督信息。同样的想法也被用到了小样本学习[15]中,一个分支进行传统的小样本分类,另一个分支来进行自监督旋转预测,虽然这篇文章的想法和设计不是很亮眼,但提升还是比较明显的。
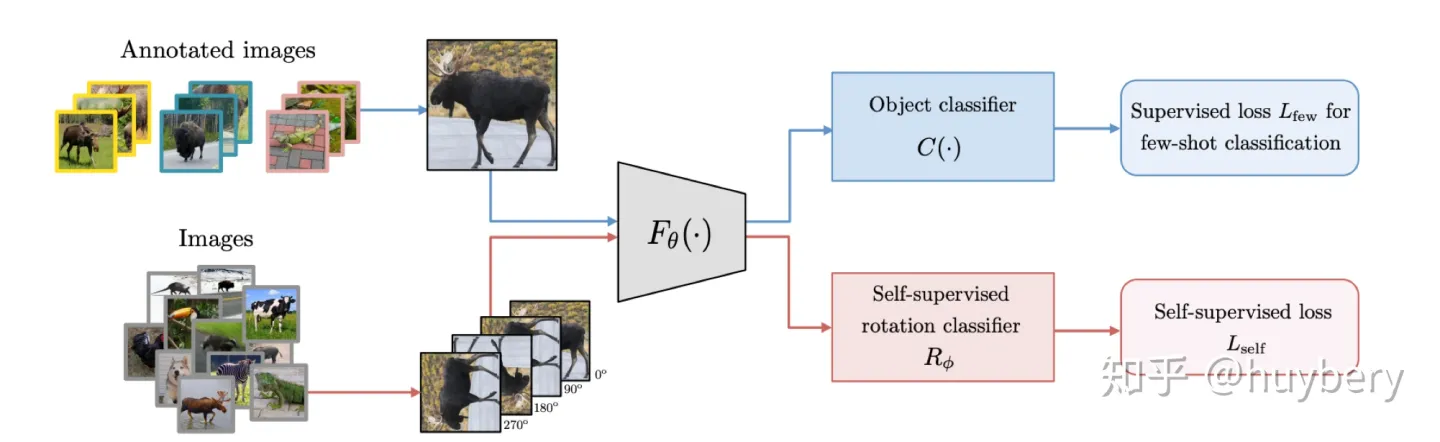
而自监督和半监督学习[16]也可以进行结合,对于无标记的数据进行自监督学习(旋转预测),和对于有标记数据,在进行自监督学习的同时利用联合训练的想法进行有监督学习
Lee, Hankook et al [14]探索了在多任务学习中增加自监督学习的可能,他们将普通的分类任务中嵌入了旋转预测任务。除了简单的多任务学习,也可以设计联合学习策略,直接预测两种监督信息。同样的想法也被用到了小样本学习[15]中,一个分支进行传统的小样本分类,另一个分支来进行自监督旋转预测,虽然这篇文章的想法和设计不是很亮眼,但提升还是比较明显的。
可变形卷积
提出背景¶
视觉识别的一个关键挑战是如何适应物体尺度、姿态、视点和零件变形的几何变化或模型几何变换。
但对于视觉识别的传统CNN模块,不可避免的都存在固定几何结构的缺陷:卷积单元在固定位置对输入特征图进行采样;池化层以固定比率降低空间分辨率;一个ROI(感兴趣区域)池化层将一个ROI分割成固定的空间单元;缺乏处理几何变换的内部机制等。
这些将会引起一些明显的问题。例如,同一CNN层中所有激活单元的感受野大小是相同的,这对于在空间位置上编码语义的高级CNN层是不需要的。而且,对于具有精细定位的视觉识别(例如,使用完全卷积网络的语义分割)的实际问题,由于不同的位置可能对应于具有不同尺度或变形的对象,因此,尺度或感受野大小的自适应确定是可取的。
为了解决以上所提到的局限性,一个自然地想法就诞生了: 卷积核自适应调整自身的形状 。这就产生了可变形卷积的方法。
可变形卷积¶
DCN v1¶
可变形卷积顾名思义就是卷积的位置是可变形的,并非在传统的𝑁×𝑁N×N的网格上做卷积,这样的好处就是更准确地提取到我们想要的特征(传统的卷积仅仅只能提取到矩形框的特征),通过一张图我们可以更直观地了解:
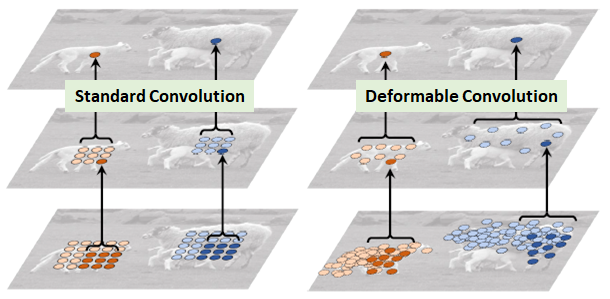
图1 绵羊特征提取
在上面这张图里面,左边传统的卷积显然没有提取到完整绵羊的特征,而右边的可变形卷积则提取到了完整的不规则绵羊的特征。
那可变卷积实际上是怎么做的呢?
其实就是在每一个卷积采样点加上了一个偏移量 ,如下图所示: 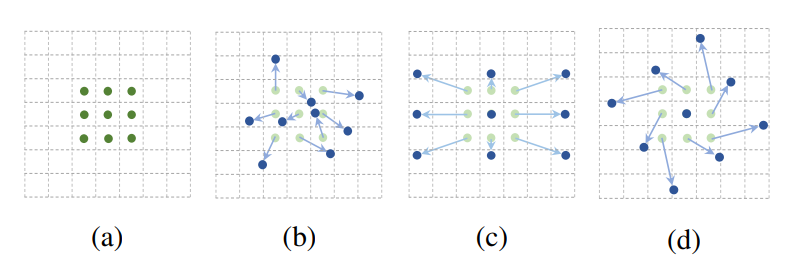
图2 卷积核和可变形卷积核

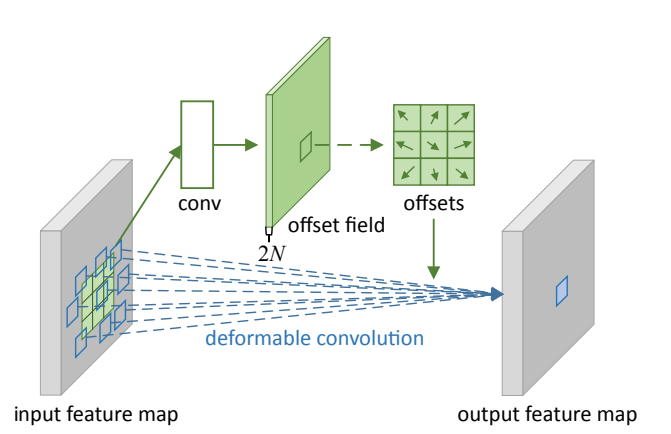

DCN v2

paddle中的API
1 | paddle.vision.ops.deform_conv2d(*x*, *offset*, *weight*, *bias=None*, *stride=1*, *padding=0*, *dilation=1*, *deformable_groups=1*, *groups=1*, *mask=None*, *name=None*); |
deform_conv2d 对输入4-D Tensor计算2-D可变形卷积。详情参考deform_conv2d。

算法实例:
1 | #deformable conv v2: |

实例效果¶
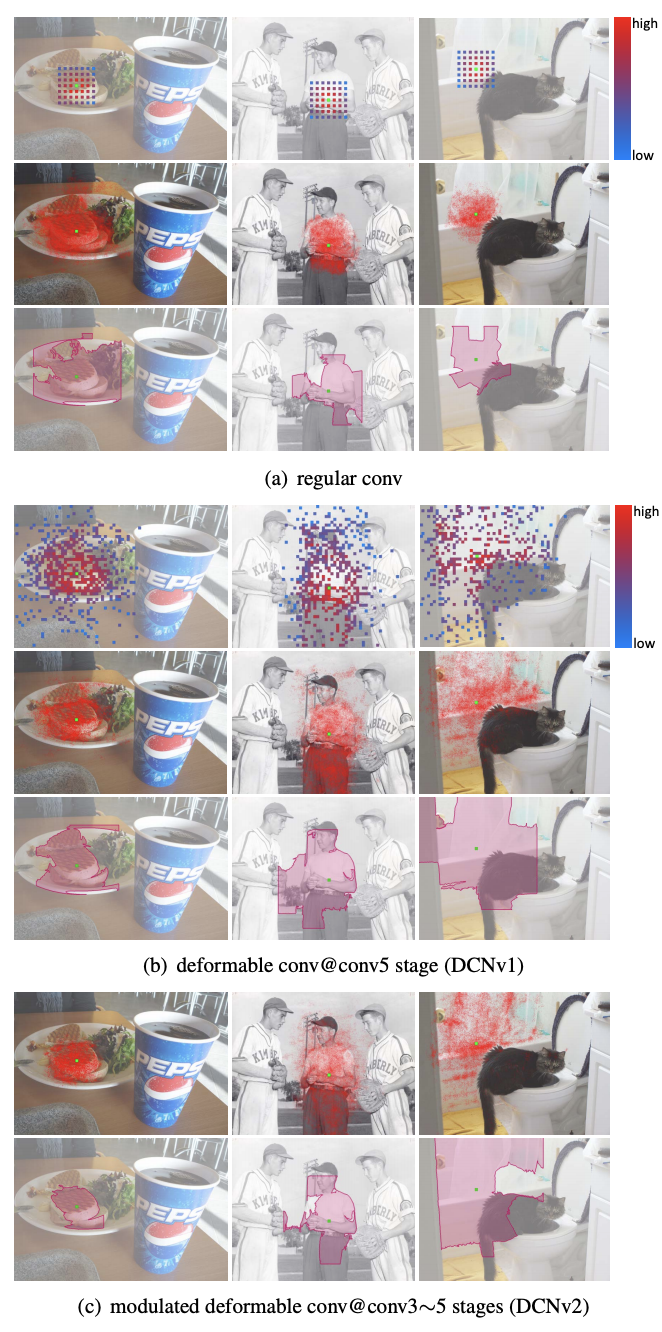
图4 regular、DCN v1、DCN v2的感受野对比

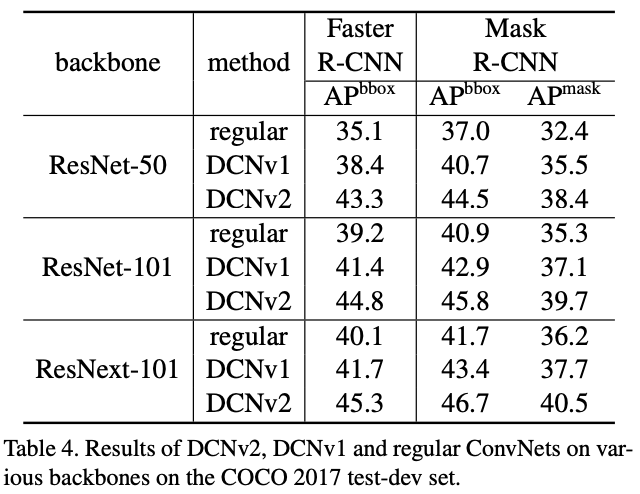
图5 regular、DCN v1、DCN v2的准确率对比

多层感知机
多层感知机(Multilayer Perceptron,MLP)是一种前馈人工神经网络模型。
一、结构组成
- 输入层:接收输入数据,输入层的神经元数量通常与输入数据的特征数量相对应。例如,如果输入的是一幅图像,输入层的神经元数量可以是图像的像素数量或者经过特征提取后的特征向量的维度。
- 隐藏层:位于输入层和输出层之间,可以有一个或多个隐藏层。每个隐藏层由多个神经元组成,这些神经元通过权重与上一层的神经元连接。隐藏层的作用是对输入数据进行非线性变换,提取更高级别的特征。
- 输出层:产生最终的输出结果,输出层的神经元数量通常与任务的输出维度相对应。例如,在分类任务中,输出层的神经元数量可以是类别数量;在回归任务中,输出层通常只有一个神经元,输出一个连续的值。
二、工作原理
信号传播:
- 前向传播:数据从输入层进入网络,通过各层之间的连接权重进行加权求和,然后经过激活函数的非线性变换,传递到下一层。这个过程在每个隐藏层和输出层中重复,直到得到最终的输出结果。
- 反向传播:在训练过程中,根据输出结果与真实标签之间的误差,通过反向传播算法调整网络中的连接权重。反向传播算法从输出层开始,计算每个神经元的误差梯度,并将误差梯度反向传播到上一层,依次调整各层的连接权重,以减小误差。
激活函数:
- 作用:在每个神经元中,加权求和的结果经过激活函数进行非线性变换。激活函数的作用是引入非线性因素,使网络能够学习和表示复杂的函数关系。常见的激活函数有 Sigmoid 函数、ReLU 函数、Tanh 函数等。
- 不同激活函数的特点:
- Sigmoid 函数:将输入值压缩到 0 到 1 之间,具有平滑的曲线,在早期的神经网络中广泛使用。但在输入值较大或较小时,函数的梯度趋近于零,容易导致梯度消失问题。
- ReLU 函数:对于正输入值,输出等于输入;对于负输入值,输出为零。ReLU 函数计算简单,能够有效地缓解梯度消失问题,并且在训练过程中收敛速度较快。
- Tanh 函数:将输入值压缩到 -1 到 1 之间,具有类似 Sigmoid 函数的形状,但在输入值较大或较小时,梯度变化比 Sigmoid 函数更平缓,一定程度上缓解了梯度消失问题。
三、应用领域
- 分类任务:MLP 可以用于图像分类、文本分类、语音识别等领域。通过学习输入数据的特征表示,MLP 能够将输入数据划分到不同的类别中。
- 回归任务:在预测连续值的任务中,如房价预测、股票价格预测等,MLP 可以通过学习输入数据与输出值之间的函数关系,进行回归分析。
- 模式识别:MLP 可以识别和提取输入数据中的模式和特征,例如在手写数字识别、人脸识别等任务中,MLP 能够学习到数字或人脸的特征表示,实现准确的识别。
总之,多层感知机是一种强大的人工神经网络模型,通过多个神经元组成的层次结构和非线性激活函数,能够学习和表示复杂的函数关系,在各种机器学习任务中得到了广泛的应用。
分类问题所使用的指标
准确率
简单来说就是计算一个批次数据中 true 的数量占总的数量

混淆矩阵的定义
对于二分类问题,混淆矩阵是一个2x2的矩阵,如下所示:
预测为正类 预测为负类实际为正类 TP FN 实际为负类 FP TN
- TP(True Positive):被正确预测为正类的样本数。
- FN(False Negative):被错误预测为负类的正类样本数。
- FP(False Positive):被错误预测为正类的负类样本数。
- TN(True Negative):被正确预测为负类的样本数。
对于多分类问题,混淆矩阵是一个nxn的矩阵,其中n是类别的数量。
混淆矩阵的示例
假设有一个二分类问题,模型预测的结果如下:
实际为正类的样本有100个,其中被正确预测为正类的有80个,被错误预测为负类的有20个。
实际为负类的样本有200个,其中被错误预测为正类的有30个,被正确预测为负类的有170个。
预测为正类 预测为负类 实际为正类 80 20 实际为负类 30 170
对于多分类问题,混淆矩阵是一个nxn的矩阵,其中n是类别的数量。矩阵的行表示实际类别,列表示预测类别。例如,对于一个三分类问题,混淆矩阵可能如下所示:
1 | 预测为类别1 预测为类别2 预测为类别3 |
- TP1、TP2、TP3分别表示被正确预测为类别1、类别2、类别3的样本数。
- FP12、FP13、FP21、FP23、FP31、FP32分别表示被错误预测为类别1、类别2、类别3的样本数。
召回率
输入为混淆矩阵

召回率是分类问题中衡量模型性能的一个重要指标,它表示被正确分类为正例的样本占所有实际正例样本的比例。
混淆矩阵是一个二维数组,用于描述分类模型在测试集上的表现。矩阵的行表示实际类别,列表示预测类别。例如,如果混淆矩阵是
1 | [[TP, FN], |
其中,TP(True Positive)表示被正确分类为正例的样本数,FN(False Negative)表示被错误分类为负例的正例样本数,FP(False Positive)表示被错误分类为正例的负例样本数,TN(True Negative)表示被正确分类为负例的样本数。
计算召回率
:函数首先计算混淆矩阵对角线上的元素(即TP和TN)占每一行(即实际类别)的和的比例。这里使用了
np.diag(confusionMatrix)来获取混淆矩阵对角线上的元素,confusionMatrix.sum(axis=1)计算每一行的和。为了避免除以零的情况,代码中使用了
1e-8作为分母的一个小值。
返回结果 :函数返回一个数组,其中每个元素表示对应类别的召回率。
Recall函数主要用于评估分类模型的性能,特别是在正负样本不平衡的情况下。通过计算每个类别的召回率,可以了解模型在识别正例样本方面的表现。
精确率
精确率是分类问题中衡量模型预测为正类(positive class)的样本中实际为正类的比例。下面是对代码的详细解释:
np.diag(confusionMatrix):提取混淆矩阵的对角线元素,这些元素表示模型正确预测为正类的样本数。confusionMatrix.sum(axis = 0):计算混淆矩阵在列方向(axis=0)上的和,即每一列的和,这些和表示模型预测为正类的样本总数。+1e-8:为了避免除以零的情况,给分母加上一个极小值。np.diag(confusionMatrix) / (confusionMatrix.sum(axis = 0)+1e-8):计算精确率,即对角线元素(正确预测为正类的样本数)除以列和(预测为正类的样本总数)。

F1分数
F1分数是精确度(Precision)和召回率(Recall)的调和平均数,常用于评估分类模型的性能
F1分数的值介于0和1之间,值越大,表示模型的性能越好。
F1分数计算公式为:2 * 精确度 * 召回率 / (精确度 + 召回率)

F1分数的优点在于,它同时考虑了精确度和召回率,避免了单一指标可能带来的误导。例如,如果一个模型在正类样本上具有很高的召回率,但在负类样本上具有很低的精确度,那么这个模型可能仍然具有很高的F1分数,因为精确度和召回率的平衡点被考虑在内。
随机森林
1.什么是随机森林
1.1 Bagging思想
Bagging是bootstrap aggregating。思想就是从总体样本当中随机取一部分样本进行训练,通过多次这样的结果,进行投票获取平均值作为结果输出,这就极大可能的避免了不好的样本数据,从而提高准确度。因为有些是不好的样本,相当于噪声,模型学入噪声后会使准确度不高。
举个例子 :
假设有1000个样本,如果按照以前的思维,是直接把这1000个样本拿来训练,但现在不一样,先抽取800个样本来进行训练,假如噪声点是这800个样本以外的样本点,就很有效的避开了。重复以上操作,提高模型输出的平均值。
1.2 随机森林
Random Forest(随机森林)是一种基于树模型的Bagging的优化版本,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的特点。(可以理解成三个臭皮匠顶过诸葛亮)
而同一批数据,用同样的算法只能产生一棵树,这时Bagging策略可以帮助我们产生不同的数据集。Bagging策略来源于bootstrap aggregation:从样本集(假设样本集N个数据点)中重采样选出\(N_b\)个样本(有放回的采样,样本数据点个数仍然不变为N),在所有样本上,对这n个样本建立分类器(ID3),重复以上两步m次,获得m个分类器,最后根据这m个分类器的投票结果,决定数据属于哪一类。
.
每棵树的按照如下规则生成:
- 如果训练集大小为N,对于每棵树而言,随机且有放回地从训练集中的抽取N个训练样本,作为该树的训练集;
- 如果每个样本的特征维度为M,指定一个常数m<<M,随机地从M个特征中选取m个特征子集,每次树进行分裂时,从这m个特征中选择最优的;
- 每棵树都尽最大程度的生长,并且没有剪枝过程。
一开始我们提到的随机森林中的“随机”就是指的这里的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入,使得随机森林不容易陷入过拟合,并且具有很好得抗噪能力(比如:对缺省值不敏感)。
总的来说就是随机选择样本数,随机选取特征,随机选择分类器,建立多颗这样的决策树,然后通过这几课决策树来投票,决定数据属于哪一类( 投票机制有一票否决制、少数服从多数、加权多数 )
2. 随机森林分类效果的影响因素
- 森林中任意两棵树的相关性:相关性越大,错误率越大;
- 森林中每棵树的分类能力:每棵树的分类能力越强,整个森林的错误率越低。
减小特征选择个数m,树的相关性和分类能力也会相应的降低;增大m,两者也会随之增大。所以关键问题是如何选择最优的m(或者是范围),这也是随机森林唯一的一个参数。
.
随机森林有什么优缺点
优点:
- 在当前的很多数据集上,相对其他算法有着很大的优势,表现良好。
- 它能够处理很高维度(feature很多)的数据,并且不用做特征选择(因为特征子集是随机选择的)。
- 在训练完后,它能够给出哪些feature比较重要。
- 训练速度快,容易做成并行化方法(训练时树与树之间是相互独立的)。
- 在训练过程中,能够检测到feature间的互相影响。
- 对于不平衡的数据集来说,它可以平衡误差。
- 如果有很大一部分的特征遗失,仍可以维持准确度。
缺点:
- 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合。
- 对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的。
4. 随机森林如何处理缺失值?
根据随机森林创建和训练的特点,随机森林对缺失值的处理还是比较特殊的。
- 首先,给缺失值预设一些估计值,比如数值型特征,选择其余数据的中位数或众数作为当前的估计值
- 然后,根据估计的数值,建立随机森林,把所有的数据放进随机森林里面跑一遍。记录每一组数据在决策树中一步一步分类的路径.
- 判断哪组数据和缺失数据路径最相似,引入一个相似度矩阵,来记录数据之间的相似度,比如有N组数据,相似度矩阵大小就是N*N
- 如果缺失值是类别变量,通过权重投票得到新估计值,如果是数值型变量,通过加权平均得到新的估计值,如此迭代,直到得到稳定的估计值。
其实,该缺失值填补过程类似于推荐系统中采用协同过滤进行评分预测,先计算缺失特征与其他特征的相似度,再加权得到缺失值的估计,而随机森林中计算相似度的方法(数据在决策树中一步一步分类的路径)乃其独特之处。
5. 什么是OOB?随机森林中OOB是如何计算的,它有什么优缺点?
OOB :
上面我们提到,构建随机森林的关键问题就是如何选择最优的m,要解决这个问题主要依据计算袋外错误率oob error(out-of-bag error)。
bagging方法中Bootstrap每次约有1/3的样本不会出现在Bootstrap所采集的样本集合中,当然也就没有参加决策树的建立,把这1/3的数据称为 袋外数据oob(out of bag) ,它可以用于取代测试集误差估计方法。
袋外数据(oob)误差的计算方法如下:
- 对于已经生成的随机森林,用袋外数据测试其性能,假设袋外数据总数为O,用这O个袋外数据作为输入,带进之前已经生成的随机森林分类器,分类器会给出O个数据相应的分类
- 因为这O条数据的类型是已知的,则用正确的分类与随机森林分类器的结果进行比较,统计随机森林分类器分类错误的数目,设为X,则袋外数据误差大小=X/O
优缺点 :
这已经经过证明是无偏估计的,所以在随机森林算法中不需要再进行交叉验证或者单独的测试集来获取测试集误差的无偏估计。
6. 随机森林的过拟合问题
- 你已经建了一个有10000棵树的随机森林模型。在得到0.00的训练误差后,你非常高兴。但是,验证错误是34.23。到底是怎么回事?你还没有训练好你的模型吗? 答:该模型过度拟合,因此,为了避免这些情况,我们要用交叉验证来调整树的数量。
7. 代码实现
0.import工具库
In [1]:
1 | import pandas as pd |
1.加载数据
In [2]:
1 | boston_house = load_boston() |
In [3]:
1 | boston_feature_name = boston_house.feature_names |
In [4]:
1 | boston_feature_name |
Out[4]:
1 | array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', |
构建模型
1 | help(RandomForestRegressor) |
1 | Help on class RandomForestRegressor in module sklearn.ensemble.forest: |
1 | rgs = RandomForestRegressor(n_estimators=15) ##随机森林模型 |
In [10]:
1 | rgs |
Out[10]:
1 | RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None, |
In [11]:
1 | rgs.predict(boston_features) |
Out[11]:
1 | array([ 26.16666667, 22.24 , 33.76666667, 33.67333333, |
1 | from sklearn import tree |
In [13]:
1 | rgs2 = tree.DecisionTreeRegressor() ##决策树模型,比较两个模型的预测结果! |
Out[13]:
1 | DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None, |
In [14]:
1 | rgs2.predict(boston_features) |
Out[14]:
1 | array([ 24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, |
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是Boosting的思想。
1. 解释一下GBDT算法的过程
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是Boosting的思想。
1.1 Boosting思想
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练
1.2 GBDT原来是这么回事
GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的残差(这个残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。
举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
- 它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
- 接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
- 接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
- 最后在第四课树中用1岁拟合剩下的残差,完美。
- 最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
为何gbdt可以用用负梯度近似残差呢?
回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
那此时的负梯度是这样计算的
所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 -
当前模型预测的值),即残差。此时的变量是,即“当前预测模型的值”,也就是对它求负梯度。
训练过程
简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点最多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图所示结果:
在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
- 此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
- 注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
- A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
- B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
- C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
- D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
2. 梯度提升和梯度下降的区别和联系是什么?
下表是梯度提升算法和梯度下降算法的对比情况。可以发现,两者都是在每 一轮迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更 新,
只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参 数的更新。
而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函 数空间中,从而大大扩展了可以使用的模型种类。
3. GBDT的优点和局限性有哪些?
3.1 优点
- 预测阶段的计算速度快,树与树之间可并行化计算。
- 在分布稠密的数据集上,泛化能力和表达能力都很好,这使得GBDT在Kaggle的众多竞赛中,经常名列榜首。
- 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系。
3.2 局限性
- GBDT在高维稀疏的数据集上,表现不如支持向量机或者神经网络。
- GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值特征时明显。
- 训练过程需要串行训练,只能在决策树内部采用一些局部并行的手段提高训练速度。
4. RF(随机森林)与GBDT之间的区别与联系
相同点 :
- 都是由多棵树组成,最终的结果都是由多棵树一起决定。
- RF和GBDT在使用CART树时,可以是分类树或者回归树。
不同点 :
- 组成随机森林的树可以并行生成,而GBDT是串行生成
- 随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之和
- 随机森林对异常值不敏感,而GBDT对异常值比较敏感
- 随机森林是减少模型的方差,而GBDT是减少模型的偏差
- 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化
5. 代码实现
GitHub:https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb
1 | import numpy as np |
获取训练数据
In [54]:
1 | train_feature = np.genfromtxt("train_feat.txt",dtype=np.float32) |
Out[54]:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.005988 | 0.569231 | 0.647059 | 0.951220 | -0.225434 | 0.837989 | 0.357258 | -0.003058 |
| 1 | 0.161677 | 0.743195 | 0.682353 | 0.960976 | -0.086705 | 0.780527 | 0.282945 | 0.149847 |
| 2 | 0.113772 | 0.744379 | 0.541176 | 0.990244 | -0.005780 | 0.721468 | 0.434110 | -0.318043 |
| 3 | 0.053892 | 0.608284 | 0.764706 | 0.951220 | -0.248555 | 0.821229 | 0.848604 | -0.003058 |
| 4 | 0.173653 | 0.866272 | 0.682353 | 0.951220 | 0.017341 | 0.704709 | -0.021002 | -0.195719 |
In [55]:
1 | train_label |
Out[55]:
1 | 0 320.0 |
获取测试数据
In [56]:
1 | test_feature = np.genfromtxt("test_feat.txt",dtype=np.float32) |
Out[56]:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.005988 | 0.569231 | 0.647059 | 0.951220 | -0.225434 | 0.837989 | 0.357258 | -0.003058 |
| 1 | 0.161677 | 0.743195 | 0.682353 | 0.960976 | -0.086705 | 0.780527 | 0.282945 | 0.149847 |
| 2 | 0.113772 | 0.744379 | 0.541176 | 0.990244 | -0.005780 | 0.721468 | 0.434110 | -0.318043 |
| 3 | 0.053892 | 0.608284 | 0.764706 | 0.951220 | -0.248555 | 0.821229 | 0.848604 | -0.003058 |
| 4 | 0.173653 | 0.866272 | 0.682353 | 0.951220 | 0.017341 | 0.704709 | -0.021002 | -0.195719 |
In [57]:
1 | test_label |
Out[57]:
1 | 0 320.0 |
GBDT模型建立
In [58]:
1 | gbdt = GradientBoostingRegressor( |
1 | pred: 320.0008173984891 label: 320.0 |
因果卷积
temporal convolutional network (TCN)
专为时间序列预测而设计的深度学习网络结构
参考https://zhuanlan.zhihu.com/p/422177151
动机


因果卷积神经网络的设计结构

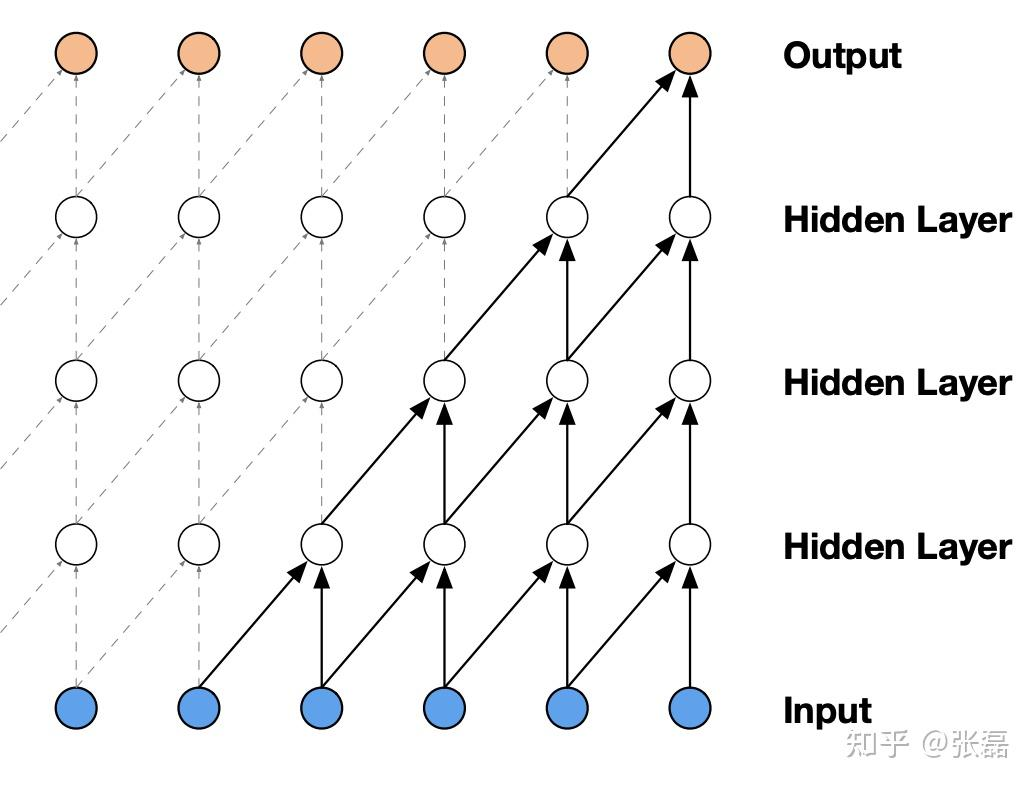
因果卷积神经网络 (causal convolutional network) 的基本结构
(缺陷)然而,当我们观察这样的网络结构时,也发现了一个问题:因果卷积对历史信息的覆盖范围不大,比如上面这个图中,最后的输出结果值能基于第一层输入中的5个神经元来计算,更前面的输入信息丢失浪费了。 (扩大因果卷积对历史数据的覆盖范围) 那么,怎么扩大因果卷积对历史数据的覆盖范围呢? 简单的一种思路是,我们可以不断增加网络深度,网络层数,即 layer 的数量越多,就可以逐渐扩大历史信息的捕捉视野,然而,这种方式显得有些差强人意,因为通过增加网络深度的方式只能在线性时间尺度上扩大对捕捉历史信息的捕捉,而且,随着深度的逐渐增大,网络中的参数也成倍增加,使得网络的训练难度迅速变大。 因此,这样的方式并非可取,那么有什么聪明的方法能够在网络不太深的情况下尽可能捕捉到尽可能多的信息历史呢?
为了解决这个问题,Oord et al. (2016)
提出了采用空洞卷积的方式来扩大因果卷积网络对历史信息的感受视野(reception
field)。
简单来说,就是在卷积核移动过程中加入了步长间隔dilation这个参数,比如在二维图像卷积中,传统的卷积是这样的:
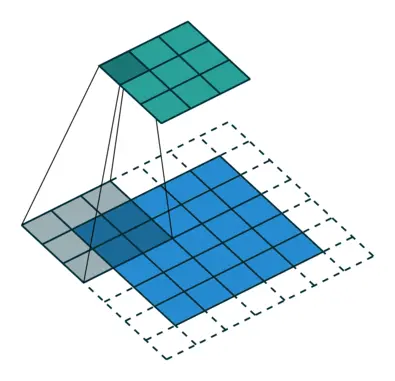
加入空洞卷积机制后的卷积: v2-c4c54d9b304259d1597b26c07c722a79_b
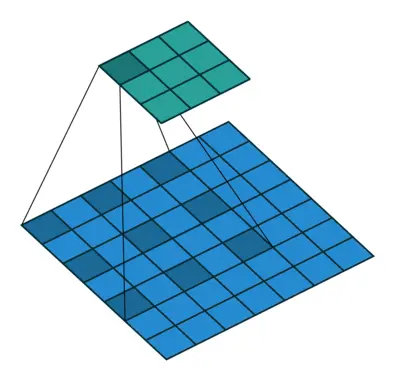
上面的两个动图的例子是针对二维形式的输入数据,那么简单的对于输入数据为一维向量时,加入dilation机制后的因果卷积神经网络结构图就是这样:
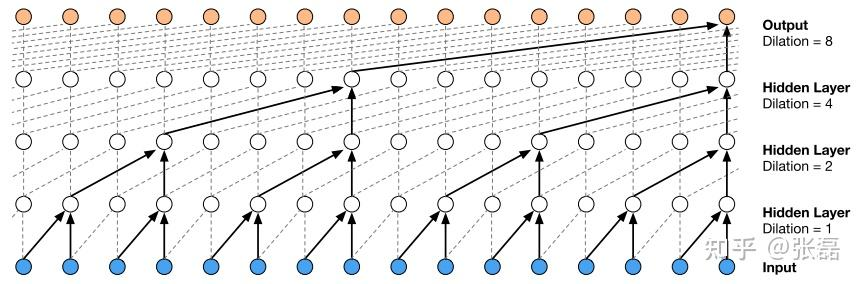

代码结合上面的图看:
1 | import numpy as np |

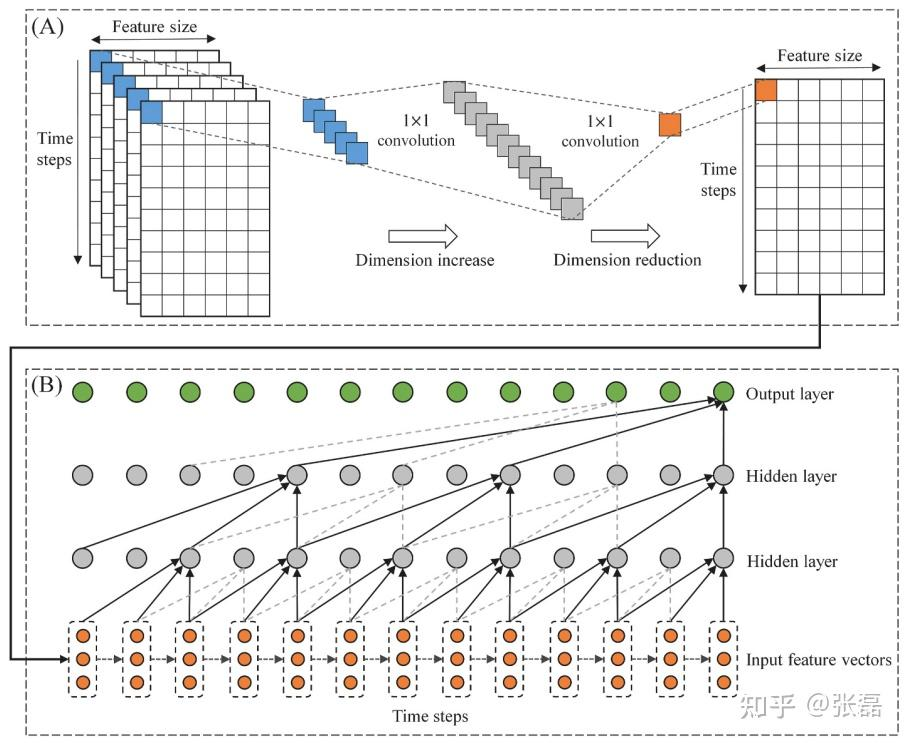
可以看到,由于空气污染PM2.5的数据是由空间上多个观测站点同时观测记录构成的,因此我们自然的想到当推测某一个站点区域内未来PM2.5浓度大小时,需要同时考虑其余站点与该目标站点之间存在的空间上的相关性,即多观测站点之间空间依赖。我们将这种空间依赖通过上图(A)部分中所示的 1 × 1 convolution 卷积算子进行处理,将多站点上对应时间和对应特征的数据值通过 1 × 1 卷积进行维度提升,再进行降维,从而将多站点的时间序列数据(3维)压缩到一个二维形式。然后在将此作为 CausalConvNet 的输入从而完成整个时空因果卷积网络的构建。
有关该研究的更多详细信息,欢迎阅读已发表在 Computers and Geosciences 上的论文:
论文信息:
Zhang, L., Na, J., Zhu, J., Shi, Z., Zou, C., Yang, L., 2021. Spatiotemporal causal convolutional network for forecasting hourly PM2.5 concentrations in Beijing, China. Computers & Geosciences 155, 104869. DOI: https://doi.org/10.1016/j.cageo.2021.104869
weight_norm权重归一化
注意:
weight_norm是PyTorch中的一种权重归一化方法,还有其他归一化方法如Batch Normalization等。- 根据具体任务和模型结构选择合适的归一化方法。
定义第一个卷积层,并使用weight_norm函数对卷积层的权重进行归一化。
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))权重归一化(Weight Normalization)是一种在深度学习中常用的技术,主要用于加速模型的训练过程,提高模型的稳定性,并有助于防止梯度消失或爆炸。以下是一些常见的场景,在这些场景中,对权重进行归一化可能特别有用:
训练深层神经网络:
- 深层神经网络(如ResNet、VGG等)通常包含大量的权重参数,这些参数的初始化和更新对模型的训练效果有很大影响。权重归一化可以稳定这些参数的更新过程,加速收敛。
处理梯度消失或爆炸问题:
- 在深层神经网络中,梯度消失和梯度爆炸是常见的问题。权重归一化通过调整权重的大小,可以减少这些问题的出现,从而提高模型的训练稳定性。
加速训练过程:
- 权重归一化可以加速模型的训练过程。通过稳定权重参数的更新,模型可以更快地收敛到最优解。
提高模型泛化能力:
- 权重归一化有助于模型更好地泛化到新的数据集。通过减少权重参数的方差,模型可以更好地捕捉到数据的全局特征,从而提高泛化能力。
处理时间序列数据:
- 在处理时间序列数据时,一维卷积层(如 \(nn.Conv1d\))经常被使用。权重归一化可以稳定这些卷积层的权重更新,提高模型对时间序列数据的处理能力。
处理语音信号:
- 在语音信号处理任务中,一维卷积层也经常被使用。权重归一化可以稳定这些卷积层的权重更新,提高模型对语音信号的处理能力。
处理图像数据:
- 在图像处理任务中,虽然通常使用二维卷积层(如
nn.Conv2d),但权重归一化也可以应用于这些层,以提高模型的训练效率和稳定性。
- 在图像处理任务中,虽然通常使用二维卷积层(如
注意事项
计算复杂度:
- 权重归一化会增加模型的计算复杂度,因为需要额外的计算步骤来归一化权重。
参数调整:
- 权重归一化需要调整一些参数,如归一化因子等,这些参数的选择可能会影响模型的性能。
与其他正则化技术的结合:
- 权重归一化可以与其他正则化技术(如dropout、L2正则化等)结合使用,以进一步提高模型的泛化能力和训练稳定性。
总之,权重归一化是一种非常有用的技术,可以在多种场景下提高模型的训练效率和稳定性。然而,也需要根据具体任务和模型结构选择合适的归一化方法,并进行适当的参数调整。
除了
weight_norm,还有其他几种常见的权重归一化方法,包括:
https://blog.csdn.net/wxc971231/article/details/139925707
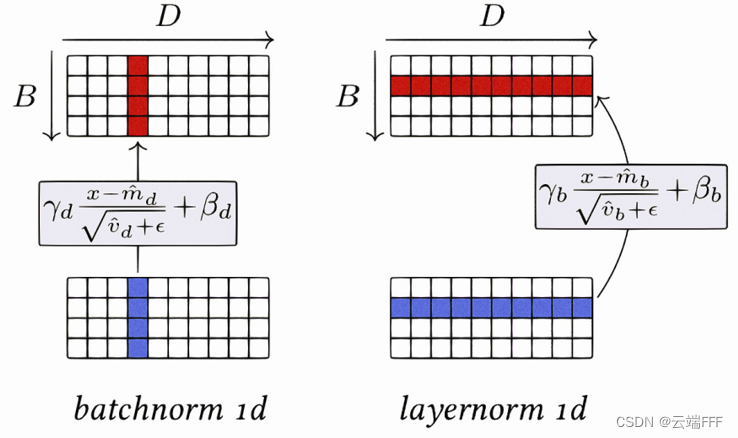
Batch Normalization(批归一化):
- Batch Normalization是一种在训练深层神经网络时常用的技术,它通过对每个小批量数据的激活值进行归一化,这消除了不同特征之间的大小关系,但是保留了不同样本间的大小关系,使得网络更容易训练。Batch Normalization不仅可以加速模型的训练过程,还可以提高模型的泛化能力。BatchNorm 适用于 CV 领域,这时输入尺寸为 b × c × h × w (批量大小x通道x长x宽),图像的每个通道 c 看作一个特征,BN 可以把各通道特征图的数量级调整到差不多,同时保持不同图片相同通道特征图间的相对大小关系

BatchNorm是一种在深度学习训练中广泛使用的归一化技术,有很多好处,包括正则化效应、减少过拟合、减少对权重初始值的依赖、允许使用更高的学习率等
一方面,BN 使每一层隐藏值分布主动居中,并将它们重新调整为学习到的最佳均值和方差,这种操作可能将参数的量级进行了统一,因此直觉上往往被认为可以使优化更加平滑 (科学性存在争议)另一方面,BN 有效性的科学性解释一度存在争议。15 年提出BN的论文(https://papers.cool/arxiv/1502.03167)声称 BN 减小了所谓的 内部协变量偏移internal covariate shift,因此可以提高模型性能,但其分析中假设了每层隐变量值都服从某种正态分布,这个假设过强了,很多后续研究指出了其问题。18 年的论文 《How Does Batch Normalization Help Optimization?》认为 BN 的主要作用是使得整个损失函数的 landscape 更为平滑,从而使得我们可以更平稳地进行训练。相关分析可以参考苏神的博文(https://kexue.fm/archives/6992) 注意:后面其他节也有关于 Lispschitz 的一些理解补充,需要结合一起看(https://zhuanlan.zhihu.com/p/520107941):
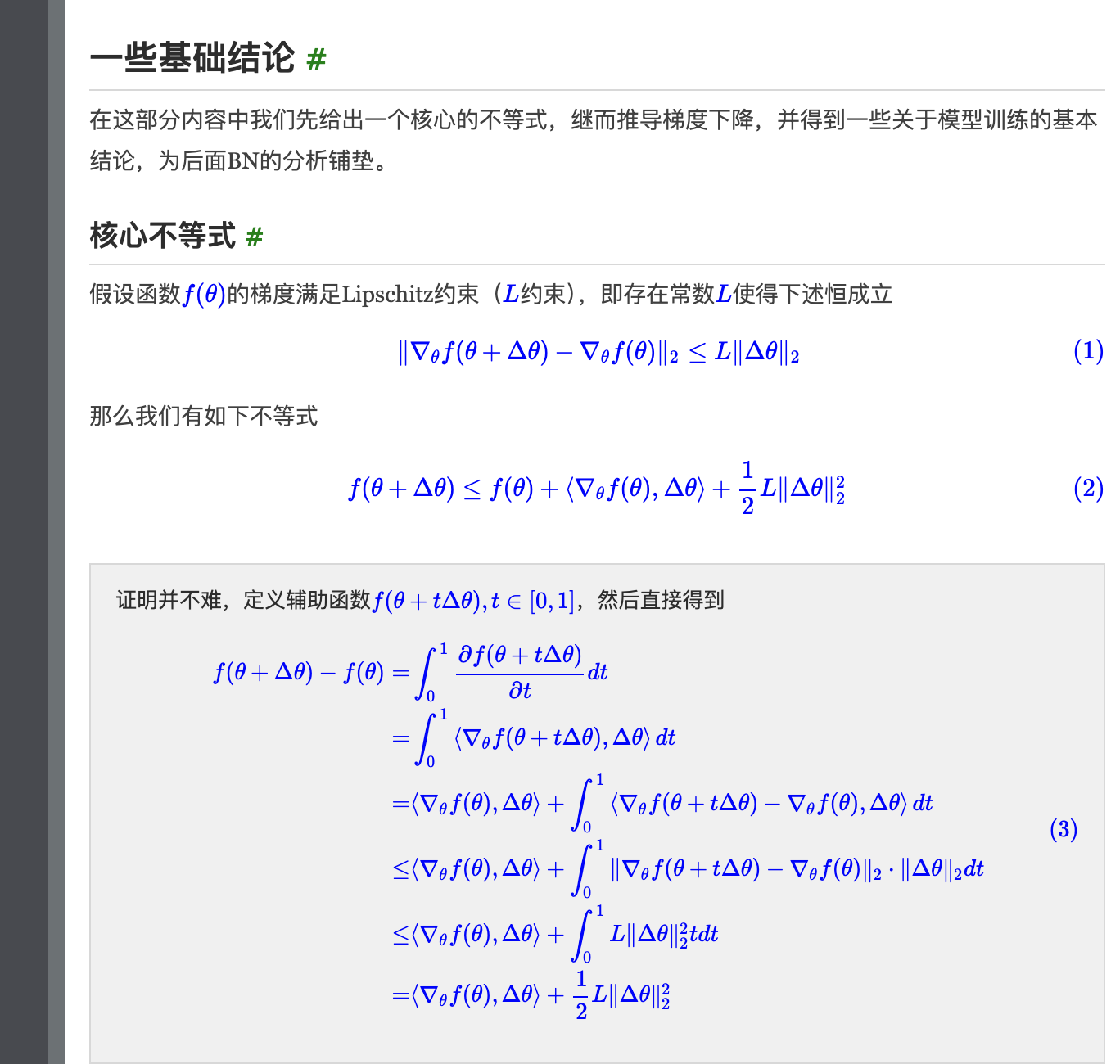

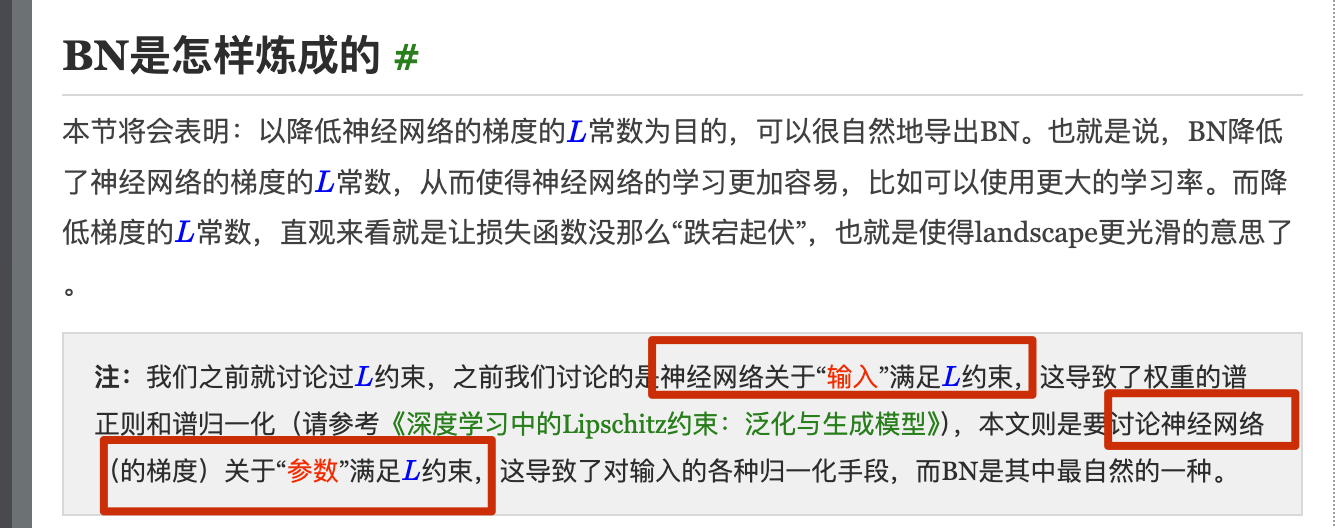 即下面的:
即下面的:
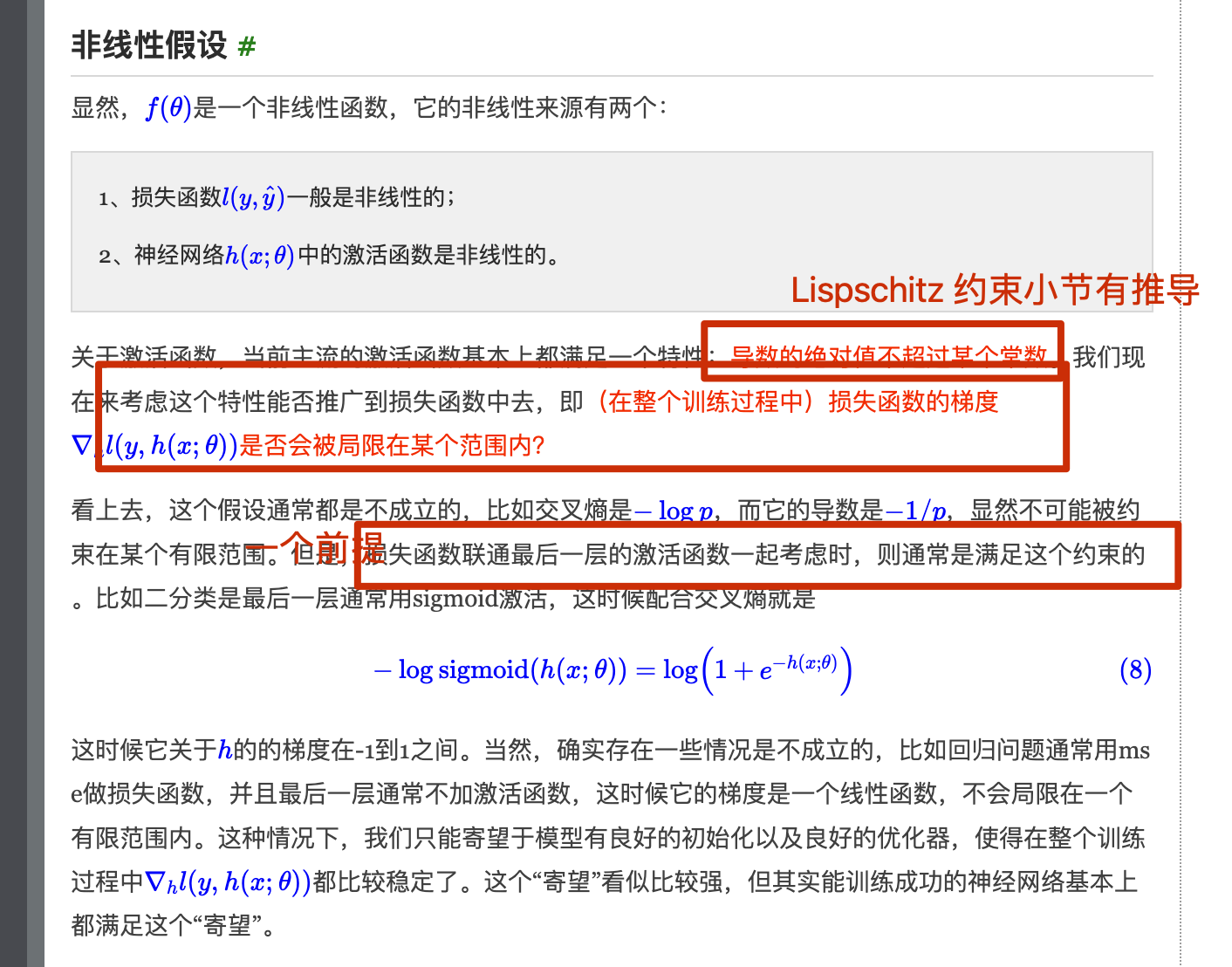



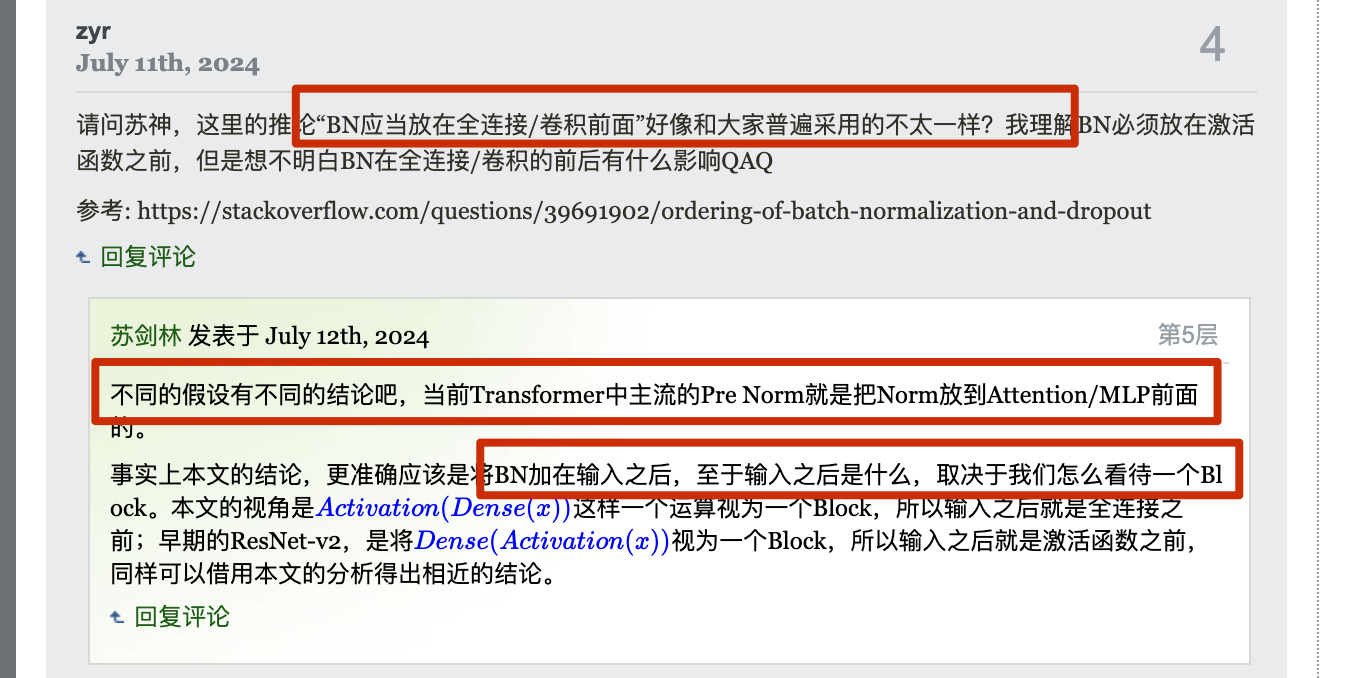
1 | class BatchNorm(nn.Module): |
Layer Normalization(层归一化):
- Layer Normalization与Batch Normalization类似,但它是在整个输入层上进行的归一化操作,而不是在每个小批量数据上(对每个样本的所有特征做归一化,这消除了不同样本间的大小关系,但是保留了一个样本内不同特征之间的大小关系)。Layer Normalization适用于序列模型,如RNN和Transformer。LayerNorm 适用于 NLP 领域,这时输入尺寸为 b × l × d (批量大小x序列长度x嵌入维度),如下图所示
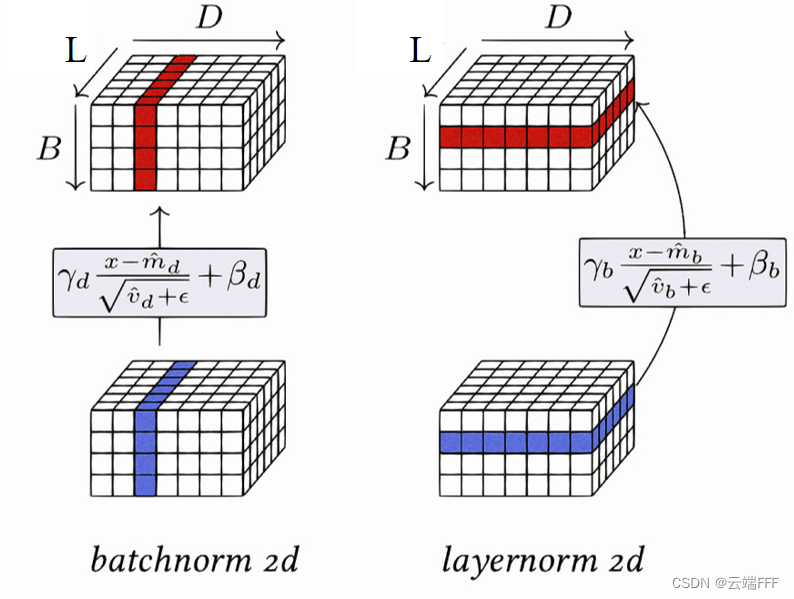
- 注意这时长 l ll 的 token 序列中,每个 token 对应一个长为 d 的特征向量,LayerNorm 会对各个 token 执行 l 次归一化计算,保留每个 token d 维嵌入内部的相对大小关系,同时拉近了不同 token 对应特征向量间的距离。与之相比,BN 会消除 d 维特征向量各维度之间的大小关系,破坏了 token 的特征(以下第 2 节会进一步说明这一点)

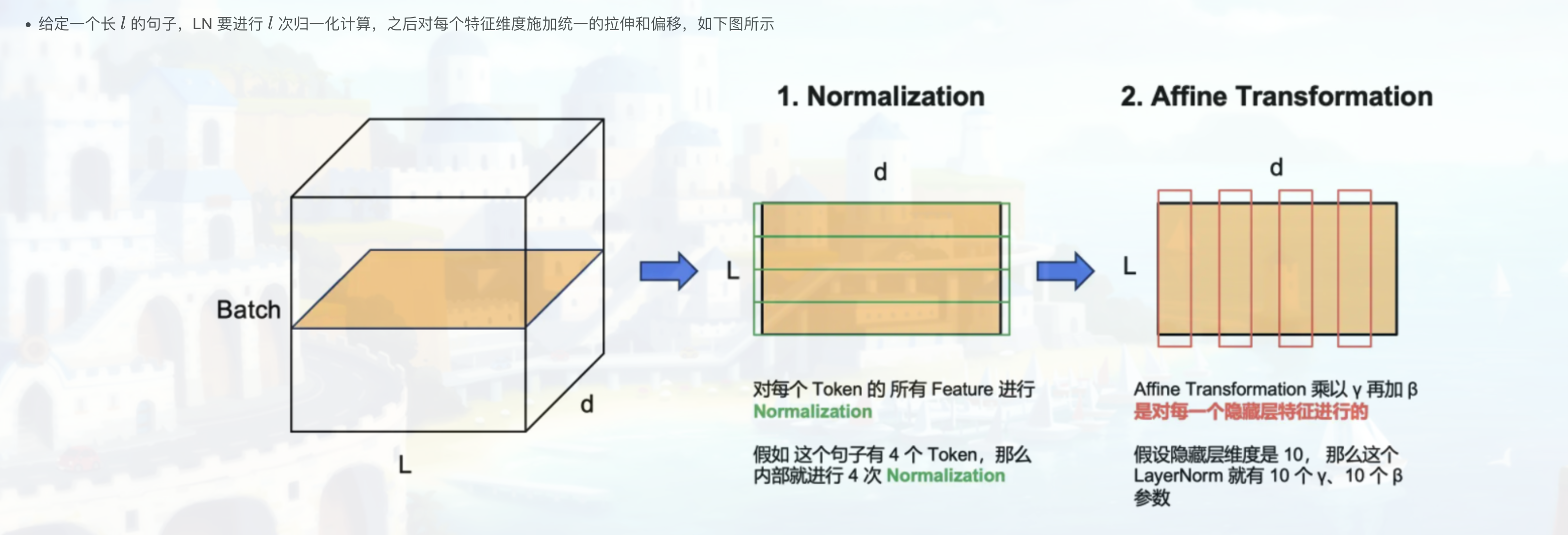

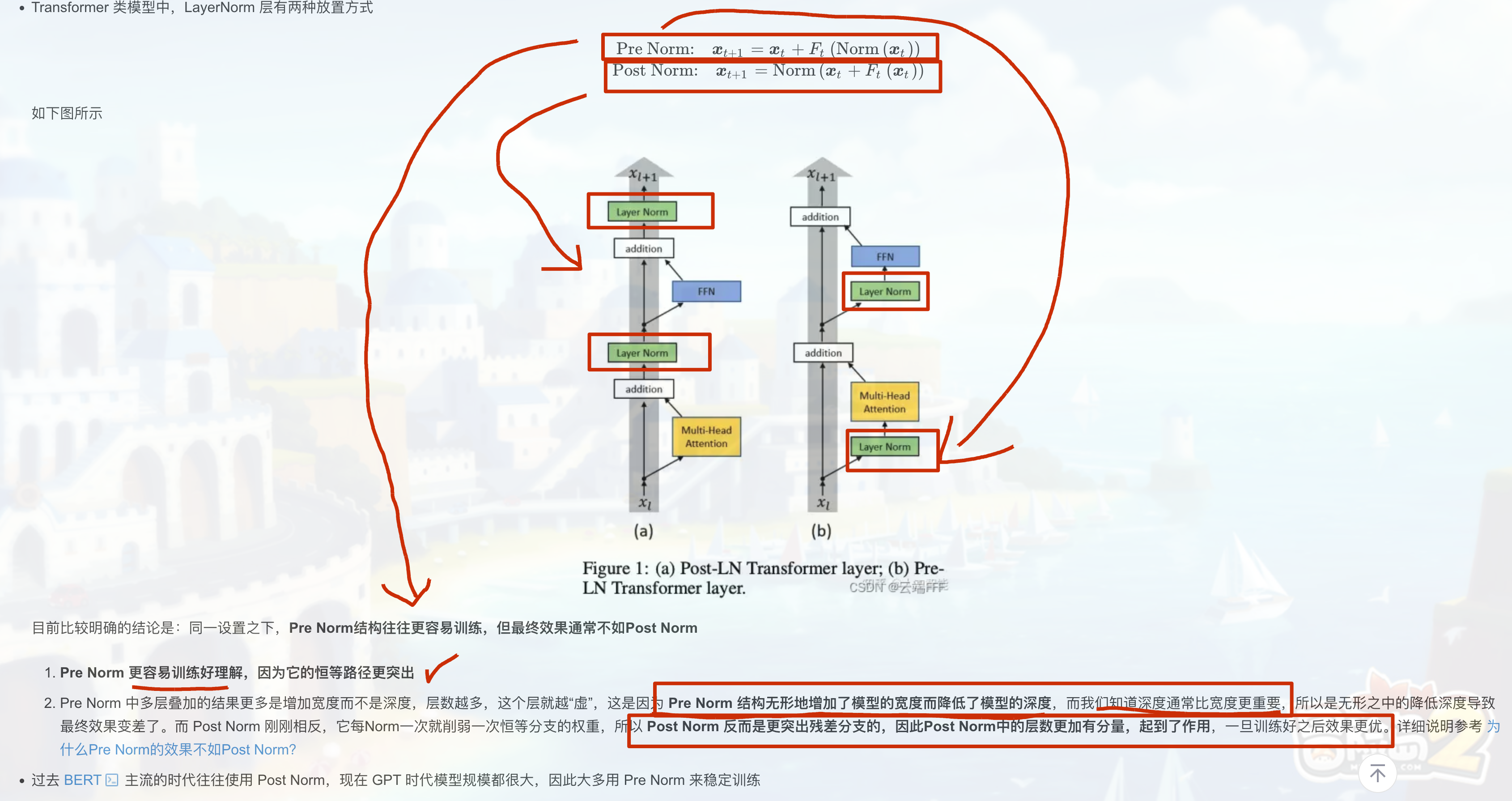
为什么Pre Norm的效果不如Post Norm? https://kexue.fm/archives/9009

什么是 warmup?


不理解

首先,“同一量级” 应该是指每次经过 Norm 和 F 函数处理后,输出的向量模长或各分量的大小保持在相似的范围,比如经过 Layer Normalization 后,数据的均值和方差被标准化,所以每次 F 的输出不会有太大的数值变化。假设每一项 Fₜ(Norm (xₜ)) 的模长大约为常数 C,那么累加 t+1 项后,xₜ₊₁的模长大约是 (t+1)*C,也就是 O (t+1)。
接下来,第 t+1 层和第 t 层的差别是 Fₜ(Norm (xₜ)),其模长是 C,而 xₜ的模长是 tC,所以相对差别是 C/(tC)=1/t,当 t 很大时,这个相对差别趋近于 0,意味着相邻层之间的变化越来越小,模型的有效深度被稀释,因为每层的贡献相对于总输出来说变得微不足道,导致深层的信息更新不明显,相当于模型实际深度没有层数显示的那么深,而是更像宽度的增加,因为每层的贡献相似,堆叠起来更像增加了宽度而不是深度。 https://www.zhihu.com/question/519668254/answer/2371885202 On Layer Normalization in Transformer Architecture
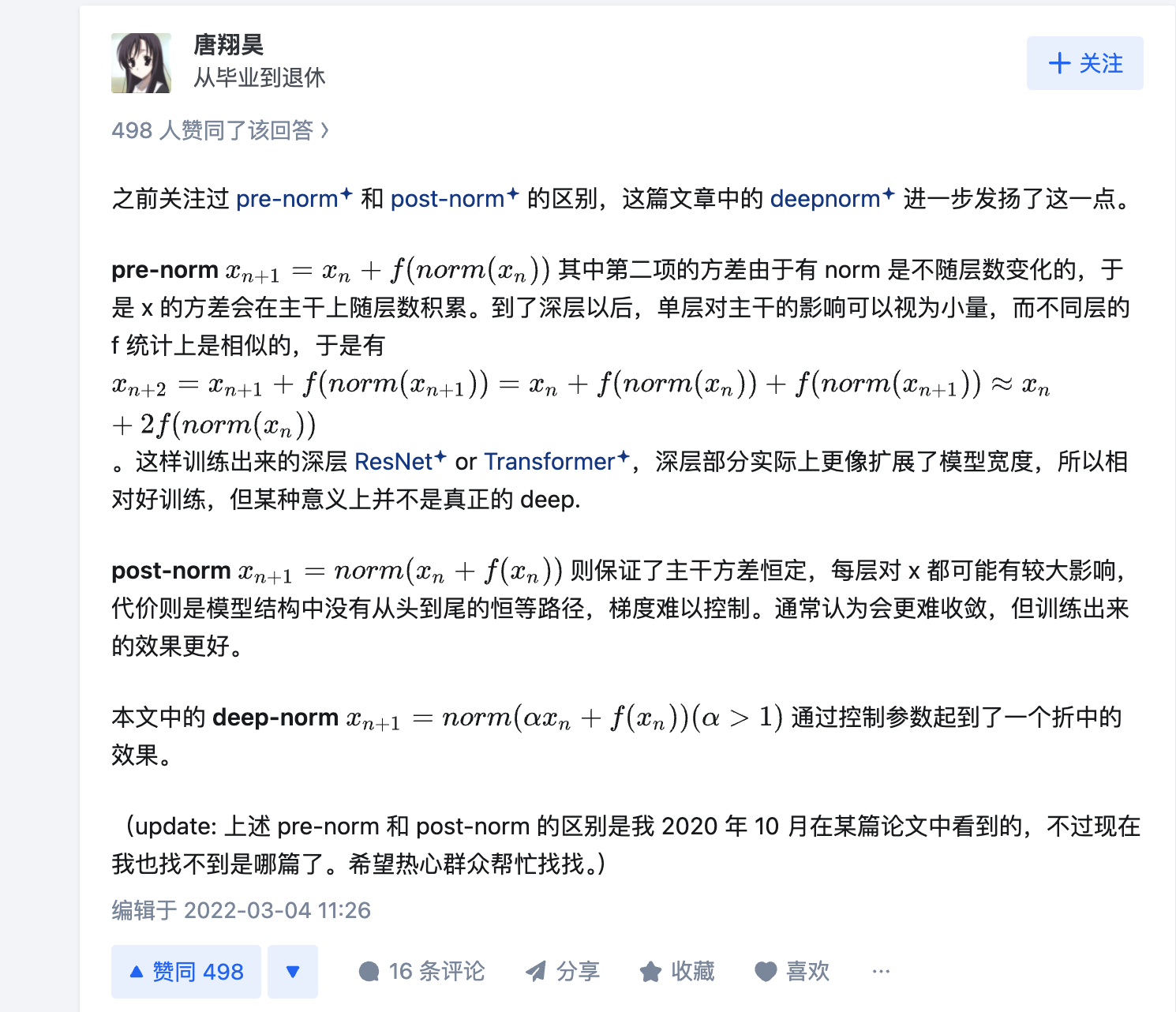
rmsNorm 
1 | class LlamaRMSNorm(nn.Module): |
Instance Normalization(实例归一化):
- Instance Normalization是在每个样本的每个通道上进行的归一化操作,而不是在整个批次或整个层上。Instance Normalization常用于图像生成模型,如GAN和StyleGAN。
Group Normalization(组归一化):
- Group Normalization是一种介于Batch Normalization和Layer Normalization之间的归一化方法。它将输入的通道分成若干组,然后在每个组内进行归一化操作。Group Normalization可以在一定程度上缓解Batch Normalization在训练小批量数据时的不稳定问题。
Layer-wise Scale and Bias(层归一化):
- 这种方法是在每个神经元的输出上添加可学习的缩放和偏移参数,以实现归一化效果。这种方法类似于Batch Normalization,但它是在每个神经元上独立进行的,而不是在整个层或整个批次上。
Group-wise Factorization(组归一化):
- 这种方法将卷积层的权重分解为两个矩阵,然后对这两个矩阵分别进行归一化操作。这种方法可以在一定程度上提高模型的训练效率和泛化能力。
这些归一化方法各有优缺点,选择哪种方法取决于具体任务和模型结构。在实际应用中,通常需要根据实验结果来选择最合适的归一化方法。 归一化是常用的稳定训练的手段,CV 中常用 Batch Norm; Transformer 类模型中常用 layer norm,而 RMSNorm 是近期很流行的 LaMMa 模型使用的标准化方法,它是 Layer Norm 的一个变体
从一维卷积、因果卷积(Causal CNN)、扩展卷积(Dilation CNN) 到 时间卷积网络 (TCN)
引言
卷积神经网络 (CNN) 尽管通常与图像分类任务相关,但经过改造,同样可以用于序列建模预测。在本文中,我们将详细探讨时间卷积网络 (TCN) 所包含的基本构建块,以及它们如何组合在一起从而变成强大的预测模型。本文对 时间卷积网络 (TCN) 的描述基于以下论文:https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1803.01271.pdf
背景介绍
直到最近,深度学习背景下的序列建模主题在很大程度上与循环神经网络架构有关,例如 LSTM 和 GRU。 S. Bai等人表明这种思维方式已经过时,在对序列数据进行建模时,应将卷积网络作为主要候选者之一。 他们证明了卷积网络可以在许多任务中实现比 RNN 更好的性能,同时避免循环模型的常见缺点,例如梯度爆炸/消失问题或缺乏记忆保留 。 此外,使用卷积网络可以提高性能,因为它允许并行计算输出。 他们提出的架构称为时间卷积网络 (TCN),将在以下部分中进行解释。
卷积模型
TCN是时域卷积网络的缩写,由具有相同输入和输出长度的扩展(dilated)/因果(causal)一维卷积层组成。下面将详细介绍这些术语的实际含义。
一维卷积网络
一维卷积网络将一个 3 维张量作为输入,并输出一个 3 维张量。我们的 TCN 实现的输入张量具有形状 (batch_size, input_length, input_size),输出张量具有形状 (batch_size, input_length, output_size)。 由于 TCN 中的每一层都具有相同的输入和输出长度,因此只有输入和输出张量的第三维不同。 在单变量情况下,input_size 和 output_size 都将等于 1。 在更一般的多变量情况下,input_size 和 output_size 可能不同,因为我们可能不想预测输入序列的每个分量。
一个单一的 1D 卷积层接收一个形状为 (batch_size, input_length, nr_input_channels) 的输入张量,并输出一个形状为 (batch_size, input_length, nr_output_channels) 的张量。 要了解单个层如何将其输入转换为输出,让我们看一下批处理中的一个元素(批处理中的每个元素都发生相同的过程)。 让我们从最简单的情况开始,其中 nr_input_channels 和 nr_output_channels 都等于 1。在这种情况下,我们正在查看 1D 输入和输出张量。下图显示了如何计算输出张量的一个元素。
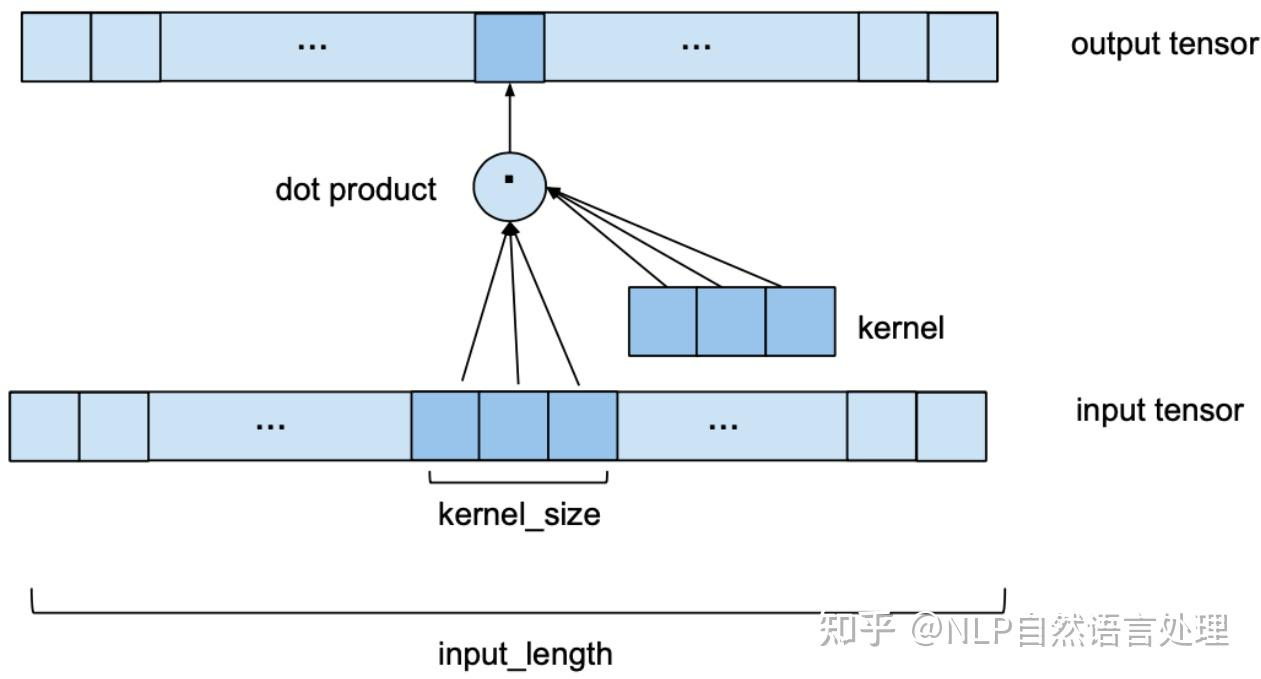
可以看到,为了计算输出的一个元素,我们查看输入的长度为 kernel_size 的一系列连续元素。 在上面的示例中,我们选择了 kernel_size 为 3。 为了获得输出,我们将输入的子序列与相同长度的学习权重的核向量进行点积。 为了获得输出的下一个元素,应用相同的过程,但是输入序列的 kernel_size 大小的窗口向右移动一个元素(对于这个预测模型,步幅始终设置为 1)。这里需要注意,同一组内核权重将用于计算一个卷积层的每个输出。 下图显示了两个连续的输出元素及其各自的输入子序列。
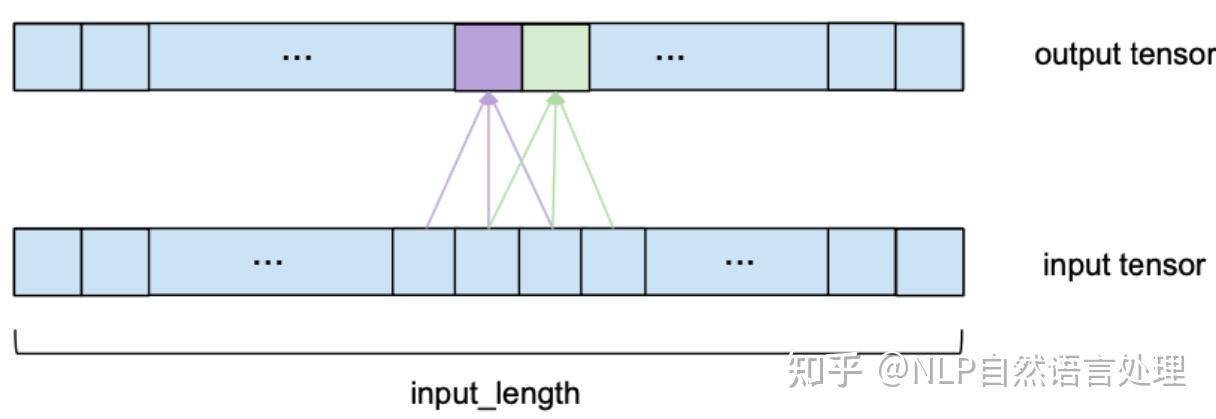
为了使可视化更简单,不再显示具有核向量的点积,而是针对具有相同核权重的每个输出元素进行。
为了确保输出序列与输入序列具有相同的长度,应用了一些零填充。这意味着将额外的零值条目添加到输入张量的开头或结尾,以确保输出具有所需的长度。具体如何做到这一点将在后面解释。
现在让我们看看我们有多个输入通道的情况,即 nr_input_channels 大于 1。在这种情况下,上述过程对每个输入通道重复,但每次使用不同的内核。这将生成 nr_input_channels 中间输出向量和一些 kernel_size * nr_input_channels 的内核权重。然后,将所有的中间输出向量相加得到最终的输出向量。从某种意义上说,这相当于一个二维卷积,其输入张量为 (input_size, nr_input_channels),内核为 (kernel_size, nr_input_channels),如下图所示。它仍然是 1D,因为窗口仅沿单个轴移动,但我们在每一步都有一个 2D 卷积,因为我们使用的是 2 维内核矩阵。
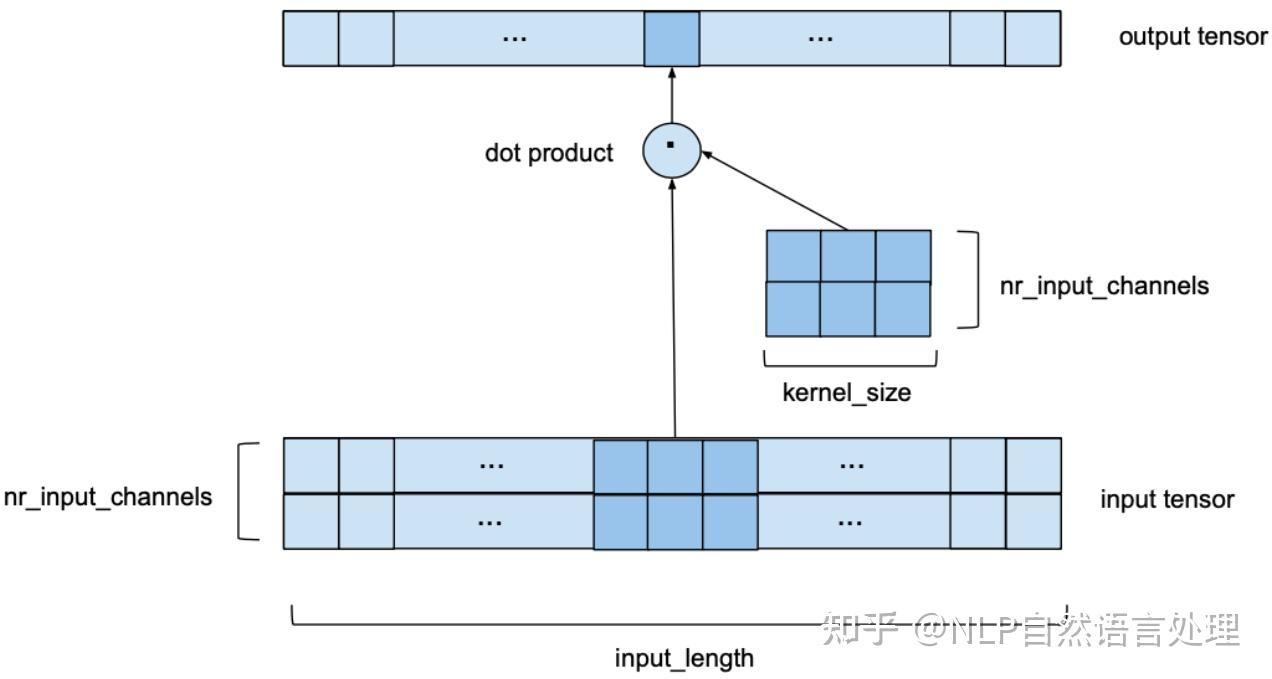
对于这个例子,我们选择 nr_input_channels 等于 2。现在,我们有一个 nr_input_channels 通过 kernel_size 内核矩阵沿 nr_input_channels 宽系列长度 input_length 滑动,而不是在 1 维输入序列上滑动。
如果 nr_input_channels 和 nr_output_channels 都大于 1,则只需对具有不同内核矩阵的每个输出通道重复上述过程。 然后将输出向量堆叠在一起,形成形状为 (input_length, nr_output_channels) 的输出张量。 在这种情况下,内核权重的数量等于 kernel_sizenr_input_channelsnr_output_channels。
两个变量 nr_input_channels 和 nr_output_channels 取决于层在网络中的位置。 第一层的 nr_input_channels = input_size,最后一层的 nr_output_channels = output_size。 所有其他层将使用 num_filters 给出的中间通道号。
因果(Causal )卷积
对于因果关系的卷积层,对于\(\{0,...,input\_length—1\}\) 中的每个i,输出序列的第i个元素可能仅取决于索引为 {0, ..., i} 的输入序列的元素。换句话说,输出序列中的一个元素只能依赖于输入序列中它之前的元素。 如前所述,为了确保输出张量与输入张量具有相同的长度,我们需要应用零填充。 如果我们只在输入张量的左侧应用零填充,那么将确保因果卷积。要理解这一点,请考虑最右边的输出元素。鉴于输入序列的右侧没有填充,它依赖的最后一个元素是输入的最后一个元素。现在考虑输出序列的倒数第二个输出元素。与最后一个输出元素相比,它的内核窗口向左移动了一个,这意味着它在输入序列中最右边的依赖关系是输入序列的倒数第二个元素。通过归纳可知,对于输出序列中的每个元素,其在输入序列中的最新依赖项具有与其自身相同的索引。 下图显示了 input_length 为 4 且 kernel_size 为 3 的示例。
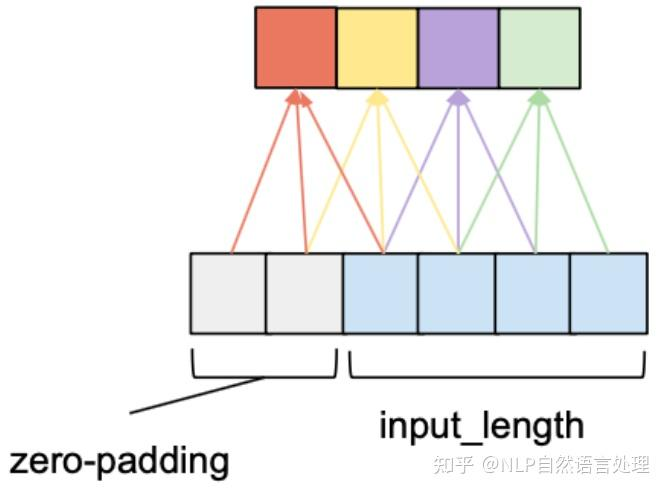
我们可以看到,通过 2 个条目的左零填充,我们可以在遵守因果关系规则的同时实现相同的输出长度。 事实上,在没有膨胀的情况下,维持输入长度所需的零填充条目数始终等于 kernel_size – 1。
扩张(Dilation)卷积
预测模型的一个理想特性是,输出中特定条目的值依赖于输入中所有之前的条目,即索引小于或等于其本身的所有条目。 当接收字段(即影响输出的特定条目的原始输入条目集)的大小为input_length时,就可以实现这一点。我们也称之为“全历史报道”。正如我们前面看到的,一个传统的卷积层使输出中的条目依赖于索引小于或等于其本身的输入的kernel_size条目。例如,如果kernel_size为3,则输出中的第5个元素将依赖于输入的元素3,4和5。 当我们 「把多层叠在一起时,这个范围就会扩大。在下面的图中,我们可以看到通过使用kernel_size 3堆叠两个层,我们得到了一个大小为5的接收字段」 。
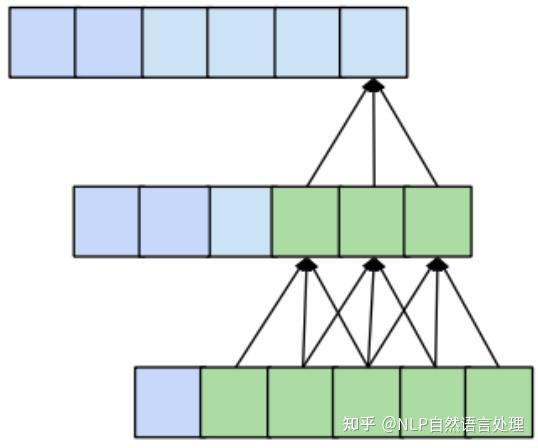
更一般地,具有 n 层和 kernel_sizek 的一维卷积网络具有大小为r的感受区域。[Math Processing Error] 要知道全覆盖需要多少层,我们可以将感受野大小设置为 input_length l 并求解层数 n(如果是非整数值,我们需要四舍五入):[Math Processing Error]n=[(l−1)/(k−1)] 这意味着,给定一个固定的 kernel_size,完整覆盖所需的层数与输入张量的长度呈线性关系,这将导致网络变得非常深非常快,从而导致模型具有非常多的参数 需要更长的时间来训练。 此外,随着模型层数越多其梯度消失的问题也就很容易出现。 「在保持层数相对较小的同时增加感受区域大小的一种方法是将膨胀引入卷积网络」 。
卷积层上下文中的扩展是指输入序列的元素之间的距离,这些元素用于计算输出序列的一个条目。 因此,传统的卷积层可以看作是 1-dilated 层,因为 1 个输出值的输入元素是相邻的。 下图显示了一个 2-dilated 层的示例,其中 input_length 为 4,kernel_size 为 3。
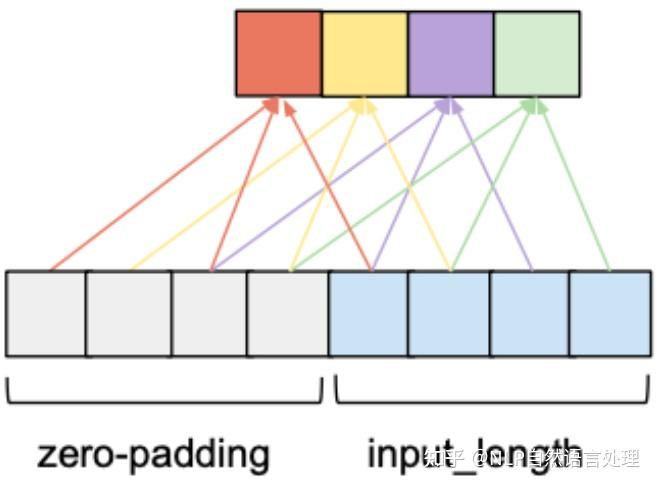
与 1-dilated 的情况相比,该层的感受区域分布在 5 而不是 3 的长度上。更一般地,内核大小为 k 的 d-dilated 层的感受野分布在 1+d∗(k−1) 的长度上。 如果 d 是固定的,这仍然需要一个与输入张量长度呈线性关系的数字来实现完全的感受野覆盖。
这个问题可以通过随着我们向上移动层而以指数方式增加 d 的值来解决。 为此,我们选择一个常数 dilation_base 整数 b,它将让我们计算特定层的扩张 d 作为其下方层数 i 的函数,如 d=bi。 下图显示了一个 input_length 为 10、kernel_size 为 3 和 dilation_base 为 2 的网络,它产生了 3 个扩张卷积层以实现全覆盖。
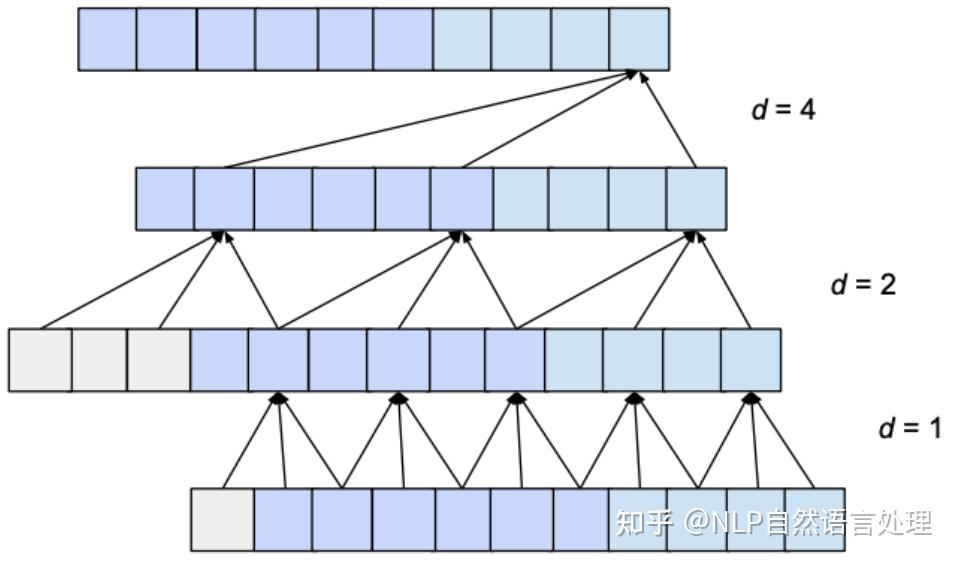
在这里,我们只展示了输入对最后一个输出值的影响。 同样,仅显示最后一个输出值所需的零填充条目。 显然,最后一个输出值取决于整个输入覆盖范围。 实际上,给定超参数,可以使用高达 15 的 input_length,同时保持完整的感受野覆盖。 一般来说,每个额外的层都会在当前感受野宽度上增加一个 \(d∗(k−1)\) 的值,其中 d 计算为 \(d=b^i\),i 表示新层之下的层数。 因此,具有基 b 指数膨胀、内核大小 k 和层数 n 的 TCN 的感受区域 w 的宽度由下式可以计算得出:
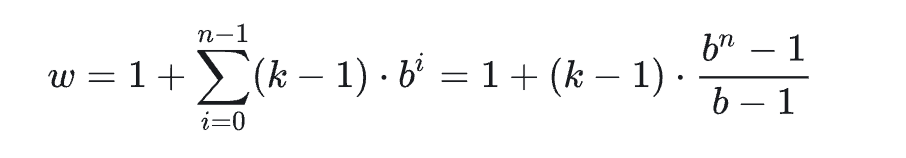
然而,根据 b 和 k 的值,这个感受野可能有“洞”。 考虑以下具有 3 的 dilation_base 和 2 的内核大小的网络:
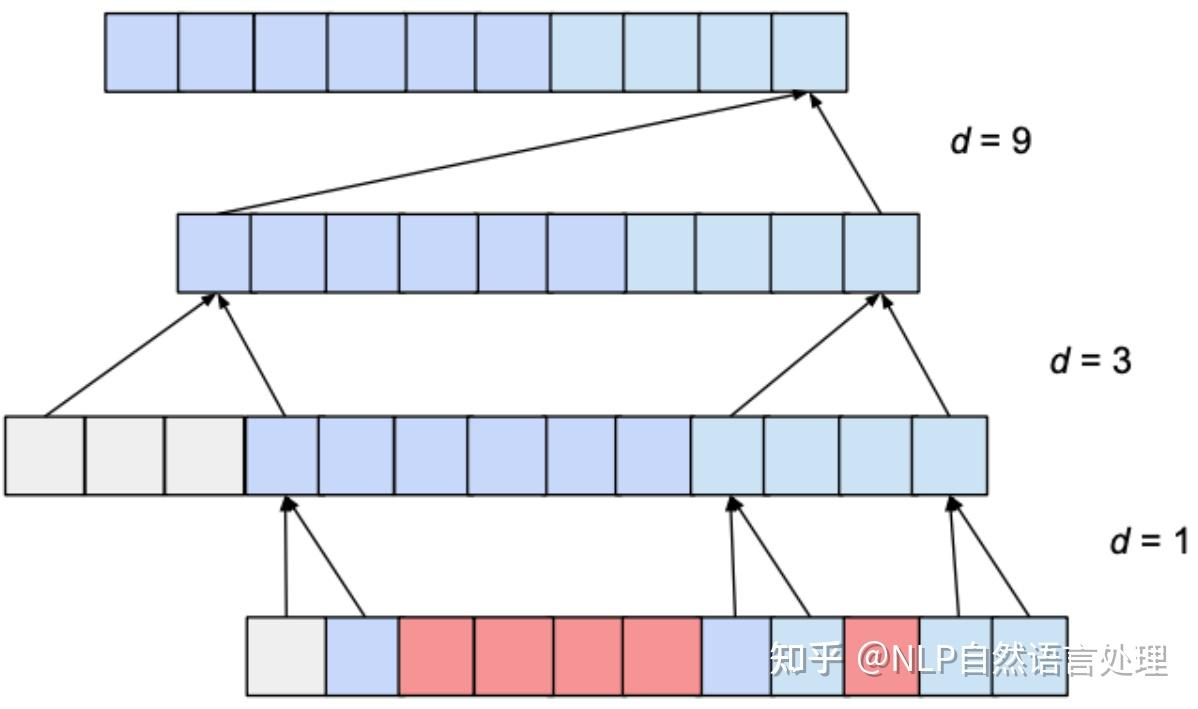
感受区域域覆盖的范围确实大于输入大小(即15)。然而,大脑的接受野上有洞;也就是说,在输入序列中有输出值不依赖的条目(如上红色部分所示)。 「要解决‘漏洞’这个问题,我们需要将内核大小增加到3,或者将膨胀基数减少到2」 。一般来说,对于一个没有孔的接受区域,核的大小k必须至少与膨胀底b一样大。
考虑到这些观察结果,可以计算出我们的网络需要多少层才能覆盖完整的历史记录。假设核大小为k,膨胀基数为b,其中k≥b,输入长度为l,对于全历史覆盖必须满足以下不等式:
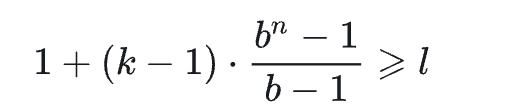
我们可以求解 n 并获得所需的最小层数为:
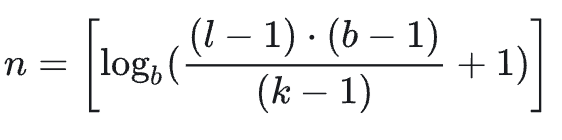
我们可以看到,层数现在在输入长度上是对数的,而不是线性的。 这是一个显着的改进,可以在不牺牲感受野覆盖范围的情况下实现。
现在唯一需要指定的是每层所需的零填充条目的数量。 给定一个扩张基数 b、一个内核大小 k 和当前层以下的 i 层数,则当前层所需的零填充条目数 p 计算如下:
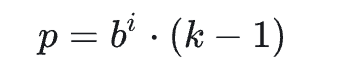
基础TCN模型
给定 input_length、kernel_size、dilation_base 和完整历史覆盖所需的最小层数,基本的 TCN 网络看起来像这样:
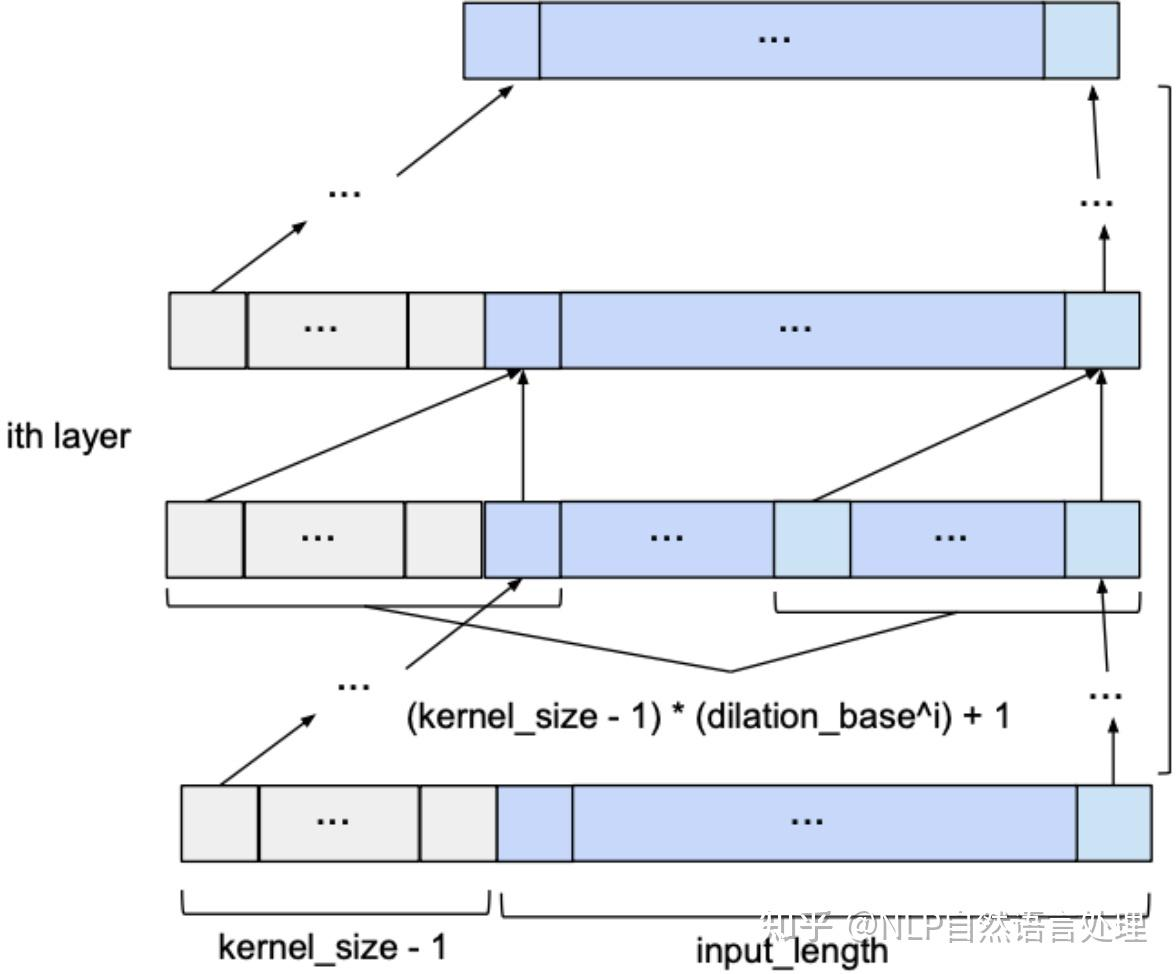
预测(Forecasting)
到目前为止,我们只讨论了“输入序列”和“输出序列”,而没有讨论它们之间的关系。在上下文预测中,我们希望预测未来时间序列的下一个条目。 为了训练我们的 TCN 网络进行预测,训练集将由(输入序列,目标序列)--给定时间序列的大小相等的子序列对组成。 目标序列将是相对于其各自的输入序列向前移动output_length步幅的序列。 这意味着长度为input_length的目标序列包含其各自输入序列的最后一个(input_length - output_length)元素作为第一个元素,而位于输入序列最后一个条目之后的output_length元素作为最后一个元素。 在上下文预测中,这意味着用这种模型可以预测的最大预测范围等于output_length。 使用滑动窗口方法,可以从一个时间序列中创建许多重叠的输入和目标序列对。
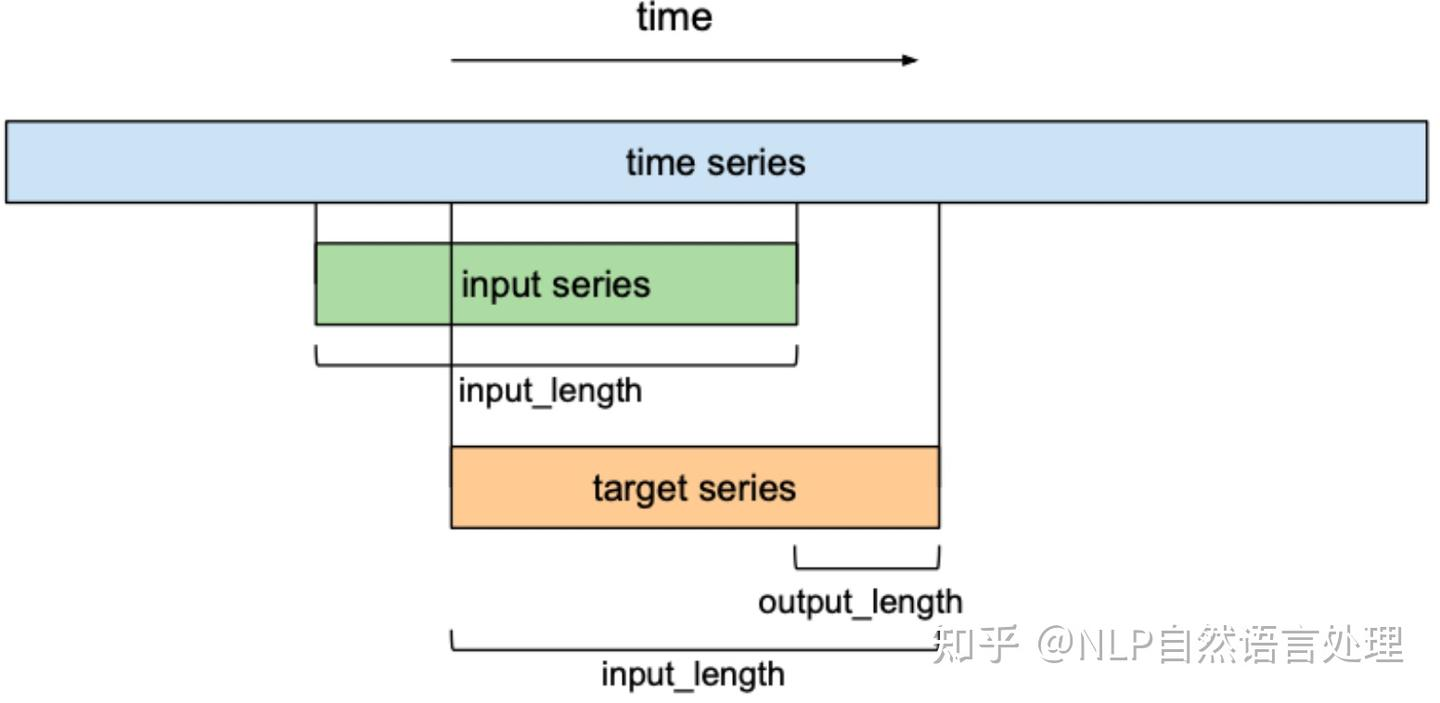
TCN模型升级
S. Bai提出对基本 TCN 架构进行一些添加(即残差连接、正则化和激活函数)以提高其性能。以下对时间卷积网络的描述基于以下论文
https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1803.01271.pdf
残差块
之前介绍的基本TCN模型所做的最大修改是将模型的基本构建块从简单的一维因果卷积层更改为由具有相同扩张因子和残差连接的2层残差块。
让我们考虑一个来自基本模型的膨胀因子 d 为 2 和内核大小 k 为 3 的层,看看它如何转化为改进模型的残差块。首先如下图:
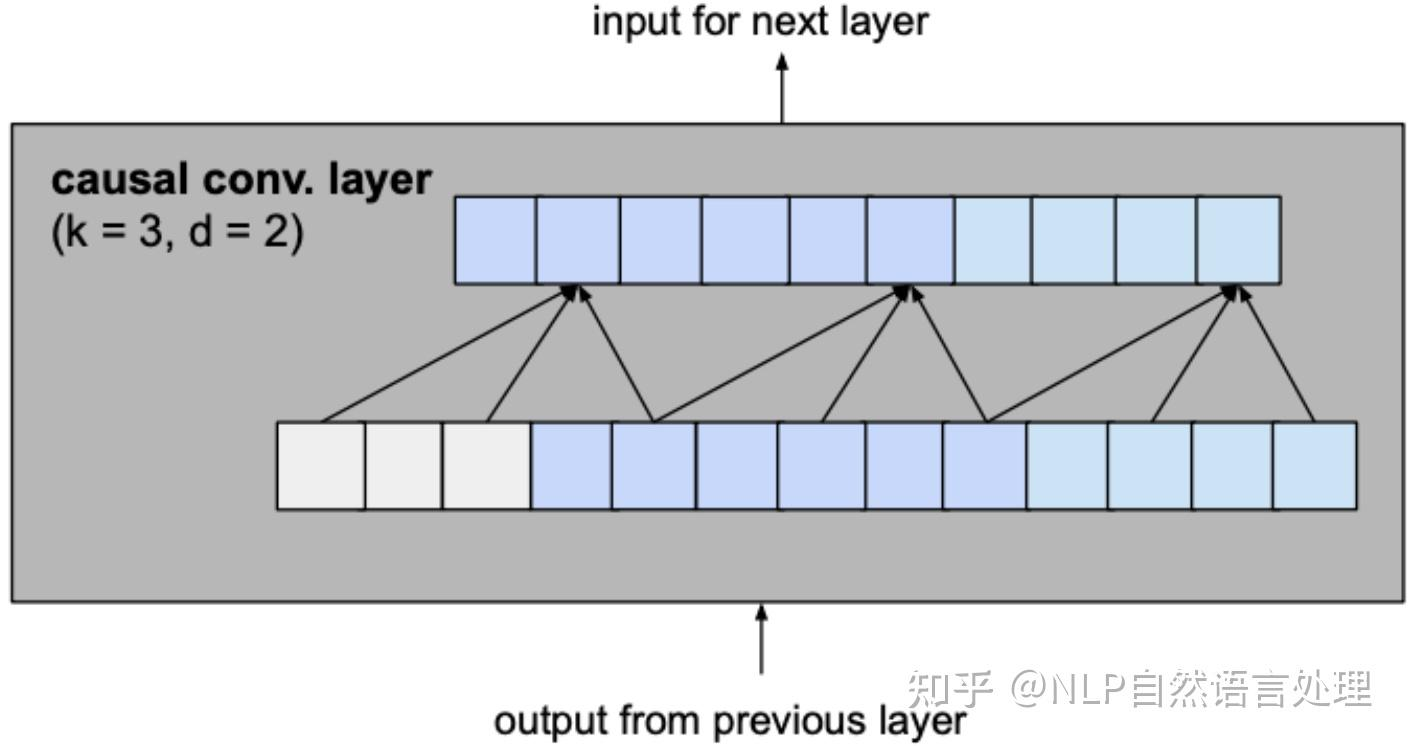
然后变成下图:
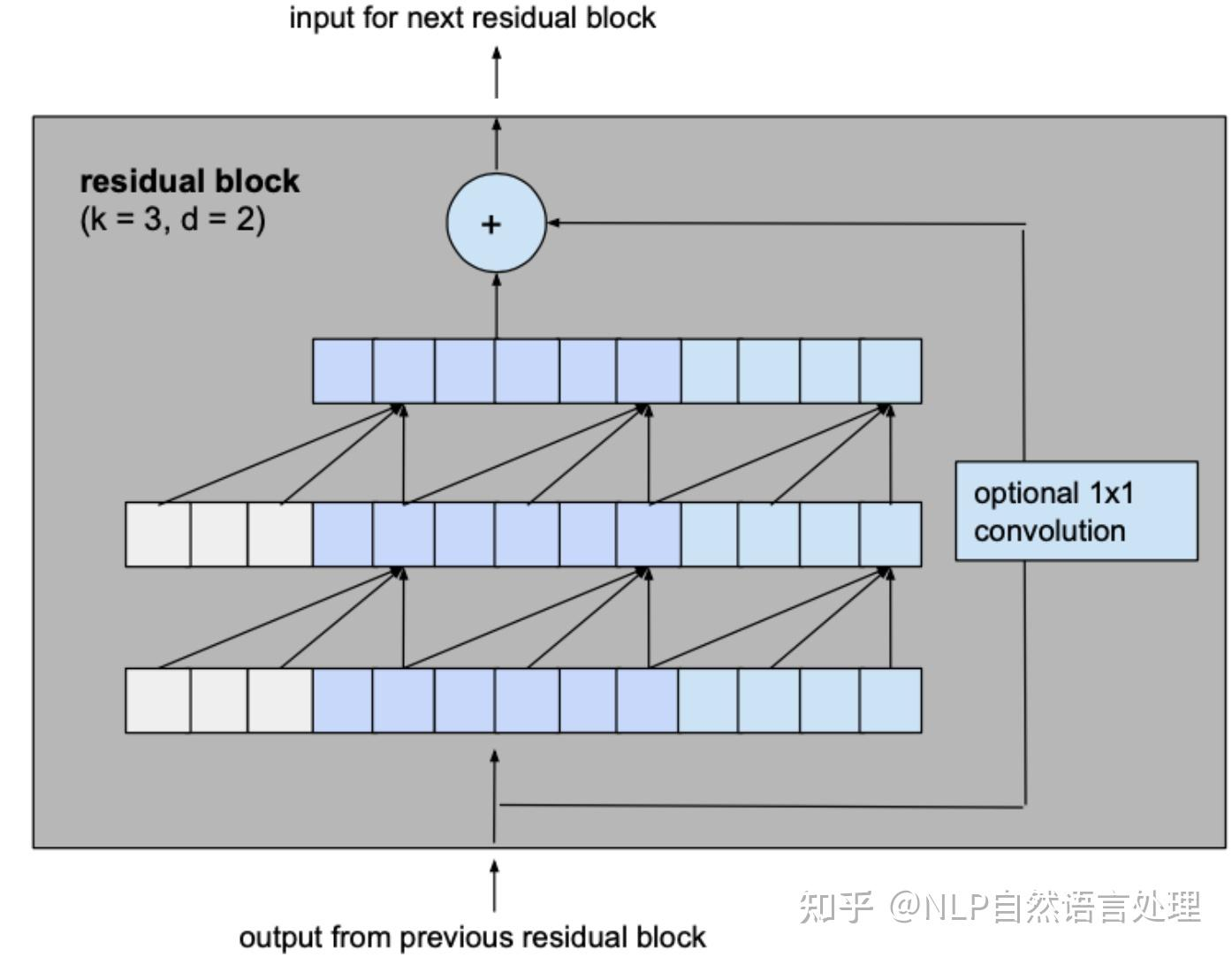
两个卷积层的输出将被添加到残差块的输入中,以产生下一个块的输入。对于网络的所有内部块,即除了第一个和最后一个之外的所有块,输入和输出通道宽度相同,即 num_filters。由于第一个残差块的第一个卷积层和最后一个残差块的第二个卷积层可能具有不同的输入和输出通道宽度,因此可能需要调整残差张量的宽度,这是使用 1×1 卷积完成的.
此更改会影响完全覆盖所需的最小层数的计算。现在我们必须考虑需要多少残差块才能实现完整的感受野覆盖。向 TCN 添加残差块会比添加基本因果层增加两倍的感受野宽度,因为它包括 2 个这样的层。因此,具有扩张基 b 的 TCN 的感受区域 r 的总大小、k ≥ b 的内核大小 k 和残差块的数量 n 可以计算为:
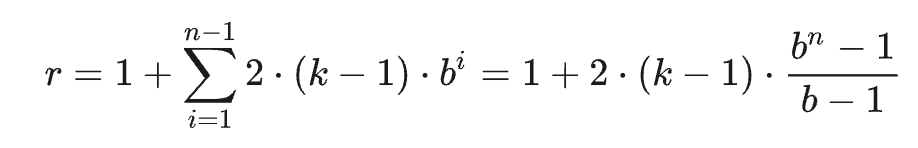
这导致input_length的完整历史覆盖的最小残差块数n为:
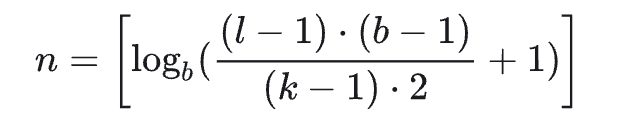
激活、归一、正则化
为了使 TCN 不仅仅是一个过于复杂的线性回归模型,需要在卷积层之上添加激活函数以引入非线性。 ReLU 激活被添加到两个卷积层之后的残差块中。 为了对隐藏层的输入进行归一化(这可以抵消梯度爆炸等问题),将权重归一化应用于每个卷积层。 为了防止过拟合,在每个残差块的每个卷积层之后通过dropout引入正则化。 下图显示了最终的残差块。
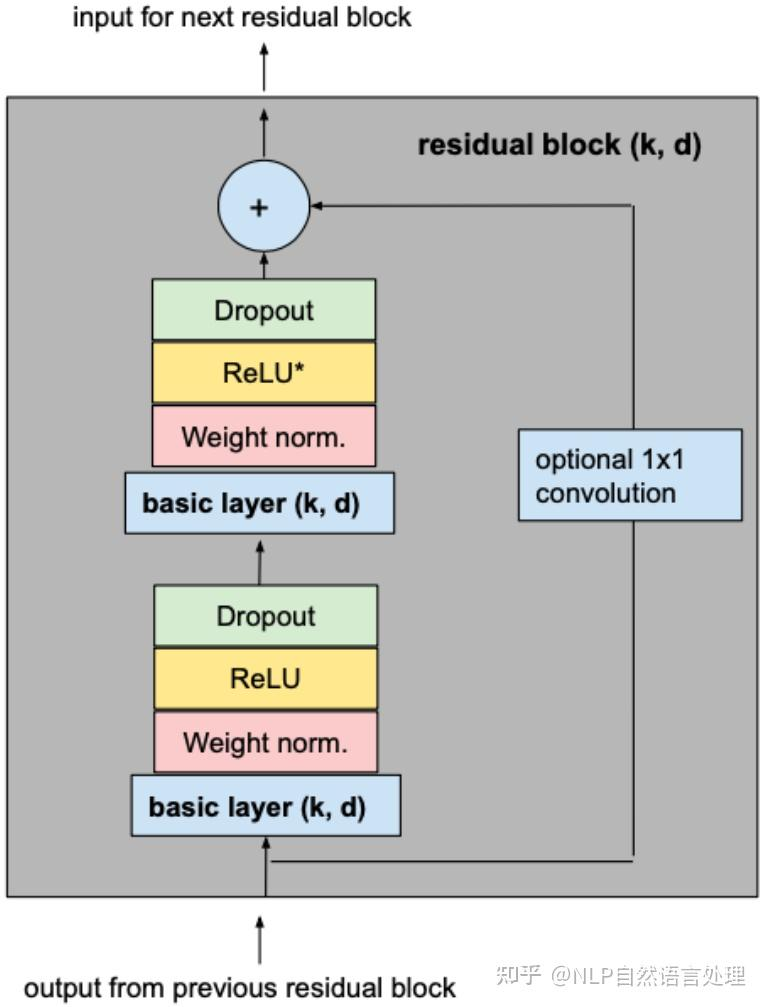
上图中第二个 ReLU 单元中的星号表示它存在于除最后一层之外的每一层,因为我们希望最终输出也能够采用负值(这与论文中概述的架构不同)。
最终模型
下图显示了我们最终的 TCN 模型,其中 l 等于 input_length,k 等于 kernel_size,b 等于 dilation_base,k ≥ b 并且具有完整历史覆盖 n 的最小残差块数,其中n可以根据上面参数计算出来。
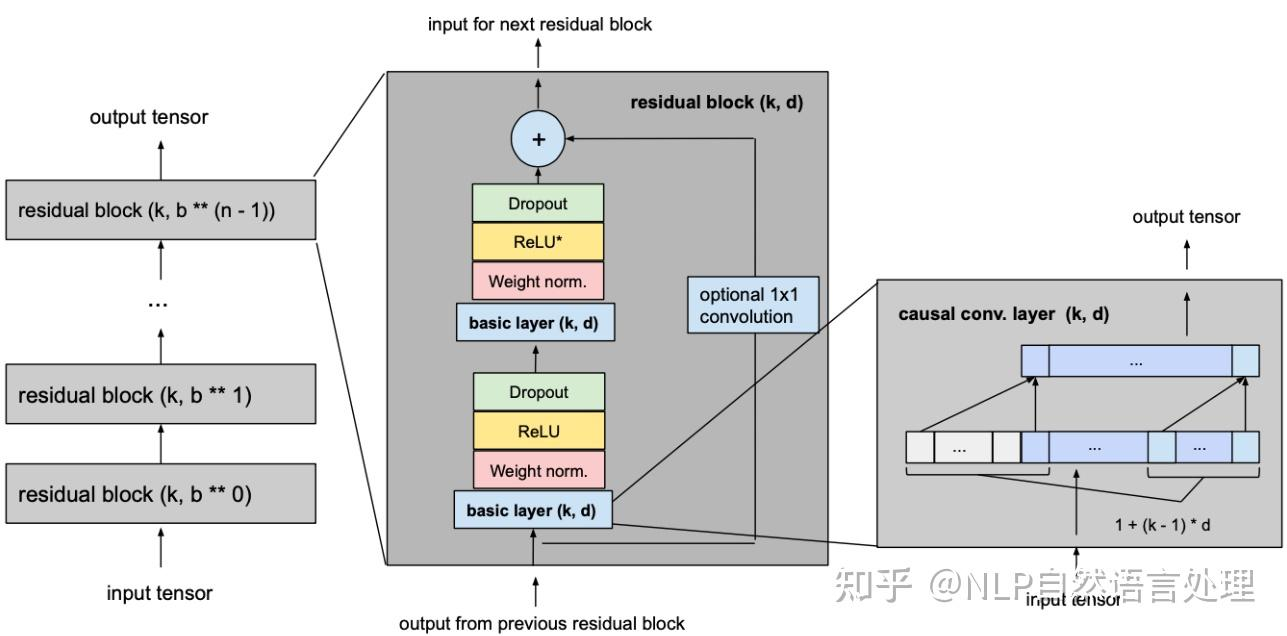
init_weights函数
def init_weights(m): if isinstance(m, nn.Linear): nn.init.xavier_uniform_(m.weight) nn.init.zeros_(m.bias) elif isinstance(m, nn.Conv2d): nn.init.kaiming_uniform_(m.weight) nn.init.zeros_(m.bias)
在深度学习模型的实现中,init_weights函数通常用于初始化模型的权重。权重初始化是训练神经网络的一个重要步骤,它直接影响到模型的训练效率和最终性能。以下是一些常见的权重初始化方法:
随机初始化:
- 随机初始化是最简单的一种权重初始化方法,它通常使用均匀分布或正态分布来生成随机权重。这种方法简单易行,但可能会导致训练过程中的梯度消失或爆炸问题。
Xavier初始化:
- Xavier初始化(也称为Glorot初始化)是一种根据网络层的输入和输出单元数量来调整权重初始化的方法。Xavier初始化可以保持输入和输出的方差一致,从而避免梯度消失或爆炸问题。
He初始化:
- He初始化(也称为Kaiming初始化)是Xavier初始化的变体,它适用于ReLU激活函数。He初始化可以保持输入和输出的方差一致,从而避免梯度消失或爆炸问题。
Kaiming初始化:
- Kaiming初始化是He初始化的另一种称呼,它适用于ReLU激活函数。Kaiming初始化可以保持输入和输出的方差一致,从而避免梯度消失或爆炸问题。
正交初始化:
- 正交初始化是一种将权重矩阵初始化为正交矩阵的方法。正交初始化可以保持输入和输出的方差一致,从而避免梯度消失或爆炸问题。
稀疏初始化:
- 稀疏初始化是一种将权重矩阵初始化为稀疏矩阵的方法。稀疏初始化可以减少模型的参数数量,从而提高模型的泛化能力。
在
init_weights函数中,通常会遍历模型的所有层,并根据层的类型和激活函数选择合适的权重初始化方法。以下是一个简单的
init_weights函数的示例:
1 | def init_weights(m): |
在这个示例中,init_weights函数会检查每个层是否是
nn.Linear或
nn.Conv2d类型,然后根据层的类型选择合适的权重初始化方法。
在深度学习模型的实现中,nn.Linear和
nn.Conv2d是两种最常见的层类型,因此通常只对这两种类型的层进行权重初始化。以下是一些原因:
线性层(
nn.Linear):- 线性层是神经网络中最基本的层类型,它将输入数据映射到输出数据。线性层的权重矩阵通常需要初始化,以便在训练过程中进行有效的更新。
卷积层(
nn.Conv2d):- 卷积层是卷积神经网络中最基本的层类型,它通过卷积操作提取输入数据的特征。卷积层的权重矩阵通常也需要初始化,以便在训练过程中进行有效的更新。
其他层类型:
- 除了线性层和卷积层,神经网络中还有其他类型的层,如激活函数层(如ReLU、Sigmoid等)、池化层(如Max Pooling、Average Pooling等)、归一化层(如Batch Normalization、Layer Normalization等)等。这些层通常不需要初始化权重,因为它们没有可学习的参数。
初始化方法的选择:
- 对于不同的层类型,需要选择合适的权重初始化方法。例如,线性层的权重矩阵通常使用Xavier初始化或He初始化,而卷积层的权重矩阵通常使用Kaiming初始化。
代码简洁性:
- 如果对其他类型的层也进行权重初始化,可能会导致代码变得复杂和冗长。因此,通常只对线性层和卷积层进行权重初始化,以保持代码的简洁性。
总之,nn.Linear和
nn.Conv2d是神经网络中最常见的层类型,因此通常只对这两种类型的层进行权重初始化。
XGBoost
1. 什么是XGBoost
XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
关于GBDT,这里不再提,可以查看我前一篇的介绍,点此跳转。
1.1 XGBoost树的定义
先来举个 例子 ,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
其中:
- 红色箭头所指向的L 即为损失函数(比如平方损失函数:
)
- 红色方框所框起来的是正则项(包括L1正则、L2正则)
- 红色圆圈所圈起来的为常数项
- 对于f(x),XGBoost利用泰勒展开三项,做一个近似。f(x)表示的是其中一颗回归树。
看到这里可能有些读者会头晕了,这么多公式, 我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细 :通俗理解kaggle比赛大杀器xgboost
XGBoost的核心算法思想不难,基本就是:
- 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数 f(x) ,去拟合上次预测的残差。
- 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
- 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
显然,我们的目标是要使得树群的预测值尽量接近真实值
,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
1.2 正则项:树的复杂度
XGBoost对树的复杂度包含了两个部分:
- 一个是树里面叶子节点的个数T
- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
1.3 树该怎么长
很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:枚举所有不同树结构的贪心法
不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是 贪心算法 。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,每次在上一次的预测基础上取最优进一步分裂/建树。
1.4 如何停止树的循环生成
凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
- 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
- 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
- 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
2. XGBoost与GBDT有什么不同
除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
- GBDT是机器学习算法,XGBoost是该算法的工程实现。
- 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
- GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
- 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
- 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
- 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
3. 为什么XGBoost要用泰勒展开,优势在哪里?
XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
4. 代码实现
GitHub:点击进入
损失函数:
在机器学习中,损失函数(Loss Function)是用于衡量模型预测结果与真实结果之间差异的函数。
损失函数的主要作用是评估模型在给定数据上的性能表现。它为模型的优化提供了一个明确的目标,通过最小化损失函数的值,来调整模型的参数,使得模型的预测结果越来越接近真实结果。
不同的机器学习任务通常会使用不同的损失函数。
常见的损失函数:
回归问题:
- 均方误差(Mean Squared Error,MSE):计算预测值与真实值之差的平方的平均值,即 \(\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2\),其中 \(y_i\) 是真实值,\(\hat{y_i}\) 是预测值,\(n\) 是样本数量。
- 平均绝对误差(Mean Absolute Error,MAE):计算预测值与真实值之差的绝对值的平均值,即 \(\frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y_i}|\) 。
分类问题:
- 二分类交叉熵损失(Binary Cross Entropy Loss):常用于二分类问题,如逻辑回归。对于单个样本,其公式为 \(- [y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})]\),其中 \(y\) 是真实标签(0 或 1),\(\hat{y}\) 是预测的概率。
- 多分类交叉熵损失(Categorical Cross Entropy Loss):用于多分类问题,公式为 \(-\sum_{i=1}^{C} y_i \log(\hat{y_i})\),其中 \(C\) 是类别数量,\(y_i\) 是第 \(i\) 类的真实标签(如果样本属于该类为 1,否则为 0),\(\hat{y_i}\) 是模型预测样本属于第 \(i\) 类的概率。
选择合适的损失函数对于模型的训练和性能至关重要。它会影响模型的学习速度、收敛性以及最终的泛化能力。
以下为您介绍几种常见的损失函数:
均方误差(Mean Squared Error,MSE):
- 公式:\(MSE = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y_i})^2\)
- 其中,\(y_i\) 是真实值,\(\hat{y_i}\) 是预测值,\(n\) 是样本数量。
- 常用于回归问题,对较大的误差给予更高的惩罚。
- 例如,预测房价时,如果预测值与真实房价相差较大,MSE 会较大。
平均绝对误差(Mean Absolute Error,MAE):
- 公式:\(MAE = \frac{1}{n} \sum_{i=1}^{n}|y_i - \hat{y_i}|\)
- 同样常用于回归问题,相比 MSE 对异常值更鲁棒。
- 比如,在预测股票价格时,MAE 可能更能承受个别极端价格波动的影响。
交叉熵损失(Cross Entropy Loss):
- 二分类交叉熵:\(L = - [y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})]\) ,其中 \(y\) 是真实标签(0 或 1),\(\hat{y}\) 是预测的概率。
- 多分类交叉熵:\(L = -\sum_{i=1}^{C} y_i \log(\hat{y_i})\) ,其中 \(C\) 是类别数量,\(y_i\) 是第 \(i\) 类的真实标签(如果样本属于该类为 1,否则为 0),\(\hat{y_i}\) 是模型预测样本属于第 \(i\) 类的概率。
- 广泛应用于分类问题,衡量预测概率分布与真实分布之间的差异。
交叉熵损失函数(Cross-Entropy Loss)主要用于衡量模型预测的概率分布与真实的概率分布之间的差异,它在机器学习,特别是深度学习的分类问题中被广泛使用。
其作用主要体现在以下方面:
- 评估模型性能:通过计算预测分布和真实分布之间的差距,来确定模型在分类任务中的表现优劣。交叉熵越小,表示两个概率分布越接近,说明模型的预测结果越接近真实标签,模型的性能也就越好。
- 指导模型优化:在模型训练过程中,交叉熵损失函数的值被用于反向传播,以调整模型的参数,使得损失不断减小,从而使模型的预测逐渐逼近真实标签。
- 处理多分类问题:适用于多类别分类任务,可以方便地处理具有多个类别的情况。对于每个样本,模型输出每个类别的预测概率,而交叉熵损失函数会综合考虑所有类别的预测概率和真实标签来计算损失。

例如,在一个图像分类任务中,模型需要判断图片属于多个类别中的哪一个。模型的输出是每个类别的预测概率,而真实标签则是图片实际所属的类别。通过计算交叉熵损失,可以衡量模型的预测结果与真实类别之间的差异,并利用这个差异来调整模型的参数,以提高模型的分类准确性。
相比其他一些损失函数,交叉熵损失函数具有一些优点,例如易于理解和计算,对噪声数据具有一定的鲁棒性等。然而,它也存在一些缺点,比如对类别不平衡的数据可能较为敏感,在类别不平衡的数据集上,可能会过于关注多数类别而导致模型性能下降;并且它对输出概率分布的平滑性要求较高,如果输出概率分布过于离散,可能会导致损失值较大。

Hinge 损失:
- 常用于支持向量机(SVM)中,特别是在二分类问题中。
- 对于二分类,公式为:\(L = \max(0, 1 - y \cdot \hat{y})\) ,其中 \(y\) 是真实标签(1 或 -1),\(\hat{y}\) 是预测值。
KL 散度(Kullback-Leibler Divergence):
- 用于衡量两个概率分布之间的差异。
- 公式:\(KL(P || Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\)
这些损失函数在不同的机器学习任务和场景中各有优缺点,选择合适的损失函数对于模型的性能和训练效果至关重要。
损失函数的导数计算
以下是几种常见损失函数及其导数的计算方法:

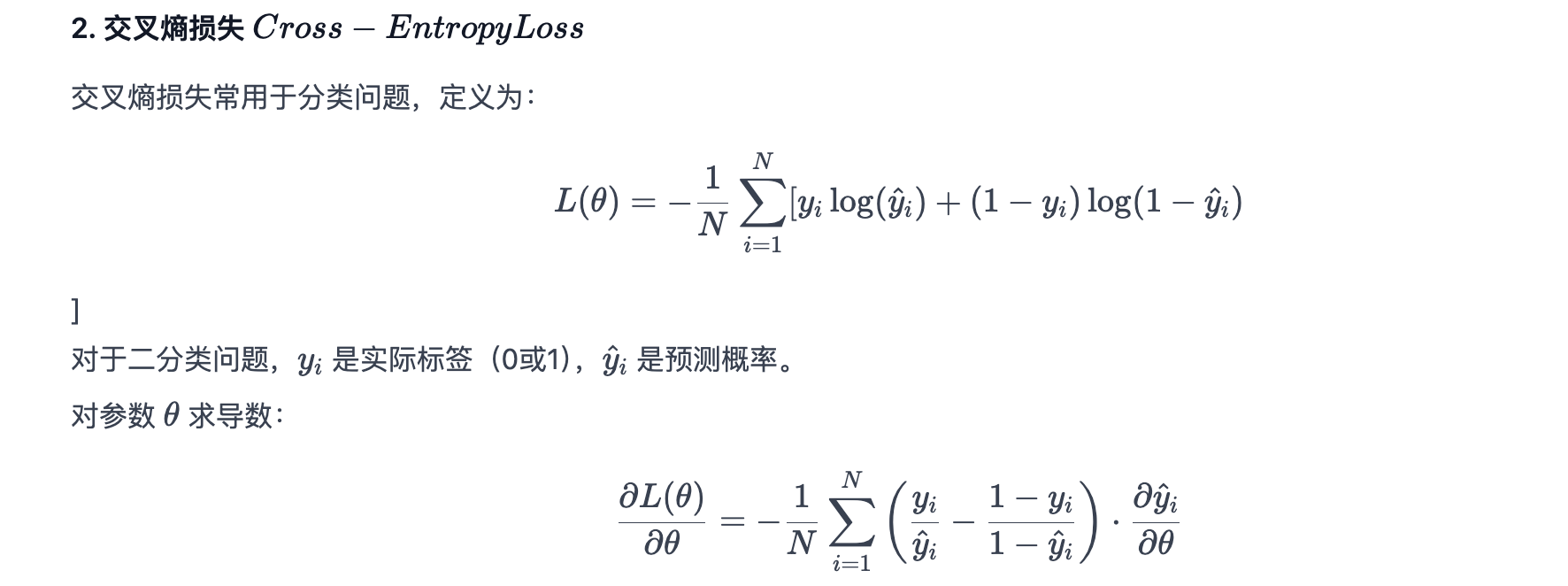

基础不牢,地动山摇,读研到现在有一年多了,发现自己对很多经常打交道的知识并不了解,仅仅是会改一改别人的代码,这使我感到非常焦虑,自此开始我的打基础之路。如果博客中有错误的地方,欢迎大家评论指出,我们互相监督,一起学习进步。
交叉熵损失函数(Cross Entropy Loss)在分类任务中出镜率很高,在代码中也很容易实现,调用一条命令就可以了,那交叉熵是什么东西呢?为什么它可以用来作为损失函数?本文将会循序渐进地解答这些问题,希望能对大家有所帮助。
1. 交叉熵(Cross Entropy)
交叉熵是信息论中的概念,想要理解交叉熵,首先需要了解一些与之相关的信息论基础。
1.1 信息量(本节内容参考《深度学习花书》和《模式识别与机器学习》)
信息量的基本想法是:一个不太可能发生的事件居然发生了,我们收到的信息要多于一个非常可能发生的事件发生。
用一个例子来理解一下,假设我们收到了以下两条消息:
A:今天早上太阳升起
B:今天早上有日食
我们认为消息A的信息量是如此之少,甚至于没有必要发送,而消息B的信息量就很丰富。利用这个例子,我们来细化一下信息量的基本想法:①非常可能发生的事件信息量要比较少,在极端情况下,确保能够发生的事件应该没有信息量;②不太可能发生的事件要具有更高的信息量。事件包含的信息量应与其发生的概率负相关。
假设 是一个离散型随机变量,它的取值集合为
是一个离散型随机变量,它的取值集合为{ x_{1}, x_{2},, x_{n} }"
/>,定义事件X=xiX=xiX=x_i的信息量为:

其中,log表示自然对数,底数为e(也有资料使用底数为2的对数)。公式中, 为变量
为变量 取值为
取值为 的概率,这个概率值应该落在0到1之间,画出上面函数在P为0-1时的取值,图像如下。在概率值
的概率,这个概率值应该落在0到1之间,画出上面函数在P为0-1时的取值,图像如下。在概率值 趋向于0时,信息量趋向于正无穷,在概率值
趋向于0时,信息量趋向于正无穷,在概率值 趋向于1时,信息量趋向于0,这个函数能够满足信息量的基本想法,可以用来描述信息量。
趋向于1时,信息量趋向于0,这个函数能够满足信息量的基本想法,可以用来描述信息量。

1.2 熵(本节内容参考《模式识别与机器学习》)
上面给出的信息量公式只能处理随机变量的取指定值时的信息量,我们可以用香农熵(简称熵)来对整个概率分布的平均信息量进行描述。具体方法为求上述信息量函数关于概率分布 的期望,这个期望值(即熵)为:
的期望,这个期望值(即熵)为:

让我们计算几个例题来对熵有个更深的了解。
例题①:求随机变量 的熵,这个随机变量有8种可能的取值
的熵,这个随机变量有8种可能的取值{ x_{1}, x_{2},...,x_{8} }"
/>,且每种取值发生的概率都是相等的,即:P(X=x1)=P(X=x2)=...=P(X=x8)=18P(X=x1)=P(X=x2)=...=P(X=x8)=18P(X=x_{1})=P(X=x_{2})=...=P(X=x_{8})=\frac{1}{8}
解:

例题②:还是例题①中的随机变量 ,还是8种可能的取值,但是每种取值发生的概率并不是都相等,而是如下所示:
,还是8种可能的取值,但是每种取值发生的概率并不是都相等,而是如下所示: { P(X=x_{1}), P(X=x_{2}),...,P(X=x_{8}) }={
, , , , , ,,}" />
{ P(X=x_{1}), P(X=x_{2}),...,P(X=x_{8}) }={
, , , , , ,,}" />
解:

由例题①和例题②可以佐证《深度学习花书》中的一句结论:那些接近确定性的分布(输出几乎可以确定)具有较低的熵,那些接近均匀分布的概率分布具有较高的熵。
1.3 相对熵(KL散度)(本节内容参考《模式识别与机器学习》)
假设随机变量 的真实概率分布为P(X)P(X)P(X),而我们在处理实际问题时使用了一个近似的分布
的真实概率分布为P(X)P(X)P(X),而我们在处理实际问题时使用了一个近似的分布 来进行建模。由于我们使用的是
来进行建模。由于我们使用的是 而不是真实的P(X)P(X)P(X),所以我们在具体化
而不是真实的P(X)P(X)P(X),所以我们在具体化 的取值时需要一些附加的信息来抵消分布不同造成的影响。我们需要的平均附加信息量可以使用相对熵,或者叫KL散度(Kullback-Leibler
Divergence)来计算,KL散度可以用来衡量两个分布的差异:
的取值时需要一些附加的信息来抵消分布不同造成的影响。我们需要的平均附加信息量可以使用相对熵,或者叫KL散度(Kullback-Leibler
Divergence)来计算,KL散度可以用来衡量两个分布的差异:

下面介绍KL散度的两个性质:
① KL散度不是一个对称量,
② KL散度的值始终 0,当且仅当P(X)=Q(X)P(X)=Q(X)P(X)=Q(X)时等号成立
0,当且仅当P(X)=Q(X)P(X)=Q(X)P(X)=Q(X)时等号成立
1.4 交叉熵
终于到了主角交叉熵了,其实交叉熵与刚刚介绍的KL散度关系很密切,让我们把上面的KL散度公式换一种写法:

交叉熵 就等于:
就等于:
\(H(P,Q)\=H(P)+DKL(P||Q)\=−∑ni\=1P(x_i)logQ(x_i)H(P,Q)\=H(P)+DKL(P||Q)\=−∑i\=1nP(x_i)logQ(x_i)H(P,Q)=H(P)+D\_{KL}(P\left | \right |Q)=-\sum\_{i=1}^{n}P(x\_{i})\log Q(x_{i})\)
也就是KL散度公式的右半部分(带负号)。
细心的小伙伴可能发现了,如果把 看作随机变量的真实分布的话,KL散度左半部分的
看作随机变量的真实分布的话,KL散度左半部分的 其实是一个固定值,KL散度的大小变化其实是由右半部分交叉熵来决定的,因为右半部分含有近似分布
其实是一个固定值,KL散度的大小变化其实是由右半部分交叉熵来决定的,因为右半部分含有近似分布 ,我们可以把它看作网络或模型的实时输出,把KL散度或者交叉熵看做真实标签与网络预测结果的差异,所以神经网络的目的就是通过训练使近似分布
,我们可以把它看作网络或模型的实时输出,把KL散度或者交叉熵看做真实标签与网络预测结果的差异,所以神经网络的目的就是通过训练使近似分布 逼近真实分布
逼近真实分布 。从理论上讲,优化KL散度与优化交叉熵的效果应该是一样的。所以我认为,在深度学习中选择优化交叉熵而非KL散度的原因可能是为了减少一些计算量,交叉熵毕竟比KL散度少一项。
。从理论上讲,优化KL散度与优化交叉熵的效果应该是一样的。所以我认为,在深度学习中选择优化交叉熵而非KL散度的原因可能是为了减少一些计算量,交叉熵毕竟比KL散度少一项。
2. 交叉熵损失函数(Cross Entropy Loss)
刚刚说到,交叉熵是信息论中的一个概念,它与事件的概率分布密切相关,这也就是为什么神经网络在使用交叉熵损失函数时会先使用 函数或者
函数或者 函数将网络的输出转换为概率值。但是据我所知,如果使用PyTorch设计网络的话,它自带的命令torch.nn.functional.cross_entropy已经将转换概率值的操作整合了进去,所以不需要额外进行转换概率值的操作。
函数将网络的输出转换为概率值。但是据我所知,如果使用PyTorch设计网络的话,它自带的命令torch.nn.functional.cross_entropy已经将转换概率值的操作整合了进去,所以不需要额外进行转换概率值的操作。
下面从两个方面讨论交叉熵损失函数:
2.1 交叉熵损失函数在单标签分类任务中的使用(二分类任务包含在其中)
单标签任务,顾名思义,每个样本只能有一个标签,比如ImageNet图像分类任务,或者MNIST手写数字识别数据集,每张图片只能有一个固定的标签。
对单个样本,假设真实分布为 ,网络输出分布为
,网络输出分布为 ,总的类别数为
,总的类别数为 ,则在这种情况下,交叉熵损失函数的计算方法为:
,则在这种情况下,交叉熵损失函数的计算方法为:

用一个例子来说明,在手写数字识别任务中,如果样本是数字“5”,那么真实分布应该为:
\[ 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 \]
,
如果网络输出的分布为:
\[ 0.1, 0.1, 0, 0, 0, 0.7, 0, 0.1, 0, 0 \]
,则 应为10,那么计算损失函数得:
应为10,那么计算损失函数得:

如果网络输出的分布为:
\[ 0.2, 0.3, 0.1, 0, 0, 0.3, 0.1, 0, 0, 0 \]
,那么计算损失函数得:

上述两种情况对比,第一个分布的损失明显低于第二个分布的损失,说明第一个分布更接近于真实分布,事实也确实是这样。
对一个batch,单标签n分类任务的交叉熵损失函数的计算方法为:
 函数作为网络最后一层的输出,把网络最后一层的每个神经元都看做任务中的一个类别,以图像识别任务为例,网络最后一层的输出应该理解为:网络认为图片中含有这一类别物体的概率。而每一类的真实标签都只有两种可能值,即“图片中含有这一类物体”和“图片中不含有这一类物体”,这是一个二项分布。综上所述,对多分类任务中的每一类单独分析的话,真实分布
函数作为网络最后一层的输出,把网络最后一层的每个神经元都看做任务中的一个类别,以图像识别任务为例,网络最后一层的输出应该理解为:网络认为图片中含有这一类别物体的概率。而每一类的真实标签都只有两种可能值,即“图片中含有这一类物体”和“图片中不含有这一类物体”,这是一个二项分布。综上所述,对多分类任务中的每一类单独分析的话,真实分布 是一个二项分布,可能的取值为0或者1,而网络预测的分布
是一个二项分布,可能的取值为0或者1,而网络预测的分布 可以理解为标签是1的概率。此外,由于多标签分类任务中,每一类是相互独立的,所以网络最后一层神经元输出的概率值之和并不等于1。对多标签分类任务中的一类任务来看,交叉熵损失函数为:
可以理解为标签是1的概率。此外,由于多标签分类任务中,每一类是相互独立的,所以网络最后一层神经元输出的概率值之和并不等于1。对多标签分类任务中的一类任务来看,交叉熵损失函数为:

总的交叉熵为多标签分类任务中每一类的交叉熵之和。
让我们用一个例子来理解一下,如下图所示,图中有米饭和一些菜品,假设当前的多标签分类任务有三个标签:米饭、南瓜、青菜。很明显,左边这张图是没有青菜的,它的真实分布应该为:
\[ 1, 1, 0 \]
。

情况①:假设经过右图的网络输出的概率分布为:
\[ 0.8, 0.9, 0.1 \]
,则我们可以对米饭、南瓜、青菜这三类都计算交叉熵损失函数,然后将它们相加就得到这一张图片样本的交叉熵损失函数值。



情况②:假设经过右图的网络输出的概率分布为:
\[ 0.3, 0.5, 0.7 \]
,同样计算交叉熵损失函数:




由上面两种情况也可以看出,预测分布越接近真实分布,交叉熵损失越小,预测分布越远离真实分布,交叉熵损失越大。
对一个batch,多标签n分类任务的交叉熵损失函数的计算方法为:

生成模型和概率模型的主要区别
同样是通过 X 估计 Y
判别模型是通过构建条件概率p(y |x)来生成 y 的估计
而生成模型则会通过生成联合概率分布(这是区分是不是生成模型最本质的标准)来估计,而在p(x,y)已经知道的情況下,p(yIx)就可以由p(xy)除以p(x)构建
或者说
生成模型:学习得到联合概率分布P(x,y),即特征x和标记y共同出现的概率,然后求条件概率分布。能够学习到数据生成的机制。特点是会在学习中试图去生成新的 x
判别模型:学习得到条件概率分布P(y|x),即在特征x出现的情况下标记y出现的概率。


NCE 噪声对比损失

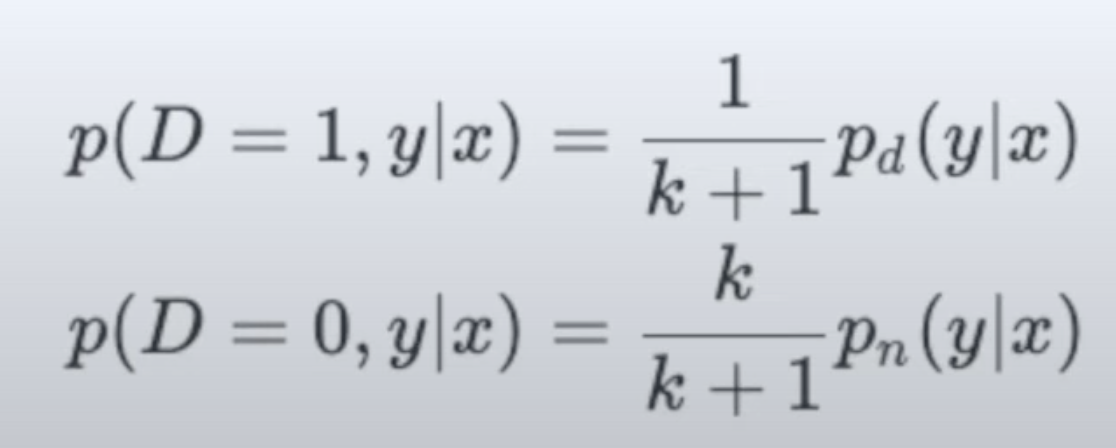
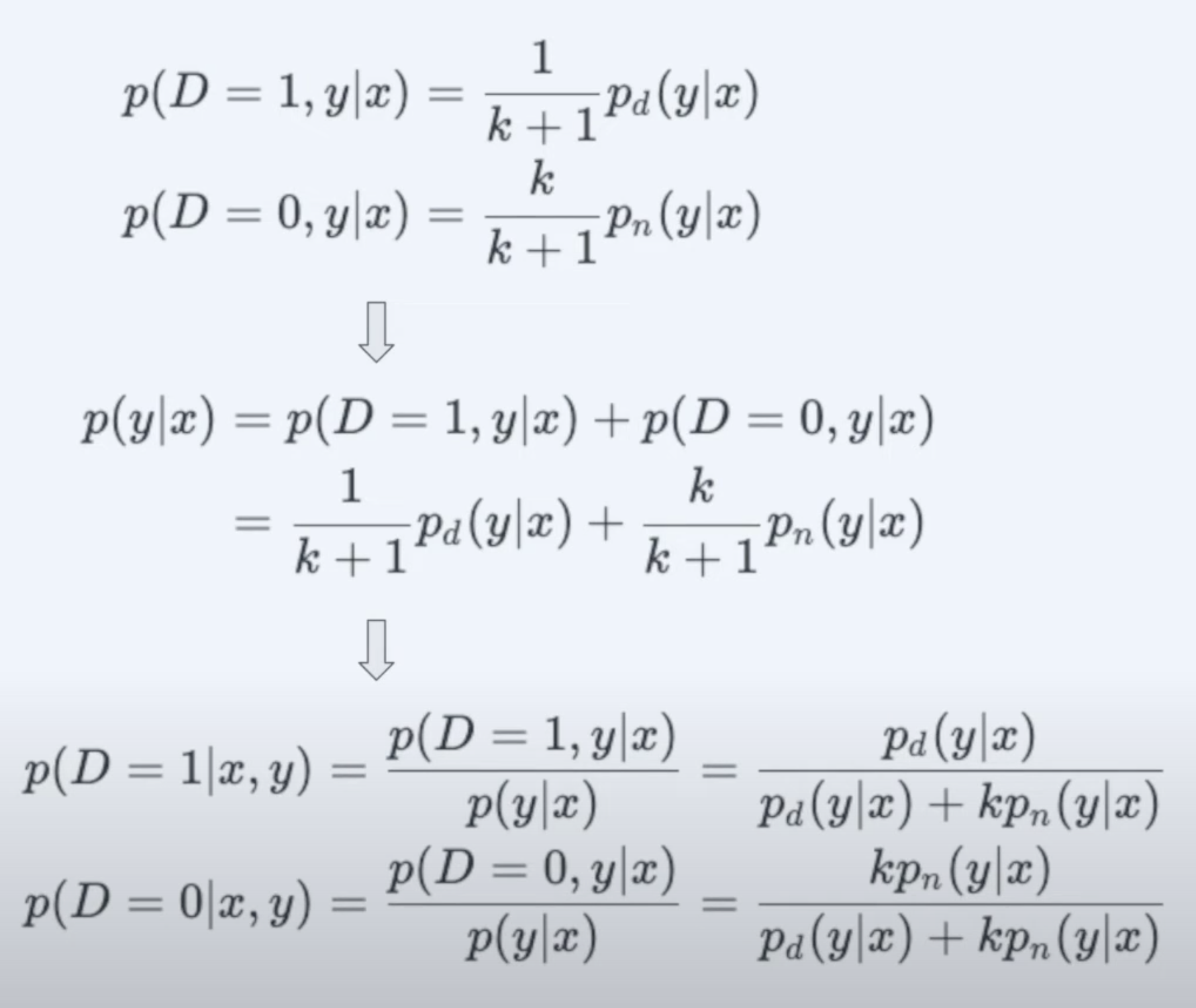





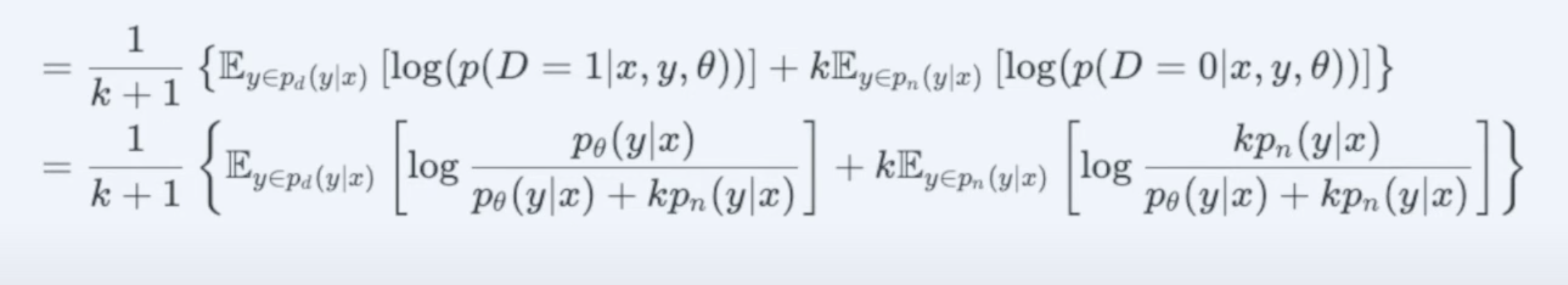
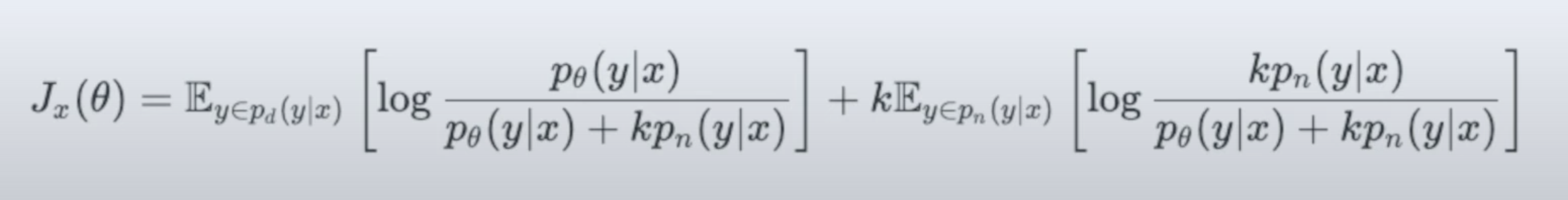



监督对比损失(Supervised Contrastive Loss)
监督对比损失(Supervised Contrastive Loss)是一种在深度学习中用于有监督学习任务的损失函数,主要用于提高模型对相似样本的区分能力和对不同类别样本的聚类效果。
一、基本原理
监督对比损失的核心思想是在有标签信息的情况下,通过拉近同一类别的样本之间的距离,同时推远不同类别的样本之间的距离,从而使模型学习到更具判别性的特征表示。
具体来说,对于一个包含多个样本的批次,首先计算每个样本的特征向量。然后,对于每个样本,找到与其具有相同标签的正样本和不同标签的负样本。接着,计算该样本与正样本和负样本之间的相似度,通常使用余弦相似度或点积等方法。最后,根据相似度计算监督对比损失,使得正样本之间的相似度尽可能高,负样本之间的相似度尽可能低。
二、计算方法
假设一个批次中有 \(N\) 个样本,每个样本的特征向量为 \(h_i\),对应的标签为 \(y_i\)。监督对比损失的计算公式如下:
\(L_{contrastive}=\frac{1}{2N}\sum_{i=1}^{N}[l(1-s(h_i,h_{pos(i)}))+\sum_{j=1,j\neq i}^{N}l(s(h_i,h_{neg(j)}))]\)
其中,\(h_{pos(i)}\) 表示与样本 \(i\) 具有相同标签的正样本的特征向量,\(h_{neg(j)}\) 表示与样本 \(i\) 具有不同标签的负样本的特征向量,\(s(\cdot,\cdot)\) 表示相似度函数,通常为余弦相似度,\(l(x)=-\log\frac{e^{x/T}}{e^{x/T}+\sum_{k=1,k\neq i}^{N}e^{s(h_i,h_{neg(k)})/T}}\) 是一个损失函数,\(T\) 是一个温度参数,用于控制相似度的缩放。
三、作用和优势
提高特征表示的判别性
- 通过强制同一类别的样本靠近,不同类别的样本远离,监督对比损失可以使模型学习到更具判别性的特征表示,从而提高模型在分类、聚类等任务中的性能。
增强模型的鲁棒性
- 对数据中的噪声和异常值具有一定的鲁棒性,因为它关注的是样本之间的相对关系,而不是绝对的值。
适用于大规模数据集
- 可以有效地处理大规模数据集,因为它可以在批次内进行计算,不需要对整个数据集进行计算。
与其他损失函数结合使用
- 可以与其他损失函数(如交叉熵损失)结合使用,以进一步提高模型的性能。
四、应用场景
图像分类
- 在图像分类任务中,监督对比损失可以帮助模型学习到更具判别性的图像特征,提高分类准确性。
自然语言处理
- 例如文本分类、情感分析等任务中,监督对比损失可以使模型更好地理解文本的语义,提高任务的性能。
推荐系统
- 通过学习用户和物品的特征表示,监督对比损失可以提高推荐系统的准确性和个性化程度。
激活函数:
在神经网络中,激活函数是一种对神经元的输入进行非线性变换的函数。
激活函数的主要作用包括:
- 引入非线性:如果没有激活函数,神经网络仅仅是对输入进行线性组合,其表达能力非常有限,无法处理复杂的非线性问题。通过引入非线性的激活函数,可以使神经网络能够拟合各种复杂的函数和模式。
- 控制神经元的输出范围:不同的激活函数会将输入映射到不同的输出范围,例如
Sigmoid函数将输出限制在(0, 1)之间,Tanh函数将输出限制在(-1, 1)之间。 - 增加网络的稀疏性:某些激活函数,如
ReLU(Rectified Linear Unit),当输入为负数时输出为 0,这有助于在网络中引入稀疏性,减少计算量,并可能有助于防止过拟合。
常见的激活函数有:
Sigmoid函数:f(x) = 1 / (1 + e^(-x)),输出范围在(0, 1)之间,常用于二分类问题的输出层。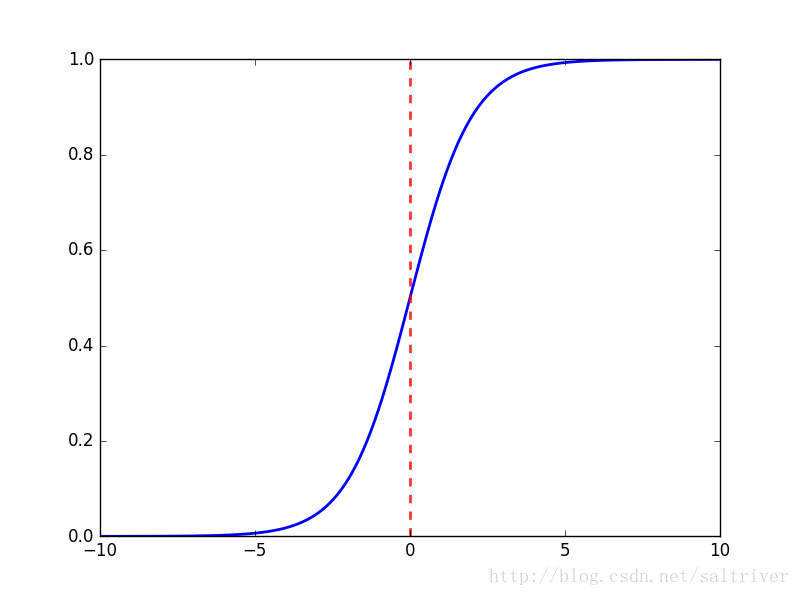
可以看出,sigmoid函数连续,光滑,严格单调,以(0,0.5)中心对称,是一个非常良好的阈值函数。

Tanh函数:f(x) = (e^x - e^(-x)) / (e^x + e^(-x)),输出范围在(-1, 1)之间。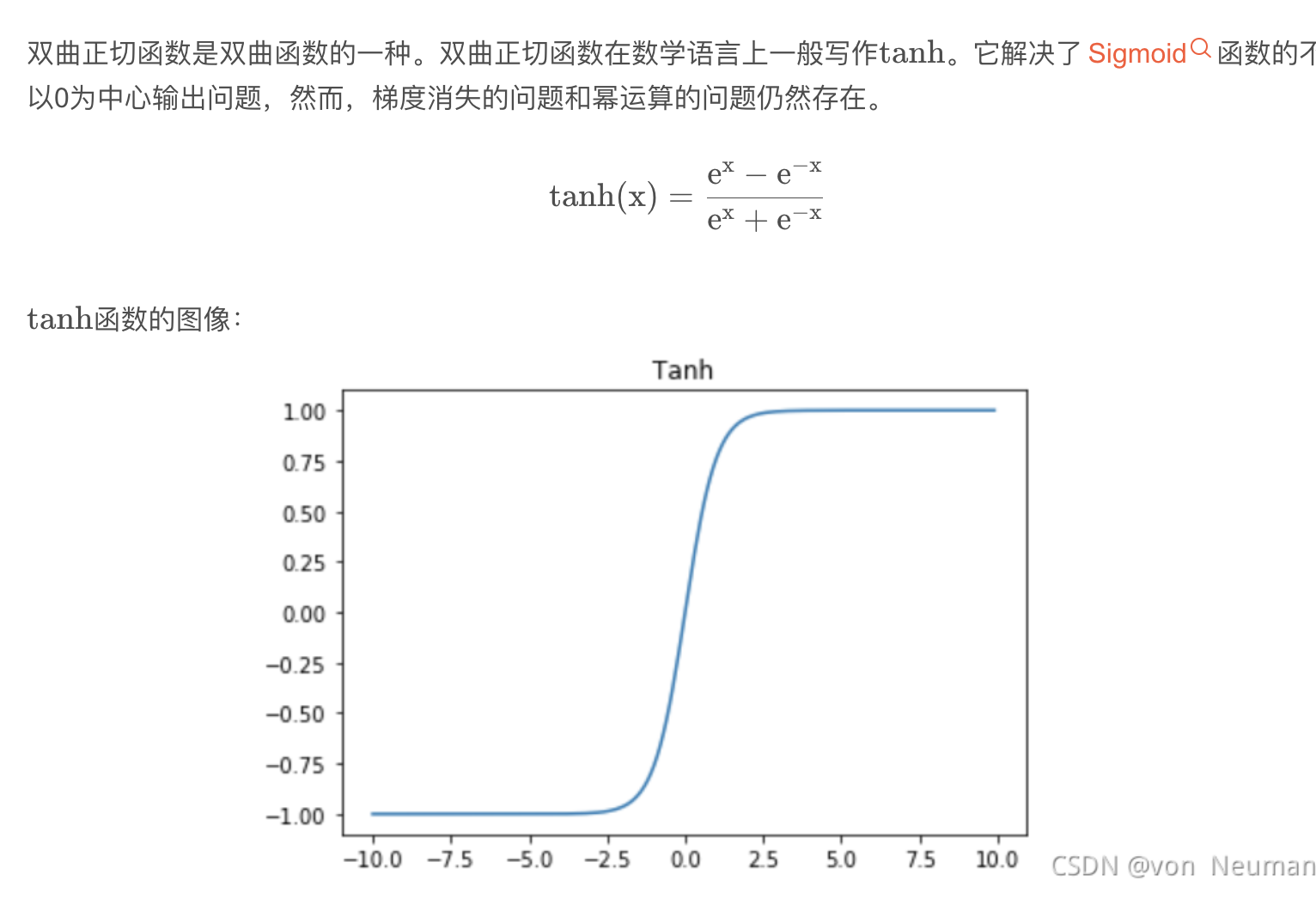
ReLU函数:f(x) = max(0, x),计算简单,在很多深度神经网络中广泛使用。 线性整流函数,又称修正线性单元ReLU,是一种人工神经网络中常用的激活函数,通常指代以斜坡函数及其变种为代表的非线性函数。线性整流函数(ReLU函数)的特点:
当输入为正时,不存在梯度饱和问题。 计算速度快得多。ReLU 函数中只存在线性关系,因此它的计算速度比Sigmoid函数和tanh函数更快。 Dead ReLU问题。当输入为负时,ReLU完全失效,在正向传播过程中,这不是问题。有些区域很敏感,有些则不敏感。但是在反向传播过程中,如果输入负数,则梯度将完全为零,Sigmoid函数和tanh函数也具有相同的问题 ReLU函数的输出为0或正数,这意味着ReLU函数不是以0为中心的函数。
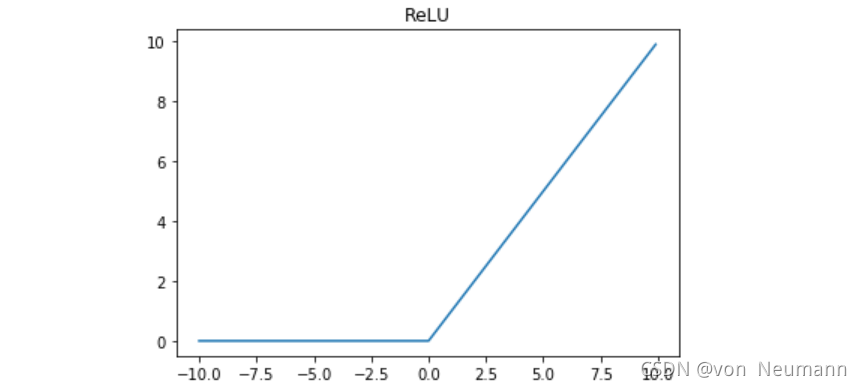
https://medium.com/machine-intelligence-report/how-do-neural-networks-work-57d1ab5337ce
为什么说ReLU是非线性激活函数?
relu的两个分段函数,分段来看,确实是线性,组合在一起,整体却不是线性的 。
线性在二维空间中的定义是一条直线能够将平面空间划分,如下图所示:
当加了一个relu之后 :
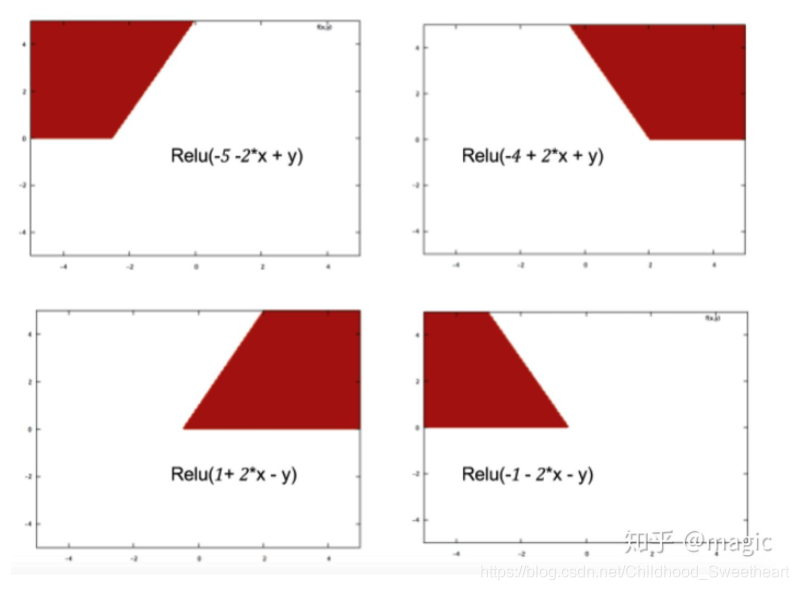
当几个ReLU函数组合到一起的时候,就变成非线性的:
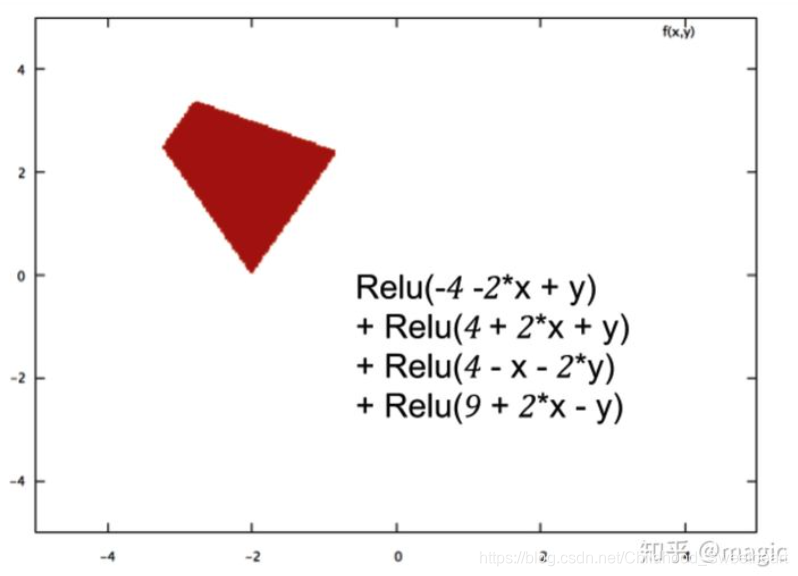
我认为还是取决于输入 如果输入导致后面的输入大部分都是正的 哪relu可能就会表现出线性,但只要有负的,传递过程就会变得非线性 而且负的越多 非线性程度就越大(所以浅层的一般不用relu) 正因为出现负的这种可能性 relu才表现出他的非线性功能。
Leaky ReLU函数:f(x) = max(0.01x, x),是ReLU的改进版,解决了ReLU中神经元可能“死亡”的问题。
为什么说ReLU是非线性激活函数
为什么说ReLU是非线性激活函数
为什么说ReLU是非线性激活函数
Leaky ReLU函数的特点:
Leaky ReLU函数通过把x xx的非常小的线性分量给予负输入0.01 x
0.01x0.01x来调整负值的零梯度问题。 Leaky有助于扩大ReLU函数的范围,通常α
0.01左右。 Leaky ReLU的函数范围是负无穷到正无穷。 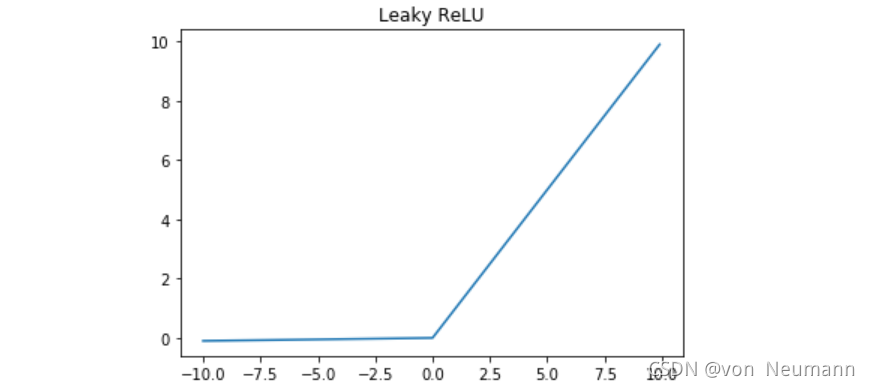
下面是一个使用 Sigmoid 激活函数的简单示例代码:
1 | import numpy as np |
激活函数的选择对神经网络的性能有很大影响,需要根据具体问题和网络结构进行合适的选择。
常见的激活函数:
Sigmoid 函数:
- 数学表达式:
f(x) = 1 / (1 + e^(-x)) - 特点:将输入值压缩到 0 到 1
之间,具有平滑的曲线。但在输入值较大或较小时,梯度接近
0,可能导致梯度消失问题。

- 数学表达式:
Tanh 函数:
- 数学表达式:
f(x) = (e^x - e^(-x)) / (e^x + e^(-x)) - 特点:将输入值压缩到 -1 到 1 之间,相比 Sigmoid 函数,以 0 为中心。

- 数学表达式:
ReLU 函数(Rectified Linear Unit):
- 数学表达式:
f(x) = max(0, x) - 特点:计算简单,在正半轴上梯度恒为
1,有效缓解了梯度消失问题。但存在神经元“死亡”的可能,即输入为负时永远不被激活。

- 数学表达式:
Leaky ReLU 函数:
- 数学表达式:
f(x) = max(ax, x),其中a是一个较小的正数(如 0.01) - 特点:对 ReLU 进行改进,解决了神经元“死亡”的问题。

- 数学表达式:
ELU 函数(Exponential Linear Unit):
- 数学表达式:
f(x) = x if x > 0 else a(e^x - 1),其中a是一个常数 - 特点:具有 ReLU 的优点,同时在输入为负时输出不为 0,使得平均输出更接近 0。
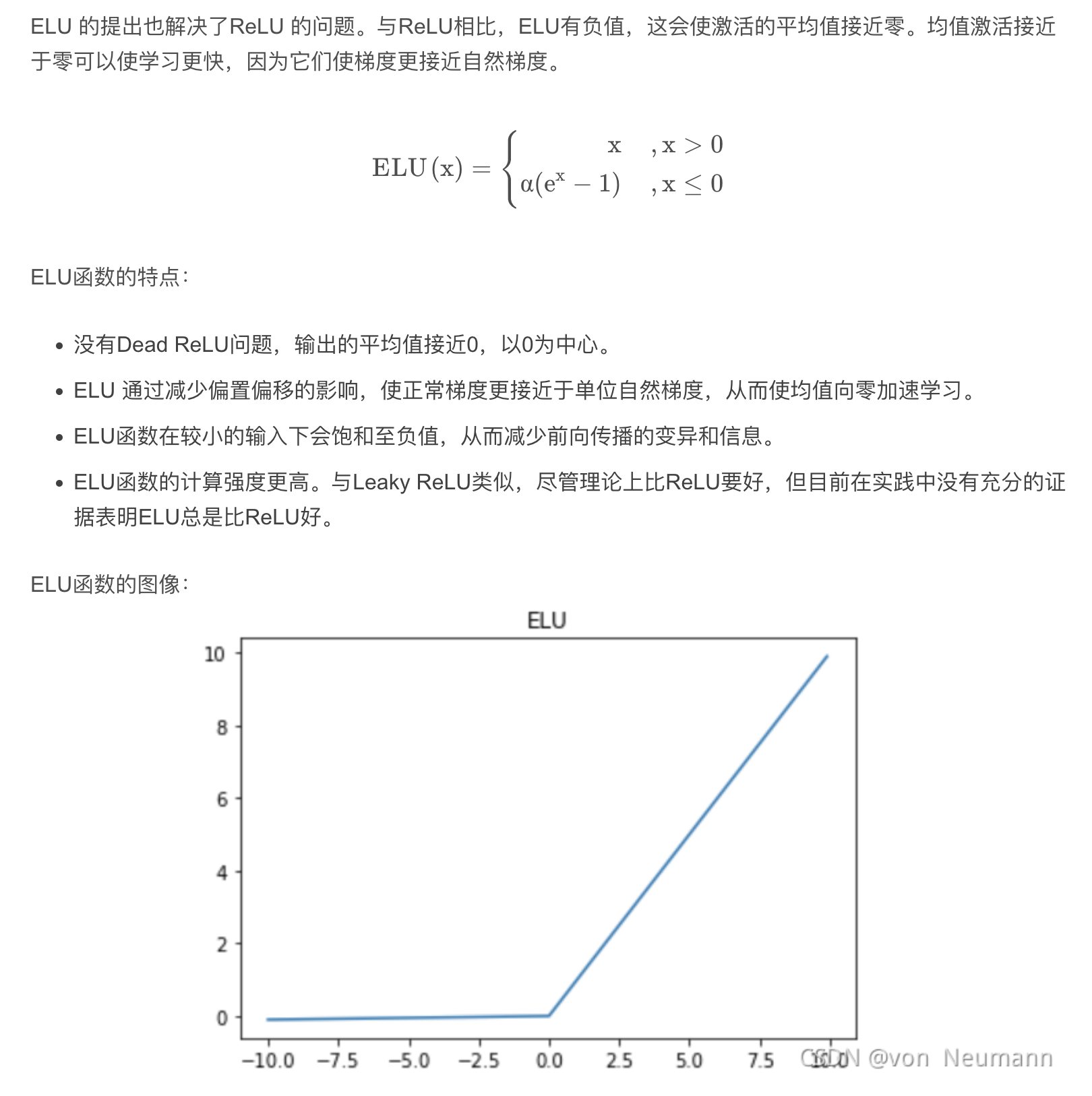
- 数学表达式:
Softmax 函数:
- 常用于多分类问题的输出层,将多个神经元的输出值映射为概率分布。
以下是一个使用 Python 绘制部分常见激活函数图像的示例代码:
1 | import numpy as np |
不同的激活函数在不同的场景和网络结构中表现各异,需要根据具体问题进行选择和调整。
学习率
学习率(Learning Rate)在机器学习中是一个非常关键的超参数。
学习率决定了模型在训练过程中参数更新的步长大小。
较小的学习率意味着模型在参数更新时采取较小的步幅,可能会使训练过程更加稳定,但收敛速度较慢,需要更多的训练迭代次数才能达到较好的效果。
例如,如果学习率过小,如 0.0001 ,模型可能会在训练中进展缓慢,需要大量的训练轮数才能逐渐优化参数。
较大的学习率会使模型在参数更新时采取较大的步幅,可能会加快收敛速度,但也可能导致模型跳过最优解,甚至无法收敛。
比如,学习率过大,如 10 ,模型可能会在训练中出现剧烈的波动,无法稳定地优化参数。
选择合适的学习率通常需要通过试验和错误来确定。常见的方法包括使用固定的学习率、学习率衰减(随着训练的进行逐渐减小学习率)、自适应学习率算法(如 Adam 优化器中的自适应学习率调整)等。
例如,在深度学习中,训练开始时可以使用较大的学习率,如 0.1 ,然后随着训练的进行,逐渐将学习率减小到 0.001 ,以实现更精细的参数调整和更好的收敛效果。
以下是一些常见的学习率调整方法:
固定学习率:在整个训练过程中保持学习率不变。这种方法简单,但可能不是最优的,因为在训练的不同阶段可能需要不同的学习率。
分段常数学习率:将训练过程分为几个阶段,每个阶段使用不同的固定学习率。例如,在前几个 epoch 使用较大的学习率,然后在后续阶段使用较小的学习率。
学习率衰减:
- 按步长衰减:每隔一定的训练步数或 epoch,将学习率乘以一个小于 1 的衰减因子。
- 指数衰减:学习率按照指数形式衰减,例如
learning_rate = initial_learning_rate * decay_rate ^ (epoch / decay_steps)。 - 多项式衰减:学习率按照多项式的形式逐渐减小。
自适应学习率算法:
- Adagrad:根据每个参数之前的梯度历史来调整学习率,对于不常更新的参数给予较大的学习率,对于频繁更新的参数给予较小的学习率。
- Adadelta:是对 Adagrad 的改进,避免了学习率单调递减的问题。
- RMSProp:类似于 Adadelta,对梯度的二阶矩进行指数加权平均来调整学习率。
- Adam:结合了动量和 RMSProp 的优点,能够自适应地调整学习率。
余弦退火:学习率按照余弦函数的形式进行周期性的变化,在每个周期内从较高的值逐渐降低到较低的值,然后再上升。
基于验证集性能调整:根据模型在验证集上的性能来动态调整学习率。如果验证集性能在一段时间内没有改善,就降低学习率。
这些方法各有优缺点,具体选择哪种方法取决于数据集、模型架构和训练需求等因素。通常需要通过实验来找到最适合特定问题的学习率调整策略。
optimizer的概念
https://www.bilibili.com/video/BV1jh4y1q7ua/?vd_source=69d49a91e3d96bad6e2f1ea1eb1f6c22
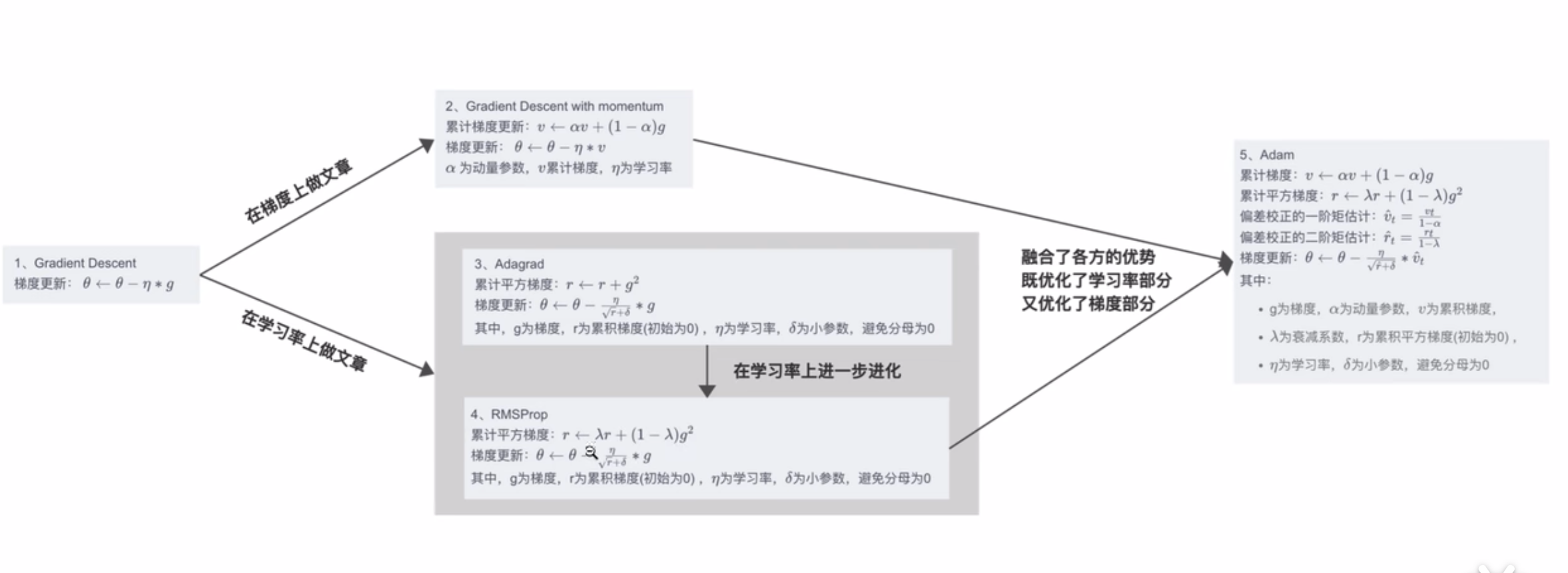
在机器学习中,optimizer(优化器)是用于调整模型参数以最小化损失函数或最大化目标函数的算法或策略。
优化器的主要作用是根据损失函数计算的梯度,按照特定算法(如SGD、Adam等)更新模型权重
常见的优化器有随机梯度下降(Stochastic Gradient Descent,SGD)、Adagrad、Adadelta、RMSprop、Adam 等。
以随机梯度下降(SGD)为例,它的基本思想是沿着梯度的反方向,以一定的学习率来更新参数。假设参数为
w ,梯度为 g ,学习率为 lr
,则更新公式为 w = w - lr * g 。
Adagrad 则根据每个参数之前的梯度历史来自适应地调整学习率。对于频繁更新的参数,学习率会逐渐减小,而对于很少更新的参数,学习率会相对较大。
RMSprop 类似于 Adagrad,但它不是累积所有的梯度平方,而是使用指数加权平均来计算梯度平方的估计值。
Adam 结合了动量和 RMSprop 的优点,同时考虑了梯度的一阶矩和二阶矩来动态调整学习率。
AdamW是Adam优化器的权重衰减版本,它将权重衰减直接集成到优化器中,而不是在训练过程中单独应用权重衰减。 AdamW通常比Adam表现更好,因为它可以更好地处理权重衰减。在相同的权重衰减值下,AdamW的正则化效果更强。
选择合适的优化器对于模型的训练效率和最终性能至关重要。例如,在数据量较大且模型较复杂时,Adam 通常能取得较好的效果;而在一些简单的模型和小数据集上,SGD 可能表现不错,并且通过适当的调整学习率等超参数,也能获得较好的结果。
再比如,在处理具有稀疏特征的问题时,Adagrad 可能更合适。总之,优化器的选择需要根据具体的问题和数据特点来决定,并可能需要通过实验来找到最优的选择。
使用方法
1 | # 创建优化器 |
optimizer的内部结构
看了就懂原理了
1 | # PyTorch优化器的基本结构 |
lr_scheduler的概念
- 功能 :动态调整学习率
- 作用 :根据预设策略(如阶梯式衰减、余弦退火等)在训练过程中改变学习率
- 目标 :提高训练效率和模型性能,避免学习率过大或过小导致的问题
使用的方法
1 | # 创建学习率调度器 |
optimizer.step() 和 lr_scheduler.step() 的区别
optimizer.step()
- 功能 :根据反向传播计算的梯度更新模型参数
- 调用时机 :每个小批量(batch)训练后调用
- 作用 :执行一步梯度下降,更新模型权重
- 频率 :通常每个batch调用一次
lr_scheduler.step()
- 功能 :根据预设策略调整学习率
- 调用时机 :通常在每个epoch结束后调用(也有按batch调整的策略)
- 作用 :修改optimizer中的学习率参数
- 频率 :通常每个epoch调用一次
理解权重衰减系数和动量系数
权重衰减系数 (Weight Decay)
权重衰减是一种正则化技术,用于防止模型过拟合。在深度学习中,它的工作原理和应用如下:
基本概念
- 权重衰减系数通常表示为
weight_decay或wd - 在您的代码中表示为
cfg.TRAIN.WD - 典型值范围:0.0001 (1e-4) 到 0.01 (1e-2)
工作原理
传统实现(L2正则化):
- 在损失函数中添加一项:
loss += weight_decay * ||w||² - 其中
||w||²是权重参数的平方和
- 在损失函数中添加一项:
AdamW 中的实现:
- 直接在权重更新步骤中应用:
w = w - lr * (gradient + weight_decay * w) - 这种方式与自适应学习率解耦,效果更好
- 直接在权重更新步骤中应用:
作用
- 限制模型权重的大小,防止某些权重变得过大
- 使模型更加"平滑",提高泛化能力
- 减少过拟合,特别是在训练数据有限时
如何选择
- 较大的值(如0.01):更强的正则化,适用于小数据集或简单模型
- 较小的值(如0.0001):较弱的正则化,适用于大数据集或复杂模型
- 通常需要通过交叉验证来确定最佳值
动量系数 (Momentum)
动量是优化算法中的一个重要概念,用于加速训练并帮助跳出局部最小值。
基本概念
- 在SGD中表示为
momentum参数 - 在您的代码中表示为
cfg.TRAIN.MOMENTUM - 在Adam/AdamW中表示为
betas参数的两个值 - 典型值:SGD中为0.9,Adam中为(0.9, 0.999)
工作原理
SGD中的动量:
- 记录之前的更新方向:
v_t = momentum * v_{t-1} + learning_rate * gradient - 更新参数:
parameter = parameter - v_t - 类似于物理中的动量,保持一定的移动"惯性"
- 记录之前的更新方向:
Adam/AdamW中的动量(betas):
- 第一个值(0.9):控制梯度的移动平均(一阶矩)
- 第二个值(0.999):控制梯度平方的移动平均(二阶矩)
- 结合这两个值来自适应调整每个参数的学习率
作用
- 加速收敛,特别是在平坦区域
- 帮助跳出局部最小值
- 减少训练过程中的震荡
- 使更新方向更加稳定
如何选择
- SGD中,0.9是常用值,表示当前梯度占10%,历史动量占90%
- 较大的值(如0.99):更强的惯性,可能跳过局部最小值
- 较小的值(如0.5):更关注当前梯度,对噪声更敏感
- Adam中的默认值(0.9, 0.999)通常表现良好,很少需要调整
两者的区别与联系
目的不同:
- 权重衰减:主要用于正则化,防止过拟合
- 动量:主要用于加速收敛,提高训练效率
应用阶段不同:
- 权重衰减:直接影响权重大小
- 动量:影响参数更新的方向和步长
联系:
- 两者都是优化算法的重要组成部分
- 两者都需要根据具体任务进行调整
- 在实际应用中通常同时使用
在您的代码中的应用
在您的代码中,这两个参数在不同优化器中的使用方式如下:
1 | # SGD优化器 |
通过合理设置这两个参数,可以显著提高模型的训练效率和泛化能力。
当前模型请求量过大,请求排队约 1 位,请稍候或切换至其他模型问答体验更流畅。图像分割(Image Segmentation)
原文: https://0809zheng.github.io/2020/05/07/semantic-segmentation.html
图像分割 (Image Segmentation)是对图像中的每个像素进行分类,可以细分为:
语义分割 (semantic segmentation):注重类别之间的区分,而不区分同一类别的不同个体; 实例分割 (instance segmentation):注重类别以及同一类别的不同个体之间的区分; 全景分割 (panoptic segmentation):对于可数的对象实例(如行人、汽车)做实例分割,对于不可数的语义区域(如天空、地面)做语义分割。
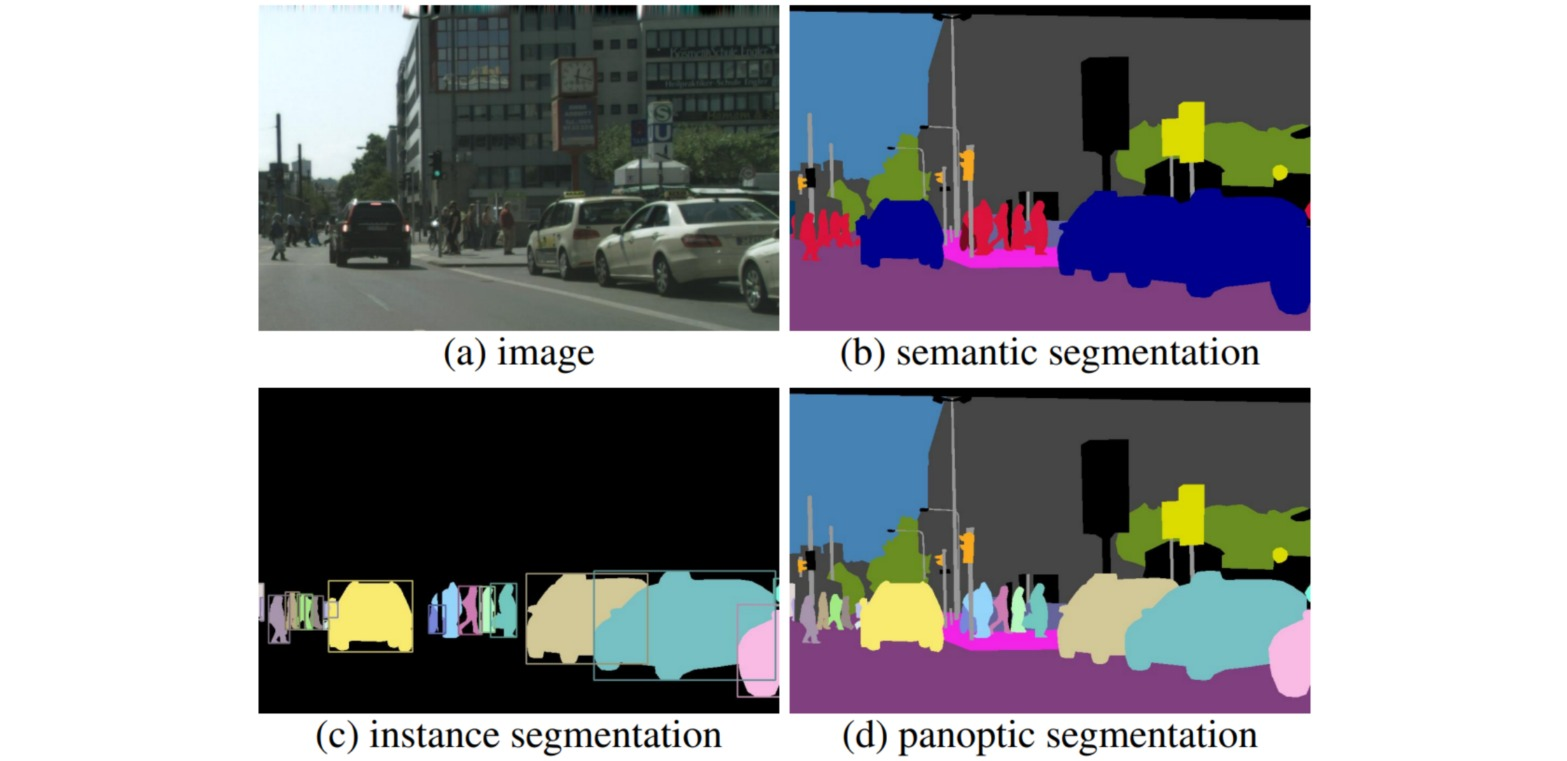
语义分割模型可以直接根据图像像素进行分组,转换为密集的分类问题。实例分割一般可分为“自上而下” 和 “自下而上”的方法,自上而下的框架是先计算实例的检测框,在检测框内进行分割;自下而上的框架则是先进行语义分割,在分割结果上对实例对象进行检测。全景分割在实例分割框架上添加语义分割分支,或基于语义分割方法采用不同的像素分组策略。本文重点关注语义分割方法。
本文目录:
图像分割模型 图像分割的评估指标 图像分割的损失函数 常用的图像分割数据集
1、 图像分割模型
图像分割的任务是使用深度学习模型处理输入图像,得到带有语义标签的相同尺寸的输出图像。

图像分割模型通常采用编码器-解码器(encoder-decoder)结构。编码器从预处理的图像数据中提取特征,解码器把特征解码为分割热图。图像分割模型的发展趋势可以大致总结为:
- 全卷积网络:FCN, SegNet, RefineNet, U-Net, V-Net, M-Net, W-Net, Y-Net, UNet++, Attention U-Net, GRUU-Net, BiSeNet V1,2, DFANet, SegNeXt
- 上下文模块:DeepLab v1,2,3,3+, PSPNet, FPN, UPerNet, EncNet, PSANet, APCNet, DMNet, OCRNet, PointRend, K-Net
- 基于Transformer:SETR, TransUNet, SegFormer, Segmenter, MaskFormer, SAM
- 通用技巧:Deep Supervision, Self-Correction
(1) 基于全卷积网络的图像分割模型
标准卷积神经网络包括卷积层、下采样层和全连接层。早期基于深度学习的图像分割模型为生成与输入图像尺寸一致的分割结果,丢弃了全连接层,并引入一系列上采样操作。因此这一阶段的模型旨在解决如何更好从卷积下采样中恢复丢掉的信息损失,逐渐形成了以U-Net为核心的对称编码器-解码器结构。
FCN
FCN提出用全卷积网络来处理语义分割问题。首先通过全卷积网络进行特征提取和下采样,然后通过双线性插值进行上采样。
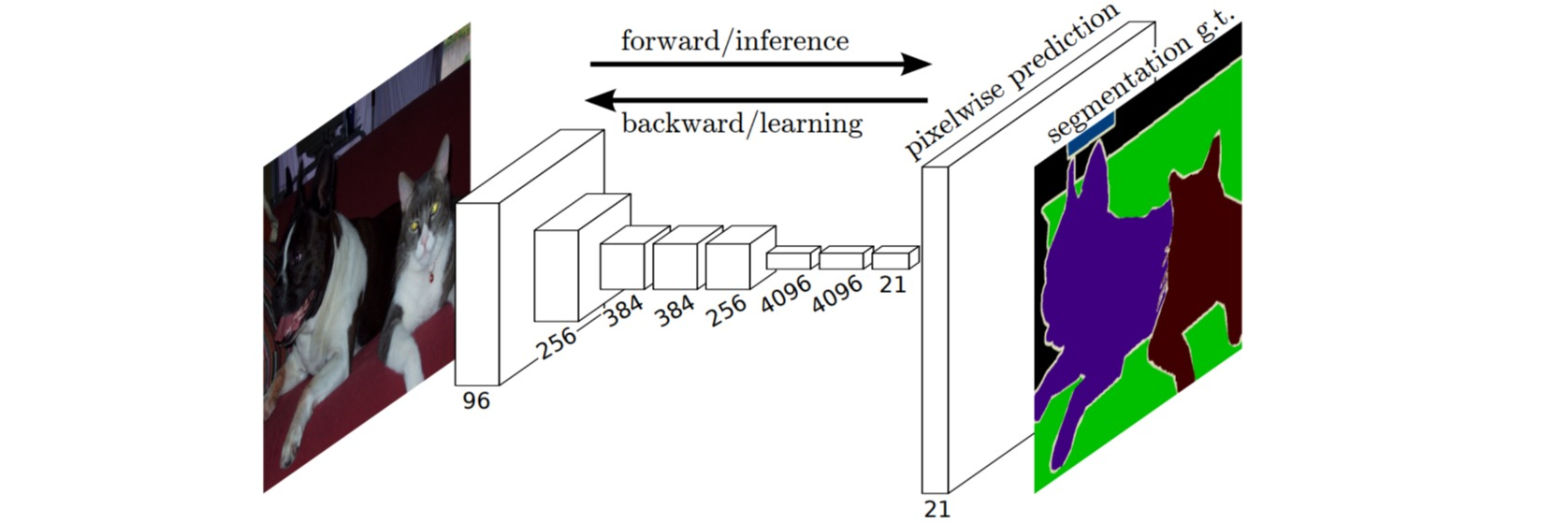
SegNet
SegNet设计了对称的编码器-解码器结构,通过反池化进行上采样。
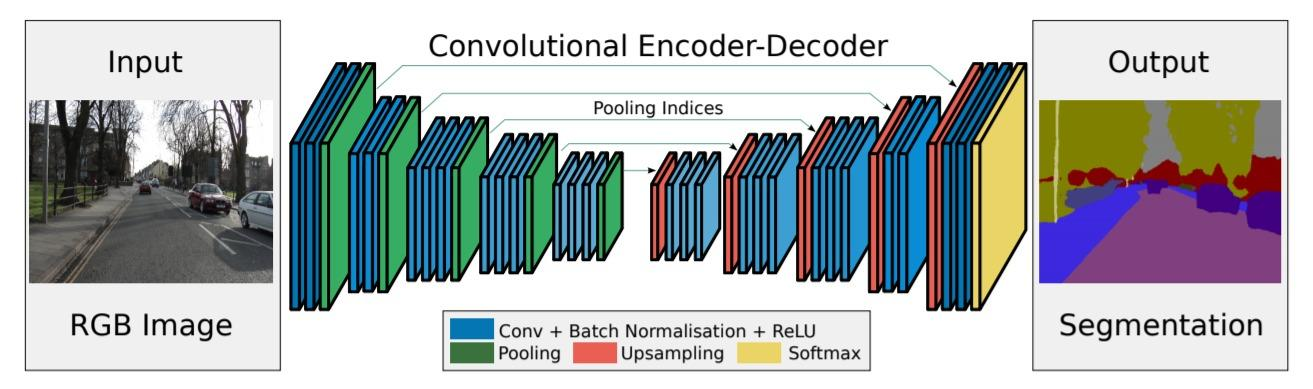
RefineNet
RefineNet把编码器产生的多个分辨率特征进行一系列卷积、融合、池化。
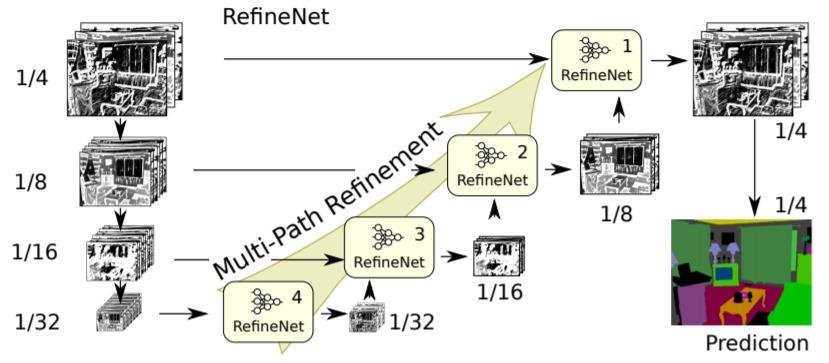 U-Net使用对称的U型网络设计,在对应的下采样和上采样之间引入跳跃连接。
U-Net使用对称的U型网络设计,在对应的下采样和上采样之间引入跳跃连接。
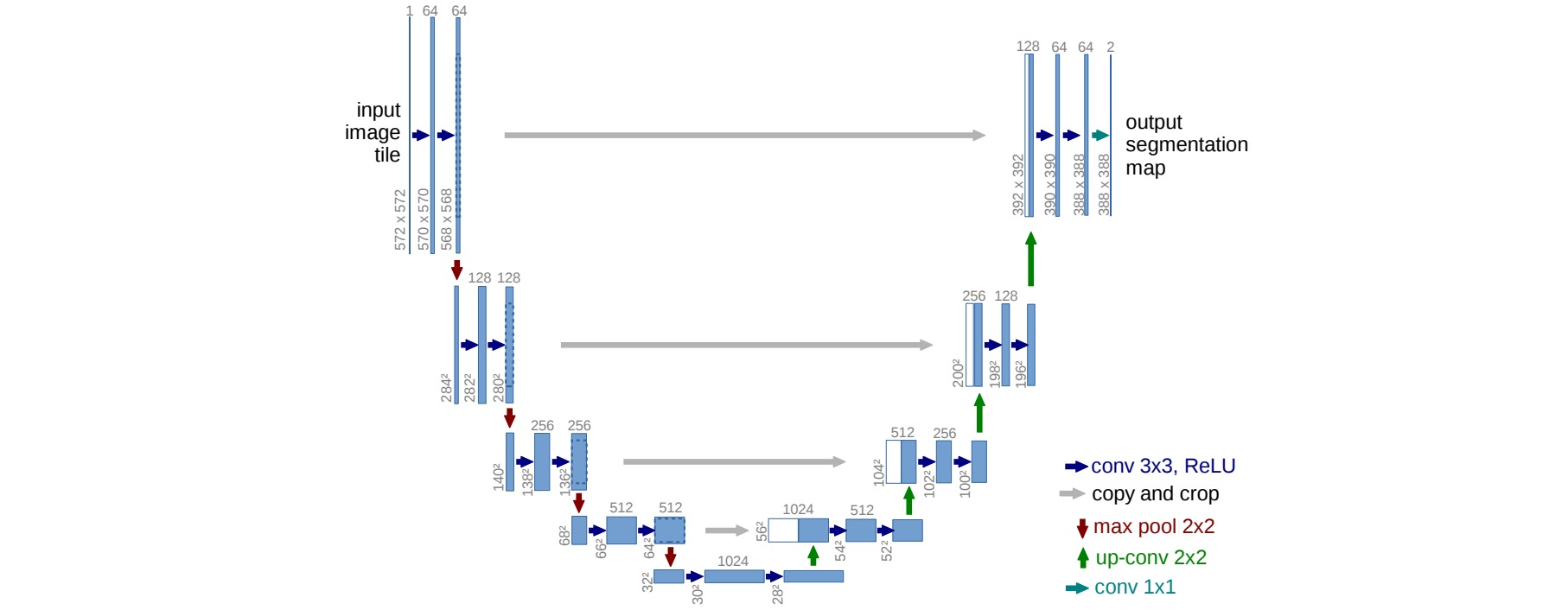
⚪ V-Net V-Net是3D版本的U-Net,下采样使用步长为2的卷积。 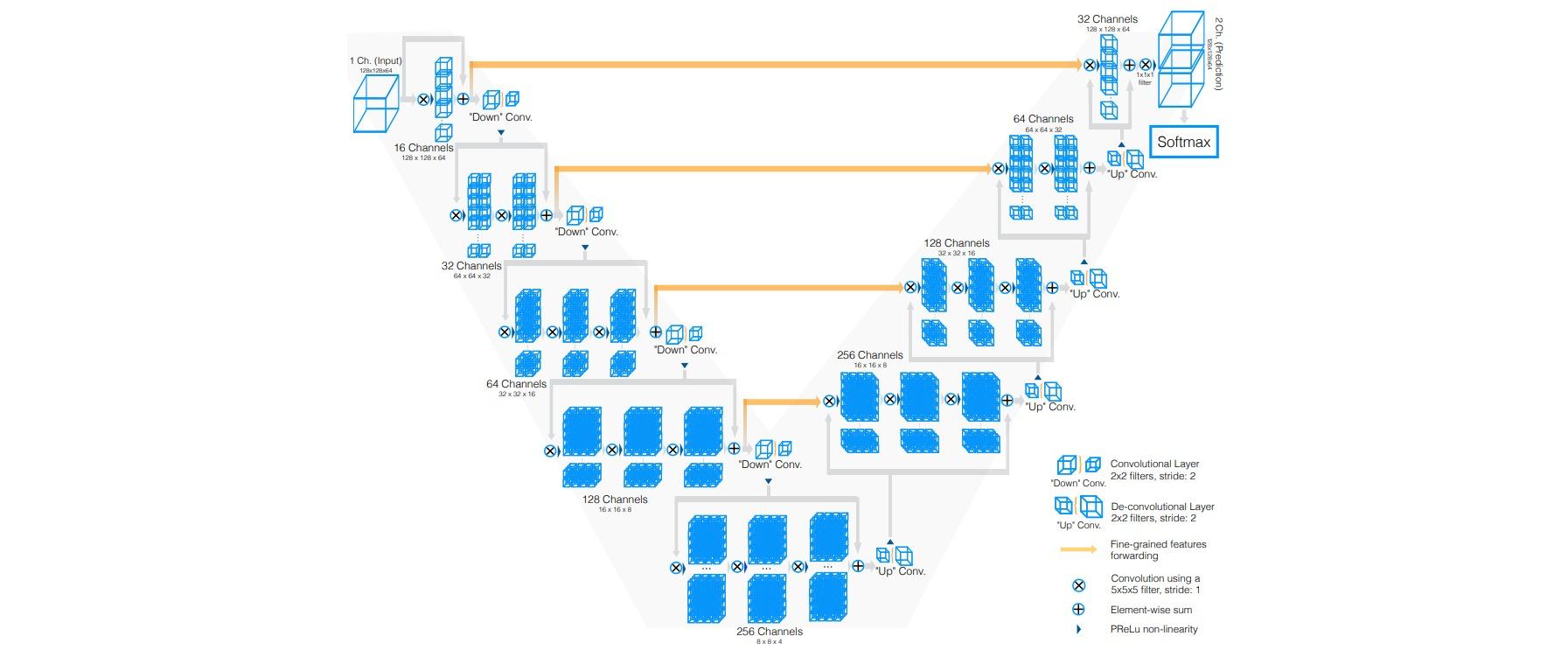
⚪ M-Net M-Net在U-Net的基础上引入了left leg和right leg。left leg使用最大池化不断下采样数据,right leg则对数据进行上采样并叠加到每一层次的输出后。
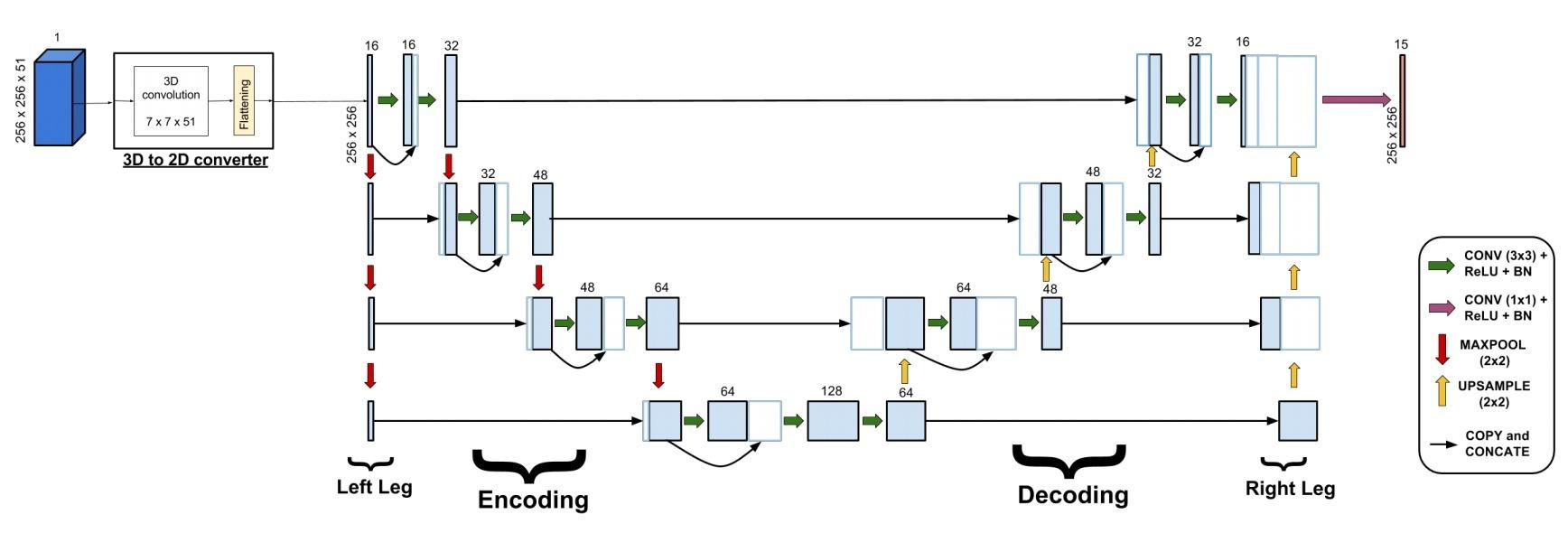
⚪ W-Net
W-Net通过堆叠两个U-Net实现无监督的图像分割。编码器U-Net提取分割表示,解码器U-Net重构原始图像。
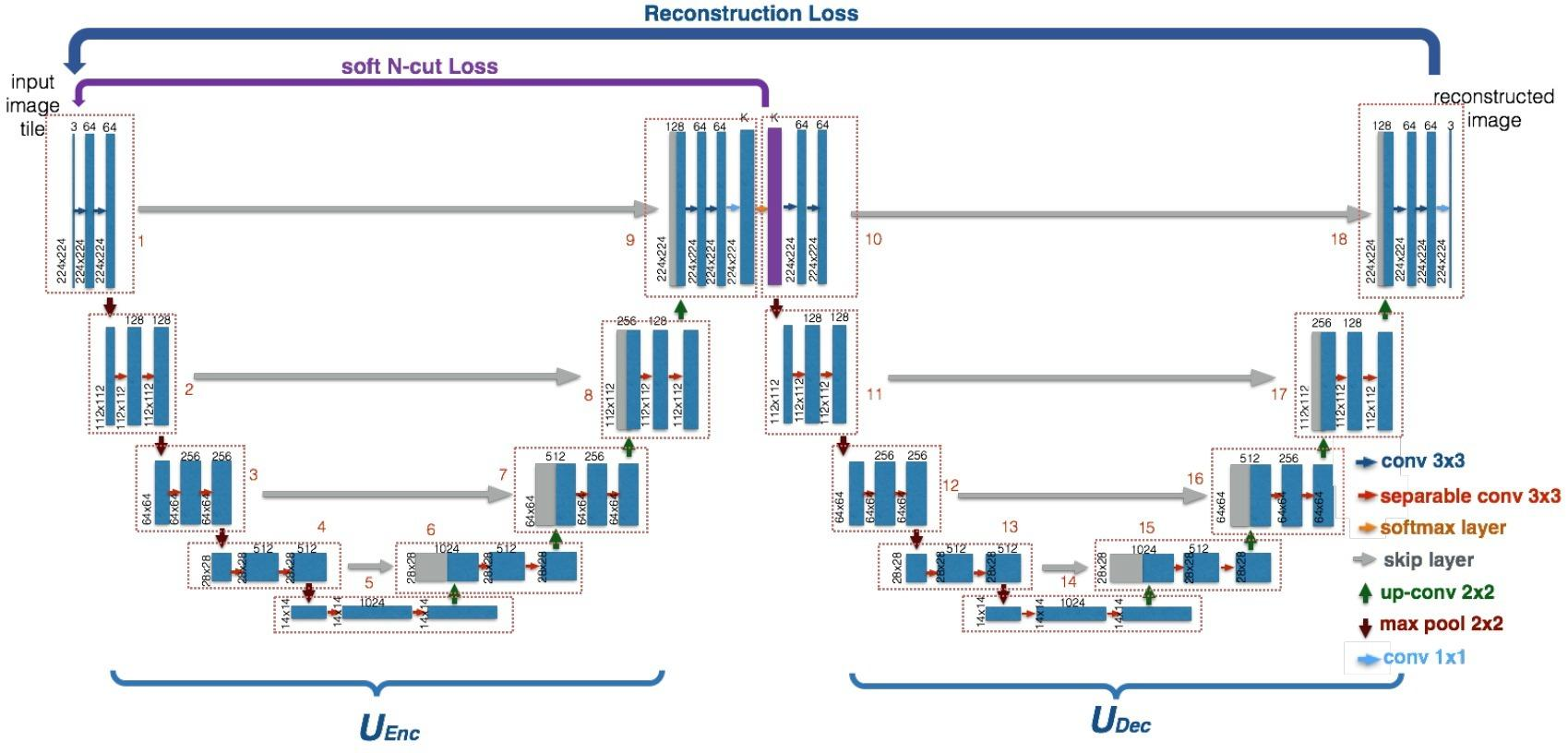
⚪ Y-Net Y-Net在U-Net的编码位置后增加了一个概率图预测结构,在分割任务的基础上额外引入了分类任务。
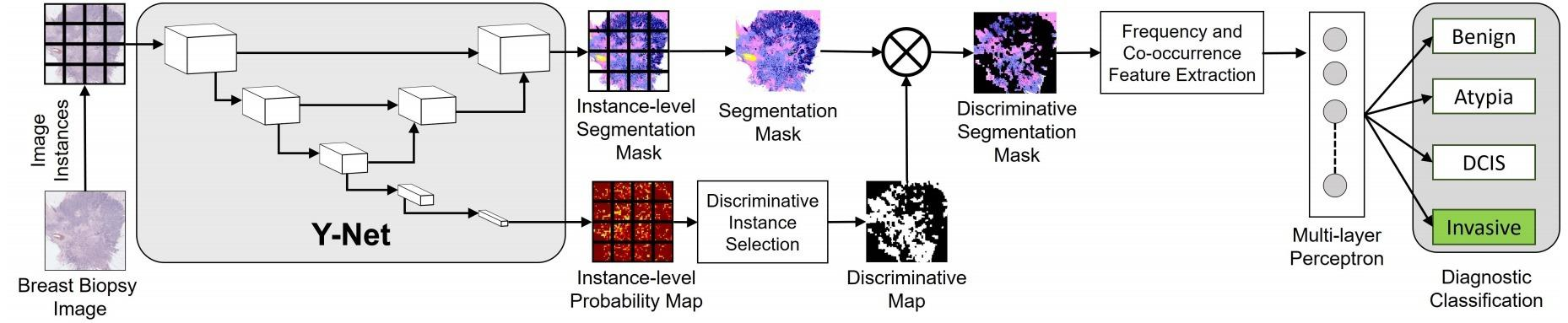
⚪ UNet++
UNet++通过跳跃连接融合了不同深度的U-Net,并为每级U-Net引入深度监督。
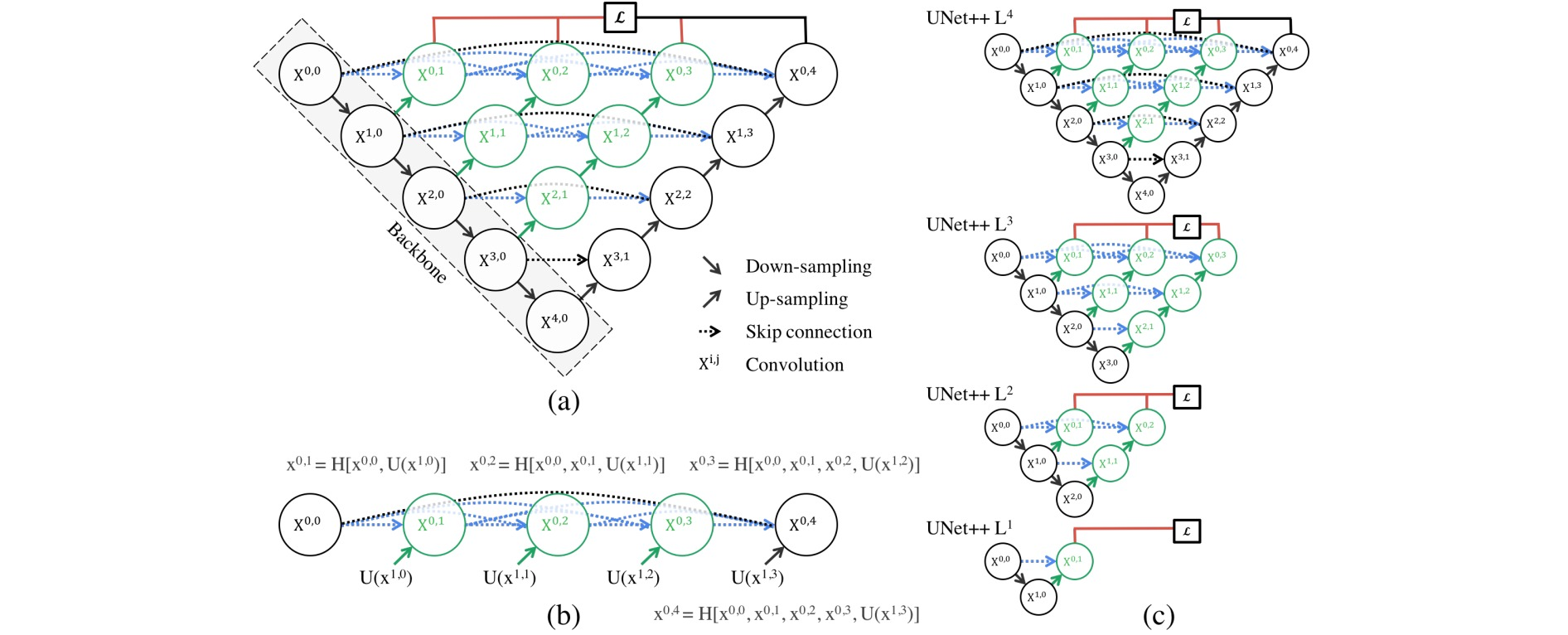
⚪ Attention U-Net Attention U-Net通过引入Attention
gate模块将空间注意力机制集成到U-Net的跳跃连接和上采样模块中。 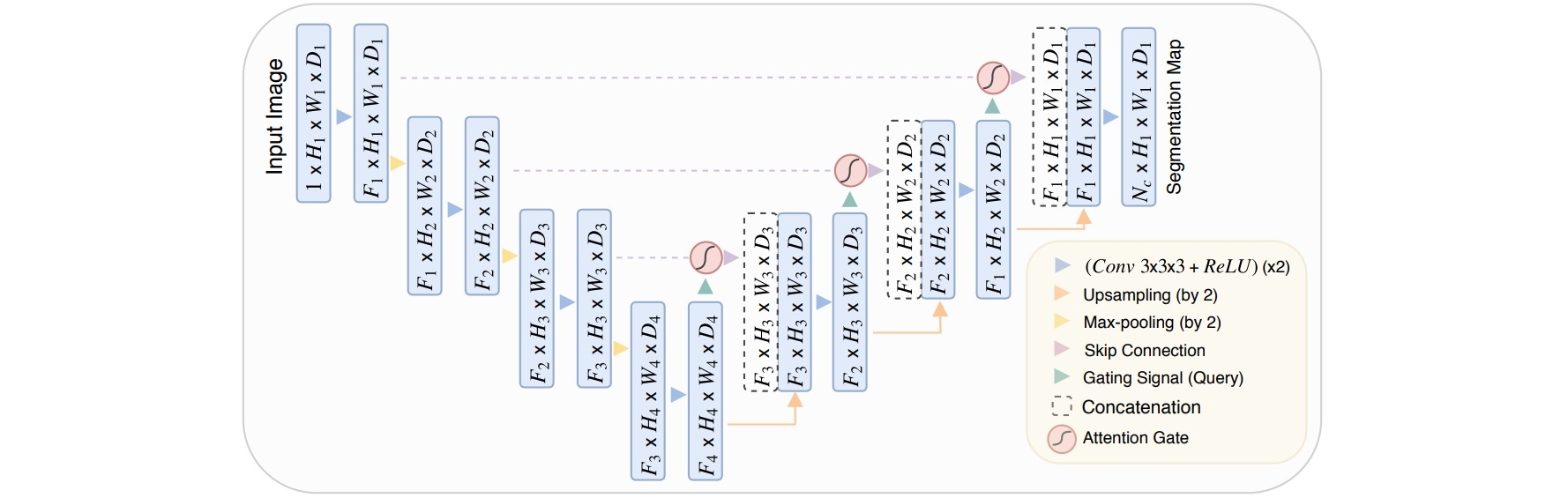
⚪ GRUU-Net
GRUU-Net通过循环神经网络构造U型网络,根据多个尺度上的CNN和RNN特征聚合来细化分割结果。
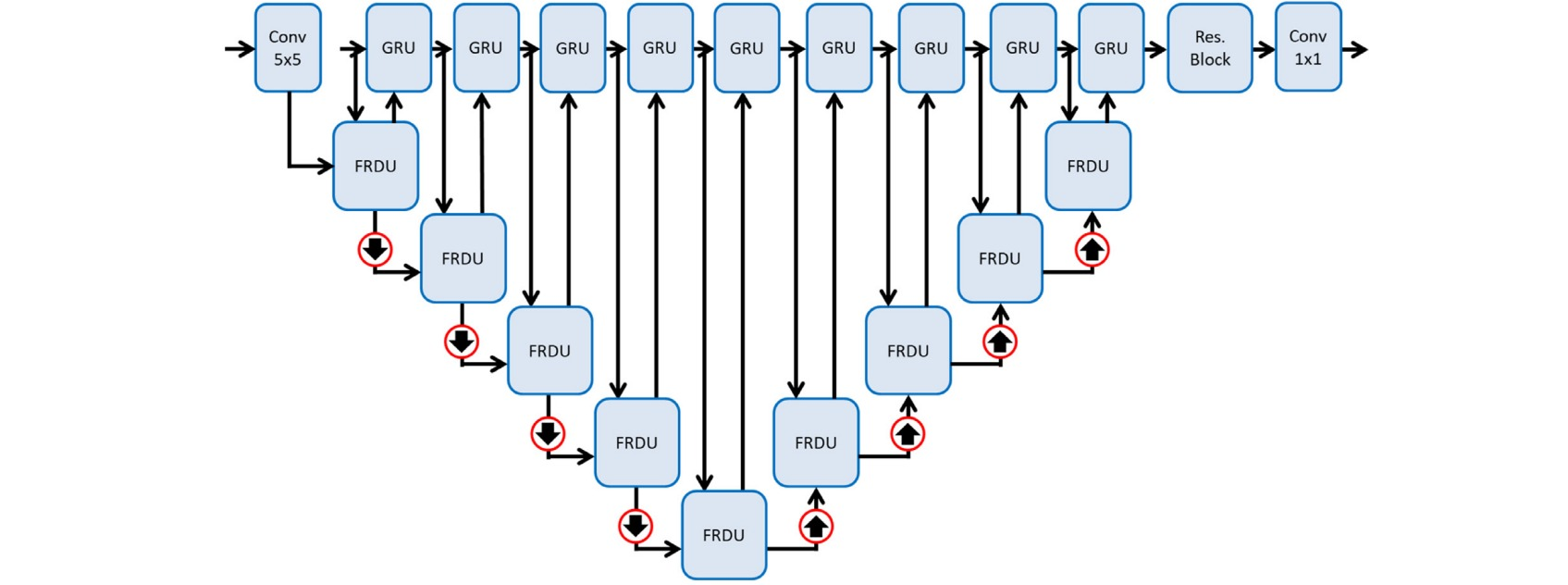
⚪ BiSeNet BiSeNet设计了一个双边结构,分别为空间路径(Spatial Path)和上下文路径(Context Path)。通过一个特征融合模块(FFM)将两个路径的特征进行融合,可以实现实时语义分割。
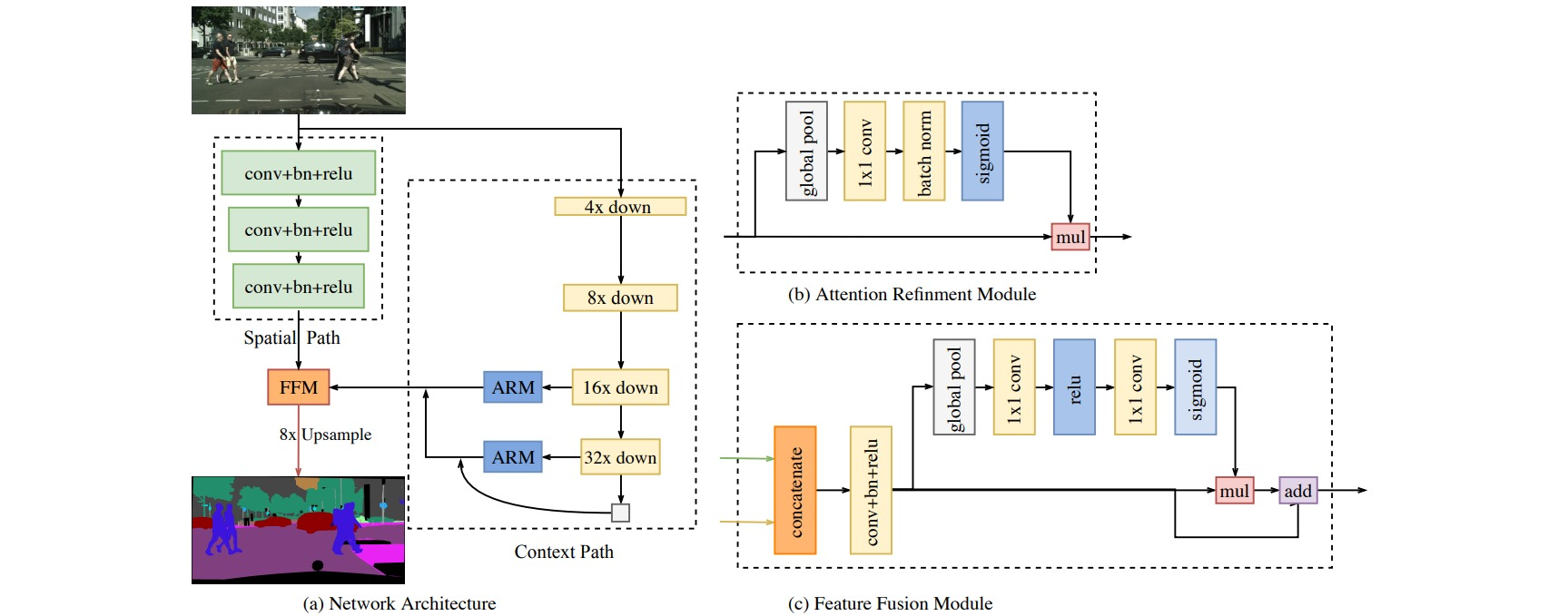
⚪ BiSeNet V2 BiSeNet V2精心设计了Detail Branch和Semantic Branch,使用更加轻巧的深度可分离卷积来加速模型;通过Aggregation Layer进行特征聚合;并额外引入辅助损失。
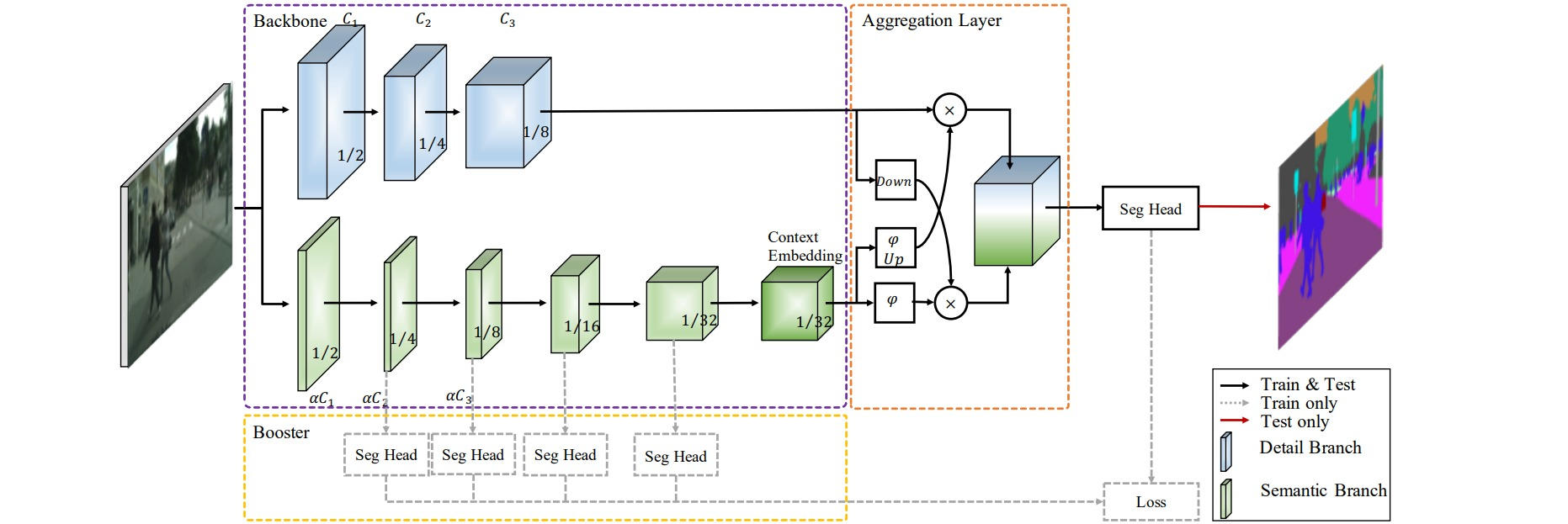
⚪ DFANet
DFANet以修改过的Xception为backbone网络,设计了一种多分支的特征重用框架来融合空间细节和上下文信息。
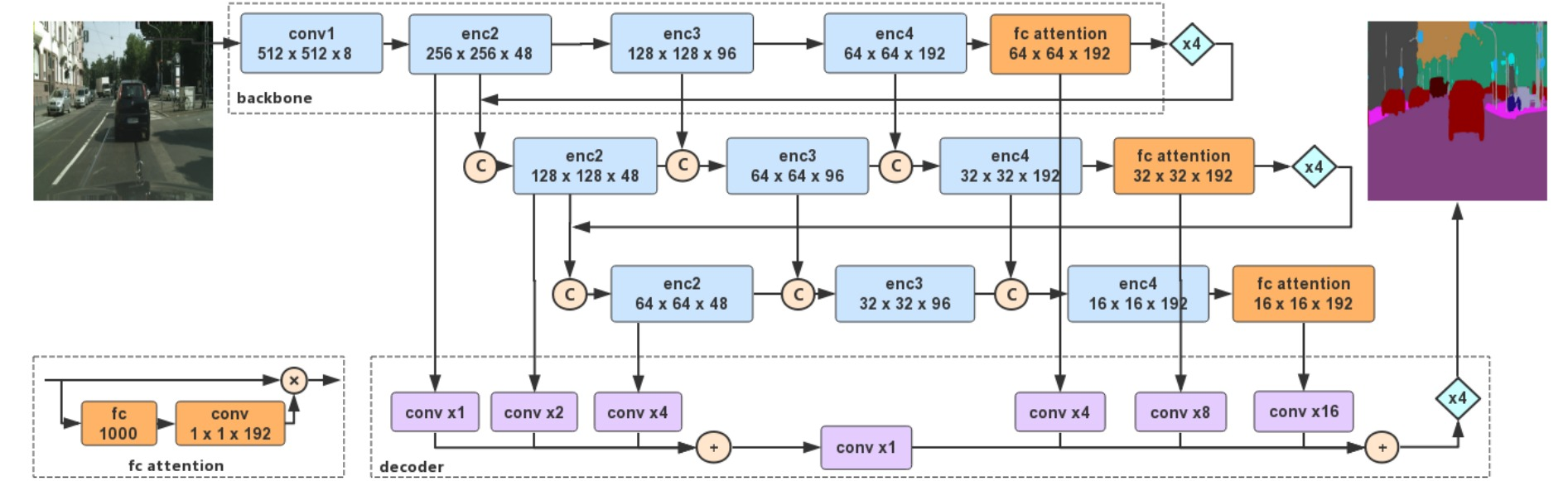
⚪ SegNeXt
SegNeXt的编码器部分采用ViT的结构,自注意力模块通过一种多尺度卷积注意力模块MSCA实现。解码器部分采用轻量型Hamberger模块对后三个阶段的特性进行聚合。
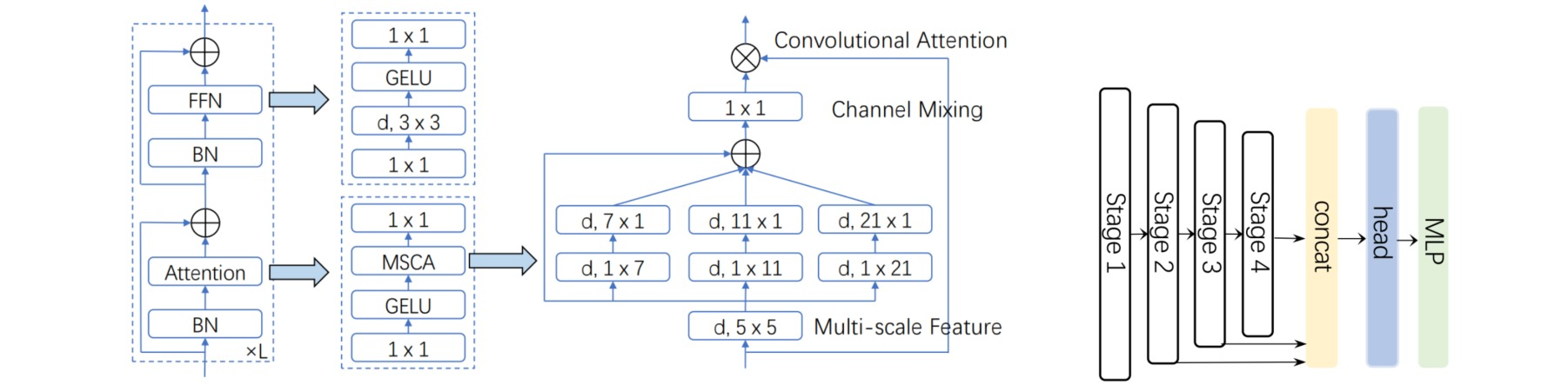
- 基于上下文模块的图像分割模型 多尺度问题是指当图像中的目标对象存在不同大小时,分割效果不佳的现象。比如同样的物体,在近处拍摄时物体显得大,远处拍摄时显得小。解决多尺度问题的目标就是不论目标对象是大还是小,网络都能将其分割地很好。
随着图像分割模型的效果不断提升,分割任务的主要矛盾逐渐从恢复像素信息逐渐演变为如何更有效地利用上下文(context)信息,并基于此设计了一系列用于提取多尺度特征的网络结构。
这一时期的分割网络的基本结构为:首先使用预训练模型(如ResNet)提取图像特征(通常8×下采样),然后应用精心设计的上下文模块增强多尺度特征信息,最后对特征应用上采样(通常为8x上采样)和1x1分割头生成分割结果。
有一些方法把自注意力机制引入图像分割任务,通过自注意力机制的全局交互性来捕获视觉场景中的全局依赖,并以此构造上下文模块。对于这些方法的讨论详见卷积神经网络中的自注意力机制。
⚪ Deeplab
Deeplab引入空洞卷积进行图像分割任务,并使用全连接条件随机场精细化分割结果。
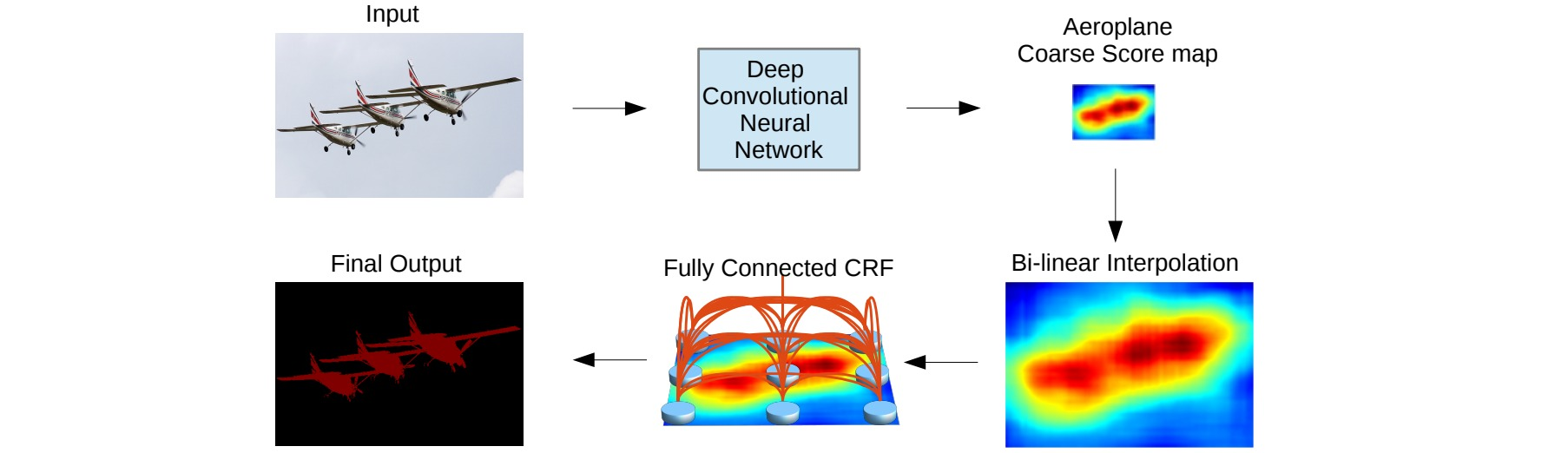
⚪ DeepLab v2 Deeplab v2引入了空洞空间金字塔池化层
ASPP,即带有不同扩张率的空洞卷积的金字塔池化。 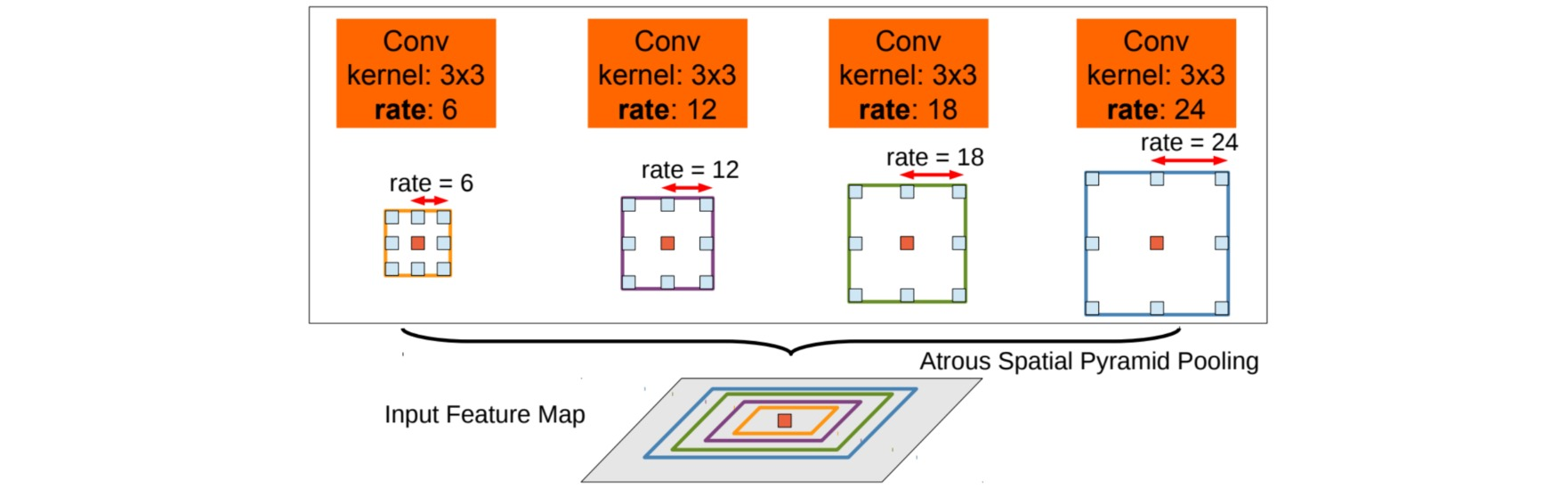
⚪ DeepLab v3 Deeplab v3对ASPP模块做了升级,把扩张率调整为[1, 6, 12,
18],并增加了全局平均池化: 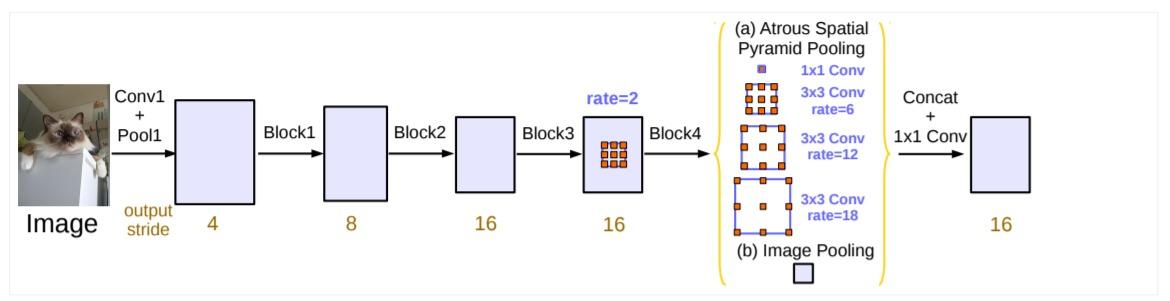
⚪ DeepLab v3+ Deeplab v3+采用了编码器-解码器结构。
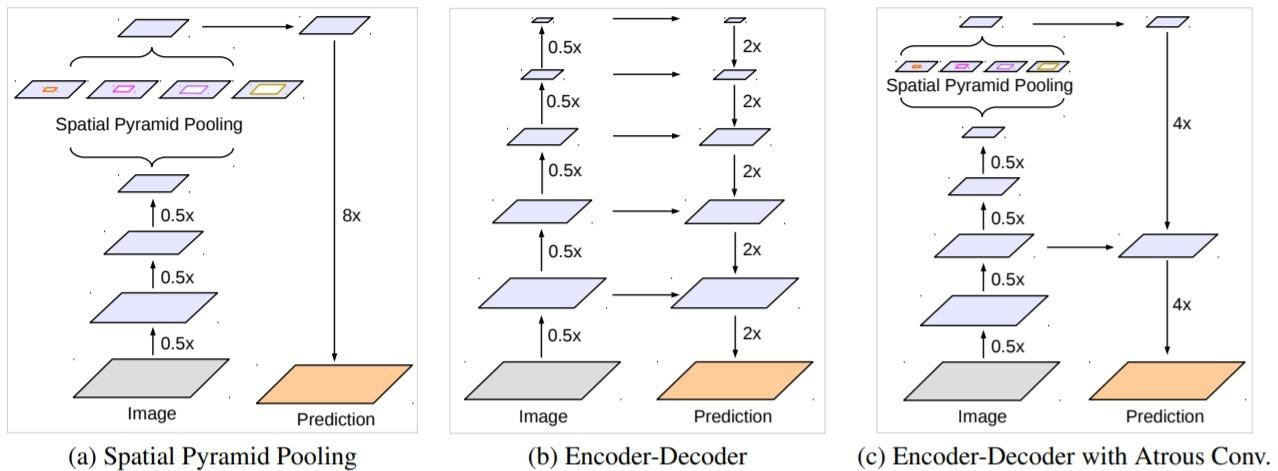
上述Deeplab模型的对比如下:

⚪ PSPNet PSPNet引入了金字塔池化模块 PPM。PPM模块并联了四个不同大小的平均池化层,经过卷积和上采样恢复到原始大小。
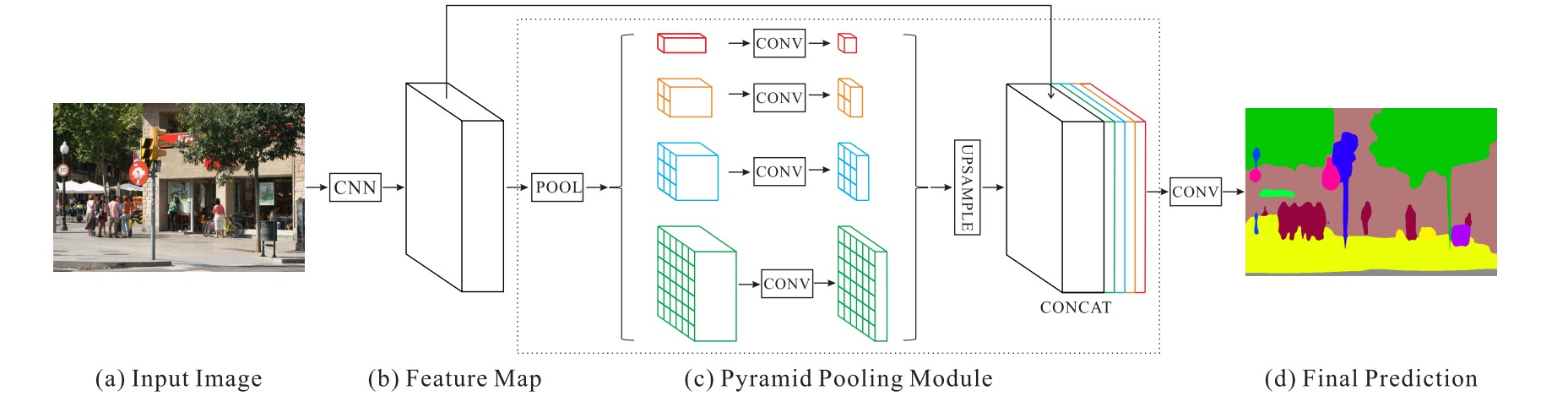
⚪ FPN 特征金字塔网络 FPN金字塔把编码器每一层的特征通过卷积和上采样合并为输出语义特征。
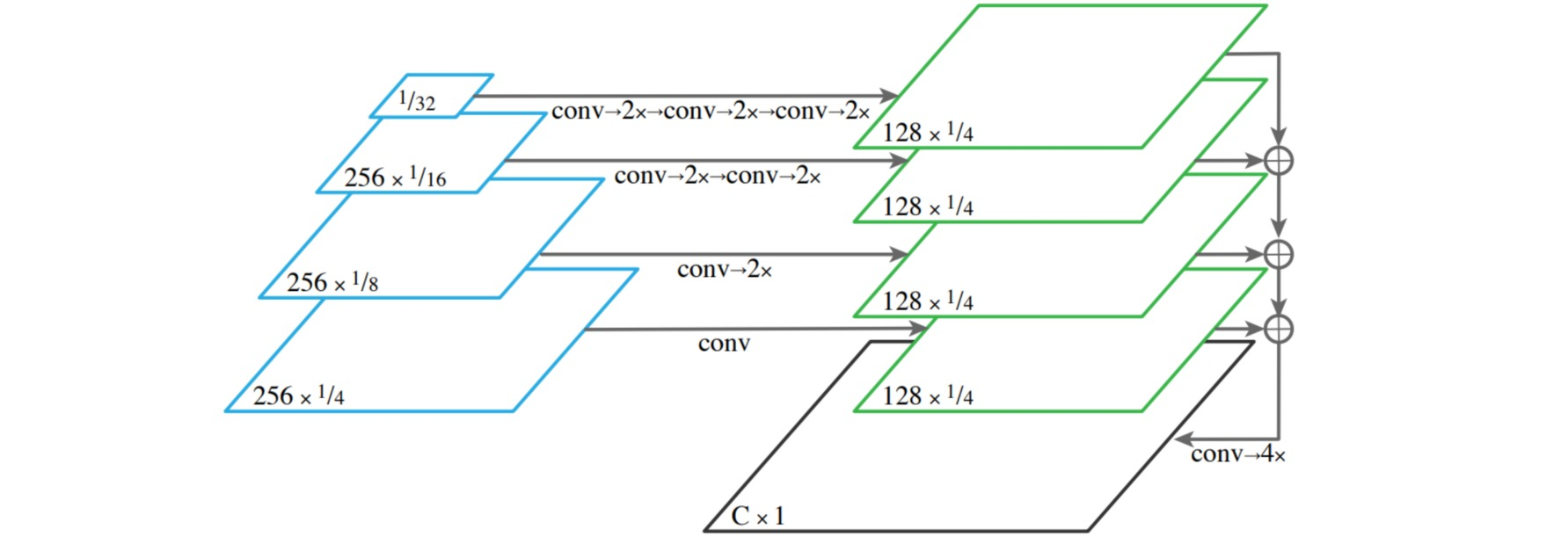
⚪ UPerNet UPerNet设计了一个基于FPN和PPM的多任务分割范式,为每一个task设计了不同的检测头,可执行场景分类、目标和部位分割、材质和纹理检测。
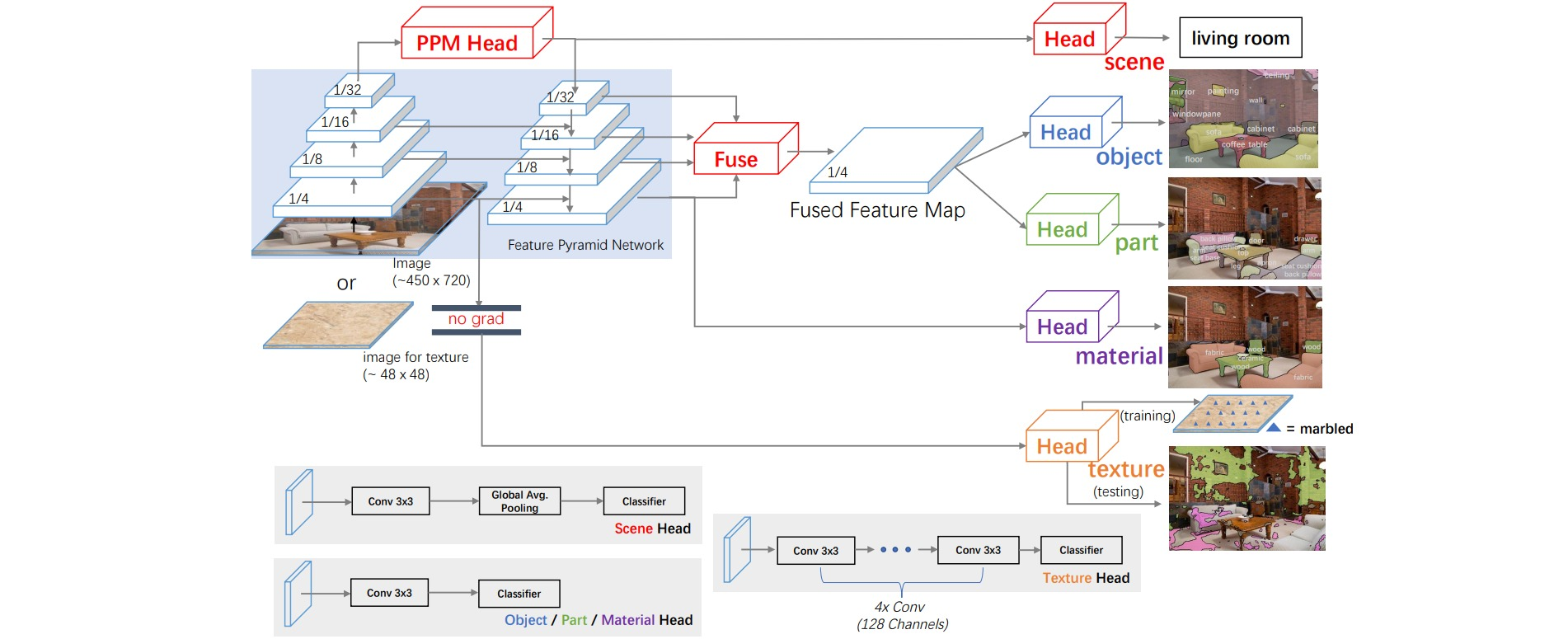
⚪ EncNet EncNet引入了上下文编码模块
CEM,通过字典学习和残差编码捕获全局场景上下文信息;并通过语义编码损失
SE-loss强化网络学习上下文语义。 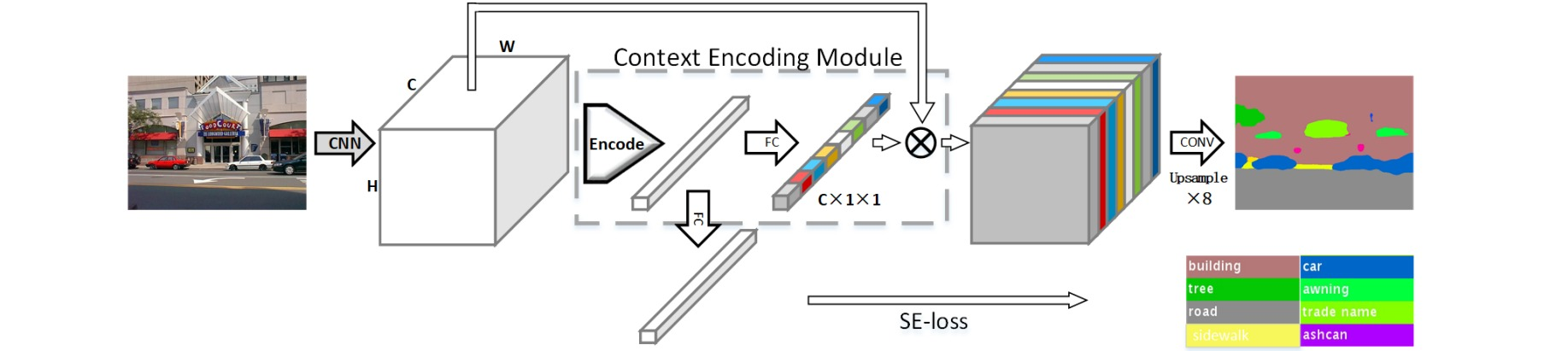
⚪ PSANet PSANet引入了逐点空间注意力
PSA建立每个特征像素与其他像素之间的联系,并且设计了双向的信息流传播路径。
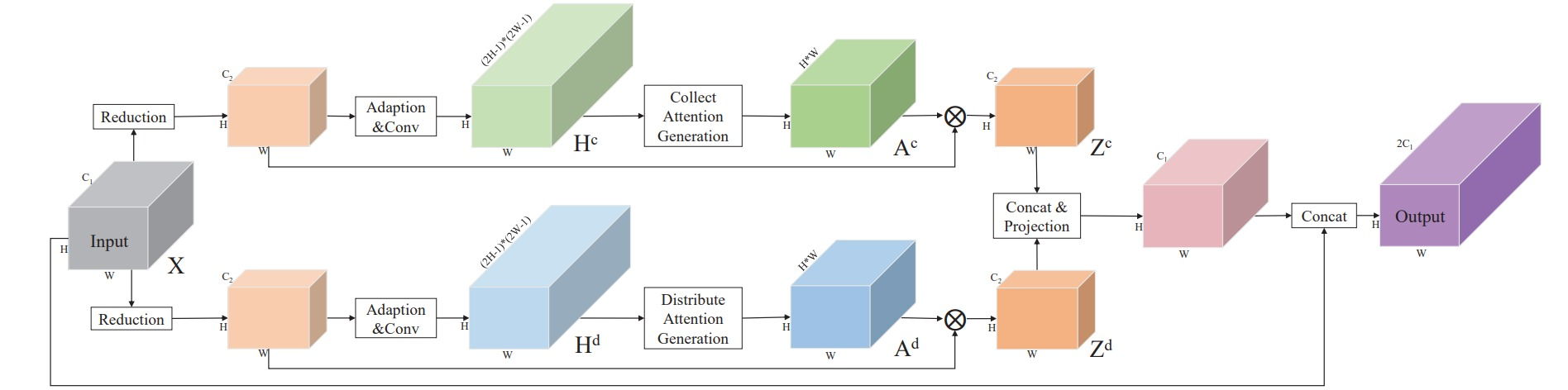
⚪ APCNet APCNet使用了自适应上下文模块ACM计算每个局部位置的上下文向量,并与原始特征图进行加权实现聚合上下文信息的作用。
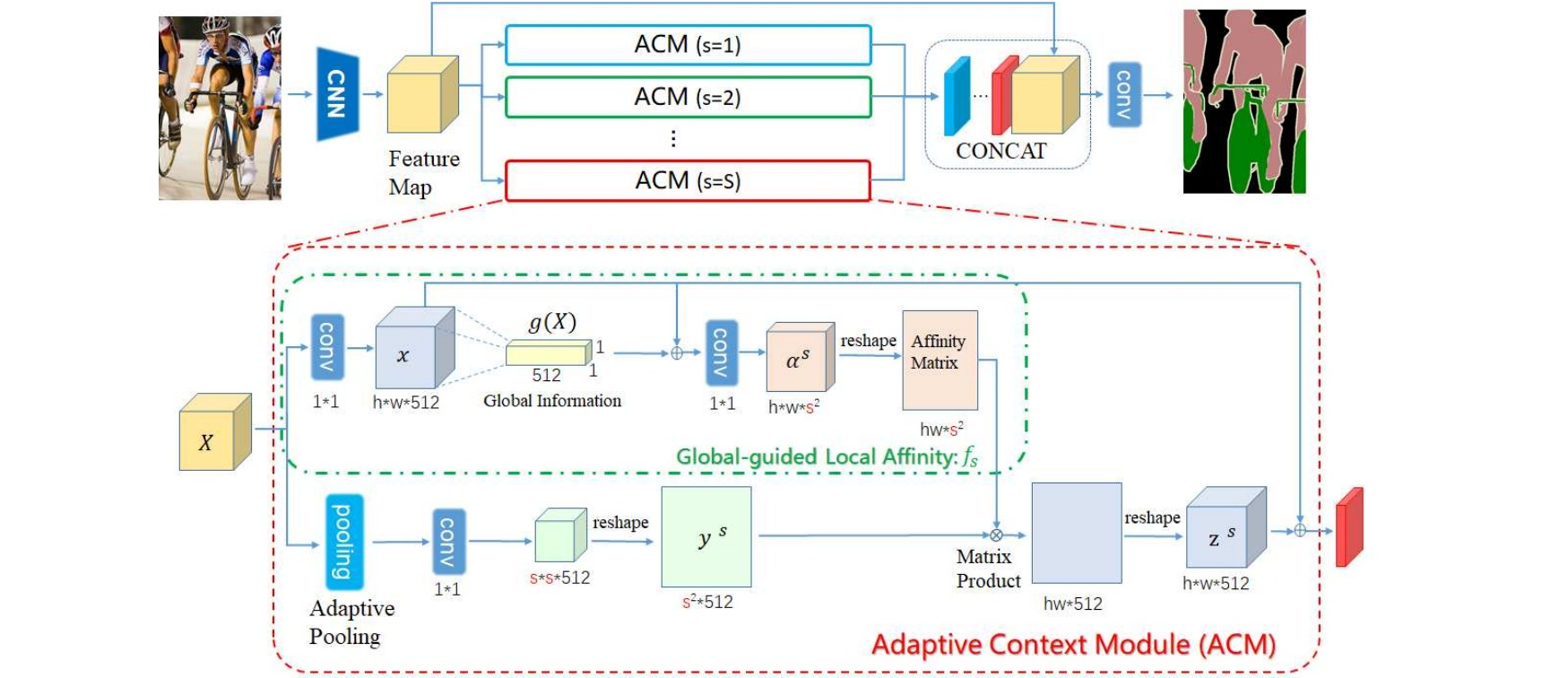
⚪ DMNet DMNet使用了动态卷积模块DCM来捕获多尺度语义信息,每一个DCM模块都可以处理与输入尺寸相关的比例变化。
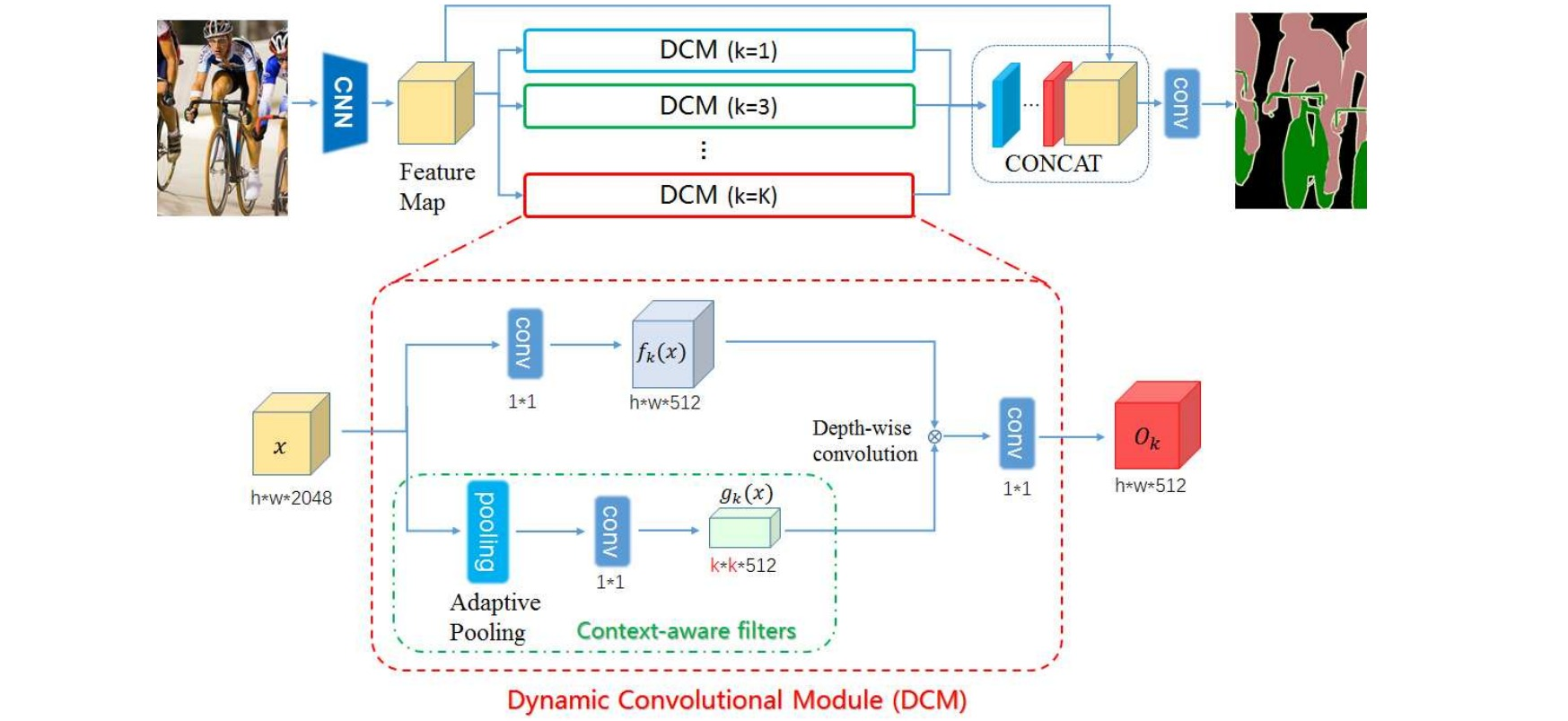
⚪ OCRNet OCRNet根据预测结果和输出像素特征计算类别特征,然后计算像素特征与类别特征的相似度,用于增强特征的上下文表示。

⚪ PointRend PointRend从coarse prediction中挑选N个“难点”,根据其fine-grained features和coarse prediction构造点特征向量,通过MLP网络对这些难点进行重新预测。
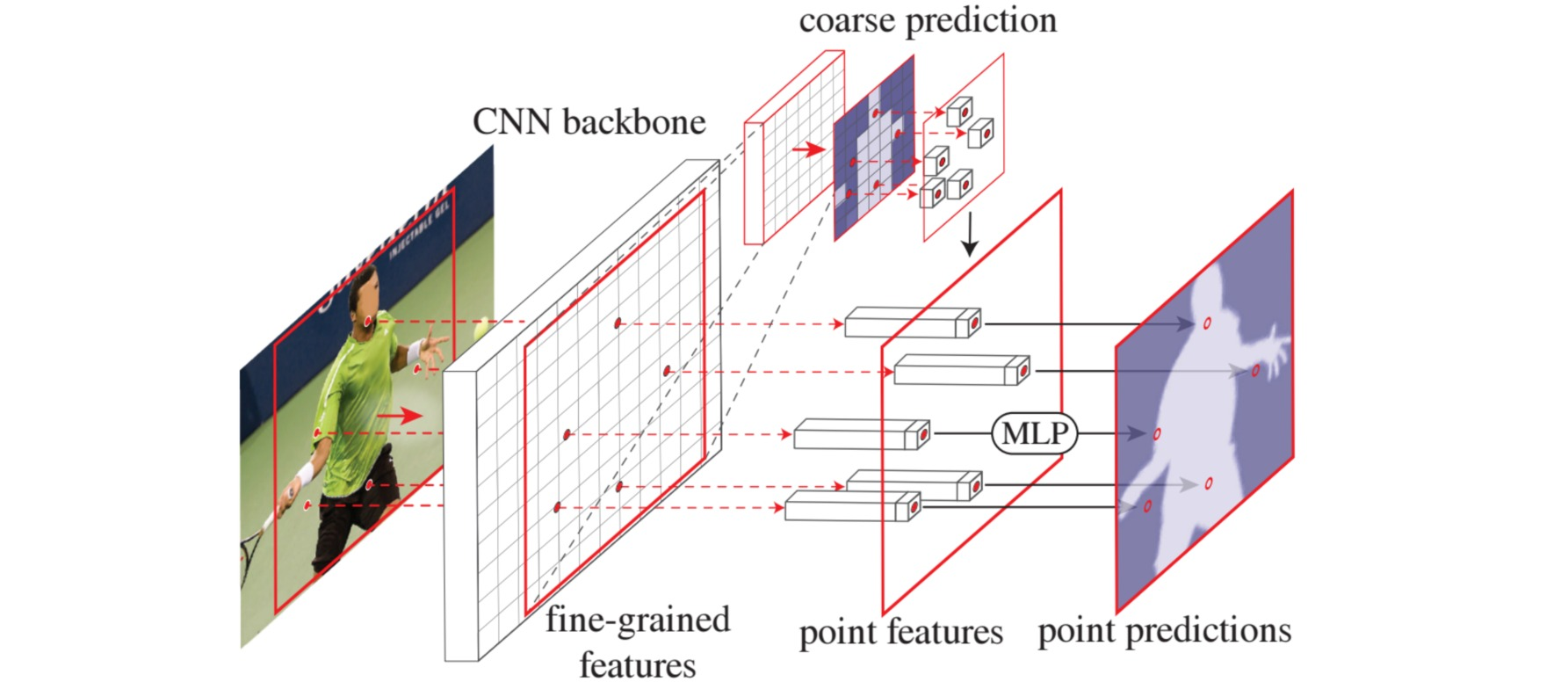
⚪ K-Net
K-Net提出了一种基于动态内核的分割模型,为每个任务分配不同的核来实现语义分割、实例分割和全景分割的统一。具体地,使用N个Kernel将图像划分为N组,每个Kernel都负责找到属于其相应组的像素,并应用Kernel
Update Head增强Kernel的特征提取能力。 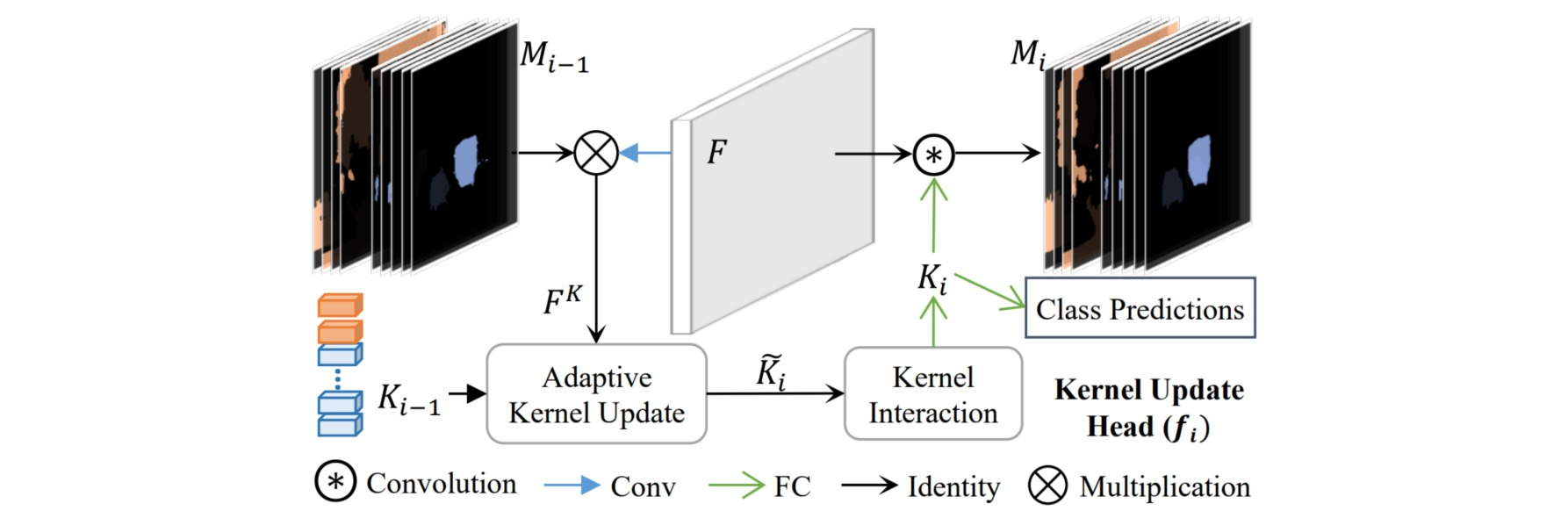
- 基于Transformer的图像分割模型 Transformer是一种基于自注意力机制的序列处理模型,该模型在任意层都能实现全局的感受野,建立全局依赖;而且无需进行较大程度的下采样就能实现特征提取,保留了图像的更多信息。
⚪ SETR SETR采取了ViT作为编码器提取图像特征;通过基于卷积的渐进上采样或者多层次特征聚合生成分割结果。
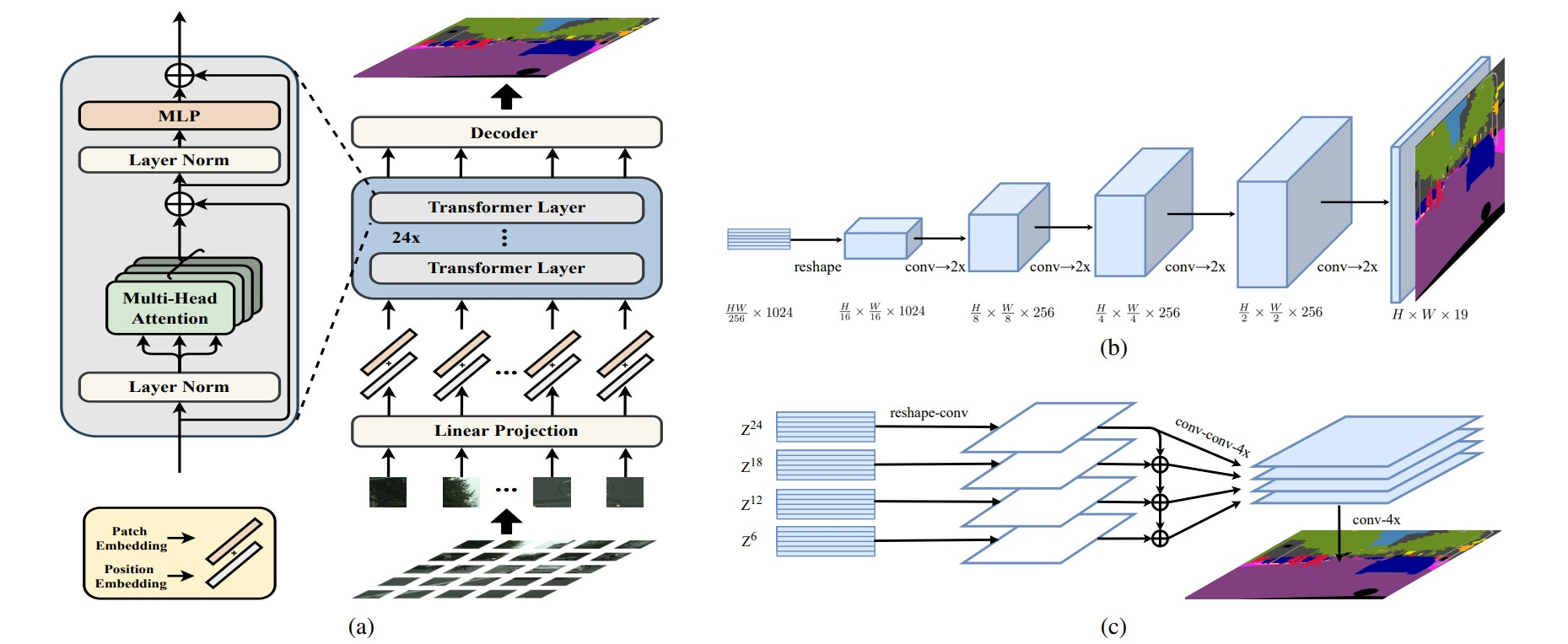
⚪ TransUNet TransUNet的Encoder部分主要由ResNet50和ViT组成,其中前三个模块为两倍下采样的ResNet Block,最后一个模块为12层Transformer Layer。
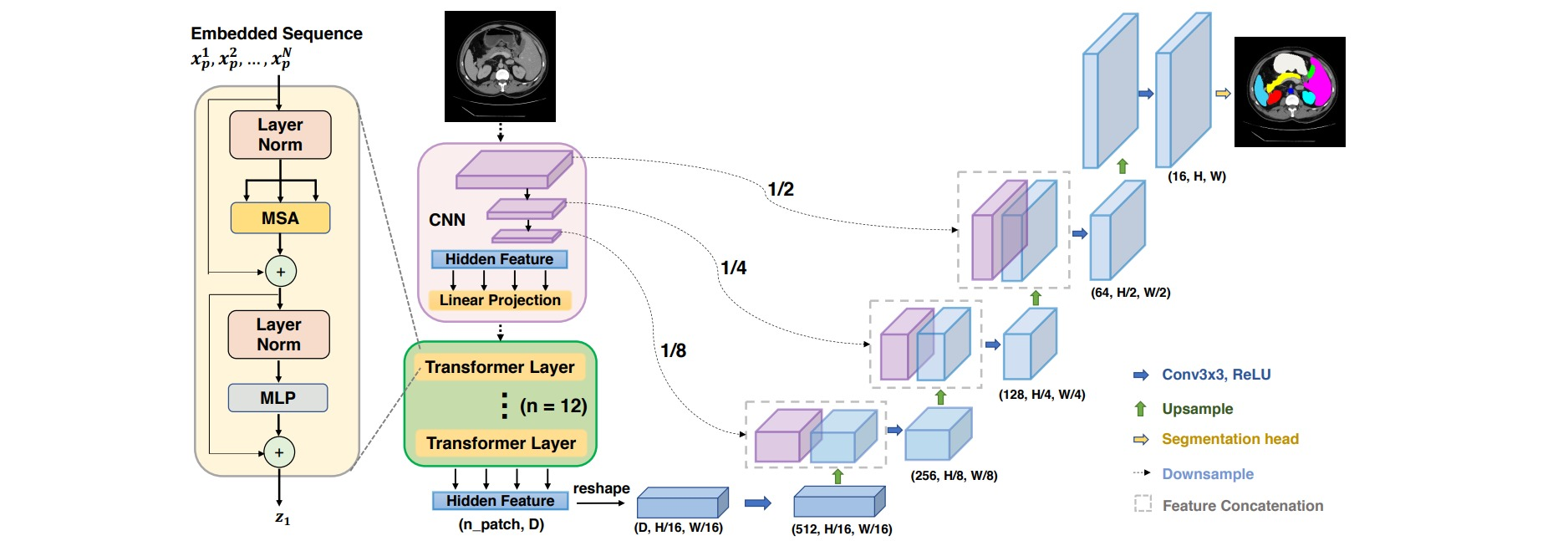
⚪ SegFormer SegFormer包括用于生成多尺度特征的分层Encoder(包含Efficient Self-Attention、Mix-FFN和Overlap Patch Embedding三个模块)和仅由MLP层组成的轻量级All-MLP Decoder。
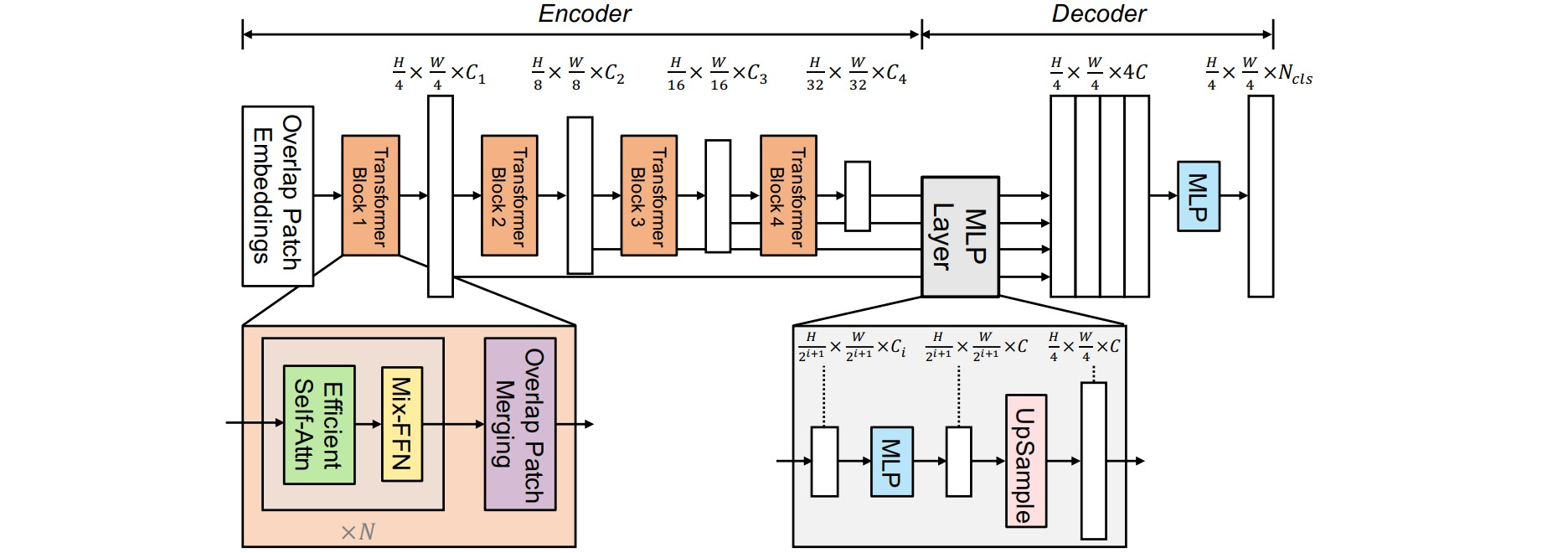
⚪ Segmenter Segmenter完全基于Transformer的编码器-解码器架构。图像块序列由Transformer编码器编码,并由mask Transformer解码。Mask Transformer引入一组个可学习的类别嵌入,通过计算其与解码序列特征的乘积来生成每个图像块的分割图。
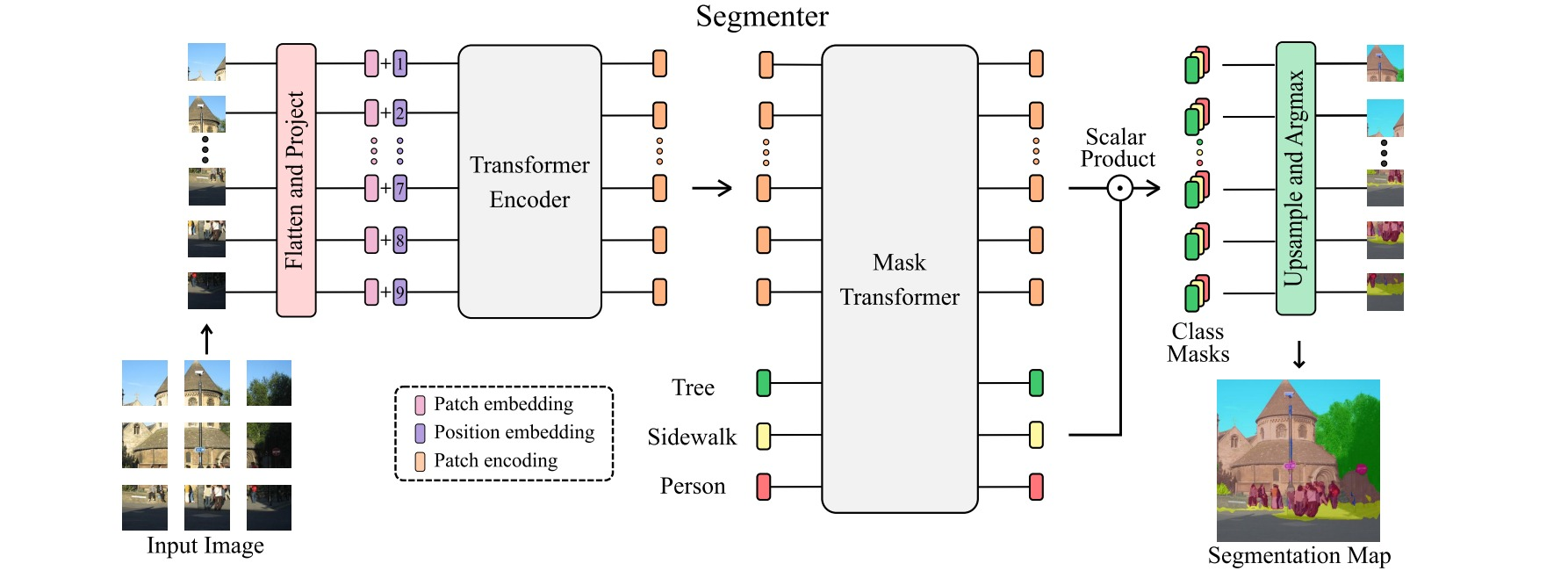
⚪ MaskFormer MaskFormer把分割问题看作掩码级的分类问题。对输入图像生成\(N\)个二值掩码,并为每个掩码预测\(K+1\)个类别中的某个。
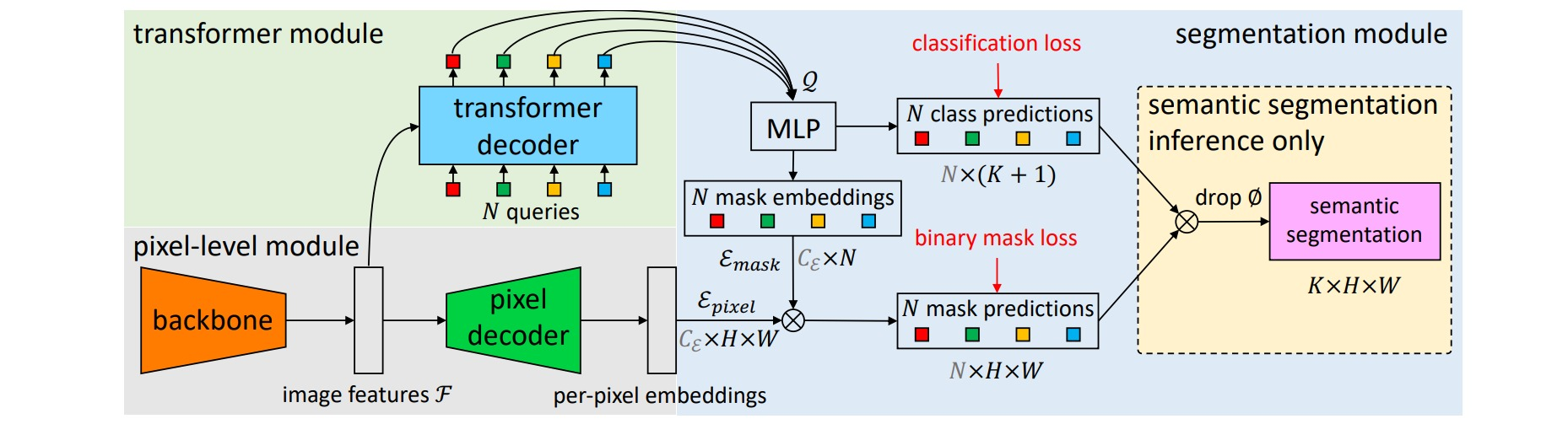
⚪ Segment Anything SAM是一个图像分割的基础模型,模型的设计和训练是通过提示工程实现的。SAM采用一种简单的设计:一个图像编码器生成图像嵌入,一个提示编码器生成提示嵌入,然后将这两种嵌入组合后通过一个轻量级掩码解码器预测分割掩码。

- 分割模型中的通用技巧 ⚪ Deep Supervision Reference:Deeply-Supervised Nets、Training Deeper Convolutional Networks with Deep Supervision 深度监督(Deep Supervision)是在深度神经网络的某些隐藏层后增加一个辅助的分类器作为一种网络分支来对主干网络进行监督的技巧,用来解决深度神经网络训练梯度消失和收敛速度过慢等问题。
一个带有深度监督的八层卷积网络结构如下图所示。在Conv4之后添加了一个监督分类器作为分支。Conv4输出的特征图除了随着主网络进入Conv5之外,也作为输入进入分支分类器。
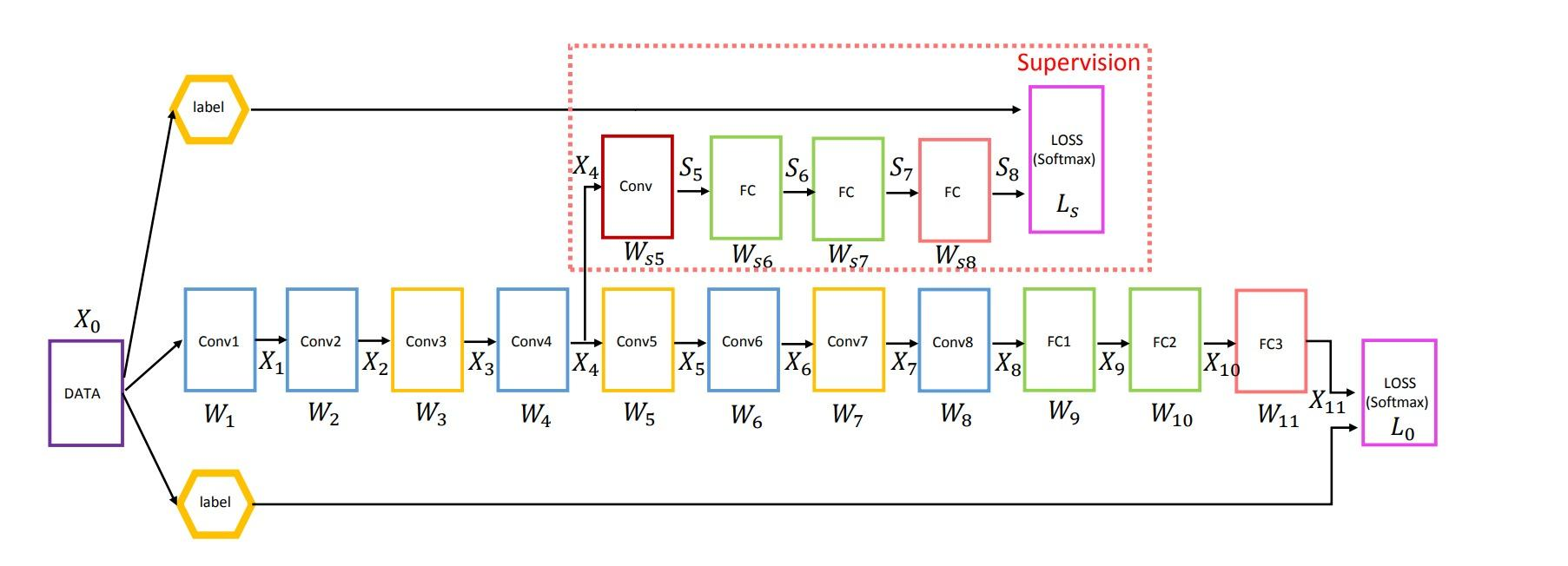
⚪ Self-Correction Reference:Self-Correction for Human Parsing 图像分割任务的标签可能存在噪声。自校正(Self-Correction)是一种净化分割标签噪声的方法。模型训练从具有噪声的标签出发,通过聚合当前模型和前一个最优模型的参数来推断更可靠的标签,并用这些更正的标签训练更鲁棒的模型。
自校正包括模型聚合和标签聚合两个过程。对于模型聚合,记录当前轮数的训练权重 与之前训练的最优权重
与之前训练的最优权重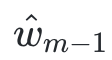 ,得到融合权重并更新历史最优权重:
,得到融合权重并更新历史最优权重:
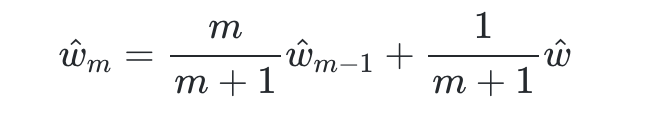 标签的更新类似,通过融合当前预测结果
标签的更新类似,通过融合当前预测结果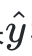 和前一轮标签
和前一轮标签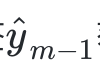 获得类别关系更明确的新标签:
获得类别关系更明确的新标签:
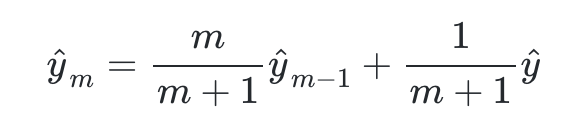
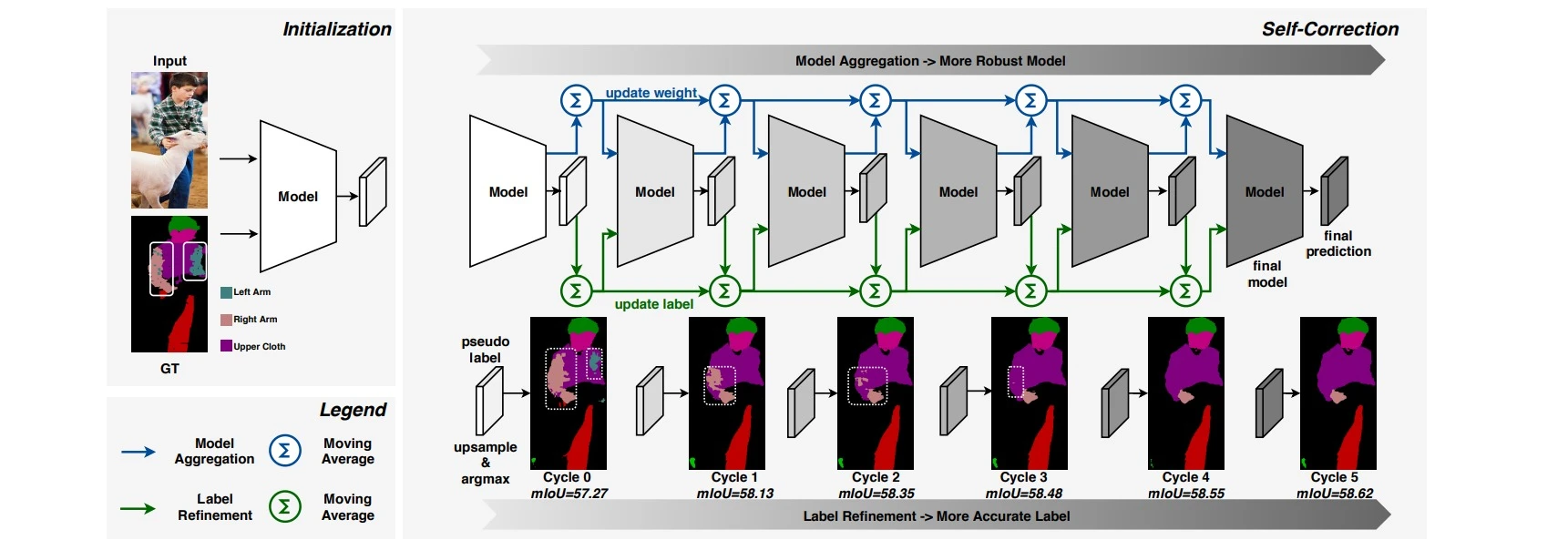
参考文献 Fully Convolutional Networks for Semantic Segmentation:(arXiv1411)FCN: 语义分割的全卷积网络。 Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs:(arXiv1412)DeepLab: 通过深度卷积网络和全连接条件随机场实现图像语义分割。 U-Net: Convolutional Networks for Biomedical Image Segmentation:(arXiv1505)U-Net: 用于医学图像分割的卷积网络。 SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation:(arXiv1511)SegNet: 图像分割的深度卷积编码器-解码器结构。 V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation:(arXiv1606)V-Net:用于三维医学图像分割的全卷积网络。 DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs:(arXiv1606)DeepLab v2: 通过带有空洞卷积的金字塔池化实现图像语义分割。 RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation:(arXiv1611)RefineNet: 高分辨率语义分割的多路径优化网络。 Pyramid Scene Parsing Network:(arXiv1612)PSPNet: 金字塔场景解析网络。 M-Net: A Convolutional Neural Network for Deep Brain Structure Segmentation:(ISBI 2017)M-Net:用于三维脑结构分割的二维卷积神经网络。 Rethinking Atrous Convolution for Semantic Image Segmentation:(arXiv1706)DeepLab v3: 重新评估图像语义分割中的扩张卷积。 W-Net: A Deep Model for Fully Unsupervised Image Segmentation:(arXiv1711)W-Net:一种无监督的图像分割方法。 Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation:(arXiv1802)DeepLab v3+: 图像语义分割中的扩张可分离卷积。 Context Encoding for Semantic Segmentation:(arXiv1803)EncNet: 语义分割的上下文编码。 Attention U-Net: Learning Where to Look for the Pancreas:(arXiv1804)Attention U-Net: 向U-Net引入注意力机制。 Y-Net: Joint Segmentation and Classification for Diagnosis of Breast Biopsy Images:(arXiv1806)Y-Net:乳腺活检图像的分割和分类。 UNet++: A Nested U-Net Architecture for Medical Image Segmentation:(arXiv1807)UNet++:用于医学图像分割的巢型UNet。 Unified Perceptual Parsing for Scene Understanding:(arXiv1807)UPerNet: 场景理解的统一感知解析。 BiSeNet: Bilateral Segmentation Network for Real-time Semantic Segmentation:(arXiv1808)BiSeNet: 实时语义分割的双边分割网络。 PSANet: Point-wise Spatial Attention Network for Scene Parsing:(ECCV2018)PSANet: 场景解析的逐点空间注意力网络。 GRUU-Net: Integrated convolutional and gated recurrent neural network for cell segmentation:(Medical Image Analysis2018)GRUU-Net: 细胞分割的融合卷积门控循环神经网络。 Panoptic Feature Pyramid Networks:(arXiv1901)全景特征金字塔网络。 DFANet: Deep Feature Aggregation for Real-Time Semantic Segmentation:(arXiv1904)DFANet: 实时语义分割的深度特征聚合。 Object-Contextual Representations for Semantic Segmentation:(arXiv1909)OCRNet:语义分割中的目标上下文表示。 PointRend: Image Segmentation as Rendering:(arXiv1912)PointRend: 把图像分割建模为渲染。 Adaptive Pyramid Context Network for Semantic Segmentation:(CVPR2019)APCNet: 语义分割的自适应金字塔上下文网络。 Dynamic Multi-Scale Filters for Semantic Segmentation:(ICCV2019)DMNet: 语义分割的动态多尺度滤波器。 BiSeNet V2: Bilateral Network with Guided Aggregation for Real-time Semantic Segmentation:(arXiv2004)BiSeNet V2: 实时语义分割的带引导聚合的双边网络。 Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers:(arXiv2012)用Transformer从序列到序列的角度重新思考语义分割。 TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation:(arXiv2102)TransUNet:用Transformer为医学图像分割构造强力编码器。 SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers:(arXiv2105)SegFormer:为语义分割设计的简单高效的Transformer模型。 Segmenter: Transformer for Semantic Segmentation:(arXiv2105)Segmenter:为语义分割设计的视觉Transformer。 K-Net: Towards Unified Image Segmentation:(arXiv2106)K-Net: 面向统一的图像分割。 Per-Pixel Classification is Not All You Needfor Semantic Segmentation:(arXiv2107)MaskFormer:逐像素分类并不是语义分割所必需的。 SegNeXt: Rethinking Convolutional Attention Design for Semantic Segmentation:(arXiv2209)SegNeXt:重新思考语义分割中的卷积注意力设计。 Segment Anything:(arXiv2304)SAM:分割任意模型
模型训练过程中常遇到的问题:
一、梯度消失
梯度消失出现的原因: 在深层网络中,如果激活函数的导数小于1,根据链式求导法则,靠近输入层的参数的梯度因为乘了很多的小于1的数而越来越小,最终就会趋近于0,例如sigmoid函数,其导数f′(x)=f(x)(1−f(x))的值域为(0,1/4),极易发生这种情况。 所以梯度消失出现的原因经常是因为网络层次过深,以及激活函数选择不当,比如sigmoid函数。
梯度消失的表现: 模型无法从训练数据中获得更新,损失几乎保持不变。
二、梯度爆炸
梯度爆炸出现的原因: 同梯度消失的原因一样,求解损失函数对参数的偏导数时,在梯度的连续乘法中总是遇上很大的绝对值,部分参数的梯度因为乘了很多较大的数而变得非常大,导致模型无法收敛。 所以梯度爆炸出现的原因也是网络层次过深,或者权值初始化值太大。
梯度爆炸的表现: (1)模型型不稳定,更新过程中的损失出现显著变化。 (2)训练过程中,模型损失变成 NaN。
三、梯度消失爆炸的解决方法:
重新设置网络结构,减少网络层数,调整学习率(消失增大,爆炸减小)。 预训练加微调 此方法来自Hinton在2006年发表的一篇论文,Hinton为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程就是逐层“预训练”(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。Hinton在训练深度信念网络(Deep Belief Networks中,使用了这个方法,在各层预训练完成后,再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。 激活函数采用relu,leaky relu,elu等。 batch normalization 更换参数初始化方法(对于CNN,一般用xavier或者msra的初始化方法) 调整深度神经网络的结构 使用残差模块,DESNET模块或LSTM等结构(避免梯度消失) l1、l2正则化(避免梯度爆炸) 减小学习率、减小batch size(避免梯度爆炸) 梯度裁剪(避免梯度爆炸) 对于RNN,加入gradient clipping,每当梯度达到一定的阈值,就把他们设置回一个小一些的数字;
loss突然变nan的原因?
可能原因: 1、training sample中出现了脏数据,或输入数据未进行归一化 2、学习速率过大,梯度值过大,产生梯度爆炸; 3、在某些涉及指数计算,可能最后算得值为INF(无穷)(比如不做其他处理的softmax中分子分母需要计算exp(x),值过大,最后可能为INF/INF,得到NaN,此时你要确认你使用的softmax中在计算exp(x)做了相关处理(比如减去最大值等等)); 4、不当的损失函数(尤其是自定义的损失函数时); 5、在卷积层的卷积步伐大于卷积核大小的时候。
现在的网络普遍采用ReLU激活函数,为什么仍然存在梯度爆炸和消失的问题呢?
梯度消失和 梯度爆炸在relu下都存在, 随着 网络层数变深, activations倾向于越大和越小的方向前进, 往大走梯度爆炸(回想一下你在求梯度时, 每反向传播一层, 都要乘以这一层的activations), 往小走进入死区, 梯度消失。 这两个问题最大的影响是,深层网络难于converge。BN和xavier初始化(经指正, 这里最好应该用msra初始化, 这是he kaiming大神他们对xavier的修正, 其实就是xavier多除以2)很大程度上解决了该问题。sigmoid不存在梯度爆炸, 在activations往越大越小的方向上前进时, 梯度都会消失。 ReLU的负半轴梯度为0,所以有时候(比较少见)也还是会梯度消失,这时可以使用PReLU替代,如果用了PReLU还会梯度弥散和爆炸,请调整初始化参数,对自己调参没信心或者就是懒的,请直接上BN。至于sigmoid为什么会有梯度消失现象,是因为sigmoid(x)在不同尺度的x下的梯度变化太大了,而且一旦x的尺度变大,梯度消失得特别快,网络得不到更新,就再也拉不回来了。
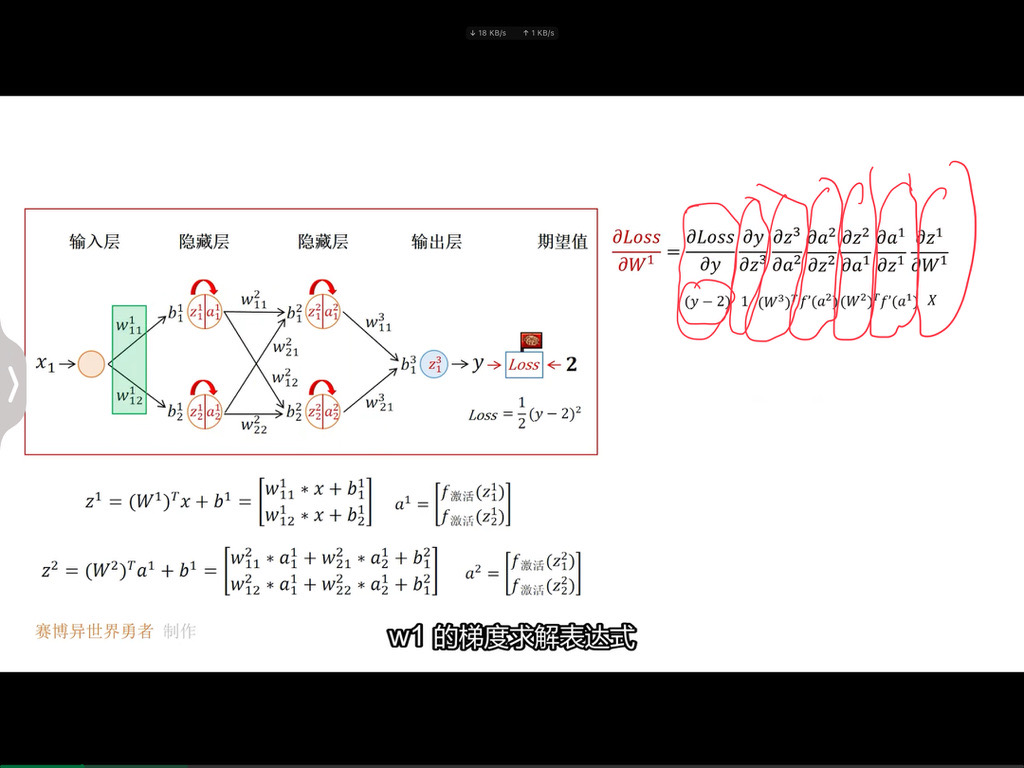
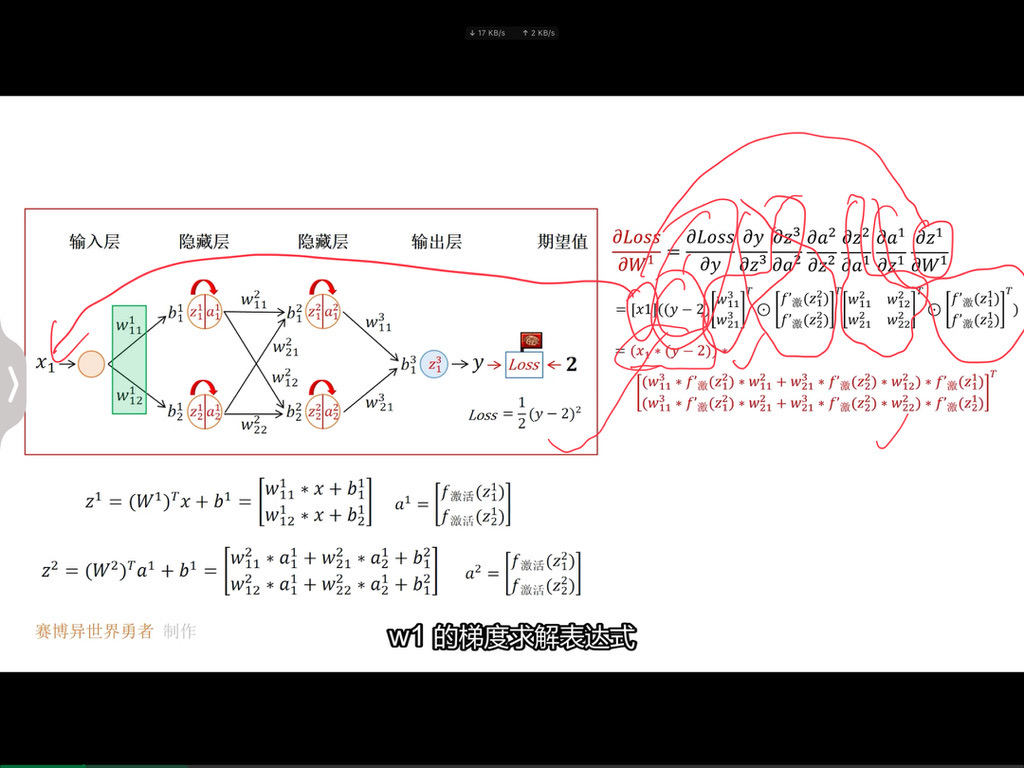
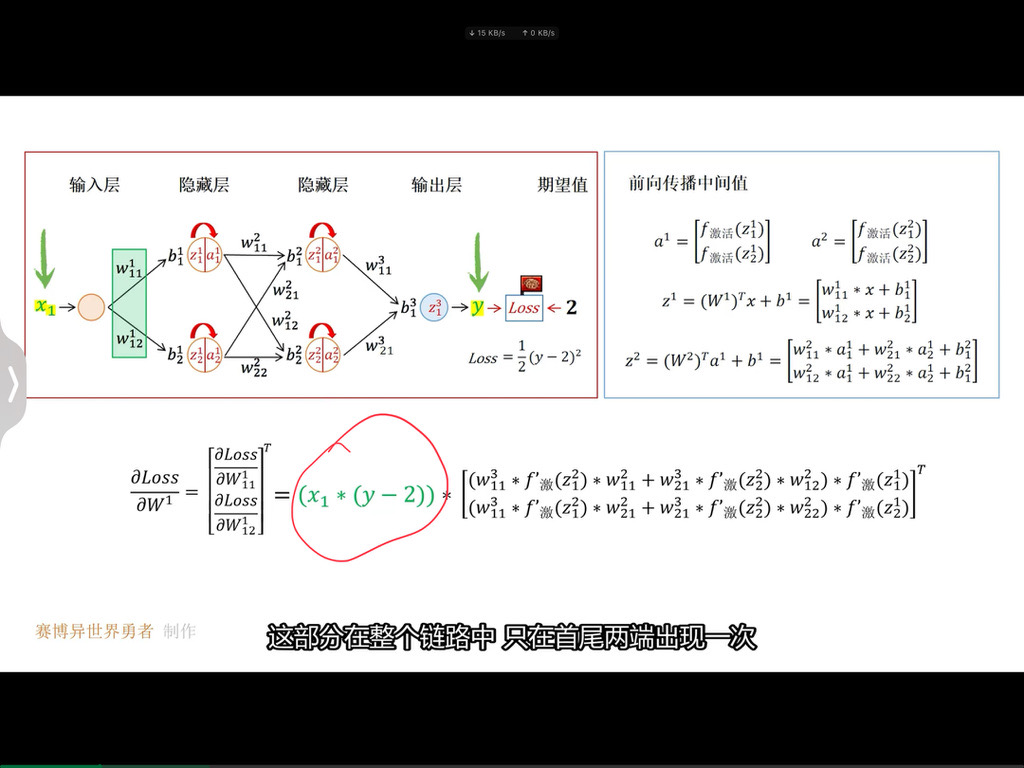
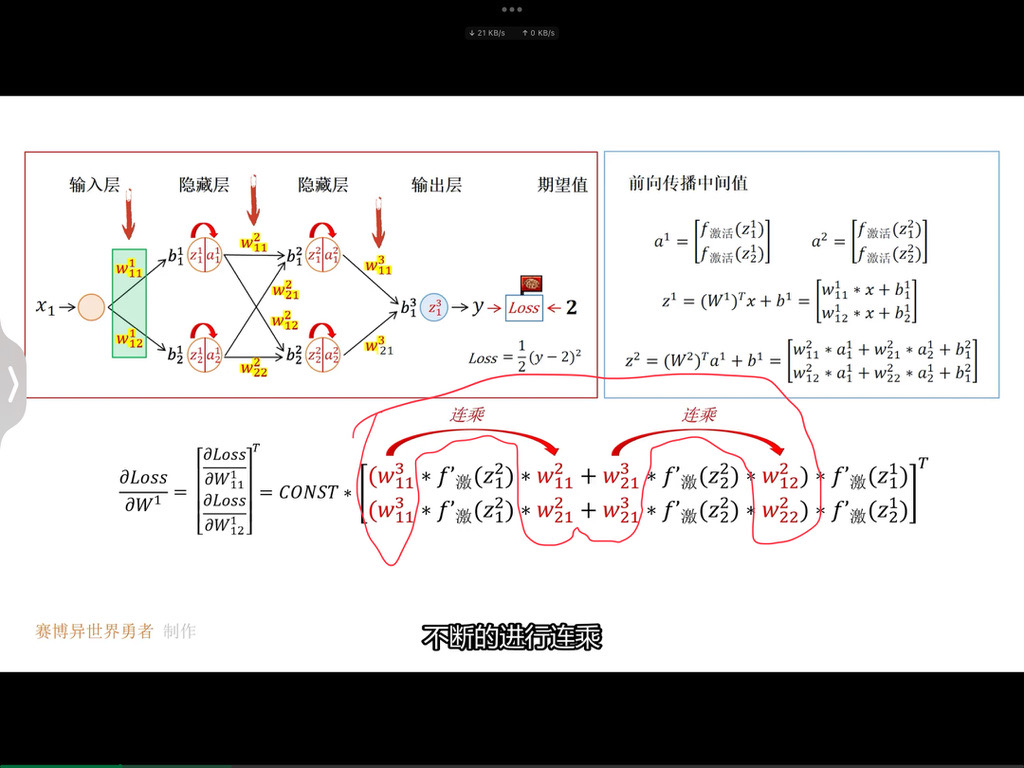
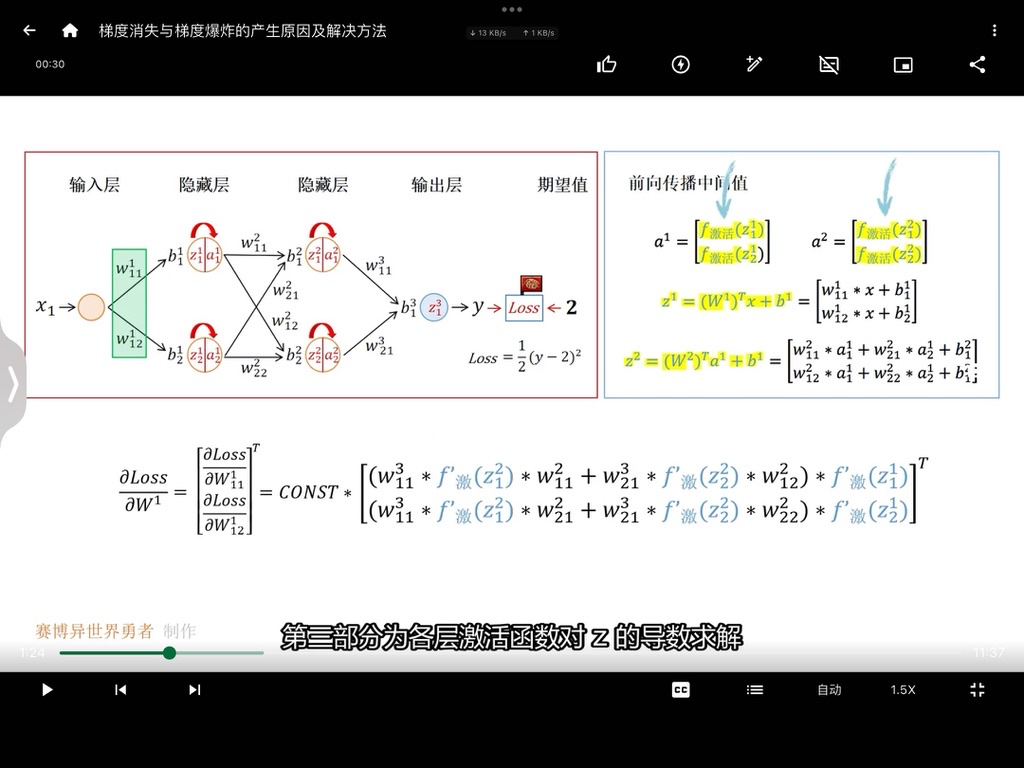
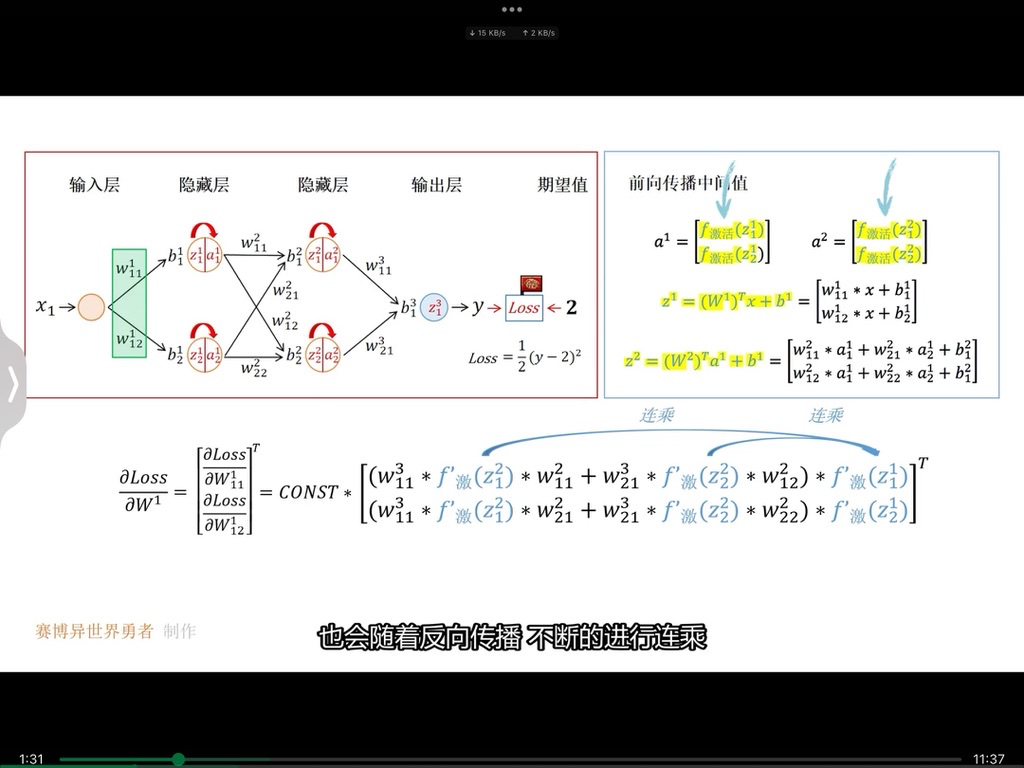
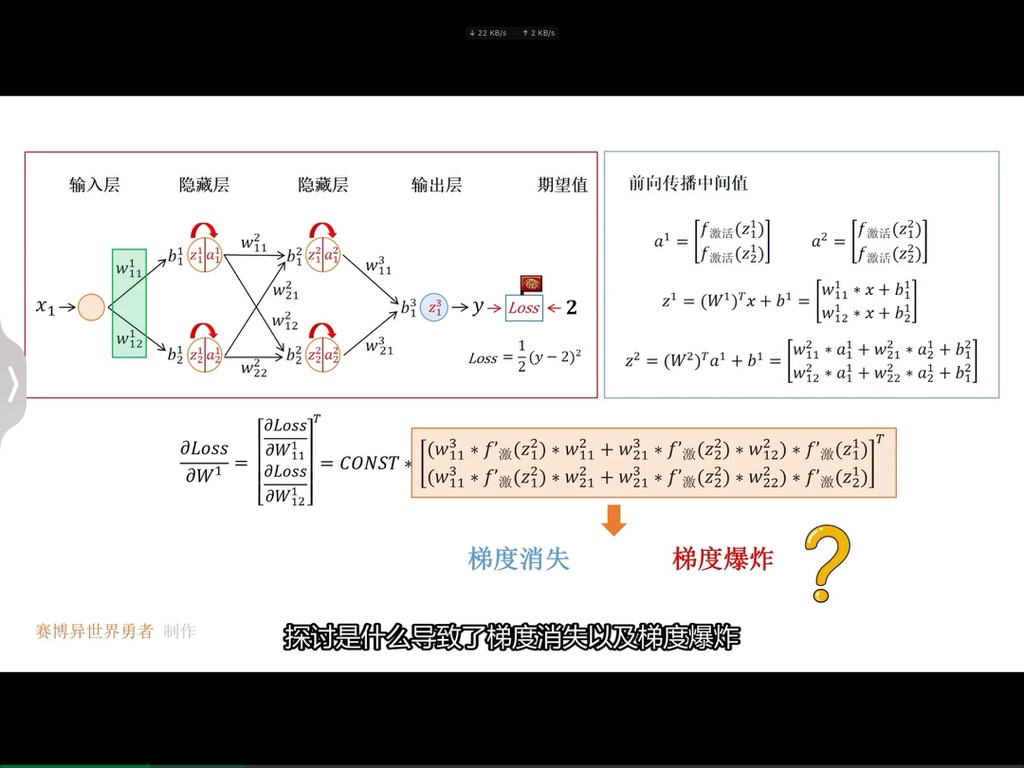
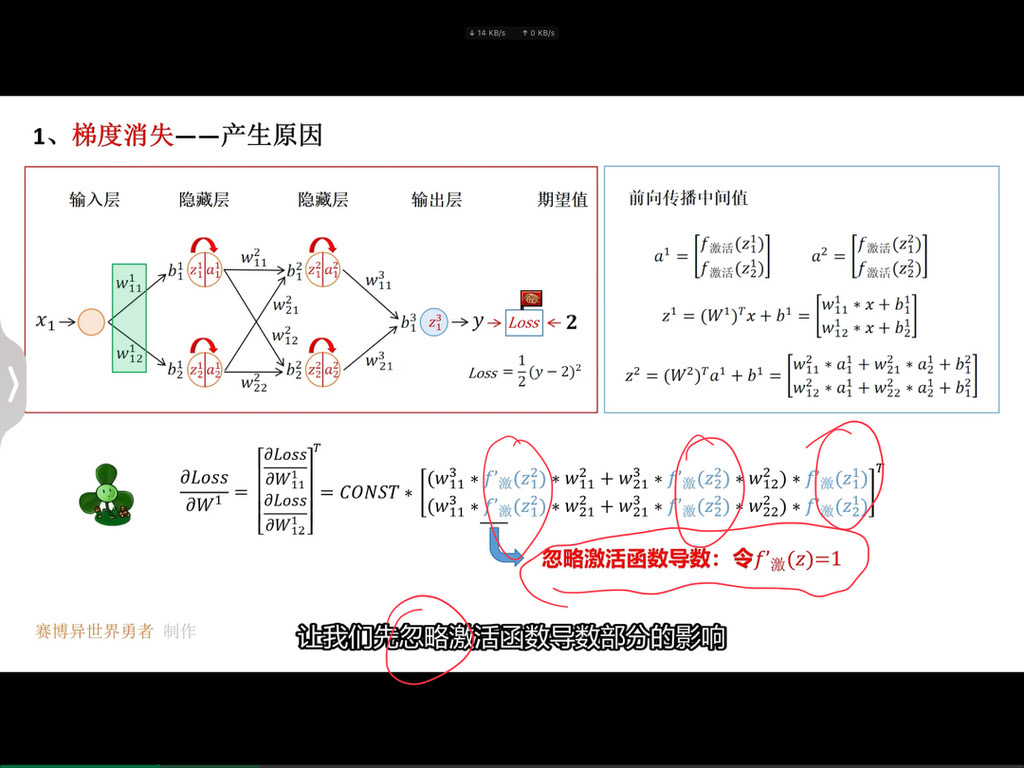
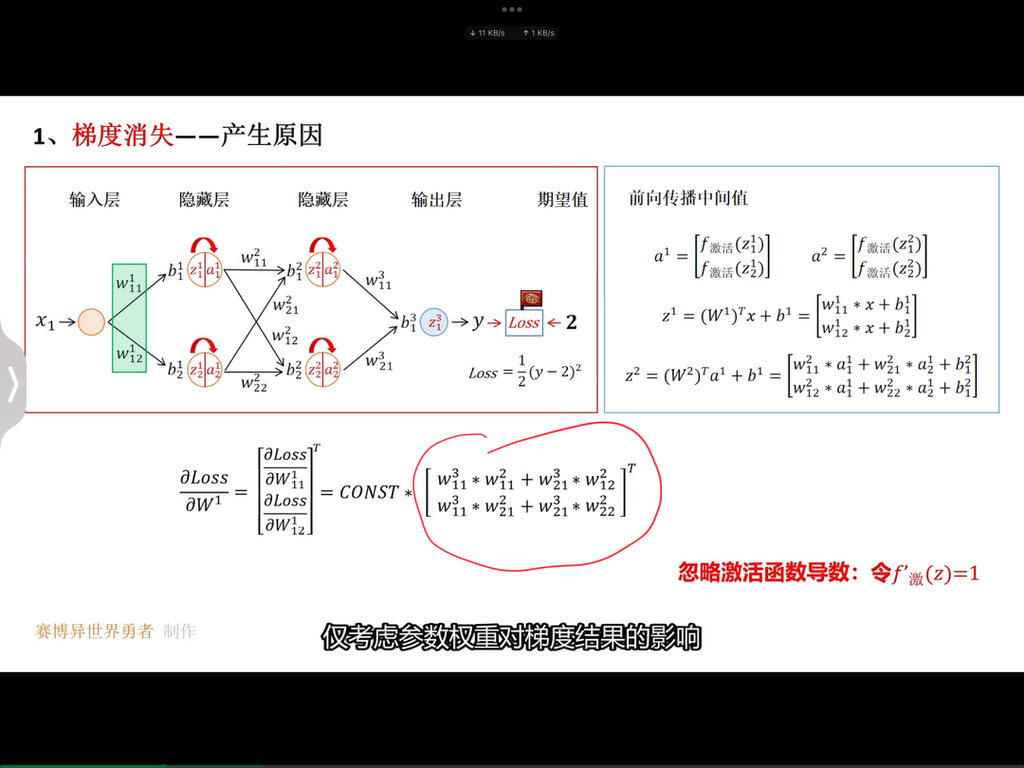
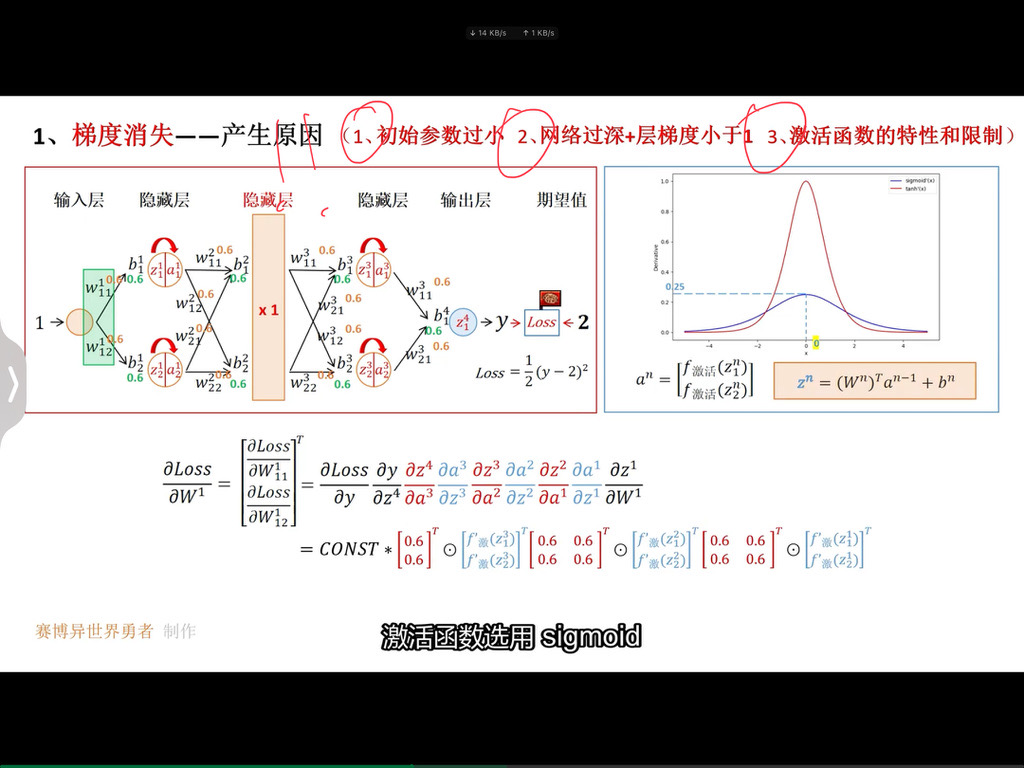
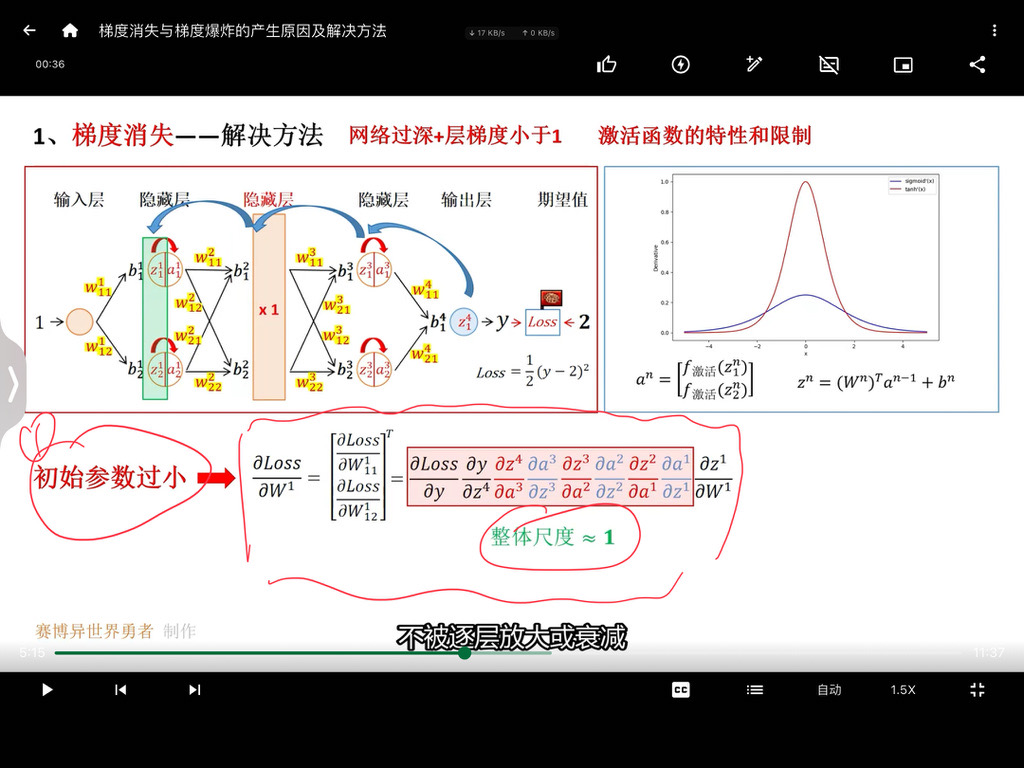
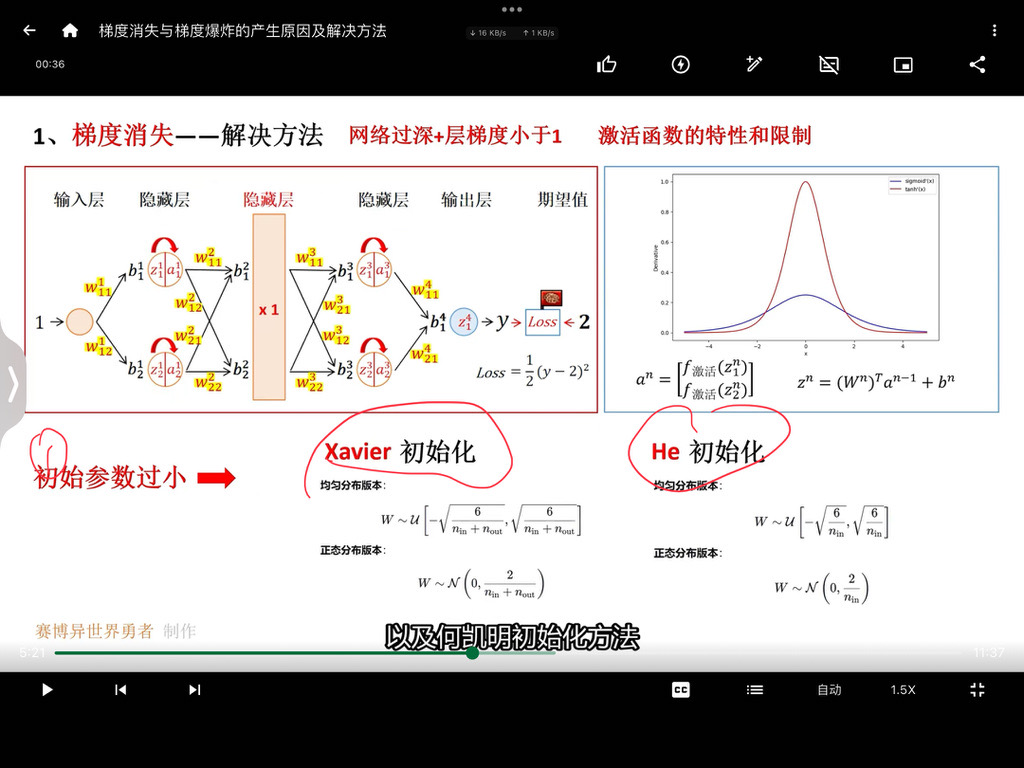
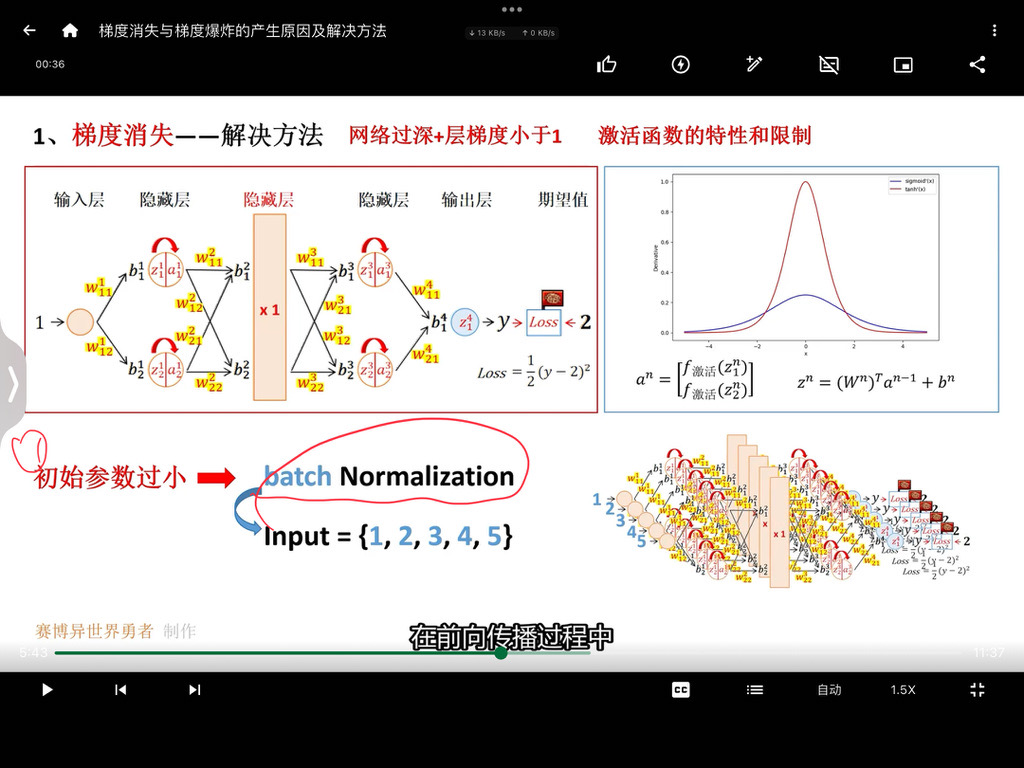
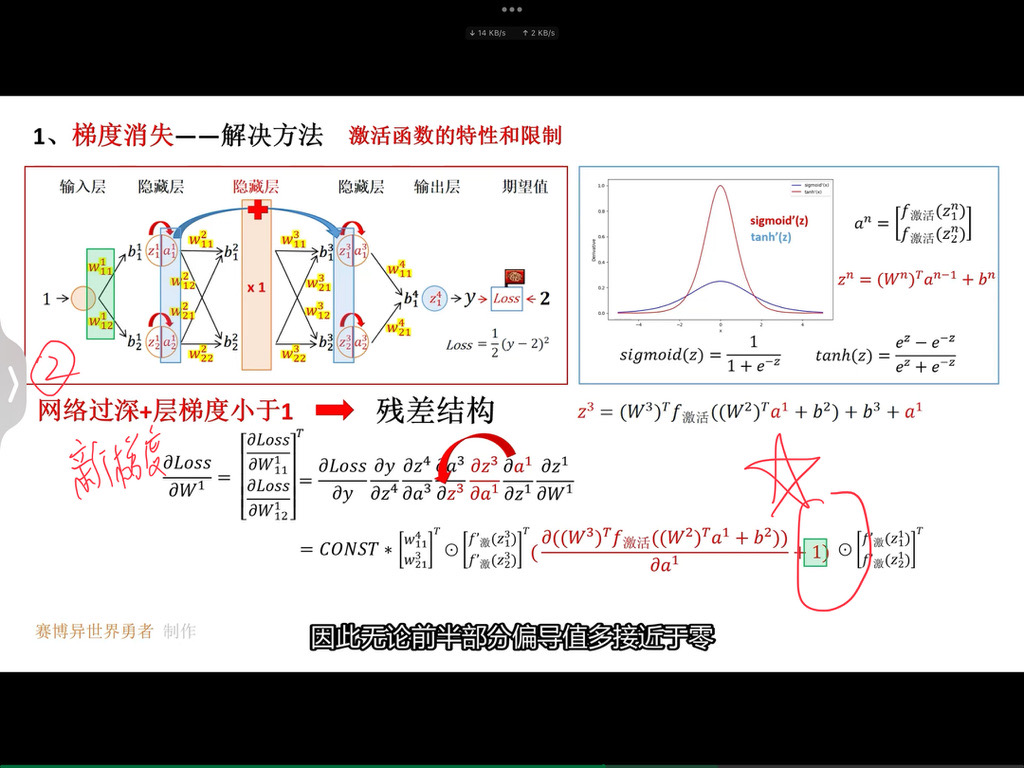
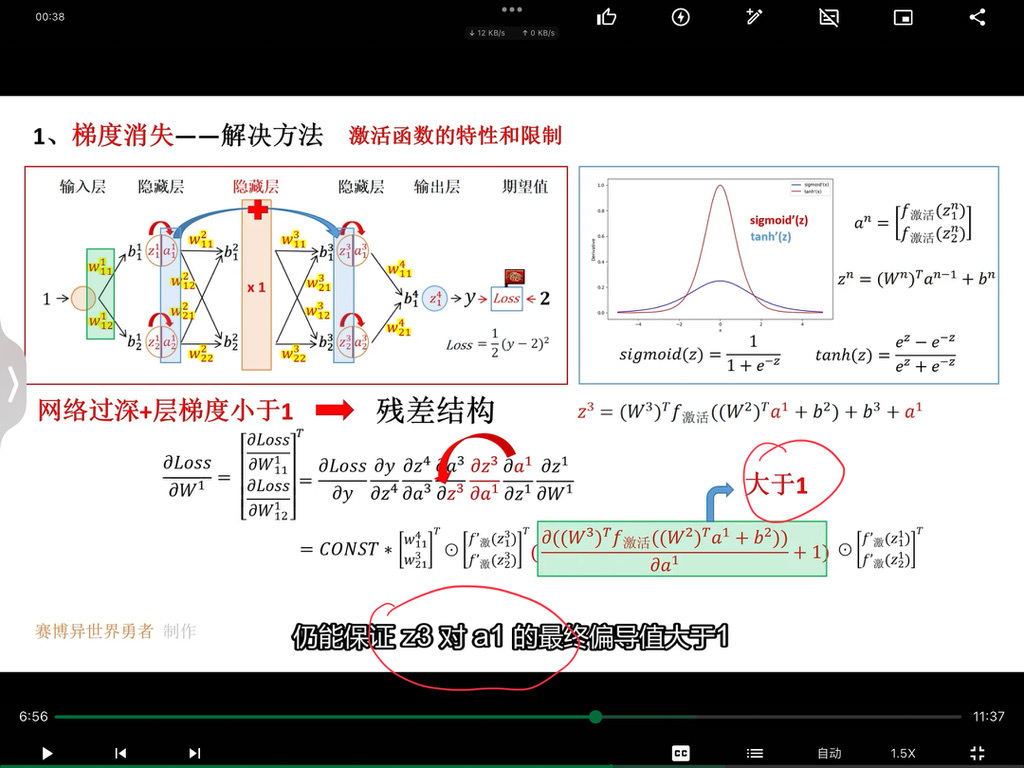
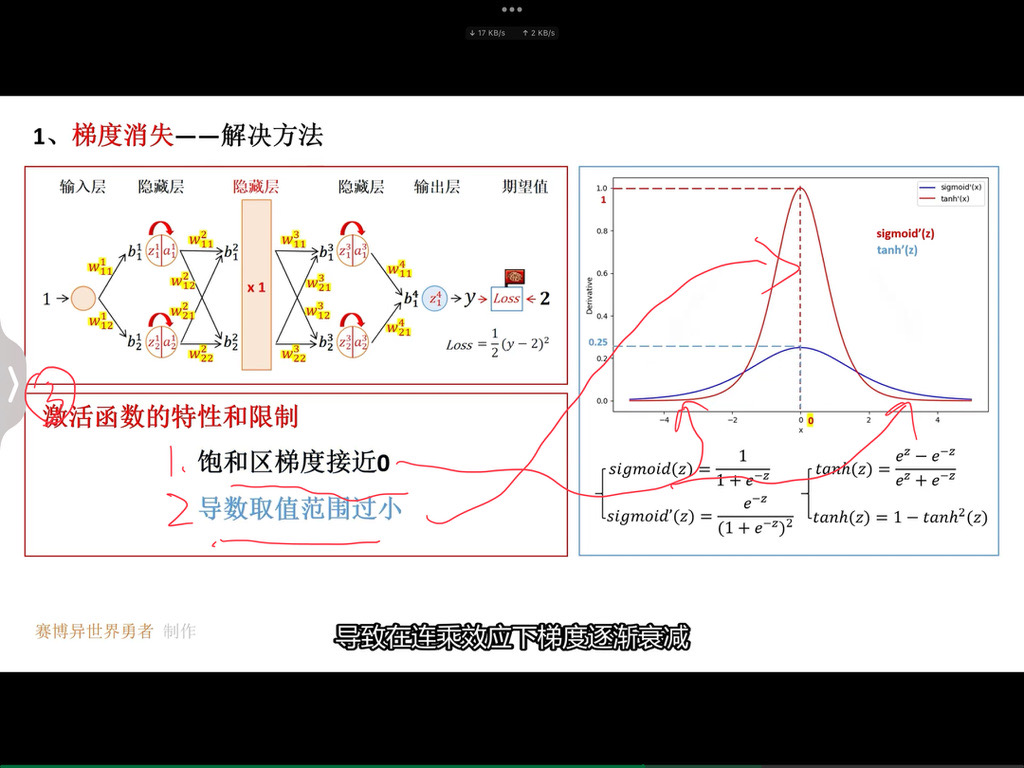
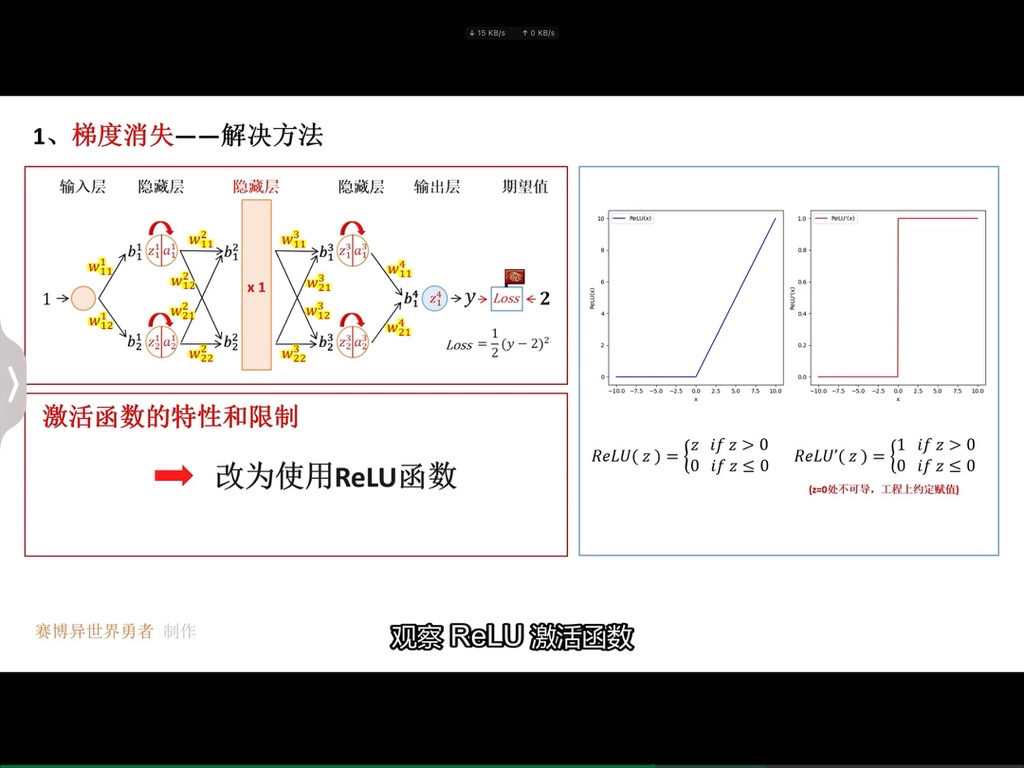
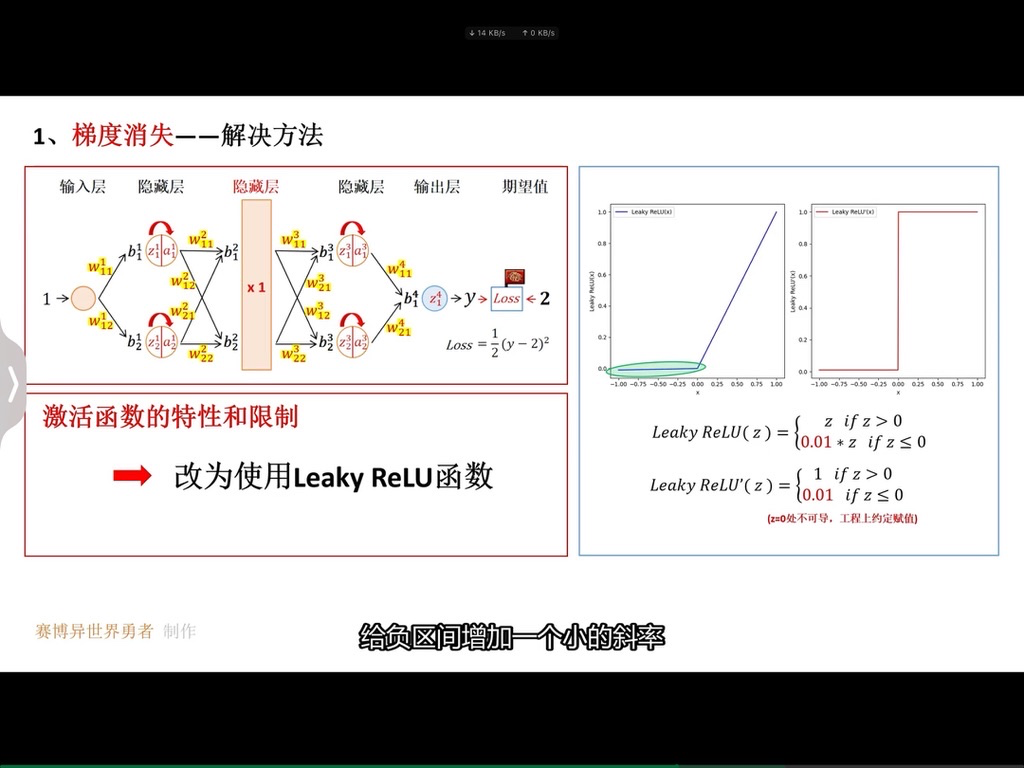
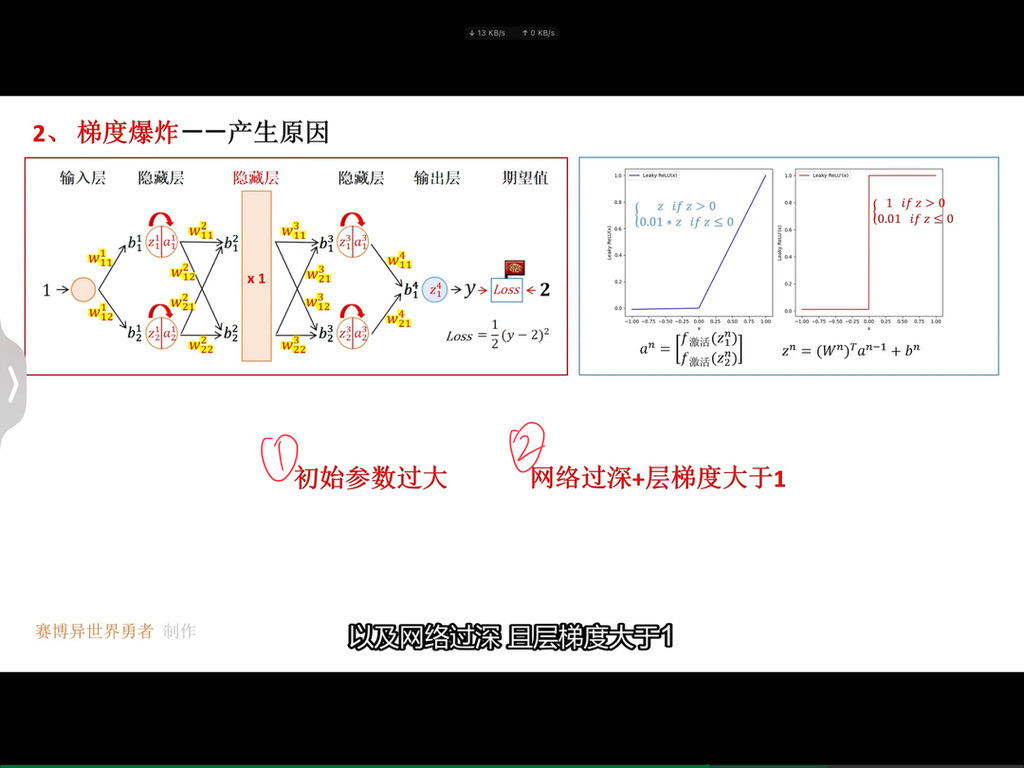
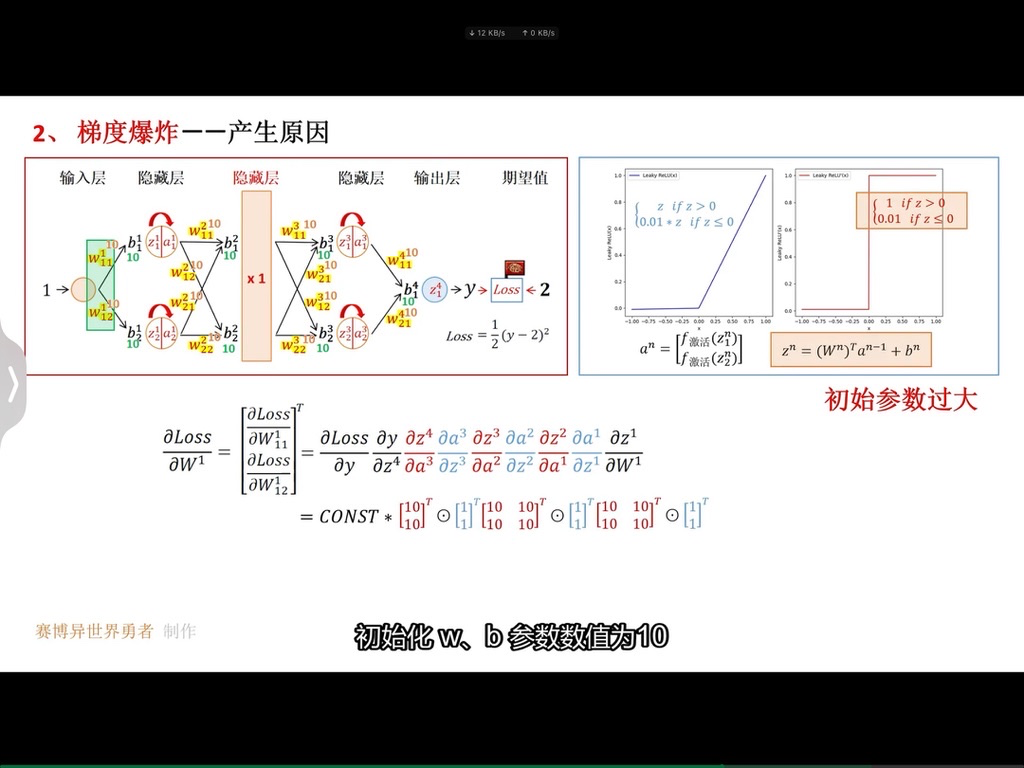
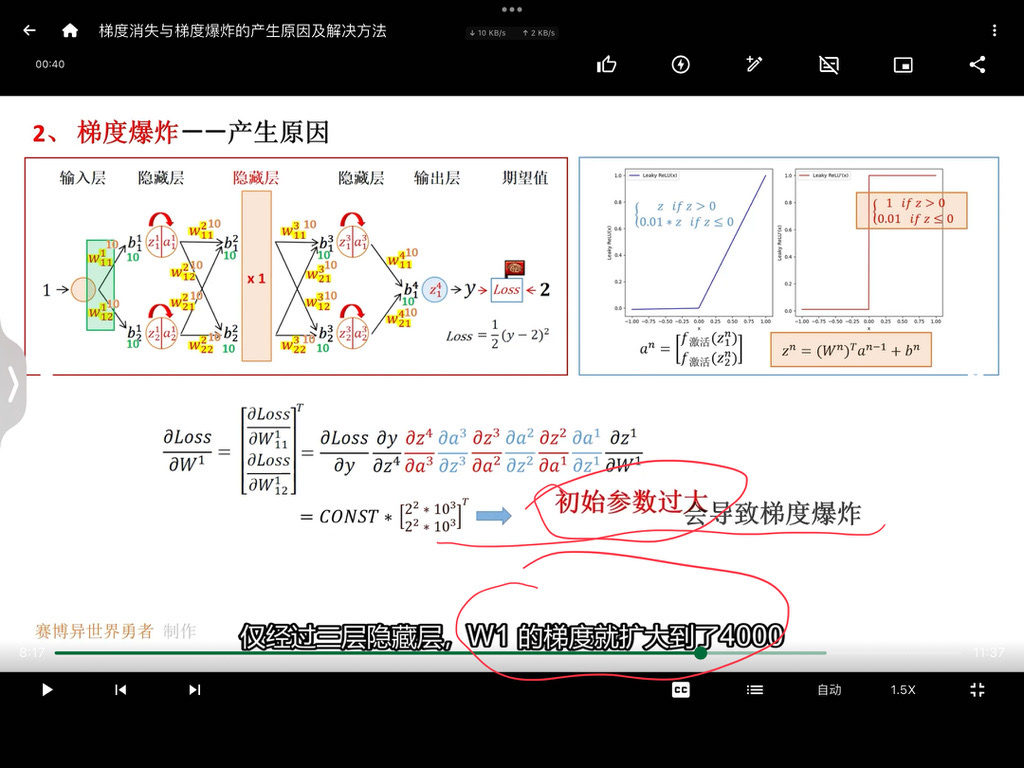
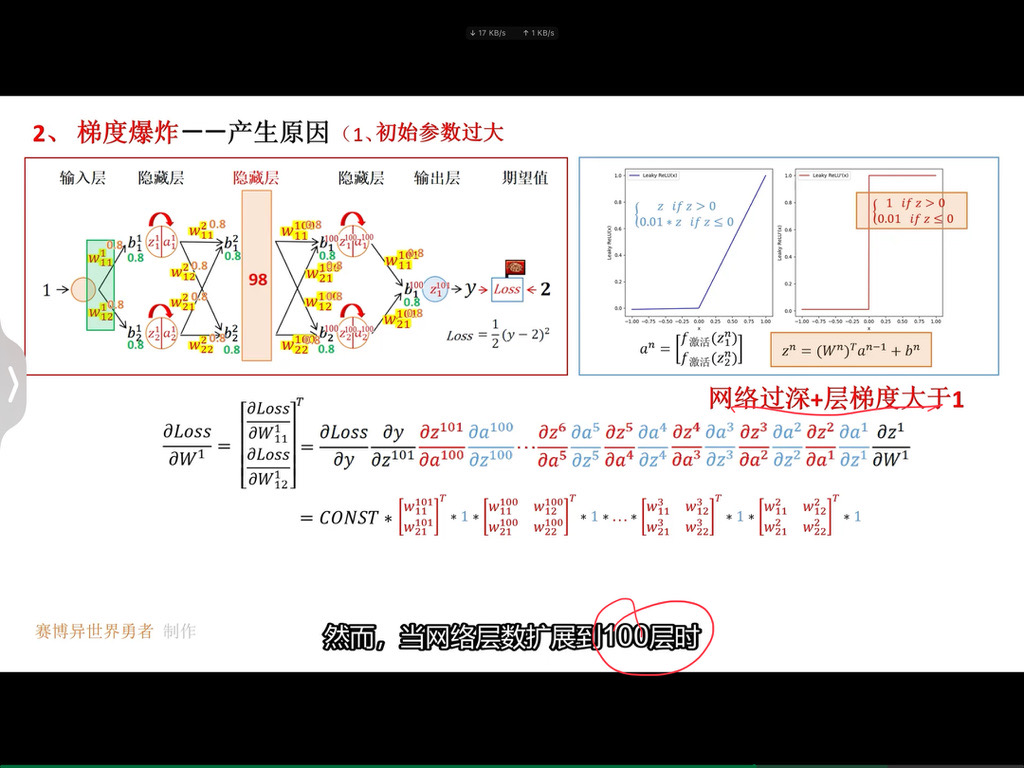
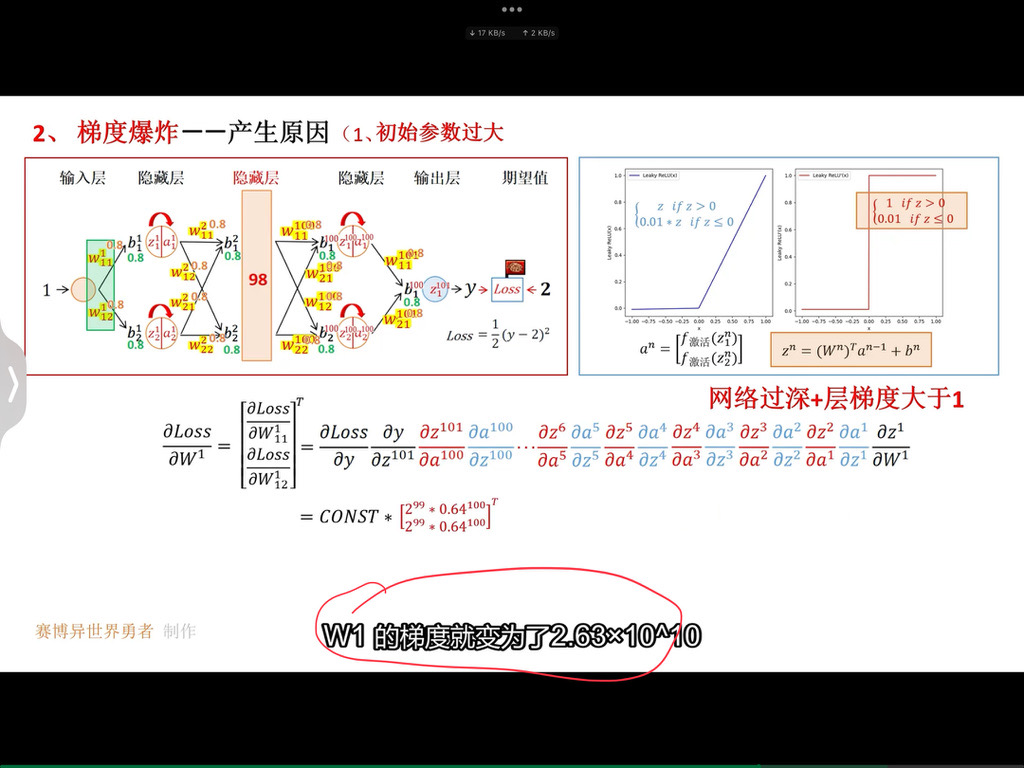
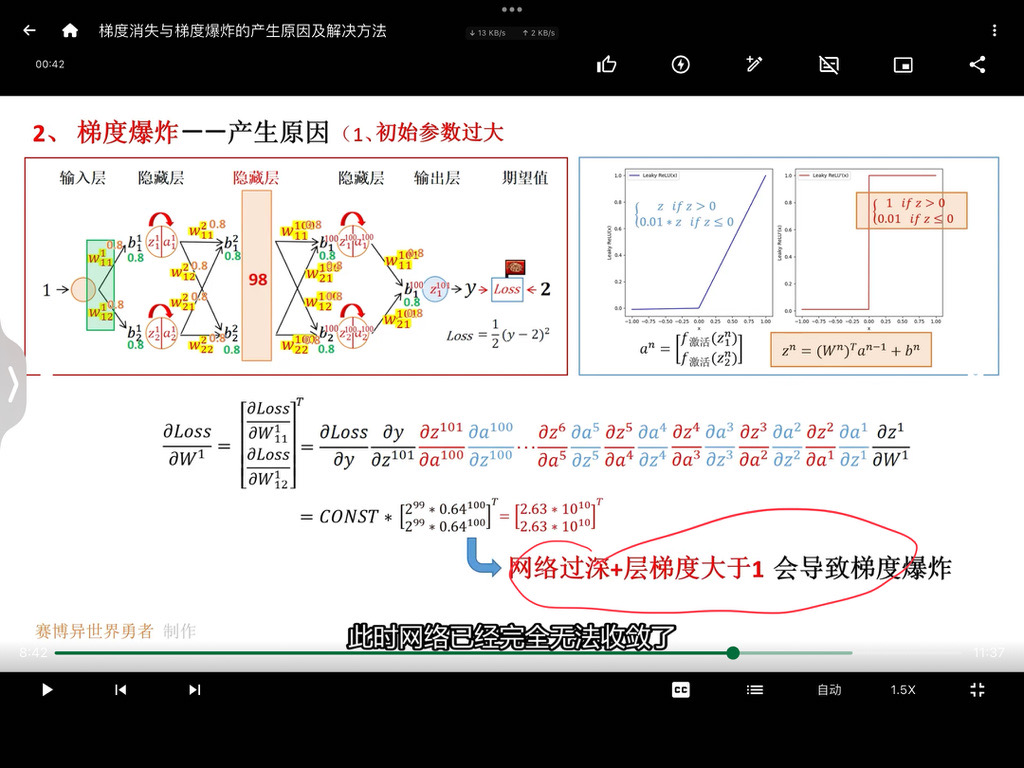
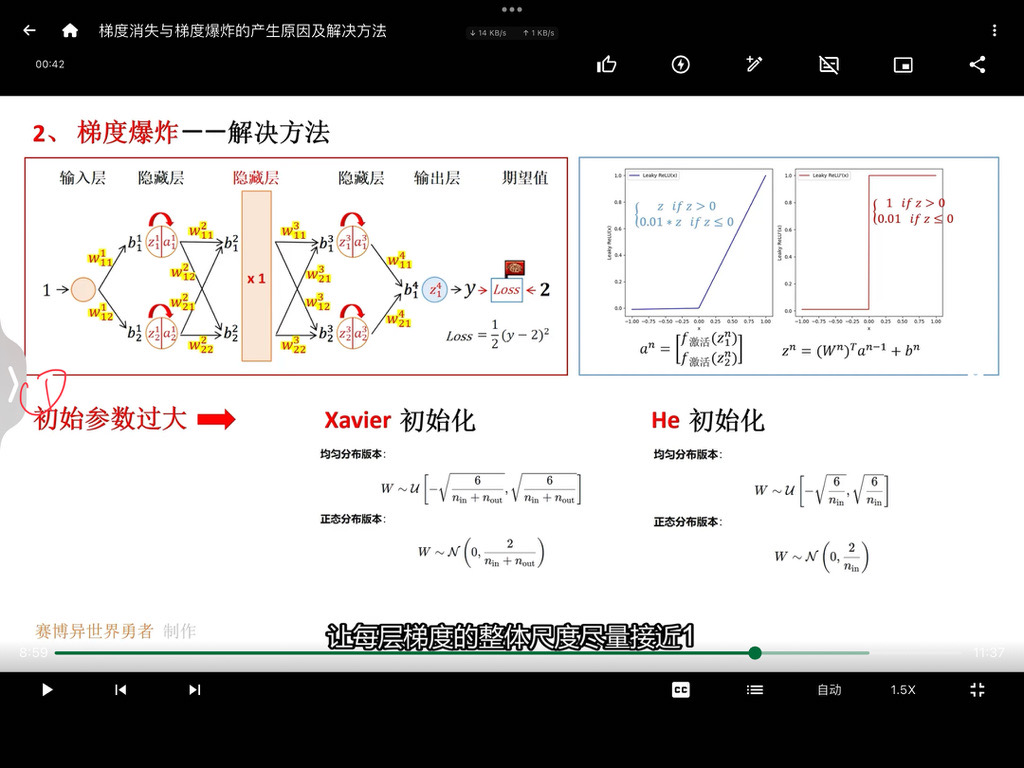
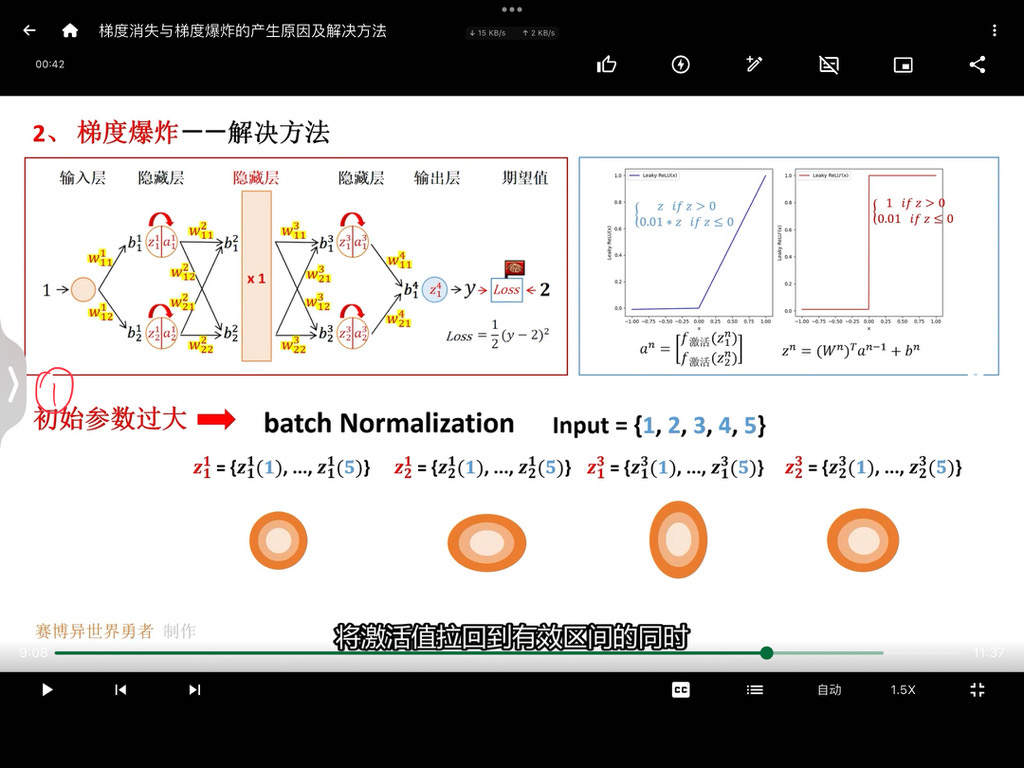

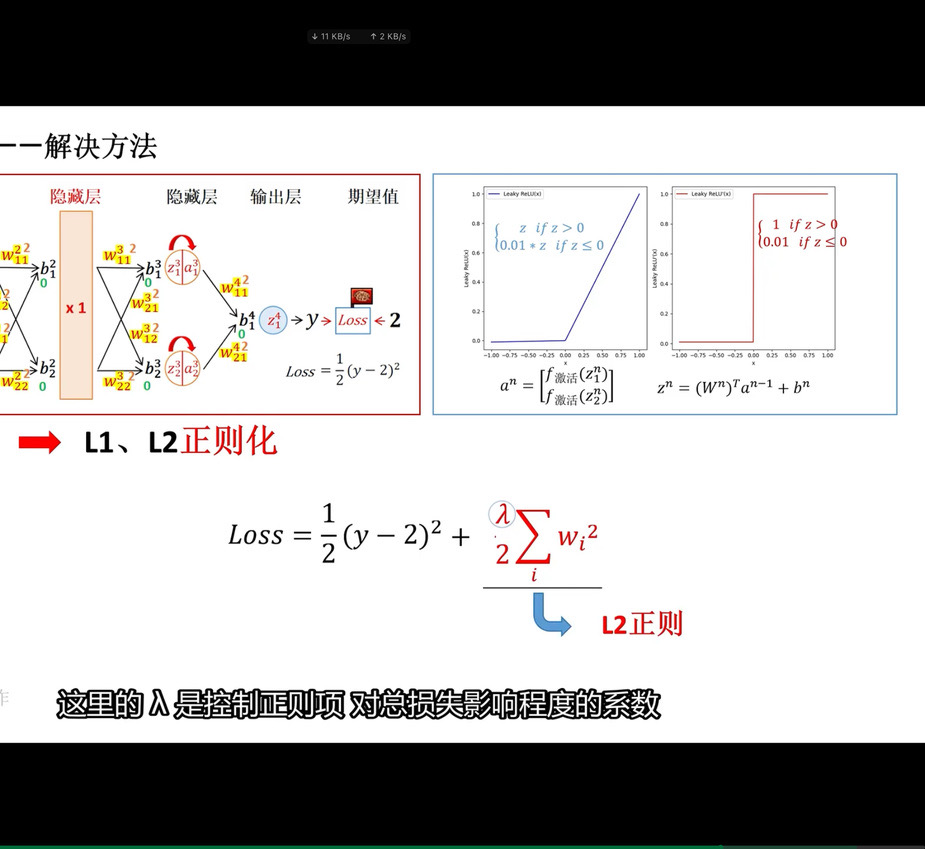
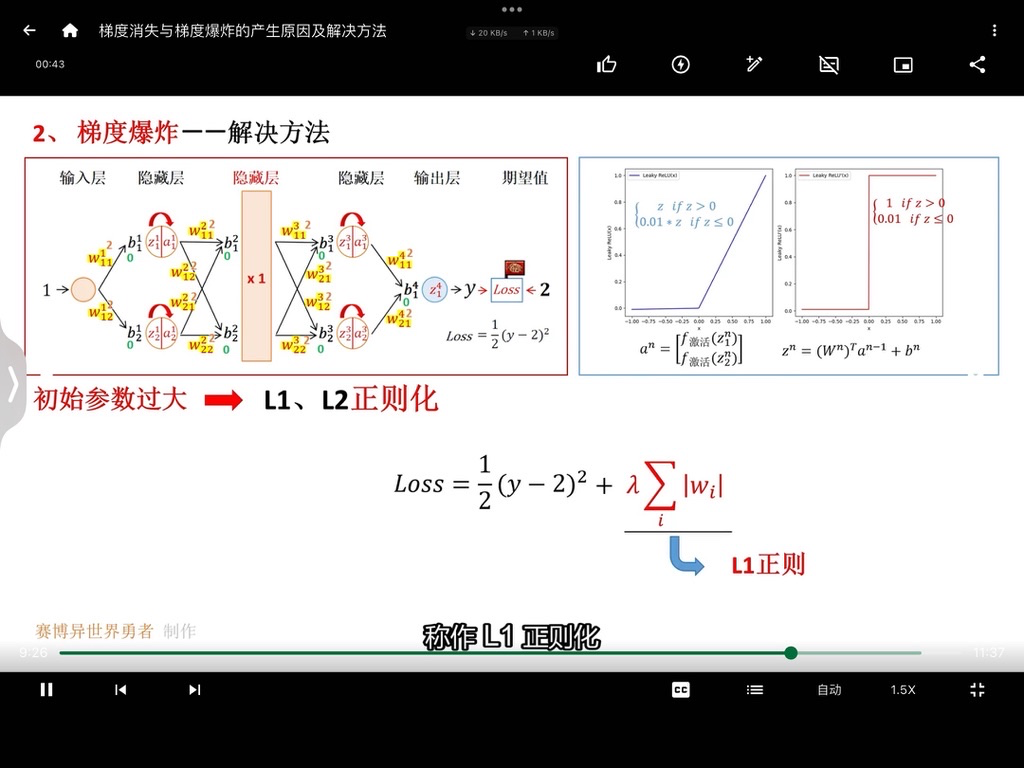
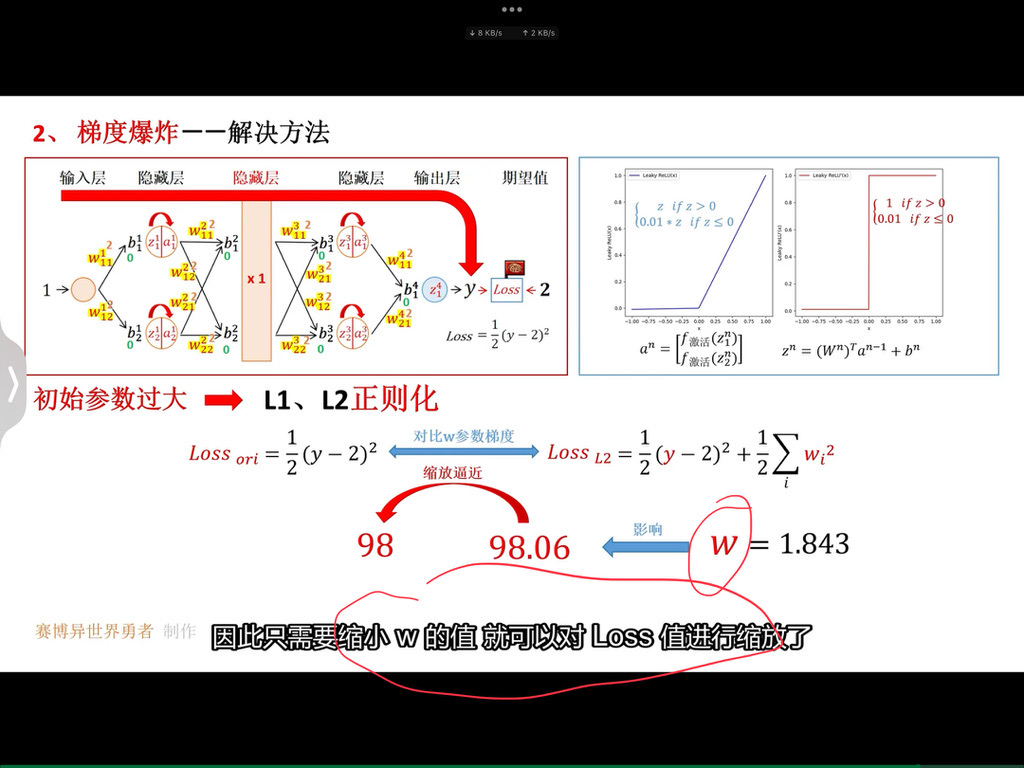
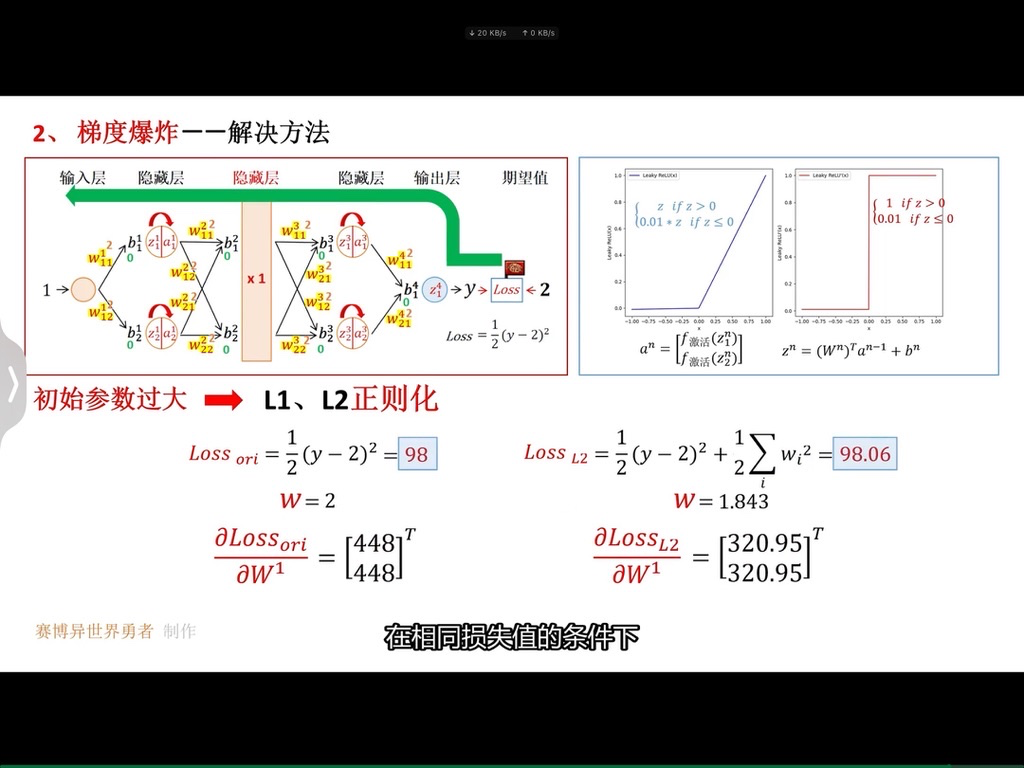
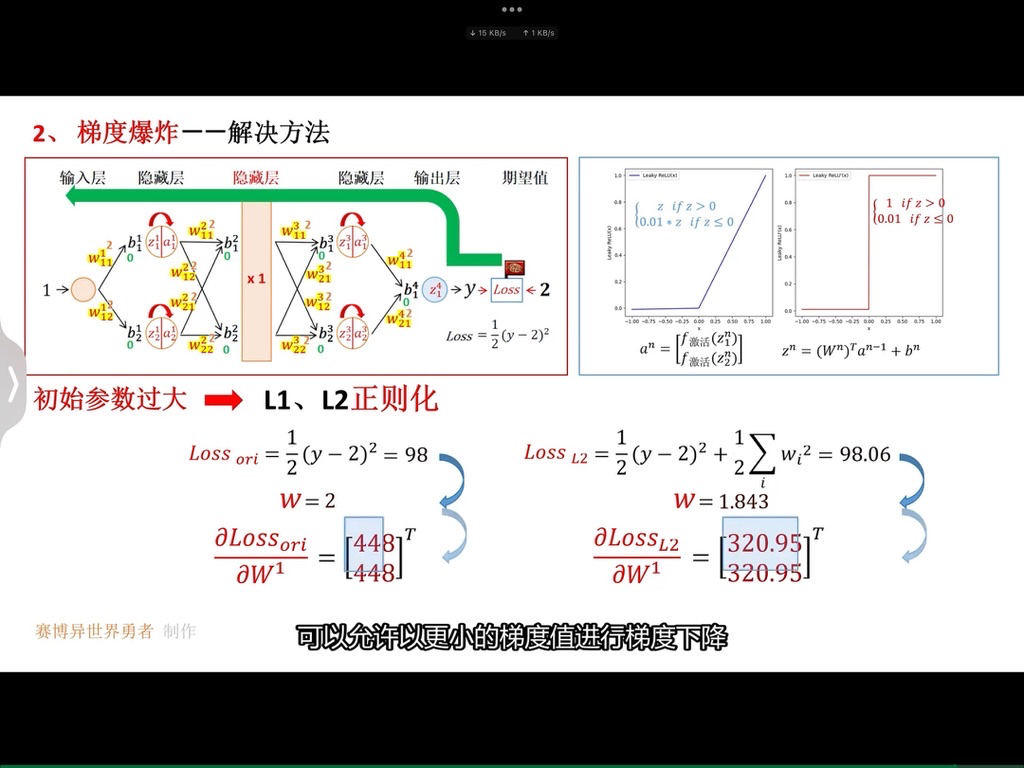
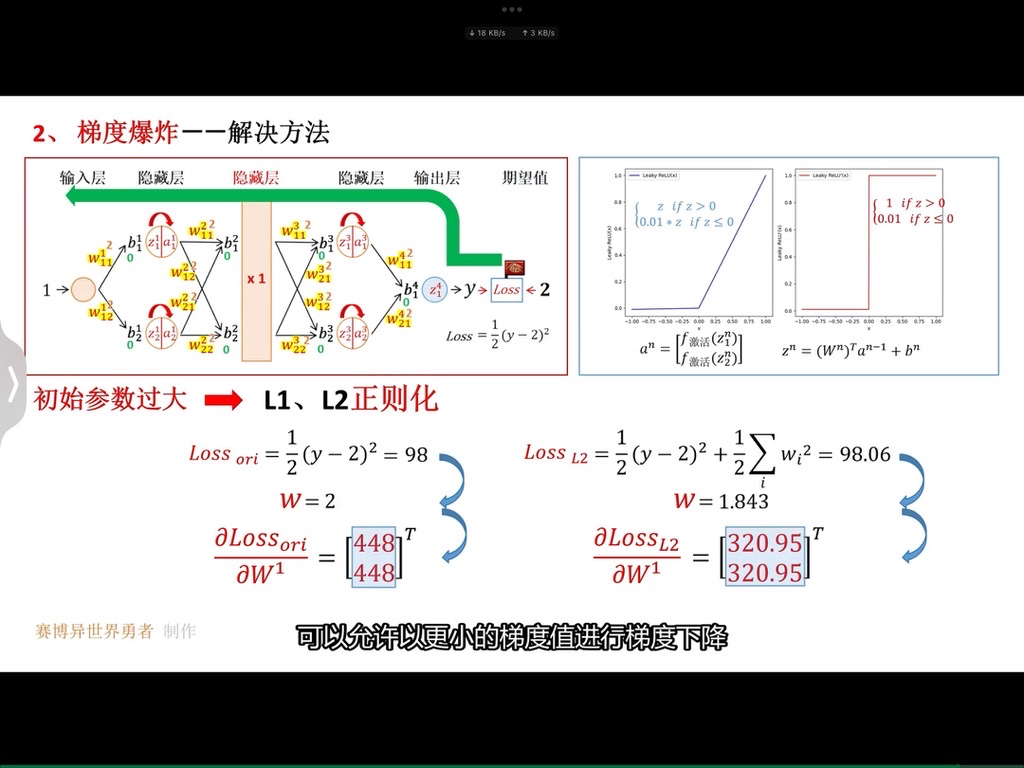
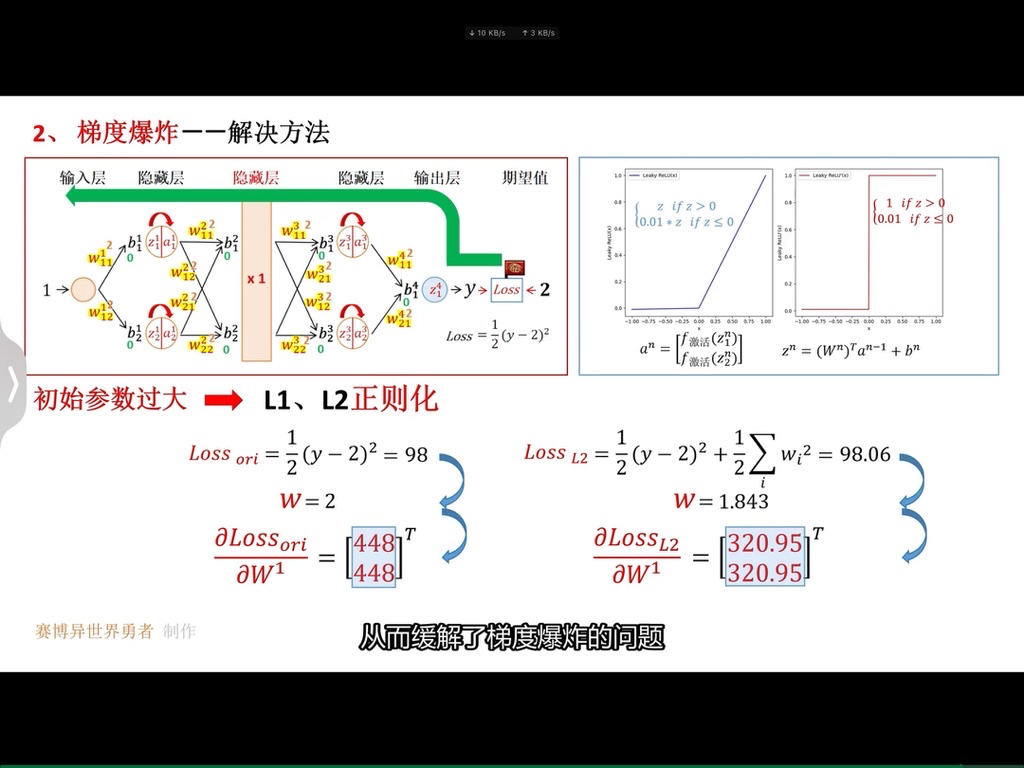
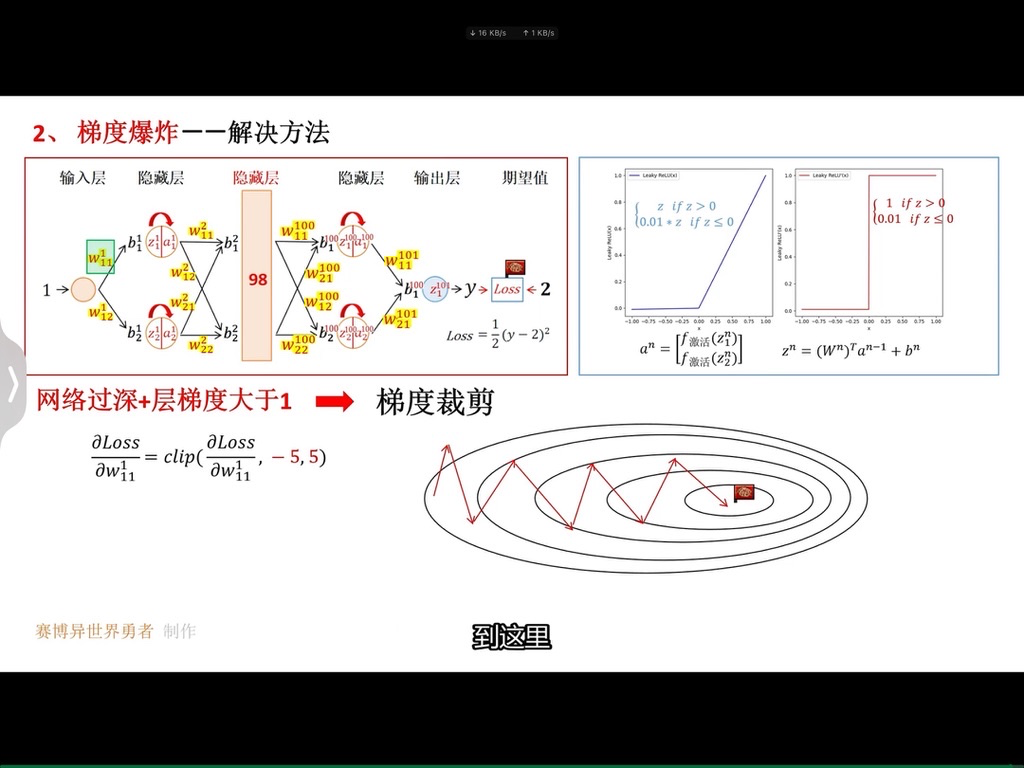
pytorch代码分析:
如何理解下面的代码:
1 | class Net(nn.Module): |
这段代码是一个简单的神经网络模型的定义,使用 PyTorch 框架来构建。让我解释一下这段代码的含义:
- class Net(nn.Module)::定义了一个名为 Net 的类,继承自 nn.Module 类,表示这个类是一个神经网络模型。
2. def init(self, n_feature, n_hidden, n_output)::定义了 Net** 类的构造函数 init,该函数接受三个参数 n_feature、n_hidden 和 n_output,分别表示输入特征的数量、隐藏层神经元的数量和输出的数量。**
3. super(Net, self).__init__():调用父类 nn.Module** 的构造函数,初始化神经网络模型。**
4. self.layer = nn.Linear(n_feature, n_hidden):定义了一个线性层 layer,输入特征数量为 n_feature,输出特征数量为 n_hidden。
5. self.all_act = nn.Linear(n_hidden, n_output):定义了另一个线性层 all_act,输入特征数量为 n_hidden,输出特征数量为 n_output。
- def forward(self, x)::定义了前向传播函数 forward,接受输入 x,表示对输入数据进行前向传播计算。
- x = self.layer(x):将输入 x 经过 layer 线性层的计算,得到隐藏层的输出。
- x = torch.tanh(x):对隐藏层的输出应用双曲正切函数(tanh)作为激活函数,增加模型的非线性能力。
- x = self.all_act(x):将经过激活函数后的隐藏层输出再经过 all_act 线性层的计算,得到最终的输出。
- return x:返回神经网络模型的输出。
这段代码定义了一个简单的神经网络模型,包括一个输入层到隐藏层的线性变换和隐藏层到输出层的线性变换,中间使用了双曲正切函数作为激活函数。在神经网络的训练过程中,可以通过调用 forward 函数来进行前向传播计算。
x.transpose(1, 2)
import torch
x = torch.randn(10, 3, 5) # 创建一个形状为(10, 3, 5)的张量 x_transposed = x.transpose(1, 2) # 将x的形状变为(10, 5, 3)
nn.Parameter
nn.Parameter是PyTorch中的一个类,用于将一个张量(Tensor)转换为模型参数。这样,在训练过程中,这个参数会被自动加入到模型的参数列表中,并参与梯度更新。
用途
- 可学习参数:
nn.Parameter的主要用途是将张量转换为可学习的参数。在训练过程中,这些参数会被优化器更新,以最小化损失函数。 - 模型参数管理:
nn.Parameter使得模型参数的管理更加方便。通过将张量转换为nn.Parameter,可以自动地将它们加入到模型的参数列表中,并可以在训练过程中进行优化。
示例
1 | import torch |
注意事项
- 自动注册:当将一个张量转换为
nn.Parameter时,它会自动注册到模型的参数列表中。这意味着在调用model.parameters()时,这个参数会被返回。 - 梯度计算:
nn.Parameter会自动参与梯度计算。在反向传播过程中,PyTorch会自动计算这个参数的梯度,并将其存储在grad属性中。 - 初始化:
nn.Parameter的初始化通常使用标准正态分布或均匀分布,但也可以根据具体任务和模型结构选择其他初始化方法。
通过使用
nn.Parameter,可以方便地管理模型的可学习参数,并使其在训练过程中参与优化。
1 | import torch |
transformer位置嵌入
在Transformer模型中,位置嵌入(Positional Embedding)的加入是为了解决序列数据中缺少位置信息的问题。Transformer模型的核心思想是自注意力(Self-Attention)机制,它能够捕捉序列中任意两个元素之间的依赖关系,但自注意力机制本身并不包含位置信息。因此,为了使模型能够理解序列中元素的顺序,需要通过位置嵌入来显式地引入位置信息。
位置嵌入的作用
- 保持序列顺序:在自然语言处理(NLP)任务中,单词的顺序对句子的含义至关重要。通过位置嵌入,模型可以知道每个单词在句子中的位置,从而保持原始序列的顺序。
- 捕捉相对位置:在计算机视觉(CV)任务中,图像中的像素位置对图像内容的理解也非常重要。通过位置嵌入,模型可以捕捉到像素之间的相对位置关系。
- 提高模型性能:引入位置嵌入后,模型能够更好地理解序列数据的顺序和结构,从而提高模型的性能。
位置嵌入的实现
在Transformer模型中,位置嵌入通常通过一个可学习的参数来实现。这个参数是一个张量,其形状为
(seq_len, d_model),其中
seq_len是序列长度,d_model是模型的隐藏层维度。在模型的前向传播过程中,位置嵌入会被添加到输入序列中,作为输入的一部分。
位置嵌入的初始化
位置嵌入的初始化通常使用正弦和余弦函数。对于位置 p和维度
2i,位置嵌入的值可以通过以下公式计算:
1 | PE_{(p, 2i)} = sin(p / 10000^(2i / d_model)) |
其中,p是位置索引,i是维度索引,d_model是模型的隐藏层维度。
通过这种方式,位置嵌入能够为模型提供丰富的位置信息,从而提高模型的性能。
1 | import torch |
nn.Dropout
nn.Dropout是PyTorch中的一个模块,用于在训练过程中对神经网络的输入或输出进行随机失活(dropout)。这种技术有助于防止过拟合,提高模型的泛化能力。
用途
- 防止过拟合:在训练过程中,
nn.Dropout会随机将一部分输入单元的输出设置为0,从而减少模型的复杂度,防止过拟合。 - 正则化:
nn.Dropout是一种正则化技术,通过在训练过程中随机失活一部分输入单元,可以减少模型的方差,从而提高模型的泛化能力。
示例
1 | import torch |
在这个示例中,我们创建了一个
nn.Dropout层,并使用它对输入张量进行前向传播。p参数表示失活概率,即每个输入单元被设置为0的概率。在这个示例中,p被设置为0.5,表示每个输入单元有50%的概率被设置为0。
注意事项
- 训练和评估:在训练过程中,
nn.Dropout会随机失活一部分输入单元。在评估过程中,nn.Dropout不会进行随机失活,而是直接输出输入单元的输出。 - 可学习性:
nn.Dropout不是一个可学习的参数,它不会在训练过程中更新。然而,它的失活概率p可以是一个可学习的参数,可以通过优化器进行更新。
通过使用
nn.Dropout,可以有效地防止过拟合,提高模型的泛化能力。
nn.BatchNorm1d
1. 定义与作用
- 功能:对每个特征通道(feature
channel)进行归一化,使输出的均值为0、方差为1,并通过可学习的参数(缩放因子
gamma和平移因子beta)恢复数据的表达能力。 - 适用场景:主要用于全连接层(如输入形状为
(batch_size, num_features))或时间序列(如输入形状为(batch_size, num_features, sequence_length))。
2. 数学原理
归一化公式: 对输入数据
x,计算当前批次的均值μ和方差σ²,然后进行标准化:\[ \hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \]
最终输出为:
\[ y = \gamma \cdot \hat{x} + \beta \]
其中
ϵ是为数值稳定性添加的小常数。
3. 关键参数与配置****
num_features:输入数据的特征维度(必须与输入的第二维一致)。eps(默认1e-5):防止除以零的修正项。momentum(默认0.1):用于更新全局均值/方差的动量参数,控制历史统计量的衰减速度。affine(默认True):是否启用可学习的gamma和beta参数。
4. 训练与推理模式的行为差异****
- 训练阶段:基于当前批次计算均值和方差,并更新全局移动平均统计量。
- 推理阶段:使用训练时累积的全局均值和方差进行归一化,而非当前批次数据。
5. 应用场景与示例****
- 全连接层后:常用于全连接层与激活函数之间,加速收敛。
1
2
3
4
5
6import torch.nn as nn
model = nn.Sequential(
nn.Linear(128, 64),
nn.BatchNorm1d(64), # 输入特征数为64
nn.ReLU()
) - 时间序列处理:在RNN中,可对每个时间步的特征进行归一化(需调整输入形状)。
6. 与其他归一化层的对比****
- 与
LayerNorm的区别:BatchNorm1d在特征维度归一化,依赖批次数据;LayerNorm则在样本维度归一化,适用于动态网络(如Transformer)。 - 与
InstanceNorm1d的区别:后者对每个样本的每个通道单独归一化,常用于生成任务。
注意事项
- 小批量问题:当
batch_size过小时,统计量估计不准确,可能影响性能。 - 模式切换:训练时需调用
model.train(),推理时调用model.eval()以固定统计量。
通过合理使用
nn.BatchNorm1d,可以显著提升模型训练的稳定性和收敛速度,尤其在深层网络中效果更为明显。
何时应避免使用?
- 数据分布极度不平衡或特征间强相关时,批归一化可能削弱模型表达能力;(特征间强相关指的是数据集中不同特征之间存在高度线性或非线性关系,比如一个特征可以部分或完全由另一个特征推导出来,比如遥感曲线就不适合使用)
- 生成对抗网络(GAN)中,部分研究表明批归一化可能导致模式崩溃,需谨慎使用。
nn.BatchNorm1d 和
nn.LayerNorm的差异
nn.BatchNorm1d 和 nn.LayerNorm
是深度学习中两种常用的归一化方法,尽管目标相似(加速训练、稳定梯度),但它们在实现逻辑、适用场景和数学原理上存在显著差异。以下从多个维度对比两者的区别:
1. 归一化维度的差异
nn.BatchNorm1d:在特征维度(feature dimension)上对每个通道独立归一化。- 输入形状为
(batch_size, num_features)时,计算每个特征通道的均值和方差(跨批次样本)。 - 例如,输入为
(32, 64)(32个样本,64个特征),会对64个特征分别计算32个样本的均值和方差。
- 输入形状为
nn.LayerNorm:在样本维度(sample dimension)上对每个样本的所有特征归一化。- 输入形状为
(batch_size, num_features)时,计算每个样本的均值和方差(跨该样本的所有特征)。 - 例如,输入为
(32, 64),会对每个样本的64个特征单独计算均值和方差,生成32个归一化结果。
- 输入形状为
2. 统计量的计算方式
BatchNorm1d:- 依赖当前批次的数据计算均值和方差,训练时通过移动平均累积全局统计量,推理时使用固定值。
- 对批次大小敏感,小批量可能导致统计量估计不准确。
LayerNorm:- 仅依赖单个样本的数据计算均值和方差,训练和推理时的行为一致,无需存储全局统计量。
- 对批次大小不敏感,适合动态网络(如变长序列或小批量场景)。
3. 应用场景的对比
BatchNorm1d的典型场景:- 全连接层或卷积层后,用于图像分类、时间序列预测等任务。
- 要求批次数据分布稳定,且批量较大(如ResNet、DenseNet)。
LayerNorm的典型场景:- 自然语言处理(NLP)中的Transformer、RNN等模型,处理变长序列或动态结构。
- 小批量训练(如BERT、GPT)或需要样本独立归一化的场景(如生成对抗网络)。
4. 参数设置与输入形状** **
BatchNorm1d:- 参数
num_features必须与输入的第二维(特征数)一致。 - 支持一维(全连接)、二维(时间序列)输入,如
(batch, features)或(batch, features, seq_len)。
- 参数
LayerNorm:- 参数
normalized_shape指定需归一化的维度(如特征维度或序列维度)。 - 支持任意形状输入,需显式指定归一化范围(如对
(batch, seq_len, features)输入,可设置normalized_shape=[seq_len, features])。
- 参数
5. 训练与推理的行为差异** **
BatchNorm1d:- 训练时:动态更新全局均值和方差的移动平均。
- 推理时:固定使用训练阶段累积的全局统计量。
LayerNorm:- 训练和推理时均基于当前输入样本计算统计量,无状态依赖,行为一致。
6. 优缺点对比** **
| 方法 | 优点 | 缺点 |
|---|---|---|
BatchNorm1d |
加速深层网络训练,缓解梯度问题 | 依赖大批量,对动态结构支持差 |
LayerNorm |
适应变长输入,适合小批量/动态网络 | 对特征间相关性敏感,可能损失信息 |
总结
- 选择依据:
- 若数据批次稳定且批量较大(如图像分类),优先使用
BatchNorm1d; - 若输入长度可变或需要样本独立处理(如NLP、生成模型),则选择
LayerNorm。
- 若数据批次稳定且批量较大(如图像分类),优先使用
- 核心区别:
BatchNorm1d归一化特征通道,依赖批次统计;LayerNorm归一化样本,依赖自身统计。
由小艺AI生成<xiaoyi.huawei.com>
1 |
|
1. BatchNorm1d 的计算过程
BatchNorm1d
对每个特征通道(列)独立计算均值和方差,跨批次样本归一化。
- 参数设置:假设
affine=False(即不学习缩放参数γ和偏移参数β),eps=0(简化计算)。 - 计算步骤:
- 特征通道1:样本1的值1,样本2的值4 → 均值 μ=(1+4)/2=2.5,方差 σ²=((1-2.5)²+(4-2.5)²)/2=2.25归一化结果:(1-2.5)/√2.25 = -1.5/1.5 = -1.0; (4-2.5)/1.5 = 1.0
- 特征通道2:值2和5 → μ=3.5,σ²=2.25 → 归一化结果:-1.0 和 1.0
- 特征通道3:值3和6 → μ=4.5,σ²=2.25 → 归一化结果:-1.0 和 1.0
- 输出结果:
1
2[[-1.0, -1.0, -1.0],
[ 1.0, 1.0, 1.0]] - 关键特点:每个特征通道的均值和方差来自不同样本的同一位置,输出后同一特征通道的分布均值为0、方差为1。
2. LayerNorm 的计算过程
LayerNorm
对每个样本(行)的所有特征独立计算均值和方差,归一化在样本内部进行。
- 参数设置:
normalized_shape=3(特征维度),elementwise_affine=False。 - 计算步骤:
- 样本1:特征值 [1,2,3] → μ=(1+2+3)/3=2.0,σ²=((1-2)²+(2-2)²+(3-2)²)/3=0.666归一化结果:(1-2)/√0.666≈-1.2247;(2-2)/√0.666=0;(3-2)/√0.666≈1.2247
- 样本2:特征值 [4,5,6] → μ=5.0,σ²=0.666 归一化结果:(4-5)/√0.666≈-1.2247;(5-5)/√0.666=0;(6-5)/√0.666≈1.2247
- 输出结果:
1
2[[-1.2247, 0.0, 1.2247],
[-1.2247, 0.0, 1.2247]] - 关键特点:每个样本的归一化独立进行,输出后每个样本的分布均值为0、方差为1。
对比总结
| 维度 | BatchNorm1d | LayerNorm |
|---|---|---|
| 归一化方向 | 跨样本,按特征通道归一化 | 跨特征,按样本内部归一化 |
| 统计量来源 | 依赖当前批次数据 | 仅依赖单个样本数据 |
| 适用场景 | 固定长度的全连接/卷积层(如图像分类) | 变长序列或动态结构(如NLP、Transformer) |
| 对批次的依赖 | 需要较大的批次稳定统计量 | 对批次大小不敏感 |
****直观理解****
- BatchNorm1d:假设输入是不同人的身高、体重、年龄数据,BatchNorm会分别对“身高”“体重”“年龄”这三个特征进行归一化,使得每个特征的分布标准化。
- LayerNorm:假设输入是两个句子的词向量,LayerNorm会分别对每个句子的所有词向量进行归一化,保持句子内部的分布一致性。
选择建议:
- 若数据批次稳定且特征独立性较强(如图像像素),优先使用
BatchNorm1d; - 若输入结构动态变化或需样本独立处理(如文本序列),选择
LayerNorm。
由小艺AI生成<xiaoyi.huawei.com>
nn.functional.normalize
nn.functional.normalize 是 PyTorch
中用于对张量进行范数归一化的函数。其核心作用是将输入张量沿指定维度缩放,使得该维度上的向量满足特定范数(如
L2 范数)的标准化。以下是其功能详解与应用场景分析:
一、功能原理
范数计算对输入张量沿指定维度(
dim参数)计算范数,默认使用 L2 范数(可通过p参数切换为 L1、无穷范数等)。例如,对形状为(B, C)的张量沿dim=1归一化时,每个样本的特征向量会被缩放为 L2 范数为 1 的单位向量。归一化公式 数学表达式为:
\[ v_{\text{normalized}} = \frac{v}{\max(\|v\|_p, \epsilon)} \]
其中,
\[ \epsilon \]
是防止除零的小常数(默认
1e-12)。
二、参数解析
input: 输入张量,支持任意维度。p: 范数类型,默认为 2(L2 范数),可选 1(L1)、float('inf')(无穷范数)等。dim: 归一化维度,例如dim=1表示对特征维度归一化。eps: 极小值,避免分母为零。
三、典型应用场景
特征向量标准化在对比学习或相似度计算中,将特征向量归一化为单位长度,使点积直接等价于余弦相似度,提升计算效率。
1
embeddings = nn.functional.normalize(embeddings, p=2, dim=1) # 形状 (B, 512) → 每行L2范数为1
注意力权重归一化在注意力机制中,对注意力分数沿特定维度归一化,确保权重和为 1(类似 Softmax,但使用 L1 范数):
1
attention_scores = nn.functional.normalize(attention_scores, p=1, dim=-1)
梯度稳定 在训练过程中对中间特征进行归一化,防止梯度爆炸或消失(需注意与
BatchNorm的区别)。
四、与 BatchNorm 的区别
| 特性 | nn.functional.normalize |
nn.BatchNorm1d |
|---|---|---|
| 是否可学习参数 | 无 | 有(均值、方差、缩放因子) |
| 归一化方式 | 基于瞬时计算的范数 | 基于批次统计的均值和方差 |
| 应用场景 | 静态标准化(如嵌入向量) | 动态适应数据分布(训练阶段依赖批次) |
五、代码示例
1 | import torch |
六、注意事项
- 梯度影响归一化操作会改变张量数值范围,反向传播时需注意梯度计算是否受影响(通常无问题,因归一化是线性缩放)。
- 与 Softmax 的对比
Softmax输出概率分布,归一化依赖指数运算;normalize更灵活,支持任意范数,但无概率解释性。
通过灵活选择范数和维度,nn.functional.normalize
可广泛用于特征工程、注意力机制和模型优化等场景,是 PyTorch
中实现标准化的重要工具。
由小艺AI生成<xiaoyi.huawei.com>
torch.einsum
torch.einsum 函数详解
torch.einsum 是 PyTorch
中一个强大的函数,它实现了爱因斯坦求和约定(Einstein Summation
Convention),可以用简洁的表示法执行各种张量运算。在 SITS-MoCo 的
builder.py
文件中,这个函数被用于计算特征向量之间的相似度。
torch.einsum 基本原理
爱因斯坦求和约定是一种表示张量运算的简洁方法,它使用下标来表示张量的维度,并通过下标的重复来表示求和操作。在
PyTorch 中,torch.einsum 函数的基本语法是:
1 | torch.einsum(equation, operands) |
其中:
equation是一个字符串,表示运算的规则operands是参与运算的张量列表
'nc,nc->n' 的含义
在代码中的这一行:
1 | l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1) |
'nc,nc->n' 的含义是:
- 第一个张量
q的形状是[n,c],其中n表示批次大小(512),c表示特征维度(128) - 第二个张量
k的形状也是[n,c] ->n表示输出张量的形状是[n]
这个操作实际上是在计算每对对应样本之间的点积:
- 对于每个样本
i,计算q[i]和k[i]的点积 - 结果是一个长度为
n的向量,每个元素表示对应位置的样本对的相似度
用数学表达式表示就是:
\[ \text{result}[i] = \sum_{j=0}^{c-1} q[i,j] \times k[i,j] \]
这实际上是计算了正样本对(同一个时间序列的两种不同数据增强版本)之间的相似度。
'nc,ck->nk' 的含义
在代码中的这一行:
1 | l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()]) |
'nc,ck->nk' 的含义是:
- 第一个张量
q的形状是[n,c],其中n表示批次大小(512),c表示特征维度(128) - 第二个张量
self.queue的形状是[c,k],其中c是特征维度(128),k是队列大小(65536) ->nk表示输出张量的形状是[n,k]
这个操作实际上是在计算矩阵乘法:
- 将形状为
[n,c]的矩阵q与形状为[c,k]的矩阵self.queue相乘 - 结果是一个形状为
[n,k]的矩阵,表示当前批次中的每个样本与队列中所有样本的相似度
用数学表达式表示就是:
\[ \text{result}[i,j] = \sum_{l=0}^{c-1} q[i,l] \times \text{queue}[l,j] \]
这实际上是计算了负样本对(当前批次的样本与历史批次中的所有样本)之间的相似度。
在 MoCo 中的应用
在 MoCo 框架中,这两个 einsum 操作的目的是:
l_pos:计算正样本对的相似度,即同一个时间序列的两种不同数据增强版本之间的相似度l_neg:计算负样本对的相似度,即当前批次的样本与队列中存储的历史样本之间的相似度
通过最大化正样本对的相似度和最小化负样本对的相似度,模型能够学习到时间序列数据的有效表示,这是对比学习的核心思想。
总结来说,torch.einsum
函数在这里提供了一种简洁而高效的方式来计算特征向量之间的相似度,是 MoCo
对比学习框架的关键组成部分。
当前模型请求量过大,请求排队约 1 位,请稍候或切换至其他模型问答体验更流畅。数据增强
方法一:
图像增强
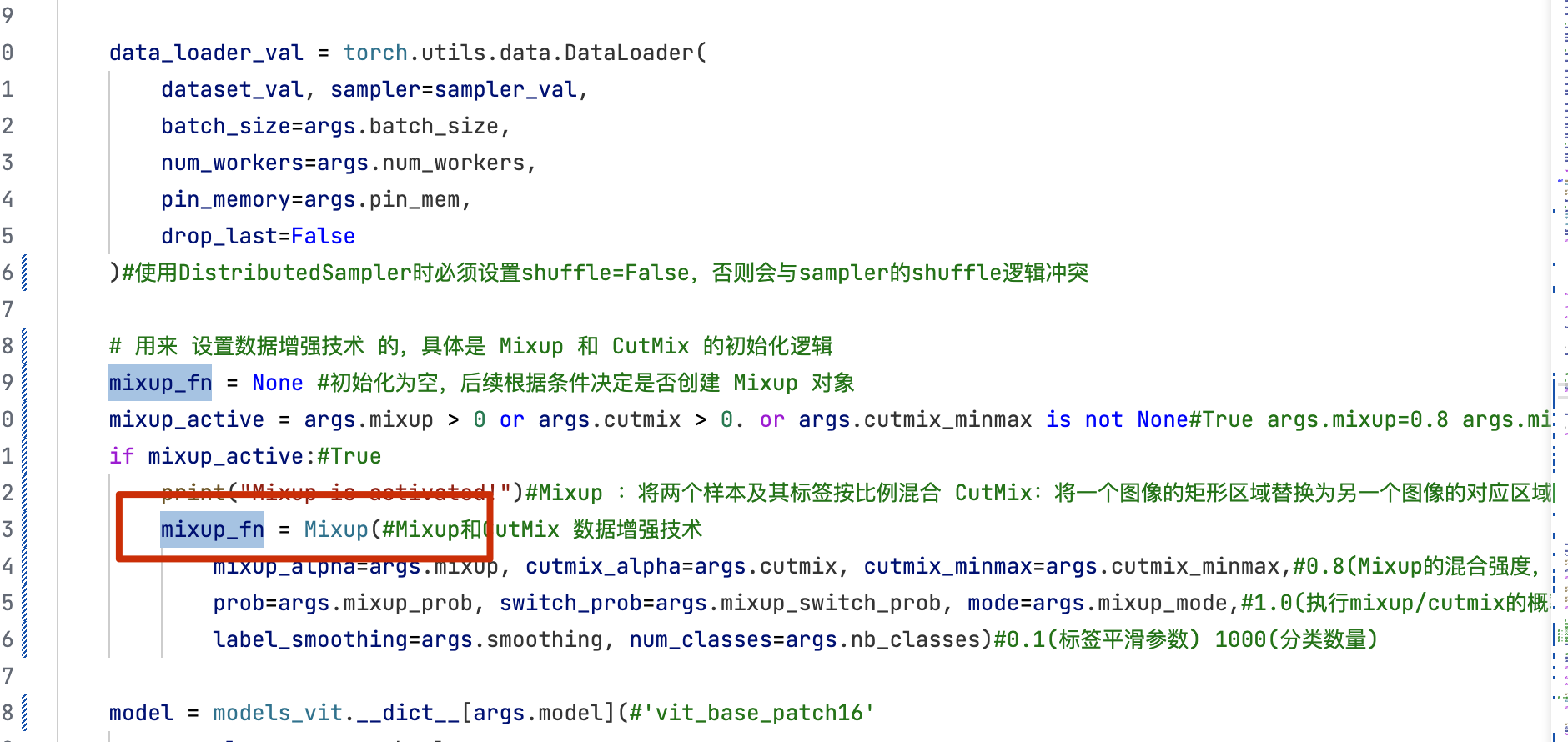
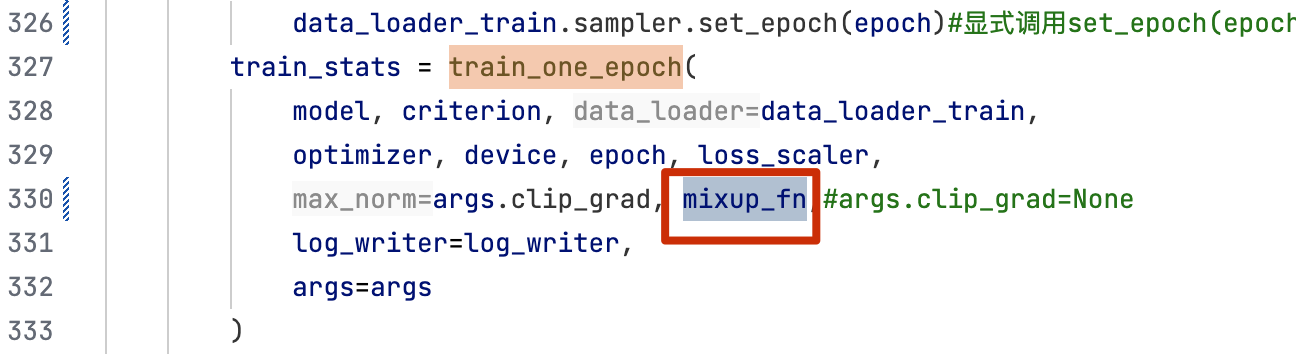
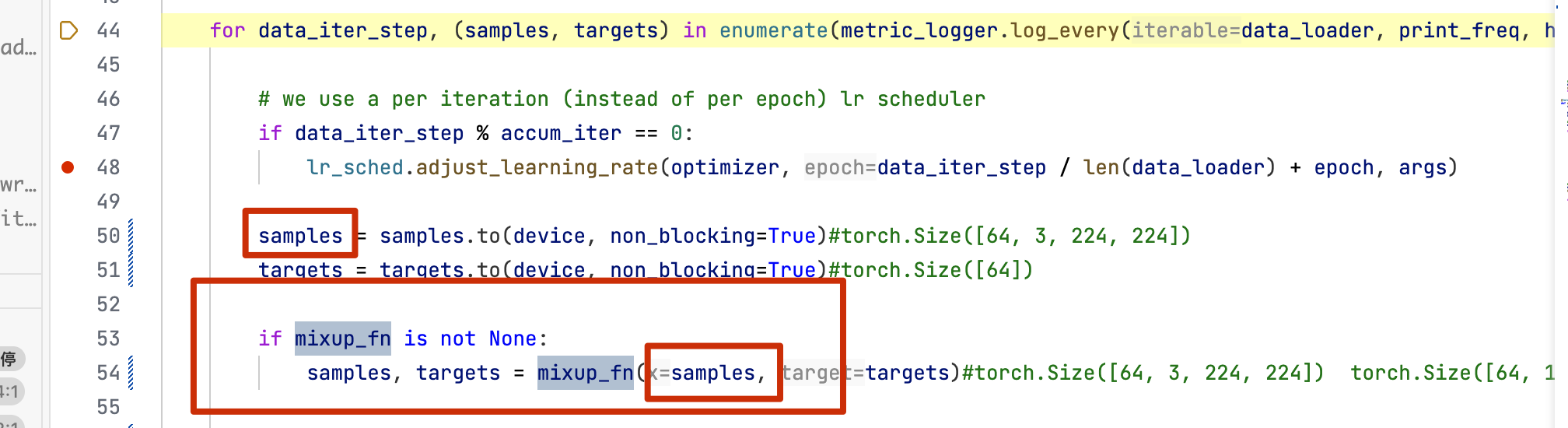
torch.mean
1 | import torch |
optim_factory.add_weight_decay
在PyTorch中添加权重衰减(weight decay)到模型参数的
权重衰减是一种正则化技术,用于防止模型过拟合。具体来说,它通过在损失函数中添加一个与模型参数大小成比例的项来实现。
实现原理
- 获取模型参数 :
model_without_ddp是一个没有分布式数据并行(Distributed Data Parallel, DDP)包装的模型实例。optim_factory是一个工厂类,用于创建优化器。 - 添加权重衰减 :
add_weight_decay方法遍历模型的所有参数,并根据给定的权重衰减系数(args.weight_decay)对参数进行衰减处理。具体来说,它会将权重衰减项添加到每个参数的梯度中。
用途
权重衰减的主要用途是防止模型在训练过程中过度拟合训练数据,从而提高模型在测试数据上的泛化能力。
注意事项
- 权重衰减系数 :
args.weight_decay是一个超参数,需要根据具体任务和数据集进行调整。过高的权重衰减系数可能会导致模型欠拟合,而过低的权重衰减系数可能会导致模型过拟合。 - 参数选择 :
add_weight_decay方法会处理模型的所有参数,包括可训练参数和不可训练参数。如果只想对可训练参数进行权重衰减,可以在调用该方法之前先过滤掉不可训练参数。 - 优化器配置 :在调用
add_weight_decay方法之后,需要将返回的参数组(param_groups)传递给优化器,以便在训练过程中应用权重衰减。
1 | # 假设已经定义了模型和优化器工厂 |
原理
权重衰减通过在损失函数中添加一个与模型参数大小成比例的项来实现。具体来说,对于给定的损失函数
L 和模型参数 w,权重衰减后的损失函数为:
1 | L(w) + λ * ||w||^2 |
其中,λ 是权重衰减系数,||w||^2
是模型参数的 L2 范数。L2 范数是模型参数的平方和,即:
1 | ||w||^2 = w1^2 + w2^2 + ... + wn^2 |
优点
- 防止过拟合:权重衰减通过限制模型参数的大小,使得模型更加简单,从而减少过拟合的风险。
- 提高泛化能力:权重衰减有助于模型在测试数据上获得更好的性能。
缺点
- 可能降低训练速度:权重衰减会增加损失函数的难度,使得优化器在寻找最优解时需要更多的迭代次数,从而降低训练速度。
应用
权重衰减广泛应用于各种机器学习模型中,包括神经网络、支持向量机等。在深度学习中,权重衰减通常与正则化技术(如 L1 正则化)结合使用,以进一步提高模型的泛化能力。
tf.one_hot
tf.one_hot 是 TensorFlow
中的一个函数,用于将输入的索引值转换为独热编码(One-Hot
Encoding)的张量。
独热编码是一种将类别变量转换为二进制向量的编码方式,其中只有一个元素为 1 ,其余元素为 0 。
以下是 tf.one_hot 函数的一般用法:
1 | import tensorflow as tf |
在上述示例中,indices
是要编码的索引值列表,depth
表示编码的维度(即类别数量)。
例如,对于索引值 0 ,在维度为 4
的编码中,得到的独热编码为 [1, 0, 0, 0] ;对于索引值
2 ,得到的编码为 [0, 0, 1, 0] 。
tf.one_hot
常用于将分类标签转换为适合神经网络输入的形式,方便模型进行处理和计算。
上述代码中,indices = [0, 2, 1, 3] 且
depth = 4 ,使用 tf.one_hot
函数进行独热编码后的输出结果应该是:
1 | [[1 0 0 0] |
即索引为 0 的位置编码为 [1, 0, 0, 0] ,索引为 2
的位置编码为 [0, 0, 1, 0] ,索引为 1 的位置编码为
[0, 1, 0, 0] ,索引为 3 的位置编码为
[0, 0, 0, 1] 。
self.critic_net.parameters()
self.critic_net.parameters() 通常是在 Python
的深度学习框架(如 PyTorch)中使用的代码。
critic_net
可能是您定义的一个神经网络模型(例如,用于评估或批评某些数据的模型)。
parameters()
方法返回模型中的可学习参数,这些参数通常是权重(weights)和偏置(biases)。
例如,如果 critic_net
是一个简单的全连接神经网络,那么通过
self.critic_net.parameters()
您将获取到该网络中所有层的权重和偏置的迭代器。
您可以使用这个返回值来进行一些操作,比如:
在优化器中使用它来进行参数的更新,例如:
1
optimizer = torch.optim.SGD(self.critic_net.parameters(), lr=0.01)
对参数进行一些统计或分析,比如计算参数的数量、查看参数的值等。
总之,self.critic_net.parameters()
为您提供了对模型可学习参数的访问,以便进行各种与模型训练和优化相关的操作。
self.optimizer.zero_grad()
self.optimizer.zero_grad()
通常用于将模型参数的梯度清零。
当进行反向传播计算梯度后,如果不将梯度清零,那么在后续的迭代中,新计算的梯度会与之前的梯度累加。这会导致梯度计算的错误,影响模型的训练效果
loss.backward(retain_graph=True)
在深度学习中,loss.backward(retain_graph=True)
用于计算损失函数 loss 关于模型参数的梯度,同时通过设置
retain_graph=True 来保留计算图。
通常,在进行一次反向传播计算梯度后,计算图会被释放以节省内存。但当您需要多次对同一计算图执行反向传播时,就需要设置
retain_graph=True 。
例如,如果您在一个循环中多次计算梯度并更新参数,像下面这样:
1 | for _ in range(num_iterations): |
在上述示例中,由于在循环内多次执行反向传播,所以需要保留计算图,以便下一次迭代能够再次基于相同的计算图计算梯度。
如果不设置 retain_graph=True ,在第二次执行
loss.backward() 时会报错,因为计算图已经被释放。
需要注意的是,一直保留计算图会占用较多内存,所以在不需要多次使用计算图时,应避免设置
retain_graph=True ,以节省内存资源。
在 PyTorch 中,retain_graph=True
的作用是在执行反向传播(backward)后保留计算图。
PyTorch
采用动态图机制,默认情况下,每次反向传播之后都会释放计算图以节省内存。然而,当需要对同一个计算图进行多次反向传播时,就需要设置
retain_graph=True。
例如,假设有一个输入 x,经过一些计算得到
y,然后有两个输出 output_1 和
output_2,都需要对其执行反向传播。如果在第一次对
output_1 执行 backward 时没有设置
retain_graph=True,那么在执行完后计算图就会被释放。当再对
output_2 执行 backward
时,由于计算图已经不存在,就会引发错误。
通过设置 retain_graph=True,可以保留中间参数,使得多次
backward 之间不会相互影响。例如:
1 | loss1.backward(retain_graph=True) # 第一次 backward,保留计算图 |
需要注意的是,一直保留计算图会占用较多内存,所以在不需要多次使用计算图时,应避免设置
retain_graph=True,以节省内存资源。
另外,create_graph
参数用于创建导数计算图,允许进行高阶导数的计算;而
grad_tensors
可用于设置多梯度的权重,当有多个损失函数需要计算梯度时,可以设置各个损失之间权重的比例。
如何判断是否需要多次使用计算图?
判断是否需要多次使用计算图,主要考虑以下几个方面:
- 模型的结构和需求:如果你的模型在一次前向传播后,需要对不同的输出或中间结果进行多次反向传播来计算梯度,以实现不同的目的,例如优化不同的部分或计算多个相关的梯度,那么就可能需要多次使用计算图。
- 是否涉及多个相关的损失函数:当存在多个损失函数,且需要分别或同时根据这些损失函数计算梯度并更新参数时,通常需要多次使用计算图。
- 循环或迭代的操作:在某些情况下,可能会在一个循环或迭代中多次执行类似的计算和反向传播操作。例如,在强化学习中,可能需要在每个时间步都进行前向传播和反向传播。
- 中间结果的重用:如果在计算过程中需要多次访问或使用某些中间结果的梯度,那么就需要保留计算图以进行多次反向传播。
例如,如果你有一个神经网络模型,其中包含多个子模块,每个子模块都有自己的损失,并且你希望分别根据这些子模块的损失来更新它们的参数,那么就需要多次使用计算图,对每个子模块的损失进行单独的反向传播。
又或者在训练过程中,你可能想要尝试不同的优化策略或超参数,需要在同一次前向传播后,多次计算梯度并更新参数,来比较不同策略或参数的效果,这也需要多次使用计算图。
另外,一些复杂的模型结构或自定义的计算流程可能会导致需要多次使用计算图的情况。但需注意,一直保留计算图会占用较多内存,所以在不需要多次使用计算图时,应避免设置
retain_graph=True ,以节省内存资源。
如果你不确定是否需要多次使用计算图,可以先尝试在不保留计算图的情况下(即不设置
retain_graph=True )运行代码,观察是否会出现报错“trying to
backward through the graph a second time, but the buffers have already
been freed”。如果出现该报错,且确实需要进行多次反向传播,那么就需要设置
retain_graph=True
。同时,为了避免内存过度占用,在完成所有需要的反向传播后,应及时释放不再使用的计算图和相关数据。
transformer 位置嵌入
tf.reduce_mean
tf.reduce_mean 是 TensorFlow
中的一个函数,用于计算张量在指定维度上的平均值。
以下是一个示例:
1 | import tensorflow as tf |
在上述示例中:
- 当不指定
axis参数时,tf.reduce_mean(tensor)计算张量tensor中所有元素的平均值。 tf.reduce_mean(tensor, axis=1)计算每一行的平均值,得到一个长度为行数的张量。tf.reduce_mean(tensor, axis=0)计算每一列的平均值,得到一个长度为列数的张量。
例如,对于上述示例中的张量 [[1, 2, 3], [4, 5, 6]] :
- 所有元素的平均值为
(1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5。 - 每一行的平均值分别为
(1 + 2 + 3) / 3 = 2和(4 + 5 + 6) / 3 = 5。 - 每一列的平均值分别为
(1 + 4) / 2 = 2.5、(2 + 5) / 2 = 3.5和(3 + 6) / 2 = 4.5。
tf.placeholder
用于表示强化学习或神经网络中的状态输入
1 | with tf.name_scope('S'):#状态 |
- tf.name_scope('S')
这行代码使用 TensorFlow 的 tf.name_scope 创建一个命名空间 S。命名空间在 TensorFlow 中用于组织图中的节点,使其更具可读性和结构化。在 TensorBoard 中查看图时,可以更清晰地看到节点的组织结构。
- tf.placeholder(tf.float32, shape=[None, state_dim], name='s')
这行代码定义了一个占位符 S。占位符在 TensorFlow 中用于在执行图时提供输入数据。这里的占位符有以下几个参数:
tf.float32:占位符的数据类型是 32 位浮点数。
shape=[None, state_dim]:占位符的形状。shape 参数定义了输入数据的维度:
None 表示这个维度可以是任意长度,通常用于批次(batch)的大小。使用 None 是因为在实际运行时,批次的大小可能会有所不同。
state_dim 表示状态的维度。这是一个整数,定义了每个状态的特征数量。在强化学习中,状态通常是一个向量,其长度由具体的环境或问题决定。
name='s':给占位符命名为 's'。这个名字在构建和调试图时有助于识别。

tf.variable_scope
tf.variable_scope 是 TensorFlow
中用于管理变量作用域的一个重要工具。它帮助组织和复用变量,特别是在构建复杂的神经网络时
1. 什么是
tf.variable_scope?
tf.variable_scope
提供了一种机制来创建和管理变量范围(scope),这对变量进行命名和复用非常有帮助。通过使用变量范围,可以确保变量命名的一致性和避免命名冲突。
2. 为什么使用
tf.variable_scope?
- 组织变量:可以将相关的变量组织在一起,使代码更具可读性和结构性。
- 复用变量:在共享参数的模型(如共享权重的神经网络层)中,复用变量非常重要。
- 命名管理:自动处理变量命名,避免命名冲突。
3. 如何使用
tf.variable_scope?
使用 tf.variable_scope
创建一个新的变量作用域,可以在该作用域内定义和复用变量。
示例 1:创建变量作用域
1 | with tf.variable_scope('scope1'): |
在这个例子中,var1 和 var2
是在不同的变量作用域中创建的,尽管它们的名字相同,但在图中它们是不同的变量,分别命名为
scope1/var 和 scope2/var。
示例 2:复用变量
1 | with tf.variable_scope('scope', reuse=tf.AUTO_REUSE): |
在这个例子中,var2 复用了 var1
的变量。通过设置
reuse=True,确保在相同的作用域内复用已经存在的变量。
4.
tf.get_variable 和 tf.Variable 的区别
tf.get_variable:用于创建或获取变量,通常与tf.variable_scope一起使用。它支持变量复用机制。tf.Variable:直接创建新变量,不支持复用机制。
示例 3:使用
tf.get_variable 和 tf.Variable
1 | with tf.variable_scope('scope1'): |
在这个例子中,var1 是通过 tf.get_variable
创建的,支持复用机制,而 var2 是通过
tf.Variable 创建的,不支持复用。
5. 总结
tf.variable_scope 是 TensorFlow
中用于管理变量作用域的工具,帮助组织和复用变量,提供了一种结构化和高效的变量管理方式。通过合理使用变量作用域,可以避免命名冲突,实现变量复用,特别是在构建共享参数的复杂神经网络时非常有用。
tf.Session
tf.Session 是 TensorFlow 1.x
中一个重要的类,用于执行定义好的计算图(computation graph)。在
TensorFlow 2.x 中,tf.Session 被逐渐弃用,更多地采用了
Eager Execution 模式,但了解 tf.Session
对于维护和理解旧代码还是非常重要的。以下是对 tf.Session
的详细解释及其使用方法。
1. 什么是 tf.Session?
tf.Session 提供了一个运行 TensorFlow 操作的环境。它管理
TensorFlow 运行时的所有资源,包括变量的内存分配、执行设备的选择等。
2. 为什么需要
tf.Session?
在 TensorFlow 1.x
中,计算图的定义和执行是分开的。你首先定义一个计算图,然后在
tf.Session 中执行它。tf.Session
提供了以下功能:
- 控制和管理资源:例如内存、线程等。
- 分配计算设备:决定在 CPU 还是 GPU 上执行操作。
- 执行计算图:运行图中的操作,获取结果。
3. 如何使用 tf.Session?
示例 1:基本使用
1 | import tensorflow as tf |
在这个例子中,首先定义了一个简单的计算图,然后创建一个
tf.Session 来运行这个图,并获取结果。
示例 2:使用
tf.placeholder 和 feed_dict
1 | import tensorflow as tf |
在这个例子中,使用 tf.placeholder
定义了占位符,可以在运行时通过 feed_dict 提供输入数据。
示例 3:管理变量
1 | import tensorflow as tf |
在这个例子中,定义了一个变量,并在会话中运行初始化操作来分配和初始化变量。
4. TensorFlow 2.x 中的变化
在 TensorFlow 2.x 中,引入了 Eager Execution,默认情况下无需显式创建会话,可以直接执行操作。例如:
1 | import tensorflow as tf |
5. 总结
tf.Session 是 TensorFlow 1.x
中用于执行计算图的核心工具,帮助管理和控制资源,执行计算操作。在
TensorFlow 2.x 中,虽然 tf.Session
被弃用,但理解它的工作机制对于维护旧代码和理解 TensorFlow
的运行原理仍然非常重要。
tf.random_normal_initializer
这是 TensorFlow 提供的一个初始化器,用于从正态分布(高斯分布)中随机抽取样本来初始化变量。
背景知识
在神经网络中,权重和偏置的初始化对模型的收敛速度和效果有很大影响。TensorFlow 提供了多种初始化器来帮助我们初始化这些变量。
1 | init_w = tf.random_normal_initializer(0., 0.3) |
参数解释 :
- 第一个参数
0.:表示正态分布的均值(mean)。在这里,均值被设置为0。 - 第二个参数
0.3:表示正态分布的标准差(standard deviation)。在这里,标准差被设置为0.3。 因此,tf.random_normal_initializer(0., 0.3)表示使用均值为0、标准差为0.3的正态分布来初始化变量。
实例说明
以下是一个简单的示例,展示如何使用这个初始化器来初始化一个 TensorFlow 变量:
1 | import tensorflow as tf |
解释这个示例
- 定义初始化器
:
init_w = tf.random_normal_initializer(0., 0.3)定义了一个初始化器,它会生成均值为0、标准差为0.3的随机数。 - 初始化变量
:
var = tf.Variable(initial_value=init_w(shape=[2, 3], dtype=tf.float32))使用这个初始化器来初始化一个形状为[2, 3]的变量。 - 初始化全局变量
:
tf.compat.v1.global_variables_initializer()用于初始化所有的 TensorFlow 变量。 - 运行会话 :创建并运行一个 TensorFlow 会话以查看变量的值。
tf.compat.v1.global_variables_initializer
tf.compat.v1.global_variables_initializer 是 TensorFlow
1.x 中的一个函数,用于初始化所有的全局变量。在 TensorFlow 2.x
中,这个函数被包括在 compat.v1 模块中,以便兼容旧代码。
作用
tf.compat.v1.global_variables_initializer()
函数会创建一个操作(operation),这个操作会初始化 TensorFlow
图中的所有全局变量。执行这个操作能够将所有变量赋值为它们的初始值。
变量初始化的重要性
在使用 TensorFlow 构建和训练模型时,变量(如权重和偏置)需要先被初始化,然后才能在计算图中使用。未初始化的变量在使用时会导致错误。
使用示例
下面是一个简单的示例,展示了如何使用
tf.compat.v1.global_variables_initializer()
来初始化变量:
1 | import tensorflow as tf |
解释这个示例
创建变量:我们创建了两个变量
var1和var2,它们的初始值是从正态分布中随机抽取的。创建初始化操作:使用
tf.compat.v1.global_variables_initializer()创建一个初始化操作init_op。运行会话:
- 使用
with tf.compat.v1.Session() as sess:创建一个 TensorFlow 会话。 - 使用
sess.run(init_op)来运行初始化操作,初始化所有变量。 - 之后,通过
sess.run(var1)和sess.run(var2)来查看变量的值。
- 使用
TensorFlow 2.x 的变化
在 TensorFlow 2.x 中,变量的初始化通常由更高级别的 API(如
Keras)自动处理。直接使用
tf.compat.v1.global_variables_initializer()
的情况较少见,除非是在兼容旧代码或使用低级别 API 时。
以下是 TensorFlow 2.x 的一个简单示例:
1 | import tensorflow as tf |
总结
tf.compat.v1.global_variables_initializer()
是用于初始化所有全局变量的函数。在 TensorFlow 2.x 中,通常通过更高级别的
API 处理变量的初始化,但在需要兼容 TensorFlow 1.x
代码时,tf.compat.v1.global_variables_initializer()
仍然非常有用。通过初始化变量,确保在计算图中使用这些变量时不会遇到未初始化变量的错误。
tf.constant_initializer
tf.constant_initializer 是 TensorFlow
中的一个初始化器,用于创建一个常量初始化器对象,该对象用于将变量初始化为指定的常量值。
使用方法
1 | initializer = tf.constant_initializer(value) |
其中:
value是要初始化的常量值。
示例
以下是一个简单的示例,展示如何使用
tf.constant_initializer 来初始化一个 TensorFlow
变量为常量值:
1 | import tensorflow as tf |
解释这个示例
创建初始化器:使用
tf.constant_initializer(42.0)创建一个常量初始化器,它会将变量初始化为常量值42.0。初始化变量:使用
initializer(shape=[2, 3])创建一个形状为[2, 3]的变量,并使用常量初始化器初始化它。运行会话:
- 使用
tf.compat.v1.global_variables_initializer()初始化所有变量。 - 使用
sess.run(var)在会话中运行并打印变量的值,输出将会是一个形状为[2, 3]的数组,其所有元素都是42.0。
- 使用
应用场景
- 固定初始化值:当你希望将所有权重或偏置初始化为固定的常量值时,可以使用
tf.constant_initializer。 - 保证初始化的一致性:有时在调试和开发过程中,需要确保变量被初始化为固定的常量,以便进行稳定性检查和测试。
TensorFlow 2.x 的变化
在 TensorFlow 2.x 中,变量的初始化通常由更高级别的 API(如
Keras)自动处理。直接使用 tf.constant_initializer
的情况较少见,除非是在兼容旧代码或使用低级别 API 时。
总结
tf.constant_initializer 是 TensorFlow
中的一个初始化器,用于将变量初始化为指定的常量值。通过设置常量值,可以确保在构建和训练神经网络时,某些变量始终具有固定的初始值。
tf.layers.dense
tf.layers.dense 是 TensorFlow
提供的一个高级API,用于创建全连接层。它自动创建并管理权重变量(kernel)和偏置变量(bias),并且可以通过参数来控制激活函数、初始化器、层名称等。这样可以简化神经网络的构建过程,并提供了一致性的接口。
示例解释
1 | import tensorflow as tf |
这段代码的作用是在输入张量 s 上创建一个具有 30
个神经元、ReLU
激活函数的全连接层,使用指定的权重和偏置初始化器,并指定该层为可训练的。这样,TensorFlow
将自动处理该层的变量初始化和管理,使得神经网络的搭建更加高效和便捷。
上面30 个神经元的含义
神经网络中的“神经元”是指一个计算单元,它接收输入、应用权重和偏置,并通过激活函数产生输出。在全连接层(dense layer)中,神经元的数量决定了该层的输出维度。
在代码
net = tf.layers.dense(s, 30, activation=tf.nn.relu, kernel_initializer=init_w, bias_initializer=init_b, name='l1', trainable=trainable)
中,指定了这一层有 30 个神经元。具体来说:
- 输入张量 :假设输入张量
s的形状为[batch_size, input_dim],其中batch_size是批次大小(每次训练或推理使用的样本数量),input_dim是输入特征的数量。 - 神经元的作用 :每个神经元都接收输入张量
s的所有特征,将这些特征与它自身的权重(weights)相乘,然后加上一个偏置(bias),再通过激活函数(如 ReLU)计算输出。 - 输出维度 :具有 30 个神经元意味着输出张量的形状将是
[batch_size, 30]。也就是说,每个输入样本将被转换为一个 30 维的输出向量。
详细步骤
- 权重矩阵 :如果输入张量
s的形状为[batch_size, input_dim],则权重矩阵W的形状为[input_dim, 30]。 - 计算加权和 :每个神经元计算加权和
z = W*x + b,其中x是输入特征,W是权重,b是偏置。 - 应用激活函数 :计算出加权和
z后,应用激活函数a = activation(z)。在这个例子中,激活函数是 ReLU,即a = max(0, z)。 - 输出张量 :最终,每个输入样本被转换为一个 30
维的输出向量,所有样本组成的输出张量形状为
[batch_size, 30]。
举例说明
假设我们有一个输入张量 s,形状为
[batch_size=2, input_dim=5]:
我们定义一个具有 30 个神经元的全连接层:
1 | net = tf.layers.dense(s, 30, activation=tf.nn.relu) |
输入张量 s 的形状是 [2, 5],经过具有 30
个神经元的全连接层后,输出张量 net 的形状将是
[2, 30]。每个输入样本(2 个样本)被转换为一个 30
维的输出向量。
总之,具有 30 个神经元意味着这一层的输出维度是 30,每个输入样本将被转化为一个 30 维的向量。这有助于神经网络在不同层之间传递和处理信息,提取和学习更复杂的特征。
tf.multiply :
tf.multiply是 TensorFlow 的一个操作,用于逐元素相乘。它的输入是两个张量,输出是这两个张量对应位置元素相乘的结果。
tf.get_collection
tf.get_collection 是 TensorFlow
中用于获取一个集合中的所有元素的函数。集合在 TensorFlow
中是一种组织和管理变量、操作等对象的方式,可以通过集合来方便地访问和操作这些对象。
函数原型
1 | tf.get_collection(key, scope=None) |
参数
key:- 表示要获取的集合的键(名称),是一个字符串。
- TensorFlow 中有一些预定义的集合键,例如
tf.GraphKeys.GLOBAL_VARIABLES、tf.GraphKeys.TRAINABLE_VARIABLES等。
scope(可选):- 表示要获取的集合中元素的作用域(scope)。如果指定了
scope,则只返回该作用域内的元素。
- 表示要获取的集合中元素的作用域(scope)。如果指定了
返回值
返回与 key
对应的集合中的所有元素,通常是一个列表。如果集合不存在,返回空列表。
举例说明
假设我们在构建神经网络时,将一些变量添加到集合中,然后在训练或评估时需要获取这些变量,可以使用
tf.get_collection。
示例代码
1 | import tensorflow as tf |
预定义集合键
TensorFlow 提供了一些常用的集合键,方便用户管理变量和操作:
tf.GraphKeys.GLOBAL_VARIABLES:所有全局变量。tf.GraphKeys.TRAINABLE_VARIABLES:所有可训练的变量。tf.GraphKeys.SUMMARIES:所有摘要操作。tf.GraphKeys.UPDATE_OPS:所有需要在训练时执行的更新操作。
在实际应用中的使用
获取所有可训练变量
在训练神经网络时,我们通常需要获取所有可训练的变量,例如在优化器中:
1 | trainable_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES) |
获取特定作用域内的变量
我们还可以使用 scope 参数来获取特定作用域内的变量:
1 | with tf.variable_scope('layer1'): |
总结
tf.get_collection
是一个强大的函数,允许用户根据集合键和作用域来获取 TensorFlow
图中的变量和操作。它在组织和管理复杂模型中的变量和操作时非常有用,尤其是在训练、保存和恢复模型时。通过合理使用集合和
tf.get_collection,可以使代码更加清晰和易于维护。
tf.stop_gradient
tf.stop_gradient 是 TensorFlow
中用于阻止梯度反向传播的操作。它返回一个与输入张量具有相同内容的新张量,但在计算梯度时会被视为常量。换句话说,tf.stop_gradient
可以用来“截断”梯度的传播,这在某些情况下(例如实现某些特殊的梯度更新规则或避免某些变量的梯度更新)非常有用。
函数原型
1 | tf.stop_gradient( |
参数
input:输入张量。name(可选):操作名。
返回值
返回一个与输入张量具有相同内容的新张量,但在反向传播过程中,该张量的梯度将被视为零。
使用示例
示例1:简单示例
1 | import tensorflow as tf |
在这个例子中,y_no_grad 是通过
tf.stop_gradient 创建的,因此在计算 loss
的梯度时,y_no_grad 不会对 x
的梯度产生影响。最终结果是 gradients 只包含 x
的梯度,即 1,而不是 y = x * 2 导致的 2。
示例2:在神经网络中的应用
在一些强化学习算法中,我们可能希望通过停止梯度来实现某些特殊的策略。例如,在
DDPG 算法中,actor 网络的输出动作传递给 critic 网络,但我们不希望通过
critic 网络更新 actor 网络的参数,可以使用 tf.stop_gradient
实现这一点。
1 | import tensorflow as tf |
在这个例子中,tf.stop_gradient(a) 确保了
critic_network 的梯度不会影响 actor_network
的参数更新。
总结
tf.stop_gradient
是一个非常有用的操作,特别是在需要控制梯度传播路径或实现自定义梯度更新规则时。通过合理使用
tf.stop_gradient,可以更灵活地设计和训练复杂的模型。
软替换代码
代码理解:
1 | self.soft_replace = [tf.assign(t, (1 - self.replacement['tau']) * t + self.replacement['tau'] * e) |
这一行代码的作用是实现软替换(soft replacement),用来逐步更新目标网络的参数,使其接近评估网络的参数。在强化学习中,软替换是一种常见的参数更新策略,常用于深度确定性策略梯度(DDPG)等算法。
让我们逐步解析这段代码:
zip(self.t_params, self.e_params):self.t_params包含目标网络的所有参数。self.e_params包含评估网络的所有参数。zip函数将这两个参数列表配对,使得每对包含一个目标网络的参数和一个评估网络的参数。
列表推导式:
- 列表推导式用于生成一个包含多个 TensorFlow
操作的列表。在这里,每个操作都是一个
tf.assign操作,用于更新目标网络的参数。
- 列表推导式用于生成一个包含多个 TensorFlow
操作的列表。在这里,每个操作都是一个
tf.assign:tf.assign是 TensorFlow 中用于更新变量值的操作。它接受两个参数:要更新的变量和新的值。t是目标网络的参数,e是评估网络的参数。
软更新公式:
1
(1 - self.replacement['tau']) * t + self.replacement['tau'] * e
self.replacement['tau']是软更新的速率,通常是一个小值(如 0.01)。它控制了目标网络参数向评估网络参数靠拢的速度。(1 - self.replacement['tau']) * t保留了目标网络参数的大部分值。self.replacement['tau'] * e引入了一小部分评估网络参数的值。- 通过这种加权平均的方式,目标网络参数逐步向评估网络参数靠拢,但不会立即完全相同。
生成软替换操作列表:
- 对于每一对目标网络参数
t和评估网络参数e,生成一个tf.assign操作,将目标网络参数更新为加权平均后的值。 self.soft_replace最终是一个包含所有这些tf.assign操作的列表。
- 对于每一对目标网络参数
软替换的具体作用
在强化学习算法中,目标网络和评估网络的更新策略对算法的稳定性至关重要。软替换通过逐步更新目标网络的参数,可以减少训练过程中的振荡和不稳定性。相对于硬替换(每隔一段时间直接将评估网络的参数复制到目标网络),软替换更为平滑和稳定,有助于提高算法的训练效果。
示例
假设评估网络和目标网络的参数分别为 e_params = [1, 2, 3]
和 t_params = [4, 5, 6],且
tau = 0.1,则软替换后的目标网络参数计算如下:
1 | new_t_params = [(1 - 0.1) * 4 + 0.1 * 1, (1 - 0.1) * 5 + 0.1 * 2, (1 - 0.1) * 6 + 0.1 * 3] |
每次更新后,目标网络的参数都会逐渐向评估网络的参数靠拢,但不会立即相同,从而实现平滑的参数更新。
硬替换代码
1 | self.t_replace_counter = 0 |
tf.gradients
tf.gradients 是 TensorFlow
中用于计算梯度的函数。它的主要功能是计算某个或某些张量(ys)相对于另一些张量(xs)的导数。
其函数签名如下:
1 | tf.gradients(ys, xs, grad_ys=None, name='gradients', colocate_gradients_with_ops=False, gate_gradients=False, aggregation_method=None, stop_gradients=None) |
参数说明如下:
ys:表示要计算梯度的张量或张量列表。xs:表示要对哪些张量计算梯度的张量或张量列表。grad_ys(可选):也是一个张量或张量列表,用于对ys中的每个元素进行加权。如果未提供,则默认为每个元素都是 1。name(可选):操作的名称。colocate_gradients_with_ops(可选):通常不需要设置。gate_gradients(可选):通常不需要设置。aggregation_method(可选):聚合方法,一般使用默认值即可。stop_gradients(可选):是一个张量或张量列表,用于指定在反向传播中梯度停止的节点。这意味着这些节点的梯度不会再向后传播,就好像它们被明确地断开了一样。
例如,如果 ys 是一个张量,xs
是一个张量列表,那么返回的是一个与 xs
长度相同的列表,其中每个元素是 ys 相对于 xs
中对应张量的导数。
如果 ys 和 xs
都是张量列表,那么它会计算每个 ys 中的张量相对于每个
xs 中的张量的导数,并将结果以适当的方式组合成一个列表。
下面是一个简单的示例,假设有两个变量 w1 和
w2,通过矩阵乘法等操作得到结果 res,然后使用
tf.gradients 计算 res 相对于 w1
和 w2 的梯度:
1 | import tensorflow as tf |
在上述示例中,tf.gradients
返回了一个包含两个梯度张量的列表,分别对应 res 相对于
w1 和 w2 的梯度。
stop_gradients 参数的使用示例如下:
1 | import tensorflow as tf |
在这个例子中,由于使用了 stop_gradients=(a, b),所以
a 和 b
的梯度在计算后不会再向后传播,得到的梯度结果为
(1.0, 1.0),而不是通常情况下的
(3.0, 1.0)。
如何理解stop_gradients
具体来说,对于表达式
pg = tf.gradients(a+b, (a, b), stop_gradients=(a, b)),意味着在计算
a+b 相对于 a 和 b
的梯度时,a 和 b
本身的梯度不会再进一步向后传播。也就是说,a
的梯度不会影响到依赖于 a 的其他操作,b
的梯度也不会影响到依赖于 b 的其他操作。
这在一些情况下是有用的,例如当你不希望某些变量的梯度继续传播,或者想要模拟某些部分的梯度为固定值的情况。通过设置
stop_gradients,可以更灵活地控制梯度的计算和传播。
例如,如果 a 和 b
是神经网络中的某些中间节点,并且你不希望它们的梯度对网络的其他部分产生影响,就可以将它们放入
stop_gradients 中。这样,在反向传播时,就只会计算到
a+b 这一步,而不会将梯度继续传播到 a 和
b 所依赖的其他变量上。
举个简单的例子,假设有如下计算图:c = a + b,d = c * x,如果计算
d 相对于 a 的梯度,正常情况下梯度会从
d 传播到 c,再传播到
a。但如果使用
stop_gradients=(a, b),那么梯度只会传播到
c,而不会再传播到 a 和 b,即
a 和 b
的梯度不会再向后传播。这样可以在一定程度上实现对梯度传播的控制和干预。
需要注意的是,tf.stop_gradient
是在构建图的过程中使用,用来指定停止链式法则的节点;而
stop_gradients 是在构建图之后使用,当程序运行碰到在
stop_gradients
中定义的节点时,均会停止链式法则,进而求得部分偏导。它们的作用都是阻止梯度的进一步传播,但使用的时机略有不同。
grad_ys 参数用于对梯度进行加权,例如:
1 | import tensorflow as tf |
这里的 grad_ys 对 z1 和 z2
的梯度进行了加权,最终得到的梯度结果会相应地受到加权的影响。
在 TensorFlow 2.x 中也可以使用
tf.gradients,但通常更推荐使用 tf.GradientTape
来进行自动求导,它在使用上更加灵活和方便。不过,在某些情况下,仍然可能需要使用
tf.gradients,例如在一些特定的模型架构或代码结构中。但要注意将其放在计算图中使用。如果不在计算图中使用,就需要使用
tf.GradientTape 来替代。
tf.gradients的输入和输出之间的形状的关系
在 TensorFlow 中,tf.gradients()
用于计算梯度。它接受求导的目标值 ys 和自变量
xs,返回的梯度值与 ys 和 xs
张量之间的形状关系如下:
tf.gradients() 返回的结果是一个长度为
len(xs)
的张量列表。--------------这是重点
一般情况下,tf.gradients(self.q, self.a)
的返回值形状应该是与 self.a 的形状相同
如果 ys 是单个张量,那么每个返回的张量表示相应的
xs 元素对 ys 的梯度。如果 ys
是张量列表,那么返回的张量列表中的每个张量是所有 ys
张量对相应 xs 元素的梯度之和。
具体来说,假设 ys = (y1, y2,..., ym)
是一个张量列表,xs = (x1, x2,..., xn)
也是一个张量列表。那么返回的梯度列表中第 i
个张量表示的是所有 y 张量对 xi
的梯度之和,即:
\(\frac{d(y1 + y2 +... + ym)}{dx_i}\)
如果 ys
是单个张量,那么返回的列表中只有一个张量,其形状与 xs
中的元素形状相对应,表示该 ys 张量对每个 xs
元素的梯度。
例如,当 ys = (y1, y2),xs = (x1, x2, x3)
时,返回的梯度结果为 (grad1, grad2, grad3),其中:
grad1表示的是 \(\frac{y1}{x1} + \frac{y2}{x1}\)grad2表示的是 \(\frac{y1}{x2} + \frac{y2}{x2}\)grad3表示的是 \(\frac{y1}{x3} + \frac{y2}{x3}\)
另外,tf.gradients() 还有一个参数
grad_ys,它也是一个张量列表,用于对 ys
中的每个张量进行加权。如果提供了
grad_ys,则计算梯度时会将每个 y 张量乘以对应的
grad_ys 张量后再进行求导。
例如,在上述同样的 ys 和 xs 的情况下,如果
grad_ys = (g1, g2),那么计算的梯度将变为:
grad1表示的是 \(\frac{g1 * y1}{x1} + \frac{g2 * y2}{x1}\)grad2表示的是 \(\frac{g1 * y1}{x2} + \frac{g2 * y2}{x2}\)grad3表示的是 \(\frac{g1 * y1}{x3} + \frac{g2 * y2}{x3}\)
如何理解 grad_ys
grad_ys(可选)是一个张量或张量列表,用于对
ys 中的每个元素进行加权。
当使用 tf.gradients(ys, xs, grad_ys) 时,如果
grad_ys 不为空,就需要使用梯度求导的链式法则来计算相对于
xs 的导数。
假设 grad_ys = (grad_ys1, grad_ys2,..., grad_ysn),其中
n 是 ys
中元素的个数,xs = (x1, x2,..., xm)。那么对于
xs 中的每个元素 xi,其梯度计算方式为:
新的梯度
new_grad(i) = ∂/∂xi = ∂/∂z1 * ∂z1/∂xi + ∂/∂z2 * ∂z2/∂xi +... + ∂/∂zn * ∂zn/∂xi,其中
z1, z2,..., zn 是 ys 中的元素。
也就是说,grad_ys 中的每个张量会分别与对应的
ys 元素相乘,然后在计算相对于 xs
的梯度时,这些加权后的结果会参与到链式法则的计算中。
例如,在代码示例中:
1 | import tensorflow as tf |
如果不考虑 grad_ys,输出应该是:
1 | (array((3., 3., 3.), dtype=float32), |
现在在权重参数
grad_ys = ((-2.0,-3.0,-4.0), (-2.0,-3.0,-4.0))
的加权下,输出实际为:
1 | (array((-6., -9., -12.), dtype=float32), |
具体计算过程为,对于 w1 的梯度,原来的梯度是
3(来自 z1 对 w1
的偏导),现在加权后为 -2.0 * 3 = -6.0;对于
w2 的梯度,原来的梯度是 2(来自
z1 对 w2 的偏导),加权后为
-3.0 * 2 = -6.0;对于 w3 的梯度,来自
z1 的部分为 -2.0 * 1 = -2.0,来自
z2 的部分为 -2.0 * (-1) = 2.0,相加得到
0.0。
这样,通过设置 grad_ys,可以对 ys
中每个元素的梯度进行不同的加权,从而更灵活地控制梯度的计算。在实际应用中,这可以根据具体的需求和模型架构来调整梯度的传播和计算方式。
为什么需要加权
在某些情况下,需要对梯度进行加权是为了在计算梯度时对不同的部分进行不同程度的强调或重视。
例如,在深度学习中,不同的输出或误差项可能对最终的结果有不同的重要性。通过为
grad_ys中的每个张量设置合适的权重,可以根据这些重要性的差异来调整梯度的计算。
具体来说,加权可以用于以下几种情况:
- 强调重要的输出或误差:如果某些输出或误差对于模型的性能或目标更关键,那么可以给它们的梯度分配较大的权重,以便在反向传播过程中更显著地影响参数的调整。
- 平衡不同规模或量级的因素:当不同的输出或误差具有不同的量级时,加权可以帮助平衡它们对梯度的贡献,避免较大量级的部分主导了梯度的计算。
- 实现特定的优化目标:根据具体的优化目标或任务需求,设置特定的权重来引导模型的学习方向。
- 处理多任务学习:在多任务学习场景中,不同的任务可能具有不同的重要性,通过加权梯度可以更好地协调不同任务之间的学习。
例如,假设有两个输出 y1和
y2,对应的梯度分别为 dy1/dx和
dy2/dx。如果直接计算梯度之和,那么它们对最终梯度的贡献是相等的。但如果
y1相对更重要,就可以为
dy1/dx设置较大的权重,使得它在决定参数调整时起到更大的作用。
在 TensorFlow 中,通过设置
grad_ys参数来实现加权梯度计算。grad_ys是一个与
ys长度相同的张量列表,其中每个张量用于对相应的
ys元素的梯度进行加权。这样,在计算梯度时,就会考虑这些加权值,从而实现对不同部分梯度的不同程度的重视。
例如,在上述代码示例中:
1 | grad_ys = (tf.variable(((1))), tf.variable(((2)))) |
这里 grad_ys被设置为
(tf.variable(((1))), tf.variable(((2)))),表示在计算梯度时,res2a的梯度将乘以
1,而 res2b的梯度将乘以 2,从而实现了对
res2b的梯度相对更重视的效果。这样,在后续的反向传播和参数更新中,res2b的梯度将对参数调整产生更大的影响。
总的来说,加权梯度提供了一种灵活的方式,根据具体问题和需求,对不同部分的梯度进行定制化的处理,以更好地实现模型的学习和优化目标。但确定合适的权重通常需要对问题有深入的理解,并可能需要通过试验和调优来找到最优的设置。
如何为
grad_ys 中的每个张量设置合适的权重?
为
grad_ys中的每个张量设置合适的权重,需要根据具体的问题和模型需求来决定。设置权重的目的是为了在计算梯度时对不同的部分进行不同程度的加权。
一种常见的方法是根据对每个元素的重要性或关注度来分配权重。例如,如果某个元素对于最终结果的影响较大,或者你希望在梯度计算中更强调该元素的变化,那么可以为其分配较大的权重;反之,如果某个元素相对不那么重要,可以分配较小的权重。
另外,也可以基于一些先验知识或经验来设置权重。例如,在某些情况下,可能知道某些部分的梯度对于整体优化的重要性程度。
然而,确定最合适的权重通常需要通过试验和调优来找到。这可能涉及尝试不同的权重组合,并观察模型在训练或优化过程中的性能表现,以找到能够达到最佳效果的权重设置。
例如,在上述代码示例中:
1 | grad_ys = (tf.variable(((1))), tf.variable(((2)))) |
这里 grad_ys被设置为
(tf.variable(((1))), tf.variable(((2)))),表示在计算梯度时,res2a的梯度将乘以
1,而 res2b的梯度将乘以
2,从而实现了对不同部分梯度的不同加权。
具体到你的问题中,如何设置权重取决于你的具体任务和数据特点。你可能需要对问题有深入的理解,并结合一些实验和观察来找到合适的权重设置。这可能需要一些尝试和错误,以及对模型输出和性能的仔细分析。同时,也可以考虑使用一些自动调参的技术或算法来帮助找到最优的权重配置。
np.hstack
np.hstack 是 NumPy
库中的一个函数,用于水平(按列)堆叠数组。
其函数签名通常为 np.hstack(tup) ,其中 tup
是一个元组,包含要堆叠的数组。
例如,如果有两个数组 a = np.array([1, 2, 3]) 和
b = np.array([4, 5, 6]) ,使用
np.hstack((a, b)) 将会得到一个新的数组
[1, 2, 3, 4, 5, 6] 。
再比如,如果 a = np.array([[1, 2], [3, 4]])
,b = np.array([[5, 6], [7, 8]]) ,那么
np.hstack((a, b)) 的结果是
[[1, 2, 5, 6], [3, 4, 7, 8]] 。
np.hstack
主要用于将多个数组在水平方向上拼接成一个新的数组,前提是参与拼接的数组在除了要拼接的维度(这里是列维度)之外的其他维度上形状要匹配。
td error
TD error 即时间差分误差(Temporal Difference error),它是强化学习中一个重要的概念,用于衡量当前估计值与目标值之间的差异。
其定义为:当前时刻的状态值或动作值的估计与基于即时回报和下一时刻状态值或动作值的估计所构成的目标值之间的差值。
例如,在某个时刻 t,TD error 可以表示为:\(\delta_t = V_t(s_t) - (r_{t+1} + \gamma V_t(s_{t+1}))\) 或者 \(\delta_t = Q_t(s_t, a_t) - (r_{t+1} + \gamma Q_t(s_{t+1}, a_{t+1}))\) ,其中 \(V_t(s_t)\) 表示 t 时刻对状态 \(s_t\) 的状态值估计,\(Q_t(s_t, a_t)\) 表示 t 时刻对状态 \(s_t\) 采取动作 \(a_t\) 的动作值估计,\(r_{t+1}\) 是即时回报,\(\gamma\) 是折扣系数,\(V_t(s_{t+1})\) 和 \(Q_t(s_{t+1}, a_{t+1})\) 分别是下一时刻的状态值估计和动作值估计。
TD error 的主要作用是指导强化学习算法的学习和更新过程。通过计算 TD error,算法可以了解当前的估计与实际情况之间的差距,并据此调整模型的参数,以使得估计值更接近真实值。较小的 TD error 表示当前的估计较为准确,而较大的 TD error 则意味着模型需要进行更大的调整。
在强化学习中,一些算法(如 Q-learning、SARSA 等)会使用 TD error 来更新价值函数或策略,以逐步优化智能体的行为,使其能够在环境中获得更好的累积回报。
TD error 具有一些优点,例如它可以在没有完整状态序列的情况下进行学习,能够更快速灵活地更新状态或动作的价值估计。然而,它得到的价值是一种有偏估计,但其方差通常比其他方法(如蒙特卡洛方法)得到的方差要低。
不同的强化学习场景和算法中,TD error 的具体形式和应用可能会有所不同,但总体上都是用于衡量估计值与目标值的差异,以推动学习和优化的进行。如果在强化学习训练中遇到 TD error 值很大的情况,可能的原因包括网络架构不够复杂、训练样本数量不足、学习率过大或没有使用足够多的经验回放等。可以尝试使用更复杂的网络架构、增加训练数据、调低学习率、增加经验回放或使用更多的超参数调整方法来解决。
tf.distributions.Normal
tf.distributions.Normal 是 TensorFlow
中用于定义正态分布(高斯分布)的类。
它的初始化函数 __init__ 的参数如下:
loc:表示正态分布的均值(μ),是一个浮点型张量。scale:表示正态分布的标准差(σ),也是一个浮点型张量,且必须包含只正数值。validate_args:一个 Python 布尔值,默认为False。当为True时,会进行参数验证。allow_nan_stats:一个 Python 布尔值,默认为True,用于描述在统计量未定义时的行为。
通过创建 tf.distributions.Normal
对象,可以进行与正态分布相关的操作,例如采样、计算概率、计算熵、交叉熵、KL
散度等。例如:
1 | import tensorflow as tf |
在正态分布中,概率密度函数(pdf)的公式为:
\[ pdf(x; \mu, \sigma) = \frac{exp(-0.5(x - \mu)^2 / \sigma^2)}{\sqrt{(2\pi \sigma^2)}} \]
其中,loc = mu 是均值,scale = sigma
是标准差,z 是归一化常数。
正态分布是位置-尺度族的一员,也就是说,可以通过以下方式构建:
\[ x \sim Normal(loc=0, scale=1) \]
\[ y = loc + scale * x \]
tf.distributions.Normal 类中还提供了其他一些方法,如
covariance(协方差)、cross_entropy(交叉熵)、entropy(熵)、log_cdf(对数累积分布函数)、log_prob(对数概率)、log_survival_function(对数生存函数)、mean(均值)、mode(众数)、stddev(标准差)、variance(方差)等,这些方法可以方便地用于各种与正态分布相关的计算和操作。具体使用方法可以参考
TensorFlow 的官方文档。
这些方法使得在 TensorFlow
中处理正态分布变得更加方便和高效,尤其是在涉及到概率计算、随机采样以及与其他分布进行比较和组合的任务中。例如,在一些机器学习和深度学习模型中,可能需要使用正态分布来初始化参数、生成随机噪声或者构建概率模型等。通过
tf.distributions.Normal 类,可以以一种与 TensorFlow
计算图兼容的方式进行这些操作,从而更好地利用 TensorFlow
的自动微分和优化功能。同时,还可以方便地处理批量数据(即同时处理多个正态分布,每个分布具有不同的参数),这在处理大规模数据或多任务学习等场景中非常有用。
tf.clip_by_value
tf.clip_by_value是 TensorFlow
中的一个函数,用于将张量中的数值限制在指定的范围内。
它的语法如下:
1 | tf.clip_by_value(t, clip_value_min, clip_value_max, name=None) |
其中:
t:要进行裁剪的张量。clip_value_min:裁剪的最小值。如果张量中的值小于这个最小值,它们将被设置为这个最小值。clip_value_max:裁剪的最大值。如果张量中的值大于这个最大值,它们将被设置为这个最大值。name(可选):操作的名称。
例如,如果有一个张量 t,使用
tf.clip_by_value可以将其值限制在 2和
5之间:
1 | import tensorflow as tf |
输出结果将是:
1 | ((2.5, 2.5, 3.0), (4.0, 4.5, 4.5)) |
在上述例子中,原始张量 t中的值小于
2.5的被替换为 2.5,大于
4.5的被替换为 4.5。
需要注意的是,clip_value_min需要小于或等于
clip_value_max,以获得正确的结果。如果输入的张量
t的元素类型是整数,而 clip_value_min或
clip_value_max是浮点数,需要先将整数张量转换为浮点数,否则可能会引发类型错误。此外,clip_value_min和
clip_value_max可以是标量张量,也可以是能广播到张量
t形状的张量。
torch.nn.Module
torch.nn.Module 是 PyTorch
中所有神经网络模块的基类。它提供了许多用于构建和训练神经网络的基本功能。以下是一些关键点:
模型定义:
torch.nn.Module是所有神经网络模块的基类,因此你可以通过继承它来定义自己的神经网络模型。例如:1
2
3
4
5
6
7
8
9
10import torch.nn as nn
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.fc = nn.Linear(10, 1) # 定义一个全连接层
def forward(self, x):
x = self.fc(x)
return x参数管理:
torch.nn.Module自动管理模型的所有参数。当你定义一个神经网络层(如nn.Linear、nn.Conv2d等)时,这些层会自动添加到模型的参数列表中。例如,在上面的MyModel中,self.fc是一个线性层,它的参数(权重和偏置)会被自动添加到模型中。前向传播:你需要定义一个
forward方法来指定数据如何通过模型进行前向传播。例如,在上面的MyModel中,forward方法将输入x传递给线性层self.fc。训练和评估:
torch.nn.Module提供了一些方法来管理模型的训练和评估过程,例如train()、eval()、zero_grad()、step()等。保存和加载:
torch.nn.Module提供了save和load_state_dict方法来保存和加载模型的参数。例如:1
2
3model = MyModel()
torch.save(model.state_dict(), 'model.pth')
model.load_state_dict(torch.load('model.pth'))子模块:
torch.nn.Module可以包含其他子模块,这些子模块也可以是torch.nn.Module的实例。例如,一个复杂的神经网络可能由多个层和子网络组成。
总的来说,torch.nn.Module 是 PyTorch
中构建和训练神经网络的核心类,它提供了许多方便的功能来管理模型参数、前向传播、训练和评估等。
abc.ABC
#abc.ABC 是 Python 的抽象基类,用于定义抽象方法。
在 Python 中,abc.ABC类是用于实现抽象基类(Abstract Base
Class)的。
抽象基类主要用于定义一组必须由其子类实现的方法。通过从
abc.ABC类继承,您可以创建一个抽象基类,并在其中定义抽象方法。
例如:
1 | import abc |
在上述示例中,MyAbstractClass是一个抽象基类,它定义了一个抽象方法
abstract_method。ConcreteClass是
MyAbstractClass的子类,并且实现了这个抽象方法。
使用抽象基类的好处在于,它可以强制子类遵循一定的接口规范,有助于提高代码的可读性、可维护性和可扩展性。例如,在一个大型项目中,如果多个类都需要实现某些特定的方法,通过定义一个抽象基类,可以确保这些方法在所有相关的子类中都得到正确实现。
@property
@property 是 Python
的装饰器语法,用于将一个方法转换为只读属性。这意味着你可以像访问属性一样访问这个方法,而不需要调用它。这对于创建只读属性或需要计算属性值的方法非常有用。
下面是一个简单的例子:
1 | class Circle: |
在这个例子中,radius 和 diameter
都是只读属性。radius 属性直接返回 _radius
属性的值,而 diameter 属性计算并返回直径的值。
使用 @property
装饰器的好处是,它允许你保持属性访问的一致性,同时提供额外的功能。例如,你可以使用
@property 装饰器来定义一个计算属性,或者使用
@property 和 @radius.setter
装饰器来定义一个可写的属性。
import gym
import gym 通常用于导入 OpenAI Gym 库。
OpenAI Gym 是一个用于开发和比较强化学习算法的工具包。它提供了各种各样的环境,例如经典控制问题(如 CartPole、MountainCar 等)、Atari 游戏等。
通过导入 Gym 库,您可以创建这些环境,并与它们进行交互,以测试和开发强化学习算法。
例如:
1 | import gym |
在上述代码中,首先创建了 CartPole-v1
环境,然后进行了一系列的交互操作,包括获取初始观察值、采取动作、获取新的观察值和奖励等。
不同的环境具有不同的状态、动作空间和奖励机制,您可以根据具体的问题和需求选择合适的环境进行强化学习算法的开发和实验。
torch.utils.data.DataLoader
torch.utils.data.DataLoader是 PyTorch
中用于加载数据的重要工具。以下是关于它的详细介绍:
一、功能概述
DataLoader的主要作用是将数据集(通常是自定义的数据集类对象)进行封装,为模型训练或评估提供高效的数据迭代器。它可以自动处理数据的批处理、随机打乱、并行加载等操作,极大地简化了数据加载的过程。
二、主要参数
dataset:这是必须提供的参数,代表要加载的数据集对象。这个数据集对象通常需要实现__len__方法以返回数据集的大小,以及__getitem__方法以支持通过索引获取数据样本。batch_size:指定每一批数据的大小。例如,如果设置为 32,那么每次迭代将返回 32 个数据样本。shuffle:布尔值,表示是否在每个 epoch 开始时随机打乱数据的顺序。对于训练集,通常设置为 True 以增加数据的多样性;对于测试集,一般设置为 False。num_workers:指定用于数据加载的子进程数量。增加这个值可以提高数据加载的速度,但也会占用更多的系统资源。collate_fn:一个可选的函数,用于将一批数据样本整理成适合模型输入的格式。如果不提供,DataLoader会使用默认的整理函数。pin_memory参数主要用于提高数据从 CPU 内存传输到 GPU 内存的速度。当pin_memory=True时,DataLoader会在将数据加载到 CPU 内存后,立即将其复制到一个固定的(pinned)内存区域。这个固定内存区域可以被直接映射到 GPU 的内存地址空间,从而减少了数据从 CPU 传输到 GPU 时的内存复制开销。
三、使用方法
- 首先,定义一个自定义的数据集类,实现
__len__和__getitem__方法。例如:
1 | from torch.utils.data import Dataset |
- 然后,创建
DataLoader对象:
1 | import torch |
- 最后,可以通过迭代
DataLoader对象来获取批量数据:
1 | for batch in dataloader: |
四、优势和应用场景
- 高效的数据加载:通过并行加载和批处理,可以大大提高数据加载的速度,减少模型训练或评估的等待时间。
- 灵活性:可以与各种不同类型的数据集配合使用,包括自定义的数据集类。同时,可以方便地调整批处理大小、随机打乱等参数,以适应不同的任务需求。
- 深度学习中的广泛应用:在图像分类、自然语言处理、语音识别等深度学习任务中,
DataLoader是不可或缺的工具,用于为模型提供训练和测试数据。
np.clip
“np.clip”通常是在 Python 编程中使用的一个函数。它用于将数组中的值限制在给定的区间范围内,以达到对数值进行裁剪或限制的目的。
图解nn.Conv1d的具体计算过程
以下图解了1维卷积的计算过程,特别注意输入、卷积核参数、输出 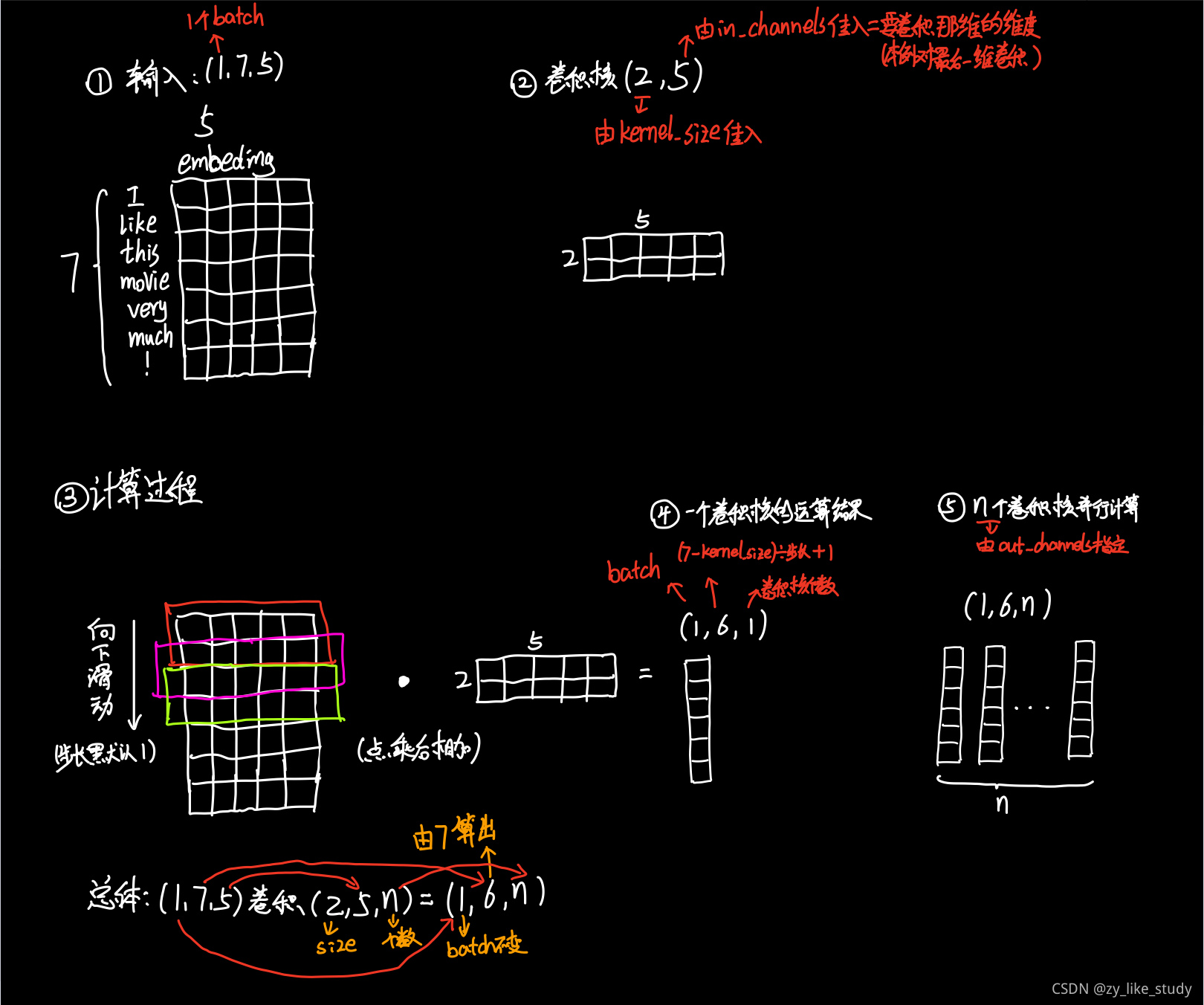
代码实现:注意pytorch中只能对倒数第1维数据进行卷积,因此传参时要转置一下,将需要卷积的数据弄到倒数第1维,这里将embeding的维度进行卷积,最后一般会在转置过来(没办法,pytorch设计的不太好,这点确实绕了一圈)--------(技巧就是把将需要卷积的数据弄到倒数第1维)
1
2
3
4
5# [1,7,5] 卷积 [2,5,3] = [1, 6, 3]
a = torch.ones(1,7,5)
b = nn.Conv1d(in_channels=5, out_channels=3, kernel_size=2)(a.permute(0,2,1))
b = b.permute(0,2,1)#再换过来
输出结果: tensor([[ [ 0.2780, 0.6589, -0.5446], [ 0.2780, 0.6589, -0.5446], [ 0.2780, 0.6589, -0.5446], [ 0.2780, 0.6589, -0.5446], [ 0.2780, 0.6589, -0.5446], [ 0.2780, 0.6589, -0.5446]]]) torch.Size([1, 6, 3])
Padding 参数:
在PyTorch中,\(nn.Conv1d\)的 \(padding\)参数用于指定在输入张量的每个维度上添加的零填充的数量。具体来说,\(padding\)参数可以控制卷积操作后输出张量的尺寸。
假设输入张量的形状为 \((N, C_{in}, L_{in})\),其中 \(N\)是批次大小,\(C_{in}\)是输入通道数,\(L_{in}\)是输入序列长度。卷积核的大小为 \(K\),步幅为 \(S\),\(padding\)参数为 \(P\),那么输出张量的序列长度 \(L_{out}\)可以通过以下公式计算:
1 | L_{out} = (L_{in} + 2P - K) / S + 1 |
如果 \(L_{out}\)不是整数,那么 \(nn.Conv1d\)会抛出一个错误,因为输出张量的尺寸必须是整数。
以下是一个示例:
1 | import torch.nn as nn |
在这个示例中,\(padding=1\)表示在输入张量的每个维度上添加一个零填充。因此,如果输入张量的形状为 \((N, 16, L_{in})\),那么输出张量的形状为 \((N, 33, L_{out})\),其中 \(L_{out}\)是通过上述公式计算得到的。
注意,\(padding\)参数只影响输出张量的尺寸,不影响输入张量的尺寸。如果你想要改变输入张量的尺寸,可以使用
nn.ZeroPad1d或其他填充方法。
为什么在设置 model.eval() 之后,pytorch模型的性能会很差?
我使用pytorch构建使用 BatchNormalization 层的分割模型。我发现在测试中设置 model.eval() 时,测试分割结果为0。如果不设置 model.eval() ,它将运行良好。我试图搜索相关问题,但得出的结论是 model.eval() 可以固定BN的参数,但是我仍然对如何解决此问题感到困惑。我的batchsize设置为1,是否有此影响呢?
优化器:
参考此问题下面的12个答案及我的实验结果,给出修改代码的总结,请按排序进行:
如果batch_szie为1,增加bacth_size,建议值为8;(也可参考你领域内论文的batch_size大小,但不要设置为1)(batch_size太小,会导致bn层求到的标准差和总体数据差别较大,理论上可以接受。 但是,我尝试使用一个数据(一个点云)过拟合实验,train和eval的数据输入完全一样,batch_size为1。train模式下,网络的输出结果非常完美,但在eval模式的结果会 直接崩掉 ,可以说是完全没有效果。增加数据集到51个数据,batch_size增加到8,网络在train和eval模式的性能相同。)
代码错误:重复调用了同一个bn层。(定义一层bn层并多次调用,就会导致eval后性能崩溃.假设有两层feature A和B在训练阶段通过了norm层,A的均值方差为(1, 0) B的均值方差为(-1, 0),那么在train()的时候,由于前向传播中的norm都是使用的batch计算出来的均值方差,因此不会影响,但是,norm层会统计下前向传播中通过的feature的总的均值方差(类似于滑动平均的算法)使得可以在测试也就是eval ()的时候,可以对单个样本进行测试,那既然A B 都在训练阶段通过了,该norm层中记录的滑动平均后的均值方差可能是(0, 0)这个样子(也就是A和B的平均),在eval()的时候就完蛋了,因为这个记录的方差均值和A B都对不上,模型直接崩溃。所以总结下来本质原因就是,训练阶段,norm用的是一批数据自身的均值方差,测试阶段,norm用的是记录的均值方差,但是如果多个不同的feature通过该层norm,就会导致记录的均值方差不准确)
如果代码中同时使用了dropout和bn层,删除其中一类网络层。(参考论文《Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift》,简单来说就是因为dropout从训练模式切换到测试模式的时候会对特定的神经元引入方差偏移,但是bn层在测试阶段会始终使用它在训练阶段统计到的方差,方差的不一致导致了测试阶段的错误预测。
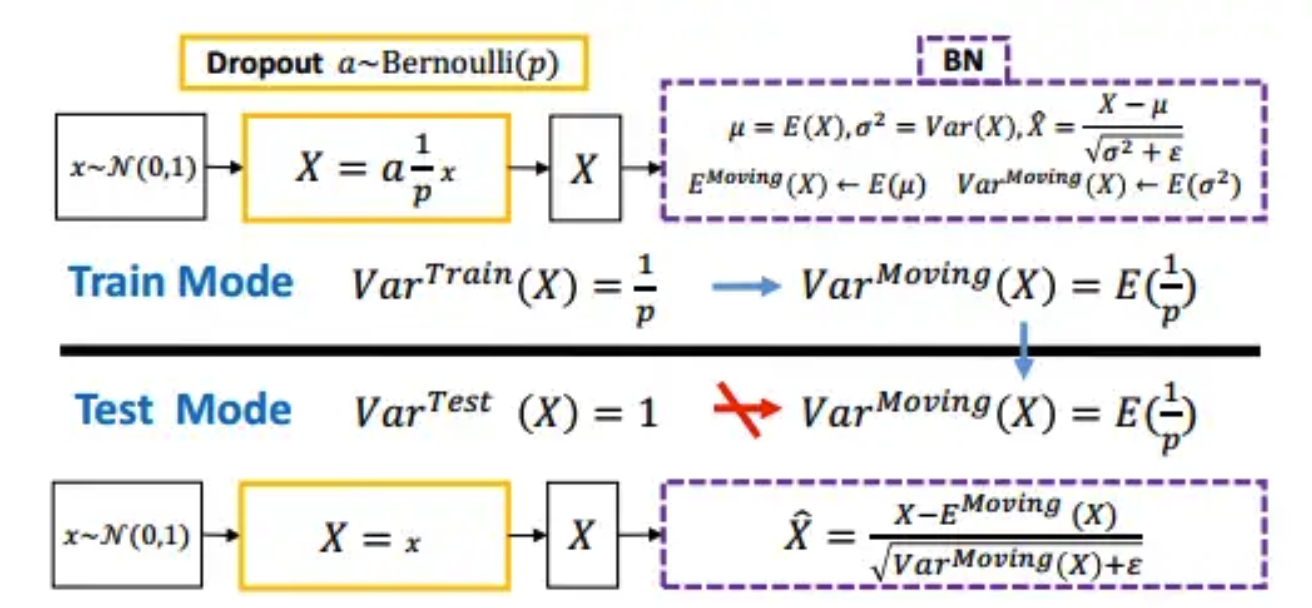
但是也有人说实验中其实只要不是drop后面立马跟bn就没太大问题(比如conv-bn-relu-dropout-pool?) 那些理论分析看看就好,实际参考价值有限。也有人说卷积核用dropout效果会更差,dropout更适用于fc层,有研究表明。语义分割的代码里很少看到dropout)
输入数据做归一化。
其实dropout已经默认做了额外处理: 在测试(或验证)阶段,Dropout层的行为与训练阶段不同。Dropout是一种正则化技术,它在训练过程中随机地丢弃(设置为0)神经网络中的一部分神经元,以防止过拟合。在训练时,Dropout层会按照设定的概率(通常称为p)随机地将一些神经元的输出设置为0,而其他神经元的输出则保持不变,但会被放大,以保持输出的期望值与没有Dropout时相同。
然而,在测试阶段,我们通常希望模型能够使用所有的神经元来做出预测,因此不需要进行随机丢弃操作。为了确保在测试时模型的输出与训练时的期望输出一致,需要进行以下操作:
关闭Dropout:在测试阶段,应该关闭Dropout,即不进行随机丢弃操作。这通常通过设置Dropout层的train()方法为False来实现,或者在创建Dropout层时设置train=False。
缩放输出:在训练时,由于随机丢弃了一部分神经元,其他神经元的输出会被放大。为了在测试时保持输出的期望值与训练时一致,需要将所有神经元的输出按Dropout概率的倒数进行缩放。例如,如果Dropout概率p为0.5,那么在测试时,每个神经元的输出应该乘以2(即1/p)。
在PyTorch中,Dropout层会自动处理这种缩放操作。当你在测试阶段使用Dropout层时,PyTorch会自动关闭Dropout并进行必要的输出缩放。因此,你不需要手动进行这些操作,只需确保在测试阶段不启用梯度计算,并且正确地使用Dropout层即可。
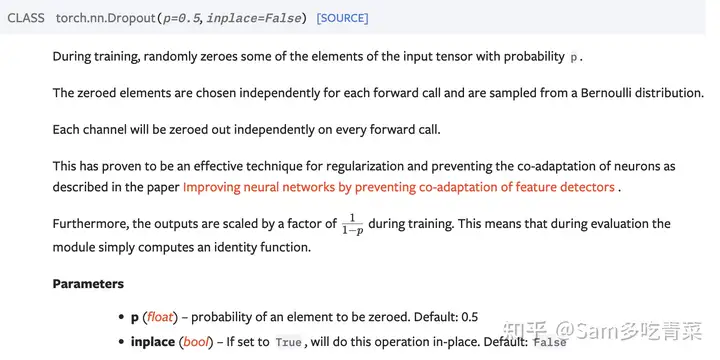
BatchNorm测试时统计量怎么来
Batch Normalization训练时,使用的均值和方差统计量是从同batch数据的同一特征维度统计而来。
而测试时,为了保证每个测试点的预测输出不受batch内其他数据影响,肯定得采用固定的统计量,这个统计量从何而来呢?
直观的想法是再过一遍整个训练集,在整个训练集上估计均值和方差,但在数据多的时候,每次在测试之前都要过一遍整个训练集超级费时:
因此,我们需要一个近似的在训练时估计全局统计量分布的办法。这个统计量要满足两个要求:
- 尽量反映整个训练集的分布;
- 尽量使用模型训练结束或者即将结束时的权重来计算,以便和测试时行为一致。
考虑到这两个要求,是不是想起了SGD里的momentum?采用训练时指数滑动平均的方式就可以得到测试时用的统计量,参考torch的官方文档:

作为常用的防止过拟合的手段,Dropout 和 BN 都能起到比较好的结果,但不是在任意位置都奏效。我了解到的是,Dropout 通常在 FC 层有效,而在卷积层就不推荐用了。至于 BN,至少我用在卷积层是 ok 的。
model.eval()影响大模型吗
我们已经厘清了model.eval()对dropout层和batch norm层的影响,那么model.eval()影响大模型吗这个问题就等价于:大模型用batch norm和dropout吗?
首先,大模型用的都是layer norm, batch norm显然是不存在的。那么大模型开dropout吗?
先明确一下dropout的位置,大多数transformer的实现(尤其是类gpt的decoder模型中)只在self-attention的softmax概率之后使用dropout,相应的失活概率p为超参数attention_dropout。
而在LLaMA、Mistral这些常见的开源大模型中,attention_dropout都被设为0,也就是实际上不使用dropout,model.eval()对这些不开dropout的大模型实际上没有影响。
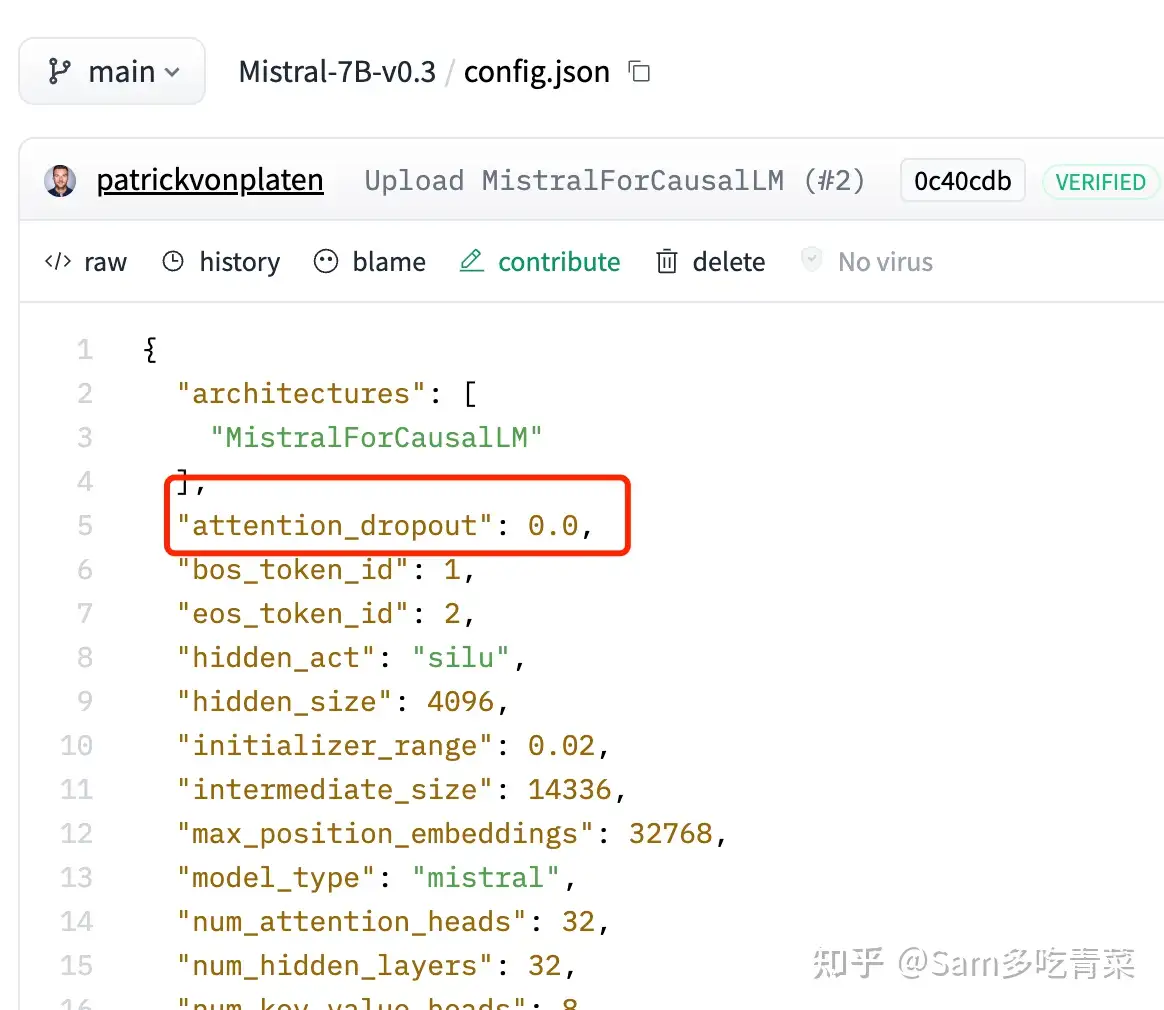
RMSprop优化器
RMSprop是一种自适应学习率优化算法,特别适用于处理非平稳目标函数。下面是对代码的详细解释:
cfg.TRAIN.OPTIMIZER == 'rmsprop': optimizer = optim.RMSprop( #model.parameters(), filter(lambda p: p.requires_grad, model.parameters()), lr=cfg.TRAIN.LR,#学习率 momentum=cfg.TRAIN.MOMENTUM,#动量 weight_decay=cfg.TRAIN.WD,#权重衰减 alpha=cfg.TRAIN.RMSPROP_ALPHA,#衰减率 centered=cfg.TRAIN.RMSPROP_CENTERED#是否使用中心化的RMSprop )
参数解释:
filter(lambda p: p.requires_grad, model.parameters()):这个参数用于选择需要更新的模型参数。filter函数会遍历模型的所有参数,并保留那些requires_grad属性为True的参数,即需要计算梯度的参数。 lr=cfg.TRAIN.LR:学习率,控制每次参数更新的步长。 momentum=cfg.TRAIN.MOMENTUM:动量,用于加速梯度下降并抑制震荡。 weight_decay=cfg.TRAIN.WD:权重衰减,也称为L2正则化,用于防止过拟合。 alpha=cfg.TRAIN.RMSPROP_ALPHA:RMSprop算法中的衰减率,用于调整梯度平方的指数衰减速度。 centered=cfg.TRAIN.RMSPROP_CENTERED:是否使用中心化的RMSprop。如果为True,则使用中心化的版本,否则使用非中心化的版本。
RMSprop是一种自适应学习率优化算法,它通过动态调整学习率来优化神经网络训练过程。下面是对这些参数的详细解释:
- 学习率(Learning Rate, lr): 学习率是控制每次参数更新的步长大小。较大的学习率可能导致训练过程不稳定,而过小的学习率则可能导致训练过程过慢。RMSprop通过动态调整学习率,使得模型在训练初期可以快速收敛,而在后期可以更精细地调整参数。
- 动量(Momentum): 动量是一种加速梯度下降并抑制震荡的技术。在每次更新参数时,不仅考虑当前梯度,还考虑之前梯度的累积信息。具体来说,动量项会使得参数更新方向更加稳定,从而加速收敛并减少震荡。
- 权重衰减(Weight Decay, wd): 权重衰减是一种正则化技术,用于防止过拟合。它通过在损失函数中添加一个与参数大小成正比的项来抑制参数的绝对值过大。权重衰减相当于在优化过程中施加了一个L2正则化项。
- 衰减率(Alpha): 衰减率是RMSprop算法中的一个超参数,用于控制梯度平方的指数衰减速度。较大的衰减率会使梯度平方的更新更加平滑,而较小的衰减率则会使更新更加敏感。
- 是否使用中心化的RMSprop: 中心化的RMSprop是在计算梯度平方的均值时,同时考虑梯度的均值。中心化的RMSprop在处理稀疏梯度时表现更好,因为它可以更好地处理梯度中的噪声。
总结来说,这些参数共同作用,使得RMSprop优化器能够自适应地调整学习率,加速训练过程,并防止过拟合。在实际应用中,需要根据具体任务和数据集来调整这些参数,以达到最佳的训练效果。
设置更新学习率的轮次
lr_scheduler = torch.optim.lr_scheduler.MultiStepLR( optimizer, config.TRAIN.LR_STEP, config.TRAIN.LR_FACTOR, last_epoch-1 )
torch.optim.lr_scheduler.MultiStepLR:
- 这是PyTorch中的一个学习率调度器类,用于在训练过程中按设定的步长(epoch)调整学习率。
optimizer:
- 这是优化器对象,通常是一个
torch.optim.Optimizer的实例,例如torch.optim.SGD或torch.optim.Adam。优化器负责更新模型参数。
config.TRAIN.LR_STEP:
- 这是一个列表,包含了学习率需要调整的epoch索引。例如,如果
config.TRAIN.LR_STEP = [30, 60],那么学习率会在训练的第30和第60个epoch时调整。
config.TRAIN.LR_FACTOR:
- 这是一个列表,包含了对应步长时学习率调整的因子。例如,如果
config.TRAIN.LR_FACTOR = [0.1, 0.01],那么在第30个epoch时学习率会乘以0.1,在第60个epoch时学习率会再乘以0.01。
last_epoch-1:
last_epoch是最后一个epoch的索引,通常在继续训练时使用。last_epoch-1是为了确保在继续训练时,学习率调度器从正确的epoch开始调整。
Lipschitz连续 利普希茨约束
用于理解上面 BatchNorm 的原理补充
https://zhuanlan.zhihu.com/p/520107941
 https://kexue.fm/archives/6992
https://kexue.fm/archives/6992




L2 正则化能使得模型更好地满足 L 约束



采样分布

模型参数的初始化
https://kexue.fm/archives/7180

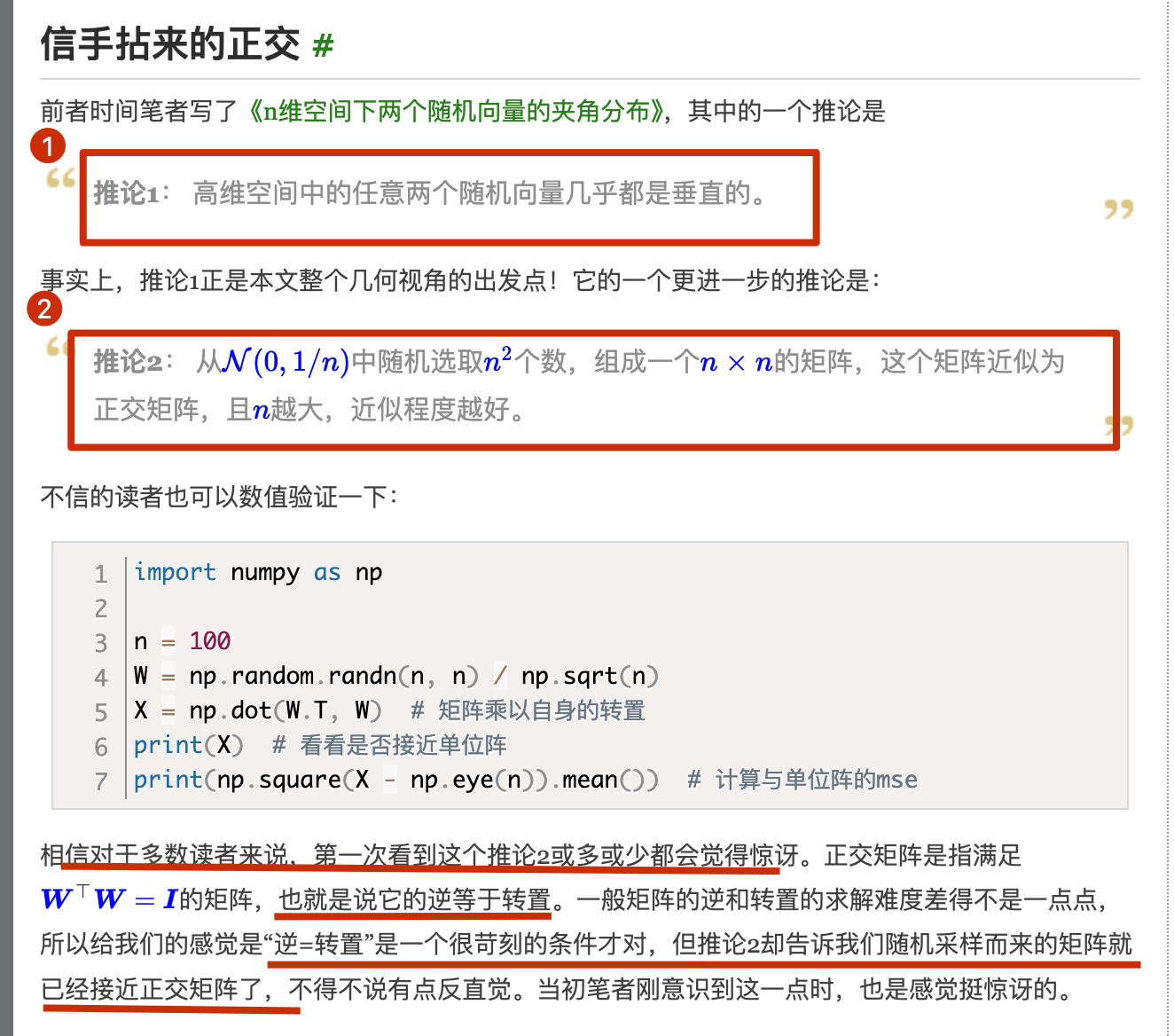
推导过程(可以跳过)


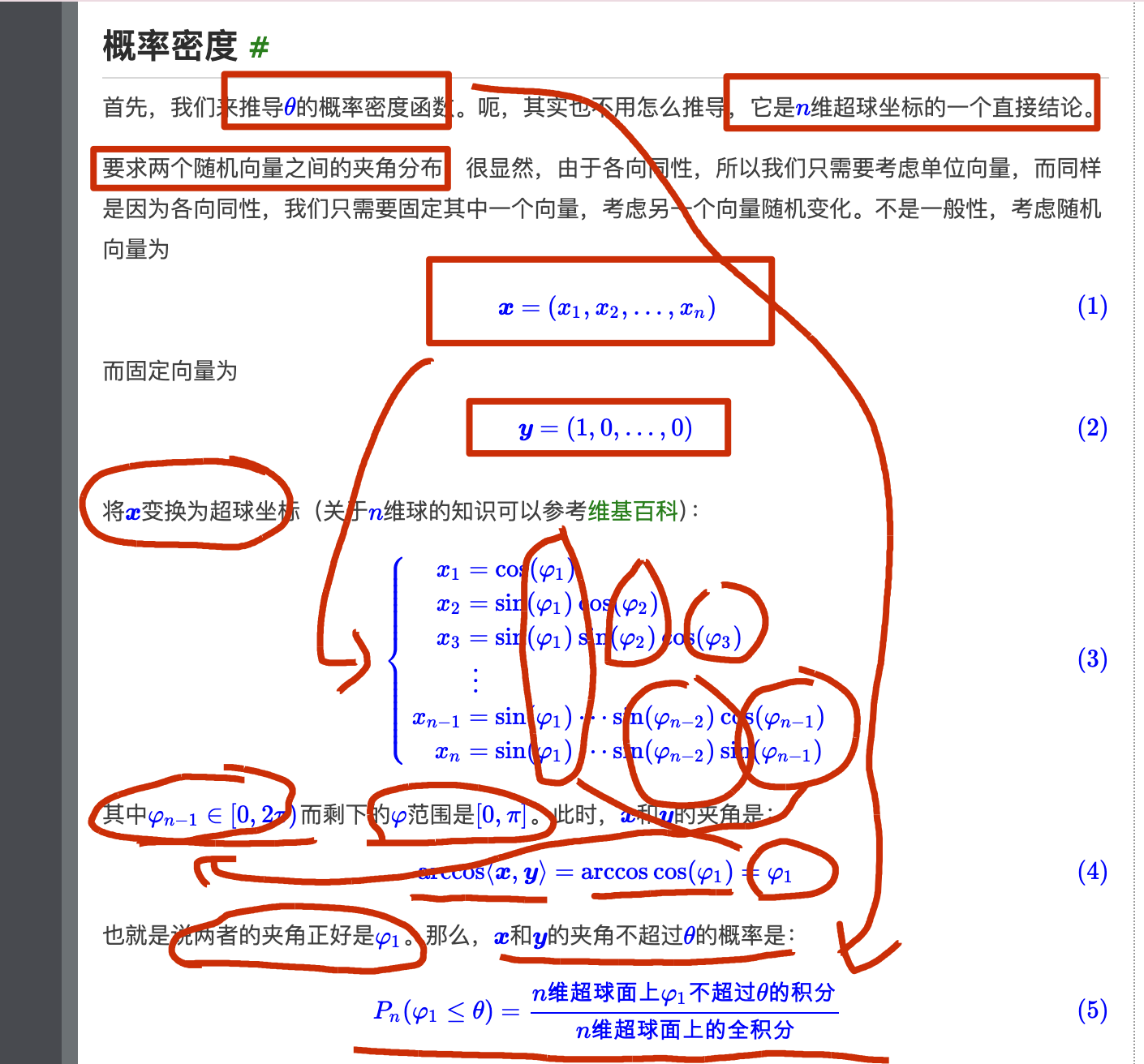
不对啊,x1 按上面的公式应该属于 0-1,但是显然不对啊,我估计他是 r 设置为 1 了,x 是球面上的点
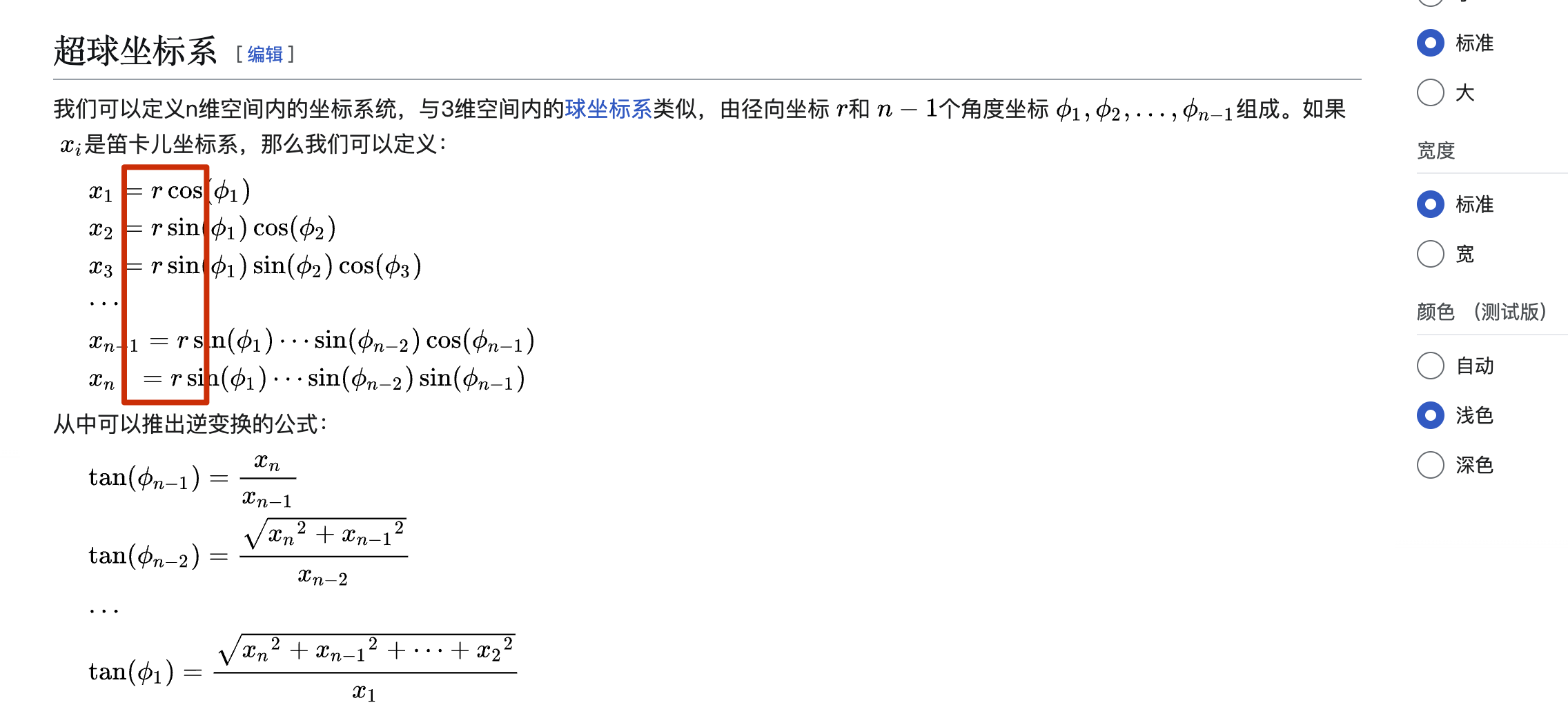



注: 上面是固定了一个向量 y,随机取x,当 n 越来越大时,x 与 y几乎都是垂直的
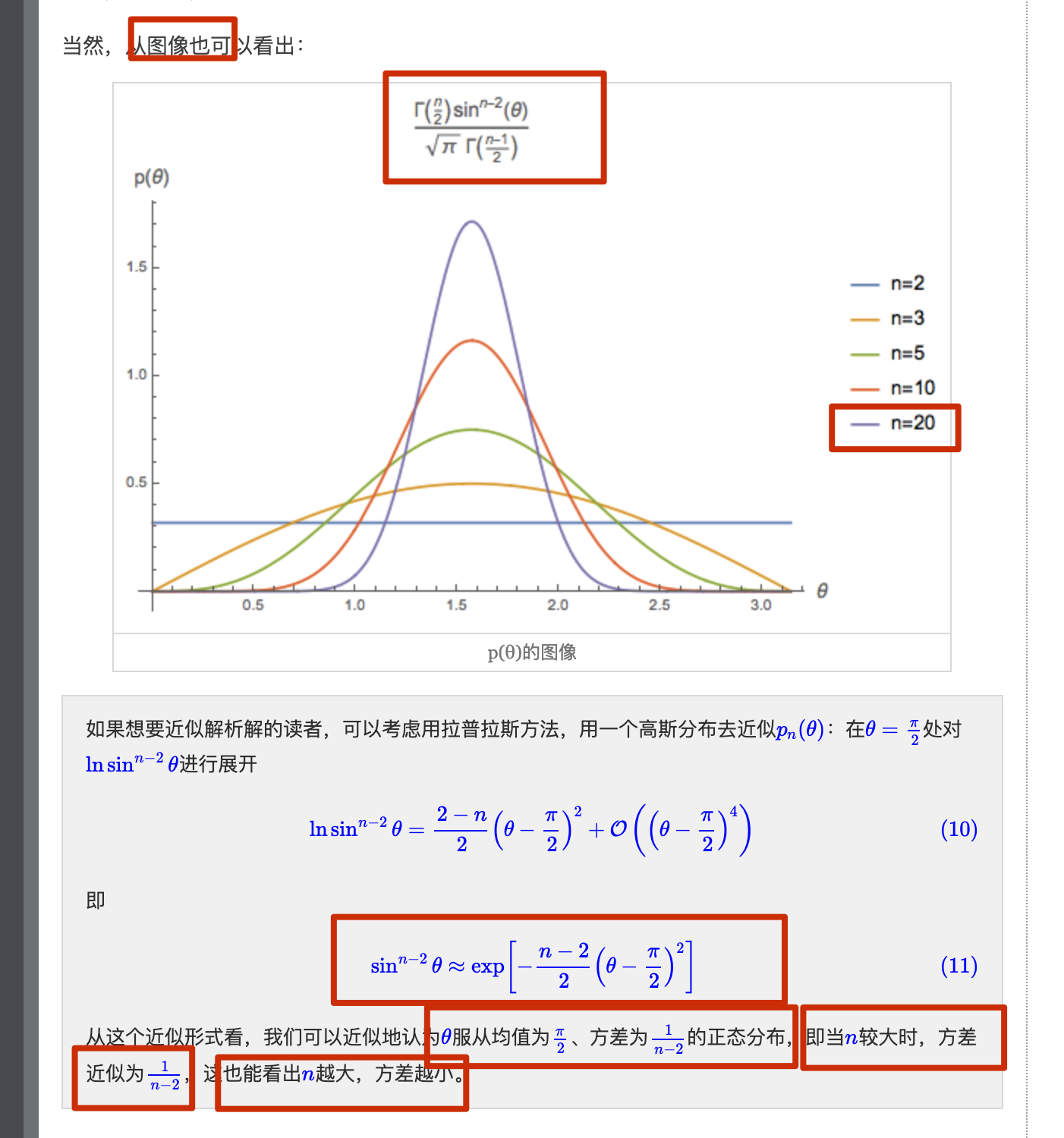
继续说明模型参数的初始化策略
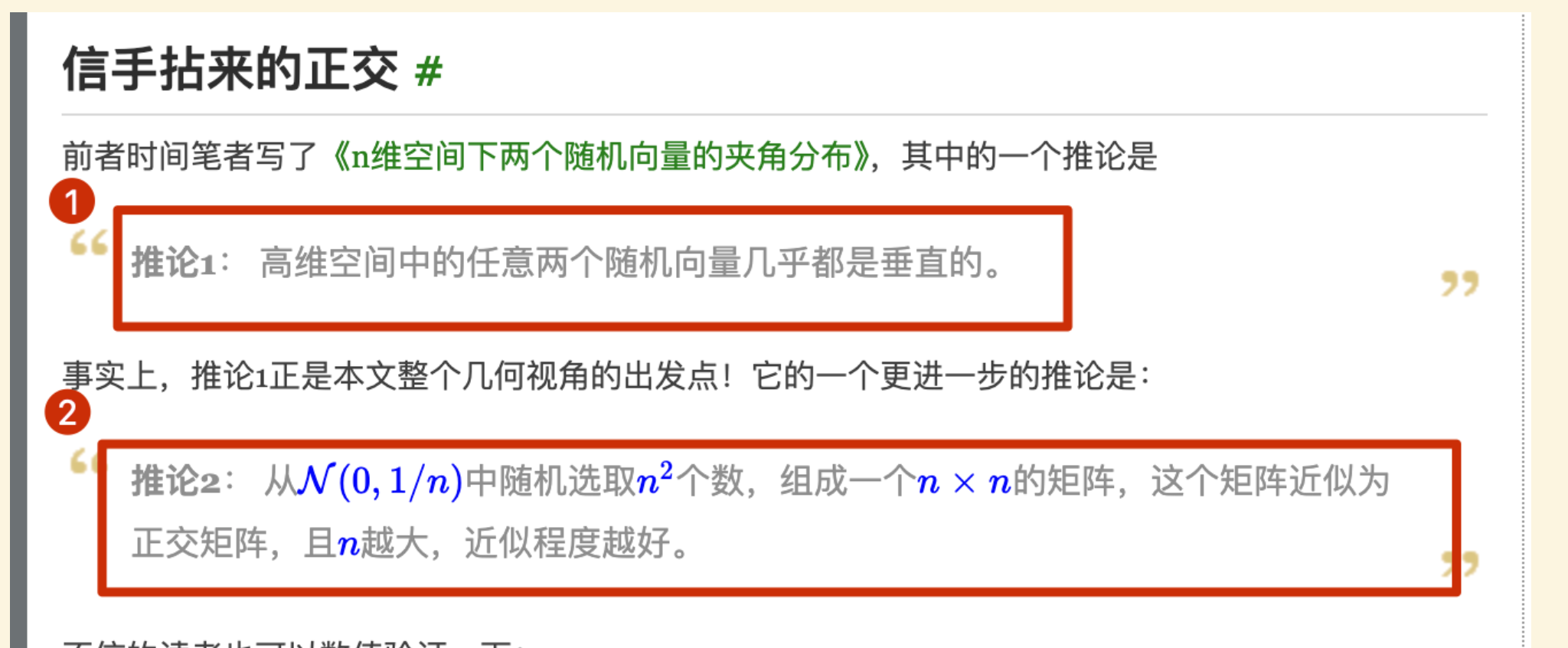


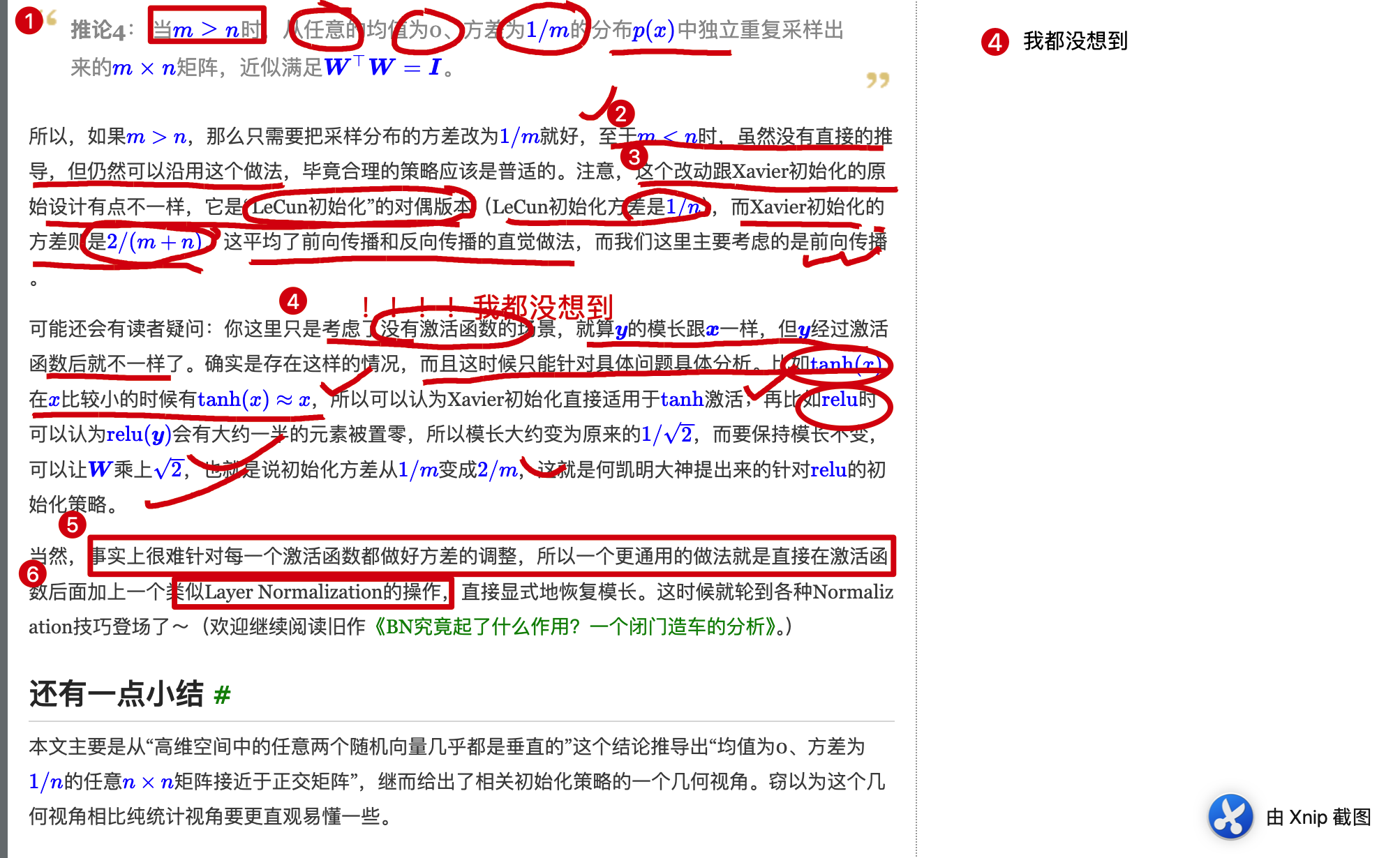

激活函数
selu就是对 elu 的微调

直接标准化
RMS Norm


一个直观的猜测是,center操作,类似于全连接层的bias项,储存到的是关于预训练任务的一种先验分布信息,而把这种先验分布信息直接储存在模型中,反而可能会导致模型的迁移能力下降。所以T5不仅去掉了Layer Normalization的center操作,它把每一层的bias项也都去掉了。
NTK参数化


残差连接



